Aucun titre de diapositive
Distance entre 2 plans voisins. = grandeur constante = distance interréticulaire dhkl. dhkl. (001). P1. P2. P3. P4. Plan réticulaire (h k ) : plan passant
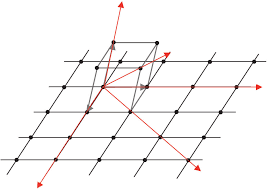Réseaux cristallins et symétrie dorientation dans les cristaux
26 déc. 2013 Plans cristallins (ou plans réticulaires) ... Trois nœuds non situés sur une même rangée définissent un plan cristallin. (ou plan réticulaire).
Diapositive 1
Calculer les distances inter-réticulaires des familles (001) (011) et. (111) dans les modes P
Module : Structure de la Matiére
* On définit une famille de plans réticulaires par les indices de Miller (hk
COURS DE CRISTALLOGRAPHIE
Le chapitre 2 est consacré aux calculs dans les réseaux : métrique d'un réseau produit scalaire
polycopié Cristallographie.pdf
Le premier chapitre est consacré à des généralités et des notions de base comme la notion de la maille et de la structure cristalline les plans réticulaires et
Table des matières
1 mars 2019 ... plans donnée le plan réticulaire le plus proche de l'origine (voir fig. 1.42) coupe les axes de la maille en abc h' k' /'. (1.4.24) h
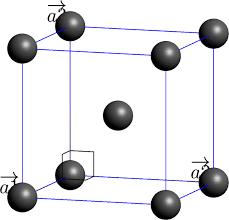Eléments de cristallographie
28 nov. 2016 ... pdf sans avoir besoin de l'aide d'un logiciel extérieur de ... Le plan réticulaire (hkl) intercepte la maille élémentaire en (1/h1 ...
Université dOran des Sciences et de la Technologie -Mohamed
Un plan réticulaire (plan cristallin) d'équation : h.x + k.y + l.z = m. ; m = (0 1
Diffraction des rayons X
Plans Réticulaires. ❑ Plan réticulaire: ❖ Plan passant par 3 nœuds non alignés. ❖ repéré par ses indices de Miller (hkl):. ➢ Un plan (hkl) coupe l'axe x en
Réseaux cristallins et symétrie dorientation dans les cristaux
30 déc. 2013 Un plan réticulaire contient une infinité de nœuds. ... Indices caractéristiques d'une famille de plans réticulaires.
Aucun titre de diapositive
Plan réticulaire (h k ) : plan passant par. 3 noeuds non alignés avec h k et entiers. 1ers entre eux = indices de Miller.
Cours de Cristallographie
Pour trouver rapidement les indices d'une famille de plans réticulaires à partir d'un plan il faut considérer : • qu'une famille de plans est définie par 3
Exercices de radiocristallographie Corrections
A) Placer un plan réticulaire dans une maille et calcul de distances réticulaires. Exercice 2a : Soit une maille orthorhombique ab
Travaux Pratiques Travaux Pratiques Matériaux Matériaux 1
Indices de Miller (Directions-rangées- et plans dans un cristal) : Un plan réticulaire (plan cristallin) d'équation : h.x + k.y + l.z = m ; m = (0 1
Université dOran des Sciences et de la Technologie -Mohamed
VI- Indices de Miller (directions-rangées- et plans dans un cristal)… Un plan réticulaire (plan cristallin) d'équation : h.x + k.y + l.z = m.
Eléments de cristallographie
figures d'être visualisées en 3 dimensions à l'intérieur du fichier pdf ... Dans chaque plan réticulaire les noeuds forment un réseau bidimensionnel.
COURS DE CRISTALLOGRAPHIE
Le chapitre 2 est consacré aux calculs dans les réseaux : métrique d'un réseau produit scalaire
LP339 – Cohésion de la matière – Cristallographie • Pour chacune
RANGEES - INDICES DE MILLER - PLANS EN ZONE. 2.1 réseau bidimensionnel. • il s'agit de retrouver les vecteurs directeurs des droites (AB) et (CD).
Diapositive 1
plans réticulaires et les réseaux de Bravais. Calculer les distances inter-réticulaires des familles (001) (011) et. (111) dans les modes P
Cristallographie : Notions de cristallochimie
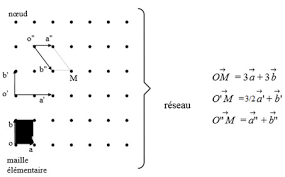
Les plans réticulaires sont caractérisés par les trois indices de Miller Soit un plan défini par ses trois intersections A B et C avec les axes x y et z respectivement les trois indices de Miller sont : OA OB OC 1 1 1 Ex Plan réticulaire d’indices : ? ? 1 2 1 1 c -à-d 0½0 b r
Qu'est-ce que le plan réticulaire?
Le plan réticulaire est un plan qui passe par des noeuds. Les indices de Miller (h, k, l ; entiers) caractérisent la position du plan dans l’espace. Un plan ( h k l ) découpe sur les axes les segments : OA=a/h, OB=b/k, OC=c/l Indices de Miller 111 110 010 101 ue Indices de Miller ue 111 222 100 123 Indices de Miller
Comment calculer l’équation d’un plan réticulaire?
Soit dans un réseau dont les vecteurs de base sont a, b, et c, l’équation du plan ABC s’écrit :h.x/a + k.y/b + l.z/c = 1 Indices de Miller Le plan réticulaire est un plan qui passe par des noeuds. Les indices de Miller (h, k, l ; entiers) caractérisent la position du plan dans l’espace. Un plan ( h k l ) découpe sur les axes les segments :
Quels sont les indices de la famille de plans réticulaires ?
Définition des indices h, k et l de la famille de plans réticulaires (hkl). et c. Toutefois (et en général) d’autres plans de la famille s’intercalent et découpent le vecteur a en h parties égales, le vecteur b en k parties égales et le vecteur c en l parties égales.
Comment calculer un plan réticulaire parallèle ?
Si le plan réticulaire est parallèle à un axe, le nombre de Miller correspondant est nul Réciproquement, si (h,k,l) sont trois nombres entiers relatifs quelconques, premiers entre eux dans leur ensemble et non tous nuls, ils définissent une famille de plans réticulaires parallèles d'équation hx+Ky+Lz= n
Eléments de cristallographie
Notes de cours, T. Auger, CentraleSupélec/MSSMAT (thierry.auger @ centralesupelec.fr)Table des matières
1 Réseau de Bravais . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22 Groupe de symétrie ponctuel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52.1 Symboles de Pearson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52.2 Groupe de symétrie ponctuel : définition . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62.3 Liste des groupes ponctuels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73 Espace direct . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
83.1 Indices de Miller . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93.2 Diffraction par une maille d"une onde plane et réseau réciproque . . . . . . . . . . . . .
103.3 Relation entre espace direct et espace réciproque . . . . . . . . . . . . . . . . . . . . . . .
114 Le système hexagonal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
134.1 Indices de Miller-Bravais . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
134.2 Metrique dans le système hexagonal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
145 Retour sur la distance inter-réticulaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
156 La projection stéréographique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
187 La projection de Lambert . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
218 Les plans de glissement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
218.1 Densité atomique planaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
228.2 Cas des mailles avec plusieurs atomes par maille . . . . . . . . . . . . . . . . . . . . . . .
238.3 Application . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
239 Diffraction en condition de Bragg . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2510 Diffraction par la maille élémentaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2611 Les alliages . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2711.1Structures ordonnées dans les alliages binaires . . . . . . . . . . . . . . . . . . . . . . . .
2811.2Structure L1
0, prototype alliage CuAu, réseau cP4 (cubique à face centrée) . . . . . . . .28
11.3Structure L1
2, prototype alliage Cu3Au, cP4 (cubique à face centrée) . . . . . . . . . . .29
11.4Structure L1
1, prototype alliage CuPt, cP4 (cubique à face centrée) . . . . . . . . . . . .29
11.5StructureD1a, prototype alliage Ni4Mo, cP4 (cubique à face centrée) . . . . . . . . . . .29
11.6Structure B2, prototype alliage CuZn (cP2) . . . . . . . . . . . . . . . . . . . . . . . . . .
3012 Transition ordre-désordre dans un alliage binaire . . . . . . . . . . . . . . . . . . . . . .
3013 Détection de l"ordre chimique par diffraction . . . . . . . . . . . . . . . . . . . . . . . . .
3413.1Diffraction par un alliage A-B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3413.2Exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
361
21 Réseau de BravaisIntroduction
La découverte de la structure périodique de la matière date de 1912 quand Von Lauë découvre
la diffraction des rayons X[1]. C"est cette découverte qui a assise la vision atomistique de la ma-
tière, notion controversée jusqu"à la mise en évidence de la structure discontinue de la matière
par la diffraction des rayons X. Toutes les substances cristallisent à pression ambiante sauf l"He.
La structure périodique de la matière ne s"applique évidemment pas aux matériaux amorphes (ob-
tenus lors d"une trempe rapide par exemple empêchant la cristallisation) ou aux quasi-cristauxqui représentent cristallographiquement des exceptions (pour les règles de cristallographie à trois
dimensions). Dans ce qui suit nous nous limiterons à la cristallographie "classique" à trois dimen-
sions. 11 Réseau de Bravais
On défini un réseau périodique de Bravais par un ensemble de points qui possède une invariance
par translation discrète. Le réseau à 3D est basé sur les 3 unités élémentaires de translation
f~a1;~a2;~a3g. Un vecteur de translation~Rest décrit par un ensemble de 3 nombresfu;v;wgtel que u;v;w2Zsur la base des déplacements élémentaires de translationf~a1;~a2;~a3g. R=u~a1+v~a2+w~a3Fig. 1:a) Cellule primitive b) réseau de cellule primitiveL"ensemble des points définis par les vecteurs
n~Ro forme le réseau de Bravais. Le parallélipède défini parf~a1;~a2;~a3gest appelé la cellule primitive (voir figure 1)les angles formés par les couples de vecteurs (!a2,!a3), (!a1,!a3), (!a1,!a2) sont respectivement; ;
L"ensemble des cellules primitives pave l"espace sans lacune ni recouvrement Le nombre de coordination est le nombre de premier voisin de chaque point du réseau deBravais
-La coordination d"un réseau cubique simple est 6 -La coordination d"un réseau rectangulaire à 2D est 4Il y a 7 réseaux cristallins possibles à 3D. La liste est ci-dessous avec en correspondance, les
relations entre les longueursa1=j!a1j; a2=j!a2j; a3=j!a3jet entre les angles; ; .1Certaines figures sont au format prc qui permet à ces figures d"être visualisées en 3 dimensions à l"intérieur du fichier pdf
sans avoir besoin de l"aide d"un logiciel extérieur de visualisation (avec acrobat reader, seul logiciel le permettant à l"heure
actuelle) . On pourra donc explorer certaines structures et certaines figures d"une façon plus commode qu"à l"aide d"une
figure projettée dans le plan.quotesdbs_dbs7.pdfusesText_5[PDF] filetage double filet
[PDF] norme filetage acme
[PDF] diamètre avant filetage
[PDF] filetage double entrée
[PDF] calcul filetage metrique
[PDF] type de filetage pdf
[PDF] filetage au tour pdf
[PDF] filetage acme tableau
[PDF] trouver l'équation d'une parabole avec 2 points
[PDF] trouver la forme canonique d'une parabole
[PDF] représenter graphiquement une fonction affine
[PDF] cours fonction affine 3ème
[PDF] esprit critique cycle 3
[PDF] développement du capital humain définition
