Applications - Injections - Surjections

Fonctions injectives surjectives et bijectives

Fonctions injectives surjectives et bijectives. Injection. Définition. Une fonction g est dite injective si et seulement si tout réel de l'image correspond au

Injection surjection

http://exo7.emath.fr/ficpdf/fic00003.pdf

Cours : Ensembles et applications

Donc y = 3 n'a pas d'antécédent et f2 n'est pas surjective. 3.2. Bijection. Définition 5. f est bijective si elle injective et surjective. Cela équivaut à

MÉTHODES ET EXERCICES

— Injectivité surjectivité ou bijectivité d'une application. — Théorème d f est- elle injective

Fiche méthode : injectivité surjectivité

https://v-assets.cdnsw.com/fs/Root/bjl7l-C01_Inj_Surj_Bij_Methode.pdf

Injectif surjectif

https://dms.umontreal.ca/~broera/MAT1500Slides_190911.pdf

LAPPLICATION BIJECTIVE ET QUELQUES EXEMPLES D

I-3-3-4-autre expression pour définir les applications injective Surjective

Rappels sur les applications linéaires

− Une base étant une famille libre et génératrice et une application bijective étant injective et Comme on l'a supposé surjective on a montré qu'elle est ...

Fonctions injectives surjectives et bijectives

Fonctions injectives surjectives et bijectives. Injection. Définition. Une fonction g est dite injective si et seulement si tout réel de l'image correspond

Applications - Injections - Surjections - Bijections

20 août 2017 g est surjective. 4 Bijections. 4.1 Définition. Définition 10 : Soit f une application de E dans F. f est bijective sur F si f est injective ...

Cours : Ensembles et applications

sera la notion d'application (ou fonction) entre deux ensembles. 1. Ensembles f est bijective si elle injective et surjective.

Injection surjection

http://exo7.emath.fr/ficpdf/fic00003.pdf

MÉTHODES ET EXERCICES

Injectivité surjectivité ou bijectivité d'une application. — Théorème d'inversibilité pour la loi de composition. — Théorème de la bijection pour les

Rappels sur les applications linéaires

Une base étant une famille libre et génératrice et une application bijective étant injective et surjective le troisi`eme item est un corollaire des deux

Cours - Injections surjections

http://christophebertault.fr/documents/coursetexercices/Cours%20-%20Injections

Chapitre I Applications généralités

%20g%C3%A9n%C3%A9ralit%C3%A9s.pdf

Fiche méthode : injectivité surjectivité

https://www.pcsijbmath.sitew.fr/fs/Root/bjl7l-C01_Inj_Surj_Bij_Methode.pdf

§5.4 Injectivité surjectivité

https://www.math.univ-angers.fr/~tanlei/istia/cours21112012.pdf

DERNIÈRE IMPRESSION LE20 août 2017 à 16:21

Applications - Injections -

Surjections - Bijections

Table des matières

1 Applications2

1.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

1.2 Image d"une partie, d"une application. . . . . . . . . . . . . . . . . 3

1.3 Image réciproque d"une partie. . . . . . . . . . . . . . . . . . . . . . 3

1.4 Composition d"applications. . . . . . . . . . . . . . . . . . . . . . . 4

1.5 Ensemble d"applications. . . . . . . . . . . . . . . . . . . . . . . . . 4

1.6 Restriction et prolongement d"une application. . . . . . . . . . . . 4

2 Injections5

2.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2.2 Injection et composition. . . . . . . . . . . . . . . . . . . . . . . . . 5

2.3 Injectivité par stricte monotonie sur une partie de R. . . . . . . . . 6

3 Surjections6

3.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

3.2 Surjectivité et composition. . . . . . . . . . . . . . . . . . . . . . . . 7

4 Bijections7

4.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

4.2 Application réciproque. . . . . . . . . . . . . . . . . . . . . . . . . . 8

4.3 Bijectivité, réciproque et composition. . . . . . . . . . . . . . . . . . 9

PAUL MILAN1CPGE-L1 -ALGÈBRE

1. APPLICATIONS

1 Applications

1.1 Définition

Définition 1 :Soit deux ensemblesEetFetfune relation deEdansF. fest une application si tout élémentx?Epossède une image uniquef(x)?F. ?x?E,?!y?F,y=f(x) L"ensembleEest appelé ensemble de départ defetFl"ensemble d"arrivé def.

f(x)est appelé l"image dexparf.

Tout élémentx?Epour lequely=f(x)est appelé antécédent deyparf.

Remarque :

On pourrait aussi donner comme définition : un application deEdansFest une partie deE×Ftelle que :?x?E,?!y?F,y=f(x) Application et fonction sont synonymes. Des nuances d"ordre pédagogiques sont parfois faites entre les deux termes. Au lycée, on appelle fonction une re- lation deEdansFtelle que chaque élément deEpossède au plus une image dansF.

Exemples :

Une application représentée par undiagramme sagittal. x

1etx2ont la même imagey1.

1a deux antécédentsx1etx2.

Chaque(xi)i?[[1,4]]a une image.

Chaque(yi)i?[[1,5]]n"a pas nécessaire-

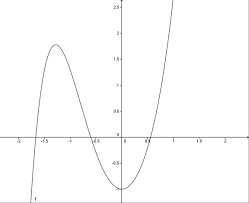
ment un antécédent. x1 x 2 x 3 x 4y 1 y 2 y 3 y 4 y 5 EfF Une applicationgdeRdansR:y1a quatre antécédentsx1,x2,x3,x4 x1x2x3x4y 1 Cg

PAUL MILAN2CPGE L1 -ALGÈBRE

1. APPLICATIONS

1.2 Image d"une partie, d"une application

Définition 2 :Soientfune application deEdansFetAune partie deE. On appelle image deAparf, l"ensemble, notéef(A), telle que : f(A) ={y?F,?a?A,y=f(a)}={f(a)}a?A L"image deEest appelée image defet notée Imf

Exemples :

A={x1,x2,x3}

f(A) ={y1,y5}

ImE={y1,y3,y5}

x 1 x 2 x 3 x 4y 1 y 2 y 3 y 4 y 5 EfF A Pour une application deRdansR: ici Img= [ymin,ymax] yminy max Cg

1.3 Image réciproque d"une partie

Définition 3 :Soientfune application deEdansFetBune partie deF. On appelle image réciproque deBparf, l"ensemble notéf-1(B), tel que : f -1(B) ={x?E,f(x)?B} ?La notationf-1(B)pourrait faire penser que la fonction réciproquef-1existe, ce qui n"est pas le cas sifn"est pas bijective. La notationf-1(B)fait simplement référence à une partie deE.

Exemples :

Par rapport à nos deux exemples, on peut écrire : f Soit la fonctionfdeRdansRdéfinie parf(x) =sinx. f -1([-1 ; 1])=Retf-1([0 ; 1])=? k?Z[ k2π;k2π+π]

PAUL MILAN3CPGE L1 -ALGÈBRE

1. APPLICATIONS

1.4 Composition d"applications

Définition 4 :Soientfetgdeux applications,f:E→Fetg:F→G. L"application composée defsuivie deg, notéeg◦f, est telle que : g◦f:?E-→G x?-→g[f(x)] Remarque :On ne peut pas nécessairement définir la composéef◦gà partir des mêmes ensembles. Dans le cas où cela serait possible, la composée de deux applications n"est pas commutative, en général :g◦f?=f◦g

1.5 Ensemble d"applications

Définition 5 :L"ensemble des applications deEdansFest notéFEouF(E,F) ?L"ensemble des applications deEdansF: notationFE

1.6 Restriction et prolongement d"une application

Définition 6 :SoitAune partie deE.

Soitf:E→Fune application.

On appelle restriction defàAl"application notéef|AdeAdansFtelle que : ?x?A,f|A(x) =f(x)

Soitf:A→Fune application.

On appelle prolongement defàEl"application notéegdeEdansFtelle que : ?x?A,f(x) =g(x) Remarque :Quand une fonction admet une limite à l"une des bornes ouvertes finies de son ensemble de définition, on peut prolonger la fonction par continuité. Par exemple la fonctionfdéfinie surR?par :f(x) =sinx x. Or limx→0f(x) =1.

On prolonge alors la fonctionfsurR:???f(x) =sinx

xx?=0 f(0) =1

PAUL MILAN4CPGE L1 -ALGÈBRE

2. INJECTIONS

2 Injections

2.1 Définition

Définition 7 :Soit l"applicationfdeEdansF.

fest injective surEsi tout élément deFpossède au plus un antécédent : ?x1,x2?E,f(x1) =f(x2)?x1=x2

Remarque :

On a le diagramme sagittal suivant :

Certains éléments deFpeuvent ne pas

avoir d"antécédent. C"est la cas ici dey4.

Imf={y1,y2,y3,y5}?=F

card(E)?card(F) x1 x 2 x 3 x 4y 1 y 2 y 3 y 4 y 5 EfF

Exemple :L"applicationf:z?→f(z) =z+i

z-iest injective surC/{i}car : z 1+i z1-i=z2+iz2-i?(z1+i)(z2-i) = (z1-i)(z2+i)? z

1z2+i(z2-z1) +1=z1z2+i(z1-z2) +1?z2-z1=z1-z2?

2(z2-z1) =0?z2=z1

2.2 Injection et composition

Définition 8 :Soientfetgdeux applications,f:E→Fetg:F→G. Sifetgsont injectives alorsg◦fest injective.

Sig◦fest injective alorsfest injective

Remarque :Sig◦fest injective alorsgrien du tout. Contre exemplefetgsont respectivement la fonction exponentielle et la fonction carrée définies surR.

La fonction exponentielle est injective

g◦f(x) = (ex)2=e2xdoncg◦fest injective. La fonction carrée n"est pas injective car 4 a deux antécédents 2 et-2.

Démonstration :

fetginjectives.

g◦f(x1) =g◦f(x2)?g[f(x1)]=g[f(x2)]ginjective?f(x1) =f(x2)finjective?x1=x2

g◦finjective

f(x1) =f(x2)composition parg?g[f(x1)]=g[f(x2)]g◦finjective?x1=x2

PAUL MILAN5CPGE L1 -ALGÈBRE

3. SURJECTIONS

2.3 Injectivité par stricte monotonie sur une partie de R

Théorème 1 :SoientAune partie deRetfune fonction deAdansR. Sifest strictement monotone surAalorsfest injective surA

Remarque :La réciproque est fausse

carfpeut être injective surAsans être monotone surA.Dans cecaslafonction fn"est pas continue surA.

Exemples :

La fonction cos est injective sur[0 ;π]car strictement décroissante. On en dé- duit l"implication sur[0 ;π], cosx=cosy?x=y. Il est à remarquer que cette implication n"est pas vrai surRcar la fonction cos est périodique. Montrons que?x,y?]-1 ; 1[, arctanx+arctany=arctanx+y1-xy ?x?]-1 ; 1[, arctanx??

4;π4?

?arctanx+arctany?? -π2;π2? tan(arctanx+arctany) =tanarctanx+tanarctany1-tanarctanxtanarctany=x+y1-xy=tanarctanx+y1-xy

La fonction tan est strictement croissante sur

2;π2?

quotesdbs_dbs11.pdfusesText_17

[PDF] Applications - Injections - Surjections - Bijections

Applications - Injections -

Surjections - Bijections

Table des matières

1 Applications2

1.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

1.2 Image d"une partie, d"une application. . . . . . . . . . . . . . . . . 3

1.3 Image réciproque d"une partie. . . . . . . . . . . . . . . . . . . . . . 3

1.4 Composition d"applications. . . . . . . . . . . . . . . . . . . . . . . 4

1.5 Ensemble d"applications. . . . . . . . . . . . . . . . . . . . . . . . . 4

1.6 Restriction et prolongement d"une application. . . . . . . . . . . . 4

2 Injections5

2.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2.2 Injection et composition. . . . . . . . . . . . . . . . . . . . . . . . . 5

2.3 Injectivité par stricte monotonie sur une partie de R. . . . . . . . . 6

3 Surjections6

3.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

3.2 Surjectivité et composition. . . . . . . . . . . . . . . . . . . . . . . . 7

4 Bijections7

4.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

4.2 Application réciproque. . . . . . . . . . . . . . . . . . . . . . . . . . 8

4.3 Bijectivité, réciproque et composition. . . . . . . . . . . . . . . . . . 9

PAUL MILAN1CPGE-L1 -ALGÈBRE

1. APPLICATIONS

1 Applications

1.1 Définition

f(x)est appelé l"image dexparf.

Remarque :

Exemples :

1etx2ont la même imagey1.

1a deux antécédentsx1etx2.

Chaque(xi)i?[[1,4]]a une image.

Chaque(yi)i?[[1,5]]n"a pas nécessaire-

PAUL MILAN2CPGE L1 -ALGÈBRE

1. APPLICATIONS

1.2 Image d"une partie, d"une application

Exemples :

A={x1,x2,x3}

ImE={y1,y3,y5}

1.3 Image réciproque d"une partie

Exemples :

PAUL MILAN3CPGE L1 -ALGÈBRE

1. APPLICATIONS

1.4 Composition d"applications

1.5 Ensemble d"applications

1.6 Restriction et prolongement d"une application

Définition 6 :SoitAune partie deE.

Soitf:E→Fune application.

Soitf:A→Fune application.

On prolonge alors la fonctionfsurR:???f(x) =sinx

PAUL MILAN4CPGE L1 -ALGÈBRE

2. INJECTIONS

2 Injections

2.1 Définition

Définition 7 :Soit l"applicationfdeEdansF.

Remarque :

On a le diagramme sagittal suivant :

Certains éléments deFpeuvent ne pas

Imf={y1,y2,y3,y5}?=F

Exemple :L"applicationf:z?→f(z) =z+i

1z2+i(z2-z1) +1=z1z2+i(z1-z2) +1?z2-z1=z1-z2?

2(z2-z1) =0?z2=z1

2.2 Injection et composition

Sig◦fest injective alorsfest injective

La fonction exponentielle est injective

Démonstration :

fetginjectives.

g◦finjective

PAUL MILAN5CPGE L1 -ALGÈBRE

3. SURJECTIONS

2.3 Injectivité par stricte monotonie sur une partie de R

Remarque :La réciproque est fausse

Exemples :

4;π4?

La fonction tan est strictement croissante sur

2;π2?

f(x)est appelé l"image dexparf.

A={x1,x2,x3}

Soitf:E→Fune application.

Soitf:A→Fune application.

Sig◦fest injective alorsfest injective

La fonction exponentielle est injective

fetginjectives.

g◦finjective