 Cours Mécanique Rationnelle
Cours Mécanique Rationnelle
Après une rappelle mathématique sur les vecteurs et les torseurs ce polycopié aborde les trois axes fondamentaux de la mécanique: la statique
 COURS DE MÉCANIQUE RATIONNELLE Dr MA BOUZIDI
COURS DE MÉCANIQUE RATIONNELLE Dr MA BOUZIDI
MECANIQUE RATIONNELLE Cours & exercices résolus.(2008). 6-A.Timmermans .Traité de mécanique rationnelle. (1962). 7-C.Pasquier PeiP Polytech
 MECANIQUE RATIONNELLE
MECANIQUE RATIONNELLE
Page 1. FFa. MECANIQUE. RATIONNELLE. Cours & exercices résolus. Rappels sur les mécanique classique notamment en mécanique des solides. L'utilisation des ...
 Mécanique rationnelle
Mécanique rationnelle
Dans ce cours la mécanique regroupera le calcul vectoriel
 MECANIQUE RATIONNELLE
MECANIQUE RATIONNELLE
A3. A4. Page 17. Cours de mécanique rationnelle (F322). UTMBéchar. Pr REBHI MEBROUK. 9. 2.9.3) Forces coplanaires parallèles : 2.9.3.1) Cas de forces parallèles
 LIVRE-MECANIQUE-RATIONNELLE-2017.pdf
LIVRE-MECANIQUE-RATIONNELLE-2017.pdf
Ce livre d'introduction à la mécanique rationnelle contient des cours détaillés avec des applications résolues et des exercices supplémentaires non résolus.
 La Mécanique Rationnelle
La Mécanique Rationnelle
10 déc. 2005 L'Objectif d'un cours de mécanique est de savoir mettre sous forme mathématique une situation physique. Les expériences décrites dans un cours ...
 Duhem et la Mécanique rationnelle et expérimentale de Bouasse
Duhem et la Mécanique rationnelle et expérimentale de Bouasse
1 août 2010 Le but de la mécanique ayant été ainsi défini les règles qui doivent diriger son enseignement s'en déduisent
 MECANIQUE rationnelle kadi ali.pdf
MECANIQUE rationnelle kadi ali.pdf
21 oct. 2016 ... de physique. Cours exercices Mécanique Rationnelle : TCT et LMD-ST sem :3. 43. A.KADI. On peut vérifier facilement : 0. 30. 30. 6. 2. 106. 5.
 H. Bouasse. — Cours de mécanique rationnelle et expérimentale
H. Bouasse. — Cours de mécanique rationnelle et expérimentale
— Cours de mécanique rationnelle et expérimentale spécialement écrit pour les physiciens et les ingénieurs. — 1 vol. gr. in-8°
 Cours Mécanique Rationnelle
Cours Mécanique Rationnelle
FACULTE DE PHYSIQUE. Cours. Mécanique Rationnelle. Salim BAADJ. Ce cours est destiné aux étudiants 2 éme. ANNEE LMD. Domaine Sciences et Technologies.
 Mécanique Rationnelle 2
Mécanique Rationnelle 2
Mécanique Rationnelle 2. Syllabus d'exercices. Pierre LAMBERT En cours de mouvement ce disque roule sans glisser sur la piste.
 Physique-IV-Mécanique-Rationnelle.pdf
Physique-IV-Mécanique-Rationnelle.pdf
Polycopié. Physique IV : Mécanique Rationnelle. COURS et Exercices. (Unité Fondamentale-- Domaine Sciences et Technique – S03 Licence LMD). Dr. MEBREK MOUED.
 Mécanique rationnelle
Mécanique rationnelle
Dans ce cours la mécanique regroupera le calcul vectoriel
 COURS DE MÉCANIQUE RATIONNELLE Dr MA BOUZIDI
COURS DE MÉCANIQUE RATIONNELLE Dr MA BOUZIDI
Faculté de Technologie. Département de Génie Civil. COURS DE MÉCANIQUE. RATIONNELLE. Préparé par: Dr. BOUZIDI Mohamed Amin. 2016/2017
 Mécanique Rationnelle II
Mécanique Rationnelle II
Service de Mécanique Rationnelle. Dynamique et Vibrations. Notes de cours `a l'intention des étudiants de 2e Bachelier. Mécanique Rationnelle II.
 Mécanique rationnelle
Mécanique rationnelle
Le cours permet aux étudiants du premier cycle universitaire une compréhension des principes fondamentaux de la mécanique rationnelle. Cette polycopie est
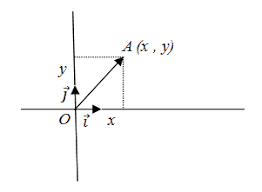
 The first chapter is devoted to the theory of vectors and develops the
The first chapter is devoted to the theory of vectors and develops the
Cours de Mécanique Rationnelle. By J. Chazy. Tome I: Dynamique du Point. Material. Paris Gauthier-Villars
 Bachelier en sciences de lingénieur orientation ingénieur civil
Bachelier en sciences de lingénieur orientation ingénieur civil
Mécanique rationnelle I
 Duhem et la Mécanique rationnelle et expérimentale de Bouasse
Duhem et la Mécanique rationnelle et expérimentale de Bouasse
1 août 2010 Lorsque Duhem publie l'analyse de Mécanique rationnelle et expérimentale ... cours de Mécanique à la fois rationnelle et expérimentale. ».
FACULTE POLYTECHNIQUE DE MONS
Service de M´ecanique Rationnelle,
Dynamique et Vibrations
Notes de cours `a l"intention
des ´etudiants de 2eBachelierM´ecanique Rationnelle II
- Notes de cours -Prof. Calogero CONTI, Prof. Serge BOUCHER
Septembre 2007
Table des mati`eres1 Grandeurs cin´etiques1
1.1 D´efinition des grandeurs cin´etiques . . . . . . . . . . . . . . .. . . . . . . . . . . 1
1.1.1 Le torseur des r´eactions d"inertie
?R(-ma),?M(-ma)O. . . . . . . . . . . . . 11.1.2 Le torseur des quantit´es de mouvement
?P,?LO. . . . . . . . . . . . . . . 41.1.3 L"´energie cin´etiqueT. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2 Th´eor`emes g´en´eraux de la cin´etique . . . . . . . . . . . . .. . . . . . . . . . . . 5
1.2.1 Relation entre la r´esultante des r´eactions d"inertie et la r´esultante des
quantit´es de mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61.2.2 Relation entre le moment des r´eactions d"inertie et le moment cin´etique . 6
1.2.3 Relation entre les r´esultantes des deux torseurs cin´etiques et le mouvement
du centre de gravit´e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71.3 Th´eor`eme de Ko¨enig - Mouvement d"un syst`eme m´ecanique autour de son centre
de masse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81.3.1 Expression des torseurs cin´etiques relatifs au centre de gravit´e G dans le
mouvement par rapport au rep`ere de Ko¨enig . . . . . . . . . . . . . .. . 81.3.1.1 Torseur des quantit´es de mouvement au centre de gravit´eG/Sk8
1.3.1.2 Torseurs des r´eactions d"inertie au centre de gravit´eG/Sk. . . . 9
1.3.2 Th´eor`emes de Ko¨enig (ou th´eor`emes de transport). . . . . . . . . . . . . 10
1.4 Propri´et´es d"inertie d"un solide . . . . . . . . . . . . . . . . .. . . . . . . . . . . 12
1.4.1 Tenseur d"inertie en un point . . . . . . . . . . . . . . . . . . . . .. . . . 12
1.4.2 Matrice d"inertie en un point . . . . . . . . . . . . . . . . . . . . .. . . . 13
1.4.3 Moments d"inertie par rapport `a une droite et produits d"inertie par rap-
port `a deux droites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131.4.4 Propri´et´es de variance tensorielle . . . . . . . . . . . . .. . . . . . . . . . 14
1.4.5 Inertie de solides `a masse r´epartie continue . . . . . .. . . . . . . . . . . 15
1.4.6 Signification du moment d"inertie en relation avec la projection du moment
cin´etique sur l"axe de rotation . . . . . . . . . . . . . . . . . . . . . . .. . 151.4.7 Rayon de giration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16
1.4.8 Propri´et´es d"inertie centrales . . . . . . . . . . . . . . . .. . . . . . . . . 16
iTABLE DES MATI`ERESii
1.4.9 Tenseur d"inertie de solides homog`enes de forme g´eom´etrique simple . . . 16
1.4.9.1 Circonf´erence homog`ene, par rapport `a l"axeOzpassant par son
centreOou coque cylindrique circulaire homog`ene, par rapport `a son axeOz. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161.4.9.2 Sph`ere homog`ene . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.4.9.3 Parall´el´epip`ede rectangle, plaque plane et barre par rapport `a
des axes passant par leur centre de gravit´eOet parall`eles aux cˆot´es . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171.4.9.4 Cylindre et disque par rapport `a leur axeOz, et `a deux axes
perpendiculaires `a celui-ci . . . . . . . . . . . . . . . . . . . . . . 191.4.10 Transposition des propri´et´es d"inertie en un autre pˆole - Th´eor`eme des
axes parall`eles (ou th´eor`eme de Steiner) . . . . . . . . . . . . .. . . . . . 201.4.11 Transposition des propri´et´es d"inertie `a d"autres directions - Variance ten-
sorielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231.5 Exercices `a r´esoudre sur la notion d"inertie . . . . . . . .. . . . . . . . . . . . . . 24
1.5.1 Tenseur d"inertie d"un syst`eme disque + cylindre . . .. . . . . . . . . . . 24
1.5.2 Disque en rotation non align´e par rapport `a son axe . .. . . . . . . . . . 24
1.5.3 Axes principaux d"inertie . . . . . . . . . . . . . . . . . . . . . . .. . . . 24
1.5.3.1 Propri´et´es d"un axe principal central . . . . . . . . .. . . . . . . 27
1.6 Solide dynamiquement de r´evolution . . . . . . . . . . . . . . . .. . . . . . . . . 27
1.7 Relation entre moments d"inertie m´ecanique et g´eom´etrique . . . . . . . . . . . . 28
1.8 Cas plan de la cin´etique . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . 28
1.9 M´ethodes de d´etermination du torseur des r´eactions d"inertie et de l"´energie
cin´etique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .301.9.1 R´esultante des r´eactions d"inertie
?R(-m?a)S/s. . . . . . . . . . . . . . . . . 301.9.2 Moment
?M(-m?a)Odes r´eactions d"inertie au point O . . . . . . . . . . . . 301.9.2.1 D´erivation du moment cin´etique au mˆeme pointO. . . . . . . . 31
1.9.2.2 En passant par le centre de gravit´eGet le th´eor`eme de Ko¨enig . 32
1.9.2.3 En passant par un autre point point P mieux adapt´e pour l"ex-
pression du moment des r´eactions d"inertie . . . . . . . . . . . . 331.9.3 Energie cin´etiqueT. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
1.9.3.1 S"il existe un point O tel que sa vitesse instantan´ee soit nulle . . 33
1.9.3.2 M´ethode g´en´erale bas´ee sur le th´eor`eme de Ko¨enig . . . . . . . . 34
1.10 Cin´etique d"un solide en rotation autour d"un axe fixe .. . . . . . . . . . . . . . 34
1.11 Tests de compr´ehension sur l"inertie et les grandeurscin´etiques . . . . . . . . . . 37
1.11.1 Tige en rotation autour d"un axe . . . . . . . . . . . . . . . . . .. . . . . 37
1.11.2 Plaque tournant autour d"un axe . . . . . . . . . . . . . . . . . .. . . . . 38
1.11.3 Moto roulant sans glisser . . . . . . . . . . . . . . . . . . . . . . .. . . . 39
Cours de M´ecanique Rationnelle IIProf. C. Conti, Prof. S. BoucherTABLE DES MATI`ERESiii
1.12 Exercices `a r´esoudre sur les notions de grandeurs cin´etiques . . . . . . . . . . . . 40
1.12.1 Transmission par roues dent´ees . . . . . . . . . . . . . . . . .. . . . . . . 40
1.12.2 Plaque en rotation - Conditions d"´equilibrage d"unsolide en rotation au-
tour d"un axe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 401.12.3 Rotation autour d"un axe vertical, du bˆati d"une foreuse en fonctionnement
- Manifestation du couple gyroscopique . . . . . . . . . . . . . . . . .. . 402 Th´eor`emes g´en´eraux de la dynamique42
2.1 Principe fondamental de la Dynamique . . . . . . . . . . . . . . . .. . . . . . . . 43
2.1.1 Principe fondamental en rep`ere galil´een . . . . . . . . .. . . . . . . . . . 43
2.1.2 Principe fondamental en rep`ere non galil´een . . . . . .. . . . . . . . . . . 44
2.1.3 Principe fondamental en rep`ere g´eocentrique . . . . .. . . . . . . . . . . 45
2.1.4 Principe fondamental par rapport `a des axes li´es `a la terre . . . . . . . . . 50
2.1.4.1 Direction du vecteur?g. . . . . . . . . . . . . . . . . . . . . . . . 52
2.1.4.2 Grandeur du vecteur gravit´e?get de l"attraction terrestre?Hpar
unit´e de masse . . . . . . . . . . . . . . . . . . . . . . . . . . . . 522.1.4.3 Diff´erence entre jour solaire et jour sid´eral . . . .. . . . . . . . 53
2.1.5 Exemple : masse ponctuelle glissant sans perte sur unetige horizontale
en rotation. R´esolution en appliquant le principe fondamental de la dyna- mique - Equilibre des forces . . . . . . . . . . . . . . . . . . . . . . . . . . 542.2 Principe de d"Alembert . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 56
2.2.1 Application du principe des puissances virtuelles . .. . . . . . . . . . . . 57
2.2.1.1 Rappels de m´ecanique analytique . . . . . . . . . . . . . . .. . 58
2.2.1.2 M´ethodologie d"application du principe des puissances virtuelles
- D´emonstration . . . . . . . . . . . . . . . . . . . . . . . . . . . 582.2.2 Exemple : masse ponctuelle glissant sans perte sur unetige horizontale en
rotation - R´esolution par application du principe des puissances virtuelles 602.3 Conditions initiales - Etat dynamique . . . . . . . . . . . . . . .. . . . . . . . . 61
2.4 Th´eor`emes g´en´eraux de la Dynamique . . . . . . . . . . . . . .. . . . . . . . . . 62
2.4.1 Th´eor`eme de la quantit´e de mouvement et th´eor`emedu centre de masse . 62
2.4.1.1 Cas particuliers . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
2.4.2 Th´eor`eme du moment cin´etique . . . . . . . . . . . . . . . . . .. . . . . . 63
2.4.2.1 Exemple - Equation du mouvement d"un solide en rotation per-
manente autour d"un axe fixeOz. . . . . . . . . . . . . . . . . . 642.4.3 Quelques corollaires et interpr´etation . . . . . . . . . .. . . . . . . . . . . 65
2.4.4 Exercices en application des th´eor`emes g´en´erauxde la dynamique . . . . 66
2.4.4.1 Mouvement d"une barque dont un passager se d´eplace. . . . . . 66
2.4.4.2 Mouvement d"un disque sur lequel se d´eplace un animal . . . . . 66
Cours de M´ecanique Rationnelle IIProf. C. Conti, Prof. S. BoucherTABLE DES MATI`ERESiv
2.5 Th´eor`eme de l"´energie cin´etique (ou th´eor`eme desforces vives) . . . . . . . . . . 66
2.5.1 Expression du th´eor`eme de l"´energie cin´etique . .. . . . . . . . . . . . . . 66
2.5.2 Application du th´eor`eme de l"´energie cin´etique dans le cas d"un syst`eme
conservatif . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 682.5.2.1 Cas de liaisons sans perte et ind´ependantes du temps . . . . . . 69
2.5.2.2 Cas de forces appliqu´ees d´erivant d"une ´energiepotentielle
ind´ependante du temps . . . . . . . . . . . . . . . . . . . . . . . 702.5.2.3 Exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
2.5.2.4 Formulation pour un syst`eme conservatif . . . . . . . .. . . . . 72
2.5.2.5 Exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
2.5.3 Exercice en application du th´eor`eme de l"´energie cin´etique . . . . . . . . . 74
2.5.3.1 Mouvement d"un motocycliste . . . . . . . . . . . . . . . . . . .74
2.5.4 Comparaison avec le premier principe de la Thermodynamique . . . . . . 74
2.6 Cas plan de la dynamique du solide . . . . . . . . . . . . . . . . . . . .. . . . . . 75
2.7 Invariance des th´eor`emes g´en´eraux et g´en´eralisation du th´eor`eme du moment
cin´etique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .772.8 Tests de compr´ehension sur les th´eor`emes g´en´erauxde la dynamique . . . . . . . 78
2.9 Exercices sur les th´eor`emes g´en´eraux de la dynamique . . . . . . . . . . . . . . . 81
2.9.1 Poulie roulant sur un plan horizontal grˆace `a deux ergots . . . . . . . . . 81
2.9.2 Mouvement d"un syst`eme roue et tige glissant avec frottement . . . . . . 82
2.9.3 Mouvements d"un carrousel . . . . . . . . . . . . . . . . . . . . . . .. . . 82
2.9.4 Appontage d"un avion . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 83
3 Vibrations des Syst`emes M´ecaniques `a un degr´e de libert´e 85
3.1 Mouvement libre d"un syst`eme `a 1 degr´e de libert´e . . .. . . . . . . . . . . . . . 85
3.1.1 Equation diff´erentielle du mouvement libre d"un syst`eme `a 1 degr´e de libert´e 85
3.1.1.1 Mouvement horizontal d"une masse glissant sans perte soumise
`a des forces ´elastiques et d"amortissement . . . . . . . . . . . .. 853.1.1.2 Mouvement vertical d"une masse ponctuelle soumise`a des forces
´elastiques et d"amortissement . . . . . . . . . . . . . . . . . . . . 863.1.2 Rappels sur la r´esolution d"une ´equation diff´erentielle homog`ene `a coeffi-
cients constants . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 883.1.3 Lois du mouvement libre d"un syst`eme lin´eaire vibrant amorti `a 1 degr´e
de libert´e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 883.1.3.1 Cas d"un syst`eme non amortiξ= 0 . . . . . . . . . . . . . . . . 89
3.1.3.2 Cas g´en´eral d"un syst`eme amortiξ >0 . . . . . . . . . . . . . . 90
3.1.3.3 Analyse d´etaill´ee de l"´evolution correspondant `a une loi du mou-
vement pseudo-p´eriodique . . . . . . . . . . . . . . . . . . . . . . 93 Cours de M´ecanique Rationnelle IIProf. C. Conti, Prof. S. BoucherTABLE DES MATI`ERESv
3.1.4 D´etermination exp´erimentale du degr´e d"amortissement . . . . . . . . . . 95
3.1.4.1 Si le syst`eme oscille autour de z´ero . . . . . . . . . . . .. . . . . 95
3.1.4.2 Deuxi`eme m´ethode : en d´eterminant directement le d´ecr´ement
logarithmique . . . . . . . . . . . . . . . . . . . . . . . . . . . . 963.1.4.3 Si le syst`eme n"oscille pas autour de 0 . . . . . . . . . . .. . . . 97
3.1.4.4 Influence du frottement sec . . . . . . . . . . . . . . . . . . . . .99
3.1.5 Aspects ´energ´etiques en mouvement libre . . . . . . . . .. . . . . . . . . 101
3.1.5.1 Bilan ´energ´etique dans le cas d"un syst`eme amorti . . . . . . . . 102
3.1.5.2 Bilan ´energ´etique dans le cas d"un syst`eme non amorti . . . . . 104
3.2 Mouvement forc´e d"un syst`eme `a un degr´e de libert´e ... (cas g´en´eral) . . . . . . . 104
3.2.1 Equation diff´erentielle du mouvement . . . . . . . . . . . . .. . . . . . . 104
3.2.2 Lin´earisation de l"´equation diff´erentielle du mouvement lorsque le syst`eme
est soumis `a des forces ´elastiques non lin´eaires . . . . . . .. . . . . . . . 1053.2.3 Rappels sur la r´esolution d"une ´equation diff´erentielle lin´eaire `a coefficients
constants . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1063.2.3.1 Int´egrale g´en´erale - Int´egrale particuli`ere. . . . . . . . . . . . . 106
3.2.3.2 Propri´et´es . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
3.2.3.3 Solution g´en´erale de l"´equation non homog`ene .. . . . . . . . . 107
3.2.3.4 Principaux types d"excitationf(t) . . . . . . . . . . . . . . . . . 108
3.3 Mouvement forc´e d"un syst`eme `a un degr´e de libert´e ... (excitation harmonique) 108
3.3.1 Solution globale en transitoire . . . . . . . . . . . . . . . . . .. . . . . . . 108
3.3.2 Mouvement sinuso¨ıdal en r´egime - R´eponse harmonique - Courbe d"am-
plification dynamiqueG1. . . . . . . . . . . . . . . . . . . . . . . . . . . 1113.3.3 Interpr´etation de l"´evolution fr´equentielle desr´eponses harmoniques en
amplitude et en phase - Aspects physiques et math´ematiques .. . . . . . 1163.3.4 Interpr´etation de l"´evolution fr´equentielle desr´eponses harmoniques en
amplitude et en phase - Visualisation dans le plan complexe .. . . . . . . 1163.3.5 Aspects ´energ´etiques du comportement d"un syst`eme m´ecanique amorti
soumis `a une excitation harmonique . . . . . . . . . . . . . . . . . . . .. 1183.3.5.1 Energie d´evelopp´ee par la force d"excitation harmonique durant
un cycle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1183.3.5.2 Egalit´e sur un cycle entre l"´energie dissip´ee par l"amortisseur et
l"´energie fournie . . . . . . . . . . . . . . . . . . . . . . . . . . . 1193.3.5.3 Energie dissip´ee par l"amortisseur durant un cycle . . . . . . . . 120
3.3.6 R´eponse dans le cas particulier (th´eorique) o`u l"amortissement est nul . . 121
3.4 Mouvement forc´e d"un syst`eme `a un degr´e de libert´e ... (excitation par balourd) 122
3.4.1 Equation diff´erentielle du mouvement . . . . . . . . . . . . .. . . . . . . 122
3.4.2 Mouvement sinuso¨ıdal en r´egime - Courbe de gainG2. . . . . . . . . . . 123
Cours de M´ecanique Rationnelle IIProf. C. Conti, Prof. S. BoucherTABLE DES MATI`ERESvi
3.4.3 Force dynamique transmise au sol - Courbe de transmissibilit´eT. . . . . 125
3.5 Mouvement forc´e d"un syst`eme `a un degr´e de libert´e ... (excitation par la base) . 128
3.5.1 Equation diff´erentielle du mouvement . . . . . . . . . . . . .. . . . . . . 128
3.5.2 Mouvement sinuso¨ıdal en r´egime - Courbe de transmissibilit´eT. . . . . . 129
3.6 Mouvement forc´e d"un syst`eme `a un degr´e de libert´e (excitation p´eriodique) . . . 131
3.6.1 Rappels sur la d´ecomposition en s´eries de Fourier . .. . . . . . . . . . . . 131
3.6.2 ´Etude de la r´eponse de r´egime lorsque l"excitation est p´eriodique . . . . . 1333.6.3 Application `a la dynamique des syst`emes m´ecaniques : importance du
domaine fr´equentiel pour les vibrations m´ecaniques . . . .. . . . . . . . . 1343.6.4 Application en m´etrologie : reproduction d"un signal d"entr´ee . . . . . . . 135
3.7 R´eponse indicielle d"un syst`eme m´ecanique lin´eaire `a un degr´e de libert´e ... . . . 136
3.7.1 Equation diff´erentielle du mouvement . . . . . . . . . . . . .. . . . . . . 136
3.7.2 Utilisation de la r´eponse indicielle en m´etrologie. . . . . . . . . . . . . . 138
3.7.3 Utilisation de la r´eponse indicielle pour la d´etermination de la r´eponse `a
une excitation quelconque . . . . . . . . . . . . . . . . . . . . . . . . . . . 1383.8 R´eponse impulsionnelle des syst`emes `a un degr´e de libert´e (ou r´eponse balistique) 140
3.8.1 Equation diff´erentielle du mouvement . . . . . . . . . . . . .. . . . . . . 140
3.8.1.1 Utilisation de la r´eponse impulsionnelle pour la d´etermination `a
une excitation quelconque . . . . . . . . . . . . . . . . . . . . . . 1423.8.2 Relation entre r´eponse impulsionnellez(t) et r´eponse indicielleg(t) . . . . 143
3.9 Syst`emes du premier ordre . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 143
3.9.1 Equation diff´erentielle du mouvement - R´eduction `al"ordre 1 . . . . . . . 143
3.9.2 R´eponse en mouvement libre . . . . . . . . . . . . . . . . . . . . . .. . . 144
3.9.3 R´eponse indicielle d"un syst`eme du premier ordre . .. . . . . . . . . . . . 144
3.9.4 R´eponse harmonique d"un syst`eme du premier ordre . .. . . . . . . . . . 146
3.10 Capteurs d"acc´el´eration et de vitesse . . . . . . . . . . . .. . . . . . . . . . . . . 147
3.10.1 Principe d"un acc´el´erom`etre pi´ezo´electrique. . . . . . . . . . . . . . . . . 148
3.10.2 Caract´eristique fr´equentielle d"un acc´el´erom`etre . . . . . . . . . . . . . . . 148
3.10.3 Les capteurs de vitesse . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 151
3.10.3.1 Principe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151
3.10.3.2 Caract´eristique fr´equentielle d"un capteur devitesse . . . . . . . 151
3.11 Mouvements pendulaires . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 153
3.11.1 Pendule simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 153
3.11.2 Pendule compos´e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 155
3.11.3 Syst`emes m´ecaniques dont l"´equation du mouvement est identique `a celle
du pendule . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156 Cours de M´ecanique Rationnelle IIProf. C. Conti, Prof. S. BoucherTABLE DES MATI`ERESvii
3.12 Exemples de formulation des ´equations du mouvement pour des syst`emes `a un ddl156
3.12.1 Disque oscillant autour d"un axe vertical . . . . . . . . .. . . . . . . . . . 156
3.12.2 Table vibrant horizontalement excit´ee par un balourd en rotation . . . . . 158
3.13 Raideur ´equivalente pour diff´erents syst`emes . . . . .. . . . . . . . . . . . . . . . 159
3.14 Tests de compr´ehension sur les th´eor`emes g´en´eraux de la dynamique . . . . . . . 161
3.15 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 164
3.15.1 Vibrations subie par un cycliste . . . . . . . . . . . . . . . . .. . . . . . . 164
3.15.2 Stabilisation d"une plate forme sur un bateau . . . . . .. . . . . . . . . . 165
3.15.3 Exercice : appontage d"un avion . . . . . . . . . . . . . . . . . .. . . . . 166
4 Percussions - Gyroscopie - Equilibrage167
4.1 Percussions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 167
4.1.1 Choc entre deux solides : hypoth`eses de la m´ecaniquerationnelle . . . . . 167
4.1.2 Applications des th´eor`emes g´en´eraux de la dynamique `a la phase de choc 168
4.1.2.1 Th´eor`eme de la quantit´e de mouvement . . . . . . . . . .. . . . 168
4.1.2.2 Th´eor`eme du moment cin´etique . . . . . . . . . . . . . . . .. . 168
4.1.3 D´efinition du vecteur percussion et ´equations d"´equilibre dans le cas d"une
percussion unique sur un solide . . . . . . . . . . . . . . . . . . . . . . . .1694.1.4 Cas des percussions multiples . . . . . . . . . . . . . . . . . . . .. . . . . 172
4.1.5 Centre des percussions et percussion sur un pendule compos´e . . . . . . . 172
4.1.6 D´efinition du coefficient de restitution et aspects ´energ´etiques . . . . . . 175
4.1.6.1 D´etermination du coefficient de restitution. Rebond d"une bille . 176
4.1.6.2 Evolution temporelle du rebond d"une bille . . . . . . .. . . . . 177
4.1.6.3 Interpr´etation ´energ´etique du coefficient de restitution . . . . . . 178
4.1.7 Validit´e de la th´eorie des percussions . . . . . . . . . . .. . . . . . . . . . 179
4.2 Equilibrage d"un solide autour d"un axe . . . . . . . . . . . . . .. . . . . . . . . 179
4.2.1 Equations d"´equilibre dynamique d"un solide en rotation autour d"un axe
fixe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1794.2.2 Caract´eristiques d"´equilibrage d"un rotor . . . . . .. . . . . . . . . . . . . 181
4.2.2.1 Equilibrage statique . . . . . . . . . . . . . . . . . . . . . . . . .181
quotesdbs_dbs19.pdfusesText_25[PDF] mécanique rationnelle pdf usthb
[PDF] mécanique rationnelle statique
[PDF] mécanique rationnelle usthb
[PDF] mécanique terminale s exercices
[PDF] mecanique vibratoire
[PDF] mécanisme d'action toxique des salicylés
[PDF] mécanisme de défense des plantes
[PDF] mecanisme de financement definition
[PDF] mécanisme de financement des projets de développement
[PDF] mécanisme de la faim
[PDF] mécanisme de la photosynthèse
[PDF] mécanisme de régulation de la faim
[PDF] mecanisme du commerce mondial
[PDF] mécanisme réactionnel chimie organique exercices
