Limites et asymptotes
−→ A faire en TD : cas des polynômes et des fractions rationnelles. IV. Interprétation graphique et asymptotes. 1) Asymptote horizontale. Si lim x→
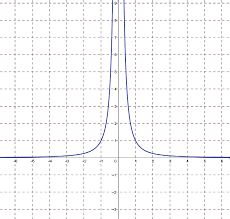Exemples de limites dune fonction en un réel. Interprétation graphique
Exemples de limites d'une fonction en un réel. Interprétation graphique. Définition. Soit a un nombre réel. On dit que le réel x tend vers a et on note x a.
Dérivée dune fonction et interprétation graphique
Graphiquement cela signifie que le point M se rapproche du point M0. La tangente est ainsi la « droite limite » ainsi obtenue. Équation de la tangente à Cf. On
Concordance entre deux méthodes de mesure dune même variable
12 nov. 2015 Le diagramme de Bland et Altman permet une représentation graphique de ces données. ... limites de concordance à 95 % proches. On peut dire que ...
Consigne : déterminer une limite interpréter graphiquement une limite
Interprétation graphique : La courbe qui représente f présente : • une asymptote horizontale d'équation = 1 en +∞. (f( ) se rapproche du niveau y = 1
Développements limités
I.4 Interprétation graphique . On retrouve bien le développement limité à l'ordre 6 de cos(x). Propriété 7. Soit F une primitive de f sur un intervalle I ...
Limites et asymptotes
−→ on traitera en TD tous les cas pour les polynômes et les fractions rationnelles. IV. Interprétation graphique et asymptotes. 1) Asymptote horizontale. Si
INTERPRÉTATION DES DONNÉES DE POMPAGES DESSAI
Courbe /ásf (log.t) . Effet des limites la Urales. S A.1.2. et L^.22. Fig.10- Graphique permettant l
Cours sur les limites - 2020
Interprétation graphique. LIMITES EN UN REEL – INTERPRETATION GRAPHIQUE https://bit.ly/3amk769. Trois cas peuvent se présenter dans le calcul de limite en un
Limites de fonctions – Comportement asymptotique - Exercices
limites d'une fonction f. Donner une interprétation graphique de chacune de ces limites. Exercice 3 corrigé disponible. Déterminer les limites suivantes :.
Limites et asymptotes
1) Limite infinie à l'infini On dit que f a pour limite +? en +? et on note lim ... Interprétation graphique et asymptotes. 1) Asymptote horizontale.
LIMITES DE FONCTIONS - INTERPRÉTATION GRAPHIQUE
Exercice 1 (Lecture graphique de limites). Dans chacun des cas suivants on donne la représentation graphique d'une fonction f.
Matheleve
Soit la représentation graphique d'une fonction f dans un repère orthogonal Interpréter graphiquement
Dérivée dune fonction et interprétation graphique
Il s'agit donc de la droite passant par M0 (x0f (x0)) et de coefficient directeur l. On notera alors f (x0) cette limite c'est à dire : f (x) ? f (x0).
exercice-limite-graphique.pdf
Conjecturer limite et asymptote graphiquement. On consid`ere les fonctions /1 /2
1 LIMITES I Limites en linfini 1°) Limites infinies en linfini Exemple
Remarque : l'interprétation graphique de cette limite est que la courbe de f admet l'axe des abscisses d'équation y=0 comme asymptote horizontale. Exemple 2: d°
Limites de fonctions – Comportement asymptotique - Exercices
Donner une interprétation graphique de chacune de ces limites. Exercice 3 corrigé disponible. Déterminer les limites suivantes :.
Concordance entre deux méthodes de mesure dune même variable
12 nov. 2015 en incorporant le biais dans l'interprétation. D. Biais = 23 – limites de concordance = ±37. Limites de concordance larges
Les limites
10 ? Chapitre 1. Les limites. A. Interprétation graphique. Pour les questions suivantes on considère le graphe ci-dessous où ont été.
Exemples de limites dune fonction en un réel. Interprétation graphique
Exemples de limites d'une fonction en un réel. Interprétation graphique. Définition. Soit a un nombre réel. On dit que le réel x tend vers a et on note x.
LIMITES DES FONCTIONS - maths et tiques
Méthode : Déterminer graphiquement des limites d'une fonction Vidéo https://youtu be/9nEJCL3s2eU On donne ci-dessous la représentation graphique de la fonction " a) Lire graphiquement les limites en ?? en +? en ?4 et en 5 b) Compléter alors le tableau de variations de "
Graphologie : ce que votre écriture révèle de vous - Doctissimo
On a donc par produit des limites lim x?+? x3 ?3x2 +4x+1 = +? vu comme 1×+? ?? A faire en TD : cas des polynômes et des fractions rationnelles IV Interprétation graphique et asymptotes 1) Asymptote horizontale Si lim x?+? f(x) = l pour M et P les points d’abscisses x lorsque x prend des valeurs de plus en plus
Interpretation graphique des limites - labmathfesecbe
Esquisser les graphiques de fonctions répondant à des conditions sur les limites (asymptotes verticales et/ou horizontales) Partie 3 Traduire en termes de limites des comportements de fonctions autour d'un réel où elle n'est pas définie
Terminale générale - Limites de fonctions - Exercices - Devoirs
Dans chacun des cas suivants on donne la représentation graphique d’une fonction f ainsi que les éventuelles asymptotes En déduire : - le domaine de définition de f - les limites aux bornes de l’ensemble de définition Exercice 2 corrigé disponible
1 Limites en un réel a Interprétation graphique
Calcul de limites 1 Limites en un réel a Interprétation graphique Etudier la limite de la fonction au point f a dans les cas suivantset interpréter les résultats On distinguera éventuellement la limite à gauche et la limite à droite (1) fx x x x 32 7 91 1 a 1 2 2 (2) fx x x 2 2 5 a 2 6 10
Searches related to interpretation graphique des limites PDF
4 Interprétation graphique LIMITES EN UN REEL – INTERPRETATION GRAPHIQUE https://bit ly/3amk769 Trois cas peuvent se présenter dans le calcul de limite en un réel : • IMAGE Lorsque le calcul de limite d’une fonction en un réel donne immédiatement un nombre : lim x a f x b ? = cela signifie que l’image de a est b
Quels sont les limites de la graphologie ?
Delphine Maison note cependant d’autres limites de la graphologie, comme par exemple le fait de ne pas pouvoir dire si l’écriture est celle d’une femme ou d’un homme - il serait en effet faux et extrêmement stéréotypé de penser qu’une écriture soit plus masculine ou féminine selon son degré de lisibilité, par exemple. De même pour l’âge.
Comment interpréter une limite ?
Une limite s'interpréte graphiquement avec l'existence éventuelle d'asymptotes ou de directions asymptotiques. Soit f et g deux fonctions et a et b deux réels fixés. dans ces cas on dit que la droite d'équation x = a est asymptote à la courbe représentative de f.
Comment définir les limites ?
De la sorte, les limites sont définies par les exclusions hors de la cité, et imposent des frontières, c’est-à-dire des limites, de limites, ce qui borne un terrain, un territoire, chemin bordant un domaine, sentier entre deux champs.
Comment calculer les limites infinies?
Autrement dit : lim x?a (g?f(x)) = lim y?limaf(x) g(y). Théorème 11.2.24 (Opérations sur des limites in?nies) Les règles précédentes restent vraies (avec les règles opératoires de R) dans toutes les situations n’a- menant pas une des formes indéterminées suivantes : 0×?, ???, ? ? , 0 0 .
BL | 1
e& 2eannéeChapitre | AN08 Dérivée d"une fonction et interprétation graphiqueVersion du 10-08-2023 à 11:39
1.Notion de tangente en un point du grapheContexte
Dans ce paragraphe, et sauf mention contraire,Idésignera un intervalle deR, non vide et non réduit à un point,x0un
élément deIetf:I7-→Rune fonction de la variable réelle.Définition 1| Limite du taux d"accroissement
xf(x)M0f(x0)x
0Mf(x)xxf(x)M
0f(x0)x
0Mf(x)xxf(x)M
0f(x0)x
0Mf(x)x
xf(x)M0f(x0)x
0Mf(x)xxf(x)M
0f(x0)x
0Mf(x)xxf(x)M
0f(x0)x
0Mf(x)x
Ladroite(M0M), oùM(x,f(x))etM0(x0,f(x0))a pour coefficient directeurf(x)-f(x0)x-x0.Sif(x)-f(x0)x-x0-→x→x0ℓavecℓréel fini,alors, la droite (M0M)tend vers une droite non verticale, que l"on appelle
alorstangente à la courbe représentative defenx0.Il s"agit donc de ladroite passant parM0(x0,f(x0))et decoefficient directeurℓ.On notera alorsf′(x0)cette limite c"est à dire :f(x)-f(x0)x-x0-→x→x0f′(x0)Graphiquement, cela signifie que le pointMse rapproche du pointM0. La tangente est ainsi la " droite limite » ainsi
obtenue.Équation de la tangente àCfOn suppose quef(x)-f(x0)x-x0-→x→x0ℓ=f′(x0)réel fini.LatangenteàCfau point d"abscissex0est la droite passant par le pointM0(x0,f(x0))eta pour
équation:
y=f′(x0)(x-x0) +f(x0)CPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 11:391AN08| Dérivée d"une fonction et interprétation graphiqueBL | 1
e& 2eannéeDéfinition 2| Dérivabilité enx0On dira quefest dérivable enx0lorsquelim h→0f(x0+h)-f(x0)hexisteet estréelle. Lorsque c"est le cas, cette limite s"appelle lenombre dérivé defenx0, et on noteraf ′(x0)la valeur de cette limite, c"està dire :f(x0+h)-f(x0)h
-→h→0f′(x0)En notanth=x-x0, cette définition est équivalente à la suivante :fest dérivable enx0lorsquelim
x→x0f(x)-f(x0)x-x0existeet estréelle.Définition 3| Tangente horizonaleLorsque
f(x)-f(x0)x-x0-→x→x00c"est à diref′(x0) = 0, la tangente àCfenx0estparallèle à l"axe
des abscisses, c"est à dire est horizontale, et a pour équationy=f(x0).Exemple de positions possibles
Dans ce casCfpeut ou non traverser sa tangente comme par exemple :xf(x)f(x0)x0xf(x)f(x0)x
0xf(x)f(x0)x
0Définition 4| Tangente verticale
Lorsquef(x)-f(x0)x-x0-→x→x0+∞ou-∞, on dira que la courbe représentative defprésente au pointx0unetangente verticalequi a pour équation x=x0. xf(x)Illustration de cette " verticalisation » xf(x)x 0M0Mf(x)xxf(x)x
0M0Mf(x)xxf(x)x
0M0Mf(x)x
Exemple usuel
d"équationx= 0.CPGE-BL | 1
e& 2eannée|Mathématiques Version du 10-08-2023 à 11:392AN08| Dérivée d"une fonction et interprétation graphiqueBL | 1
e& 2eannée2.Tangente à gauche et à droiteRemarque 1| Taux d"accroissement à gauche et à droite différents
Lorsque l"on détermine la limite enx0def(x0+h)-f(x0)h , on est parfois amené à distinguer le calcul de la limite àgauche en0et de la limite à droite en0pour ce taux d"accroissement.On obtient parfoispour ces deux limites des valeurs différentes, qu"il conviendra d"interprêter comme sur
les deux exemples ci-dessous.xf(x)f(x0)x0f(x)-f(x0)x-x0-→
x→x+0+∞maisf(x)-f(x0)x-x0-→
x→x-0ℓ∈Rxf(x)f(x0)x
0f(x)-f(x0)x-x0-→
x→x+0ℓ
1∈Rmaisf(x)-f(x0)x-x0-→
x→x-0ℓ
2∈R
avecℓ1̸=ℓ2Définition 5| Dérivabilité à droite On suppose ici quex0̸= sup(I).On dit quefestdérivable à droite enx0lorsque la restrictiondefà l"intervalleI∩[x0;+∞[estdéri- vableenx0c"est à dire : f(x0+h)-f(x0)h0Lademi-tangente à droiteTdàCfenx0est la demi-droite d"équation :Td:y=f′d(x0)(x-x0) +f(x0)
x≥x0Dérivabilité à gaucheOn suppose ici quex0̸= inf(I).
On dit quefestdérivable à gauche enx0lorsque larestrictiondefà l"intervalle]-∞;x0]∩Iestdérivableenx0
c"est à dire :f(x0+h)-f(x0)h et on peut ainsi définir la notion dedemi-tangente à gauche enx0.Demi-tangente verticaleOn rappelle que si
f(x0+h)-f(x0)h -→h→0+∞ou-∞, alors la fonction n"est pas dérivable enx0, etCfprésente en ce point une tangente verticale. Cette définition s"étend ainsi à la notion de dérivée à droite ou à gauche, où l"on parlera dedemi-tangente verticale à droiteouà gauche.xf(x)f(x0)x0CPGE-BL | 1
e& 2eannée|Mathématiques Version du 10-08-2023 à 11:393AN08| Dérivée d"une fonction et interprétation graphiqueBL | 1
e& 2eannée3.Fonctions dérivablesContexteDans ce paragraphe, et sauf mention contraire,Idésignera un intervalle deR, non vide et non réduit à un point,x0un
élément deIetf:I7-→Rune fonction de la variable réelle.Définition 6| Dérivabilité en un point et fonction dérivable et fonction dérivée
Dérivabilité en un pointx0On dit quefest dérivable enx0∈Ilorsque letaux d"accroissementf(x)-f(x0)x-x0defenx0a une limite finieen
x 0. On note alorsf′(x0)cette limite, c"est à dire :f(x)-f(x0)x-x0-→ x→x0f′(x0) Le nombref′(x0)est appelénombre dérivé defenx0.On rappelle que l"on a une définition analogue en utilisant la limite en0du quotientf(x0+h)-f(x0)h
.Fonction dérivéeOn appelle alorsdérivée defoufonction dérivée def, l"application qui, à chaquex∈Itel
quef′(x)existe, associef′(x). Si l"on note∆f={x∈I, f′(x)existe}, on a ainsi :f′:∆ f-→Rx7-→f′(x)Remarque 2| Autre expression et notationsLa notion de dérivée en un point est une notion locale: on regarde en effet le comportement du quotient
f(x0+h)-f(x0)h pourhau voisinage de0.Le nombref′(x0)est parfois notédfdx(x0)ouDf(x0).Proposition 1| Calculs de dérivées et opérations sur les dérivées
Dérivée d"une combinaison linéaire
Soientf:I-→R,g:I-→Retx0∈I, etλ∈R∗.Sifetgsont dérivables enx0,alorsf+getλfle sont, et on a :
(f+g)′(x0) =f′(x0) +g′(x0)et(λf)′(x0) =λf′(x0)f+g⇝se dérive enf′+g′λf⇝se dérive enλf′Dérivée d"un produit
Soientf:I-→R,g:I-→Retx0∈I.Sifetgsont dérivables enx0,alorsfgetλfle sont, et on a :(fg)′(x0) =f′(x0)g(x0) +f(x0)g′(x0)f×g⇝se dérive enf′×g+f×g′CPGE-BL | 1
e& 2eannée|Mathématiques Version du 10-08-2023 à 11:394AN08| Dérivée d"une fonction et interprétation graphiqueBL | 1
e& 2eannéeDérivée d"une composée IetJdésignent deux intervalles non vides non réduitsà un point deR.
Soitf:I-→R,g:J-→Rtel quef(I)⊂J, et
x0∈I.Sifest dérivable enx0et sigest dérivable en
f(x0),alorsg◦fest dérivable enx0, et :(g◦f)′(x0) =f′(x0)×g′(f(x0))g◦f⇝se dérive enf′×(g′◦f)Dérivé de l"inverse
Soitf:I-→Rtelle que que, pour toutx∈I,
f(x)̸= 0, etx0∈I.Sifest dérivable enx0,alors 1f est définie surIet est dérivable enx0, et : 1f (x0) =-f′(x0)(f(x0))21 f ⇝se dérive en-f′f2Dérivé d"un quotient
Soitf:I-→R,g:I-→Rtelle que pour tout
x∈I,g(x)̸= 0, etx0∈I.Sifetgsont dérivables enx0,alors fg est définie surIet est dérivable surI, et : fg (x0) =f′(x0)g(x0)-f(x0)g′(x0)(g(x0))2f g ⇝se dérive enf ′×g-f×g′g2Dérivée de la fonction réciproque
Soitf:I-→Rcontinue et strictement monotone
surI. Alorsfréalise une bijection deIsur l"intervalleJ= f(I). On noteg=f-1sa bijection réciproque. Soitx0∈J.Sifest dérivable ent0=g(x0)etf′(t0)̸= 0,alorsgest dérivable enx0et :g ′(x0) =1f ′(t0)=1f ′(g(x0))f -1⇝se dérive en1f ′◦f-1Proposition 2| Dérivée des fonctions usuellesDans cet encart,udésigne une fonction définie sur un intervalleIdeRde sorte que les composées
écrites ci-dessous soient définies et dérivables.Puissances pourn∈Zx n⇝se dérive ennxn-1u n⇝se dérive enu′×nun-1Exponentielle e x⇝se dérive enexe u⇝se dérive enu′×euPuissances pourα∈Rxα⇝se dérive enαxα-1u
α⇝se dérive enu′×αuα-1Logarithme ln(x)⇝se dérive en1x ln(u)⇝se dérive enu′×1uCosinus cos(x)⇝se dérive en-sin(x)cos(u)⇝se dérive en-u′×sin(u)Sinus sin(x)⇝se dérive encos(x)sin(u)⇝se dérive enu′×cos(u)CPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 11:395AN08| Dérivée d"une fonction et interprétation graphiqueBL | 1
e& 2eannéeTangente tan(x)⇝se dérive en1 + tan2(x) =1cos2(x)tan(u)⇝se dérive enu′×1 + tan2(u)=u′×1cos
2(u)Arctangente
arctan(x)⇝se dérive en11 +x2arctan(u)⇝se dérive enu′×11 +u24.Lien entre dérivabilité à gauche et à droite et dérivabilitéDéfinition 7| Notion d"intérieur d"un intervalle et dérivabilité
On note
◦Il"ensemble des points deIdistincts des bornes, on l"appelleintérieur deI.IllustrationPourI= [-3;4], on
a : ◦I=..............PourI= [-3;4[, on a : ◦I=..............PourI= ]-3;4], on a : ◦I=..............PourI= ]-∞;4], on a :◦I=..............Dérivabilité sur un intervalleIEn fait, quand on ditfest dérivable surIc"est que :
fest dérivable en tout point de l"intérieur deI, fest dérivable à gauche ensup(I)sisup(I)∈I,fest dérivable à droite eninf(I)siinf(I)∈I.Théorème 1| Dérivabilité en un point intérieur àIOn suppose quex0∈◦I.(fest dérivable enx0)⇔
festdérivable à gauche et à droiteenx0 Lorsque c"est le cas, on a :f ′(x0) =f′d(x0) =f′g(x0).CPGE-BL | 1
e& 2eannée|Mathématiques Version du 10-08-2023 à 11:396AN08| Dérivée d"une fonction et interprétation graphiqueBL | 1
e& 2eannéeDéfinition 8| Point anguleuxEn un pointM(x0,f(x0))avecx0∈◦Isif
′d(x0)̸= f ′g(x0)(sous réserve qu"elles existent), on dit queM est un point anguleux. xf(x)f(x0)x0Cas classique de point anguleux : la valeur absolue
La fonctionx7-→ |x|présente en0un point angu- leux.En effet, puisque :
∀x∈R,|x|=xsix≥0 -xsix <0 on en déduit que son nombre dérivé à droite vaut1,alors que son nombre dérivé à gauche vaut-1.xf(x)La fonctionx7-→ |x|n"est donc pas dérivable en0.
5.Lien continuité et dérivabilitéThéorème 2| Continuité et dérivabilité
Sifestdérivableenx0(resp. à droite, à gauche),alorsfestcontinueenx0(resp. à droite, à gauche).Réciproque fausse
La fonction valeur absolue est continue en0, mais n"est pas dérivable en0.Une fonction continue présentant un point anguleux n"est pas dérivable en ce point.Contraposée du résultat
Sifn"est pas continue enx0,alorsfn"est pas dérivable enx0.En d"autres termes, on n"ira pas regarder la dérivibalité d"une fonction en un point où elle n"est pas
continue.CPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 11:397AN08| Dérivée d"une fonction et interprétation graphiqueBL | 1
e& 2eannée6.Définition de la dérivabilité par développement limitéContexte Dans tout ce qui suit, sauf mention spécifique : Idésignera un intervalle non vide non réduit à un point, et(a,b)∈R2aveca < b; fsera une fonction définie surIà valeurs dansR, c"est à diref:I-→Rx7-→f(x); x0est un élément deI.Définition 9| Développement limité d"ordre 1 xf(x)C fT:y=f′(x0)(x-x0) +f(x0)f(x0)x0x•
Écart entreCfetT:
(x-x0)×ε(x-x0)festdérivableenx0si, et seulement si, il existeℓ∈Ret unefonctionε:V0-→Rdéfinie sur un voisinageV0de0 telle que : ∀h∈V0, f(x0+h) =f(x0) +ℓ|{z} =f′(x0)×h+h×ε(h)avecε(h)-→h→00En revenant àxen posanth=x-x0et en notantVx0un voisinage dex0, vient alors :
∀x∈Vx0, f(x) =f(x0) +f′(x0)(x-x0)|{z}Équation de la tangenteTà
Cfau point d"abscissex0+(x-x0)×ε(x-x0)avecε(x-x0)-→x→x00Cette dernière expression est appellée développement limité d"ordre 1 pourfenx0.CPGE-BL | 1
e& 2eannée|Mathématiques Version du 10-08-2023 à 11:398AN08| Dérivée d"une fonction et interprétation graphiquequotesdbs_dbs45.pdfusesText_45[PDF] interpretation graphique d'une inequation
[PDF] convexité d'une fonction
[PDF] interpréter graphiquement une limite
[PDF] donner une interprétation graphique d'une suite
[PDF] concave convexe anatomie
[PDF] valeurs relatives au travail
[PDF] valeurs de travail
[PDF] l avare séquence pédagogique
[PDF] point d'intérêt d'une image
[PDF] harris detector
[PDF] détecteur de harris algorithme
[PDF] algorithme de detection de contour d'une image
[PDF] détecteur de harris matlab
[PDF] detection des contours d'une image
