 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
x ↦→ arctan(tanx). Correction ▽. [005084]. Exercice 2 ***IT. 1. Calculer arccosx+arcsinx pour
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Séries
Séries
est divergente et donc la série de terme général un diverge. 8. ln. ( 2 π arctan. (n2 +1 n. )).
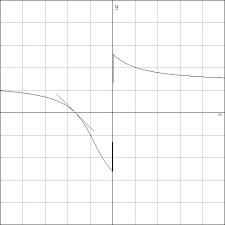 Sans titre
Sans titre
1 + x x. = 1 on obtient que lim x→±∞ f(x) = arctan(1) = π. 4. – Calcul des limites en 0 : par composition on obtient : lim x→0− f(x) = − π. 2 lim x→0+ f
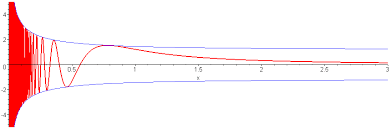 TD 1 Intégrales généralisées
TD 1 Intégrales généralisées
16 sept. 2016 )1²)(1(t t dt. = ... = ln. ²1. 1 t t. +. +. + Arctan t. +∞. 0. = 2 π . Variante : le changement de variable t = x x. −1 donne le même résultat ...
 AP 07 Calculus BC Form B Q2
AP 07 Calculus BC Form B Q2
arctan. 1 dx t dt t. = + and. (. ) 2 ln. 1 dy t dt. = + for. At time the object is 1 point in part (c) and 2 points in part (d). Correct work is presented in ...
 Sia x > 0; risulta allora arctanx + arctan(1/x) = π/2
Sia x > 0; risulta allora arctanx + arctan(1/x) = π/2
Dimostrazione. Osserviamo preliminarmente che come risulta dalla definizione della funzione ar- cotangente
 UVSQ / L1 S2 LSMA202N Mathématiques générales 2 Feuille de
UVSQ / L1 S2 LSMA202N Mathématiques générales 2 Feuille de
Chacune des fonctions 2شey ≠ 1 et 2 arctan. شey ≠ 1 est définie pour y > 0 mais n'est dérivable que pour y > 0. Cependant on peut vérifier que la fonction
 [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
cours du mercredi 1/3/17 Chapitre V Fonctions arcsin arccos arctan 1 Définitions 1 1 arcsin Proposition 1 1 La fonction sin : [??/2 ?/2] ? [?11]
 [PDF] 254 Compléments (fonctions trigonométriques inverses)
[PDF] 254 Compléments (fonctions trigonométriques inverses)
1 Le domaine de définition de arctan est R 2 y = arctan(x) (tan(y) = x et ? ? 2
 [PDF] fic00082pdf - Exo7 - Exercices de mathématiques
[PDF] fic00082pdf - Exo7 - Exercices de mathématiques
x ?? arctan(tanx) Correction ? [005084] Exercice 2 ***IT 1 Calculer arccosx+arcsinx pour
 [PDF] arctan(1) + arctan(2) + arctan(3) = ?
[PDF] arctan(1) + arctan(2) + arctan(3) = ?
Page 1 = arctan(1) + arctan(2) + arctan(3) ?
 [PDF] dspArctanpdf - Math et info
[PDF] dspArctanpdf - Math et info
Page 1 Somme d'arctangentes arctan(1) + arctan(2) + arctan (3) = ?
 [PDF] CM4-transpdf - Cours de Mathématiques L1 Semestre 1
[PDF] CM4-transpdf - Cours de Mathématiques L1 Semestre 1
cos : R ? [-11] n'est pas une bijection Mais cos : [0?] ? [-11] est continue et strictement décroissante Sur arctan(tan(x)) = x Vx ? ]-?
 [PDF] La fonction Arctangente
[PDF] La fonction Arctangente
La fonction Arctangente I Rappels sur la fonction tangente 1°) Définition sin tan cos x x x = tan x existe pour tout réel x qui n'est pas de la forme
 [PDF] 1 Convergence et somme des séries : ? arctan 1 n2 + 3n + 3 ? 3n
[PDF] 1 Convergence et somme des séries : ? arctan 1 n2 + 3n + 3 ? 3n
sn est une somme partielle télescopique : sn = vn ? v?1 = arctan n + 2 ? arctan 1 (sn) a une limite S = ?/4 donc ? un est convergente de somme S
 [PDF] Tableaux des dérivées et primitives et quelques formules en prime
[PDF] Tableaux des dérivées et primitives et quelques formules en prime
%2520d%25C3%25A9riv%25C3%25A9es
 [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
On note arccos : [?11] ? [0?] la fonction réciproque i e si ?1 ? x ? 1 alors y = arccosx ? cosy = x ET 0 ? x ? ? 1 3 arctan
 [PDF] La fonction Arctangente
[PDF] La fonction Arctangente
La courbe de la fonction « tangente » ressemble à un électrocardiogramme On vérifie le tracé sur la calculatrice graphique Page 2 II Généralités 1
 [PDF] [PDF] Exo7 - Exercices de mathématiques
[PDF] [PDF] Exo7 - Exercices de mathématiques
Calculer arccosx+arcsinx pour x élément de [?11] 2 Calculer arctanx+arctan 1 x pour x réel non nul 3 Calculer cos(arctana) et sin(arctana) pour a réel
 [PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
[PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
%2520d%25C3%25A9riv%25C3%25A9es
 [PDF] 254 Compléments (fonctions trigonométriques inverses)
[PDF] 254 Compléments (fonctions trigonométriques inverses)
arctan est dérivable sur R et on a arctan(x)' = 1 1 + x2 IV Complément à la liste des primitives des fonctions usuelles: ? désignant une constante réelle
 [PDF] I Propriétés fondamentales - Normale Sup
[PDF] I Propriétés fondamentales - Normale Sup
Le graphe de f?1 est le symétrique du graphe de f par rapport à la droite y = x III 2 Les fonctions arccos arcsin arctan (a) La fonction x ?? cosx induit
 [PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
[PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
Trouvons une fonction réciproque de cos D'abord cos : R ? [-11] n'est pas une bijection Mais cos : [0?] ? [-11] est continue et strictement
 [PDF] Formulaire de trigonométrie 1 Fonctions trigonométriques - LPSM
[PDF] Formulaire de trigonométrie 1 Fonctions trigonométriques - LPSM
] Ces trois fonctions vérifient les formules suivantes : arccos(x) + arcsin(x) = ? 2 arctan
 [PDF] Université de Provence
[PDF] Université de Provence
1 tan ( arctan(b) ) = cotan( arctan(b)) = tan (? 2 ? arctan(b)) Or a Soit la fonction f définie par f(x) = arctan ?1?sin x 1+sin x
Comment calculer arctan de 1 ?
La valeur exacte de arctan(?1) est ??4 .Quelle est la valeur exacte d'Arctan 1 ?
Quelle est la valeur d'Arctan 1 ? La valeur de arctan 1 ou tan inverse 1 est égale à ?/4 radians ou 45 degrés .Quel est la valeur de arctan ?
La règle de la fonction arc tangente de base est f(x)=arctan(x). f ( x ) = arctan ? On note aussi cette fonction f(x)=tan?1(x). f ( x ) = tan ? 1 ?- La fonction arcsin est impaire. Elle est dérivable sur ]?1,1[ et sa dérivée est donnée par, pour tout x?]?1,1[, x ? ] ? 1 , 1 [ , (arcsin)?(x)=1?1?x2. ( arcsin ) ? ( x ) = 1 1 ? x 2 . Il faut faire attention au fait que la fonction arcsin est la réciproque de la restriction de sin à l'intervalle [??/2,?/2].
Analyse (2) : Séries numériques
Les incontournables :
1. Convergence et somme des séries :?arctan1n
2+ 3n+ 3?3n-1sin3α3
n.D1-17 (a) - ?u nest une SATP (série à termes dansR+). -arctant≂t→0tdoncun≂1n2+ 3n+ 3≂1n
2, ce qui est le TG (terme général) d"une série
de Riemann convergente.Par thm de comparaison,?u
nest convergente.Ou bien directement :
s n=n? k=0u ketuk= arctantanvk-tanvk-11 + tanvktanvk-1= arctan(tan(vk-vk-1))en notantk+2 = tanvk. k+ 2?R+donc on peut choisirvk?[0,π/2[et alorsvk-vk-1?]-π/2,π/2[(en fait ?[0,π/2[) doncuk=vk-vk-1. s nest une somme partielle télescopique :sn=vn-v-1= arctann+ 2-arctan1. (sn)a une limiteS=π/4donc?u nest convergente de sommeS. (b) ?|un|est une SATP. sint≂t→0tdoncun≂ 3n-1? α3 n?3=O((19
)n)qui est le TG d"une série géométrique conver- gente.Par thm de comparaison,?u
nest absolument convergente.Ou bien directement :
s n=n? k=0u ketuk= 3k-1?14 (3sinα3 k-sin3α3 k)? =143ksinα3
k-3k-1sinα3 k-1)? s nest télescopique :sn=143nsinα3
n-3-1sinα3 -1)? sin α3 n≂α3 ndonc(sn)a une limiteS=14 (α-sin3α3 )donc?u nest convergente de sommeS.2. Etudier
?nlnn(lnn)n??lnnn3?1⎷nlnn?
1n(lnn)2.
Valeur approchée à10-2près de+∞?
n=21n(lnn)2. (a) ?u nest une SATP. lnun= (lnn)2-nlnlnn≂ -nlnlnndonc il existen0?Ntel quelnun-nlnlnn≥1/2si n≥n0. Soit un teln0. uPar thm de comparaison,?u
nest convergente. (b) ?u nest une SATP. (lnn)3=o(n)doncun=o?1n 2? ce qui est le TG d"une série de Riemann convergente.Par thm de comparaison,
?u nest convergente.(C"est une série de Bertrand?1nα(lnn)β
avecα >1) (c)?u nest une SATP. lnn=o(n)donc1n =o(un)et1n est le TG d"une série de Riemann divergente.Par thm de comparaison,
?u nest divergente.(C"est une série de Bertrand?1nα(lnn)β
avecα <1) Exercices de Mathématiques PC - Mathilde PETIT - 2011Analyse (2) : Séries numériques
(d) ?u nest une SATP. n n-1φ=vn sin≥3ettn=n? k=3v k=? n 2φ=1ln2
-1lnnest le TG d"une suite qui a une limite (1ln2 donc ?v nest une série convergente.Par thm de comparaison,
?u nest convergente.(C"est une série de Bertrand?1nα(lnn)β
avecα= 1etβ >1)Pour toutn≥2,sn=n?
k=2u kest une valeur approchée de la sommeSetrn=+∞? k=n+1u k=S-sn. n très lente), alorsS=sn+ 0,01à0,01près.3. Etudier la série
?arccos?2π arctann2? .d1-016 ?u nest une SATP.Soitcn=2π
arctann2.limcn= 1donclimun= 0etun≂sinun=?1-c2n=?2 2 -arctann2. π2 -arctann2= arctan1n2≂1n
2doncun≂?2
1n ce qui est le TG d"une série (harmonique) divergente.Par thm de comparaison,?u
nest divergente.4. Prouver que
?(-1)nlnnn est semi-convergente et donner une valeur approchée à10-3près de sa somme. ?u nest une série alternée. -t?→lntt estC1sur[1,+∞[de dérivéet?→1-lntt2négative sur[3,+∞[donc(|un|)n≥3
décroit. -limun= 0. D"après le TSSA (thm des séries alternées),?u nest convergente.Mais|un| ≥1n
sin≥3et1n est le TG d"une série divergente donc?|un|est divergente ie?u nest semi-convergente.D"après le TSSA, sin≥3, alorsrn=+∞?
k=n+1uà0,001près.
5. Etudier la série
??(n+1)π nπ e-⎷x sinxdx.d1-042 t?→x=nπ+testC1de[0,π]sur[nπ,(n+ 1)π]doncun= (-1)n? 0 e-⎷nπ+tsintdtest leTG d"une série alternée.
|un|=? 0 e-⎷nπ+tsintdt≥? 0 e-⎷(n+1)π+tsintdt=|un+1|ie(|un|)est une suite décrois- sante. 0 e-⎷nπ dt=πe-⎷nπ donclimun= 0. Exercices de Mathématiques PC - Mathilde PETIT - 2011Analyse (2) : Séries numériques
D"après le TSSA,
?u nest une série convergente. e -⎷nπ =O(?1⎷nπ 3 ) =O(1n3/2)donc la convergence est absolue.
6. Etudier la série de terme généralun=3?n
6+n4+n2-1-?n
4+an2+bn+ 1pour
(a,b)?R2.d1-066 3 ?n6+n4+n2-1 =n2(1 +t)1/3oùt=1n
2+1n 4-1n6≂1n
2.On a donc
3?n6+n4+n2-1 =n2(1 +13
t-19 t2+o(t2)) =n2+13 +29n2+o(1/n2).De même,
?n4+an2+bn+ 1 =n2+a2
+b2n+4-a8n2+o(1/n2)d"oùun=2-3a6 -b2n+O(1/n2).Sia?= 2/3, alorsun≂2-3a6
donc(limun= 0)est faux :?u nest grossièrement divergente.Sia= 2/3etb?= 0, alorsun≂-bn
donc?u nest à termes réels de signe constant pourn≥n0 et ?1n est divergente donc, par comparaison,?u nest divergente.Sia= 2/3etb= 0, alors|un|=O(1/n2)donc?u
nest absolument convergente.7. Etudier la série
?cos(π?n2+n+ 2).d1-006
?n2+n+ 2 =n(1+12n+78n2-716n3+o(1/n3))doncun= cos(nπ+π/2+t)oùt≂7π8ndonc
u n= (-1)n+1sint= (-1)n+1(t-t36 +o(1/n3)) = (-1)n+17π8n+O(1/n2). v n=-7π8 (-1)nn est le TG d"une série semi-convergente. w n=O(1/n2)est le TG d"une série absolument convergente.?u nest donc semi-convergente.8. Prouver que le produit de Cauchy de 2 séries exponentielles est une série exponentielle.
Valeur approchée à10-5près deexp(1/3).
Soit?u
n=?xnn!,?v n=?ynn!et?w nleur produit de Cauchy. w n=n? k=0u kvn-k=n? k=0x kyn-kk!(n-k)!=1n!n k=0? n k? x kyn-k=(x+y)nn!ce qui est le TG d"une série exponentielle. exp(1/3) =sn+rnoùsn=n? k=0a ketrn=+∞? k=n+1a kavecak=13 kk!.Sik≥n, alorsak=an13
k-n(n+ 1)k-n=α(3(n+ 1))koùα=an3n(n+1)n ne dépend pas dek, etbk=?13(n+ 1)? k est le TG d"une série géométrique convergente donc13(n+1)?
n+11-13(n+1)=1(3n+ 2)3nn!.9. Prouver que la suite(?
n? 11k -lnn)est convergente.(Sa limite s"appelle la "constante d"Euler")Soitun=?
n? 11kAlors?n≥1, un=n?
k=1a ket on étudie la série?a n. Exercices de Mathématiques PC - Mathilde PETIT - 2011Analyse (2) : Séries numériques
a n=1n + ln(1-1n ) =-12n2+o(1/n2) =O(1/n2)donc?a nest absolument convergente. La suite(un)a donc une limite.10. Convergence et somme de la série de terme général
2n3-3n2+ 1(n+ 3)!.d1-106
P(n) = 2n3-3n2+1 =a(n+3)(n+2)(n+1)+b(n+3)(n+2)+c(n+3)+deta= 2,b=-15,c= 53,d=-80. u n=an!+b(n+ 1)!+c(n+ 2)!+d(n+ 3)!donc?u nest la somme de4séries convergentes. n=0u n=a+∞? n=01n!+b+∞? n=11n!+c+∞? n=21n!+d+∞? n=31n!=ae+b(e-1)+c(e-2)+d(e-5/2) = 109-40e.11. On admet que
n=11n2=π26
. Calculer+∞? n=01(2n+ 1)2et+∞? n=1(-1)nn 2. n k=01(2k+ 1)2=2n+1? k=11k 2-n? k=11(2k)2=s2n+1-14 snoù(sn)est la suite des sommes partielles de la série (convergente de sommeS=π26 )?1n2donc+∞?
n=01(2n+ 1)2existe et vautS-14S=π28
n k=1(-1)kk 2+n? k=11k 2= 2? s[n/2]doncn? k=1(-1)kk 2=12 s[n/2]-sndonc+∞? n=1(-1)nn 2 existe et vaut 12S-S=-π212
.Pour aller plus loin :12. Pourn≥2, on posean=(-1)n⎷n
, bn=(-1)n⎷n+ (-1)n, cn=(-1)n?n+ (-1)n; étudier les séries?aquotesdbs_dbs45.pdfusesText_45[PDF] equivalent de arctan en l'infini
[PDF] tangente hyperbolique dérivée
[PDF] tableau de conjugaison ce2
[PDF] lettre de motivation sorbonne licence
[PDF] fonction hyperbolique exo7
[PDF] dérivée cosh
[PDF] lettre de motivation stage immobilier débutant
[PDF] les fonctions hyperboliques et leurs réciproques pdf
[PDF] trigo hyperbolique
[PDF] lettre de motivation agence immobilière sans experience
[PDF] up and down tome 4
[PDF] ch(2x)
[PDF] up and down saison 4 pdf
[PDF] up and down saison 2 pdf ekladata
