[PDF] [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés





Previous PDF Next PDF



Chapitre V Fonctions arcsin arccos

http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf



Exercices de mathématiques - Exo7

x ↦→ arctan(tanx). Correction ▽. [005084]. Exercice 2 ***IT. 1. Calculer arccosx+arcsinx pour 





Séries

est divergente et donc la série de terme général un diverge. 8. ln. ( 2 π arctan. (n2 +1 n. )).



Analyse (2) : Séries numériques Les incontournables : 1

uk et uk = arctan tan vk − tan vk−1. 1 + tan vk tan vk−1. = arctan(tan(vk−vk−1)) en notant k+2 = tan vk. k + 2 ∈ R+ donc on peut choisir vk ∈ [0 π/2[ et 



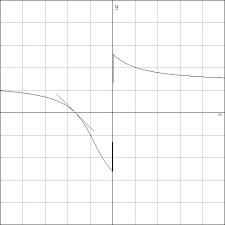Sans titre Sans titre

1 + x x. = 1 on obtient que lim x→±∞ f(x) = arctan(1) = π. 4. – Calcul des limites en 0 : par composition on obtient : lim x→0− f(x) = − π. 2 lim x→0+ f 



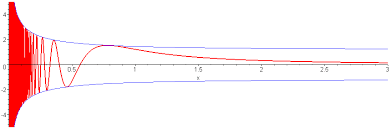TD 1 Intégrales généralisées TD 1 Intégrales généralisées

16 sept. 2016 )1²)(1(t t dt. = ... = ln. ²1. 1 t t. +. +. + Arctan t. +∞. 0. = 2 π . Variante : le changement de variable t = x x. −1 donne le même résultat ...



AP 07 Calculus BC Form B Q2 AP 07 Calculus BC Form B Q2

arctan. 1 dx t dt t. = + and. (. ) 2 ln. 1 dy t dt. = + for. At time the object is 1 point in part (c) and 2 points in part (d). Correct work is presented in ...



Sia x > 0; risulta allora arctanx + arctan(1/x) = π/2

Dimostrazione. Osserviamo preliminarmente che come risulta dalla definizione della funzione ar- cotangente



UVSQ / L1 S2 LSMA202N Mathématiques générales 2 Feuille de

Chacune des fonctions 2شey ≠ 1 et 2 arctan. شey ≠ 1 est définie pour y > 0 mais n'est dérivable que pour y > 0. Cependant on peut vérifier que la fonction 



[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés

cours du mercredi 1/3/17 Chapitre V Fonctions arcsin arccos arctan 1 Définitions 1 1 arcsin Proposition 1 1 La fonction sin : [??/2 ?/2] ? [?11] 



[PDF] 254 Compléments (fonctions trigonométriques inverses)

1 Le domaine de définition de arctan est R 2 y = arctan(x) (tan(y) = x et ? ? 2



[PDF] fic00082pdf - Exo7 - Exercices de mathématiques

x ?? arctan(tanx) Correction ? [005084] Exercice 2 ***IT 1 Calculer arccosx+arcsinx pour 



[PDF] arctan(1) + arctan(2) + arctan(3) = ?

Page 1 = arctan(1) + arctan(2) + arctan(3) ?



[PDF] dspArctanpdf - Math et info

Page 1 Somme d'arctangentes arctan(1) + arctan(2) + arctan (3) = ?



[PDF] CM4-transpdf - Cours de Mathématiques L1 Semestre 1

cos : R ? [-11] n'est pas une bijection Mais cos : [0?] ? [-11] est continue et strictement décroissante Sur arctan(tan(x)) = x Vx ? ]-?



[PDF] La fonction Arctangente

La fonction Arctangente I Rappels sur la fonction tangente 1°) Définition sin tan cos x x x = tan x existe pour tout réel x qui n'est pas de la forme



[PDF] 1 Convergence et somme des séries : ? arctan 1 n2 + 3n + 3 ? 3n

sn est une somme partielle télescopique : sn = vn ? v?1 = arctan n + 2 ? arctan 1 (sn) a une limite S = ?/4 donc ? un est convergente de somme S





[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés

On note arccos : [?11] ? [0?] la fonction réciproque i e si ?1 ? x ? 1 alors y = arccosx ? cosy = x ET 0 ? x ? ? 1 3 arctan



[PDF] La fonction Arctangente

La courbe de la fonction « tangente » ressemble à un électrocardiogramme On vérifie le tracé sur la calculatrice graphique Page 2 II Généralités 1 



[PDF] [PDF] Exo7 - Exercices de mathématiques

Calculer arccosx+arcsinx pour x élément de [?11] 2 Calculer arctanx+arctan 1 x pour x réel non nul 3 Calculer cos(arctana) et sin(arctana) pour a réel 





[PDF] 254 Compléments (fonctions trigonométriques inverses)

arctan est dérivable sur R et on a arctan(x)' = 1 1 + x2 IV Complément à la liste des primitives des fonctions usuelles: ? désignant une constante réelle 



[PDF] I Propriétés fondamentales - Normale Sup

Le graphe de f?1 est le symétrique du graphe de f par rapport à la droite y = x III 2 Les fonctions arccos arcsin arctan (a) La fonction x ?? cosx induit 



[PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques

Trouvons une fonction réciproque de cos D'abord cos : R ? [-11] n'est pas une bijection Mais cos : [0?] ? [-11] est continue et strictement 



[PDF] Formulaire de trigonométrie 1 Fonctions trigonométriques - LPSM

] Ces trois fonctions vérifient les formules suivantes : arccos(x) + arcsin(x) = ? 2 arctan 



[PDF] Université de Provence

1 tan ( arctan(b) ) = cotan( arctan(b)) = tan (? 2 ? arctan(b)) Or a Soit la fonction f définie par f(x) = arctan ?1?sin x 1+sin x

  • Comment calculer arctan de 1 ?

    La valeur exacte de arctan(?1) est ??4 .

  • Quelle est la valeur exacte d'Arctan 1 ?

    Quelle est la valeur d'Arctan 1 ? La valeur de arctan 1 ou tan inverse 1 est égale à ?/4 radians ou 45 degrés .

  • Quel est la valeur de arctan ?

    La règle de la fonction arc tangente de base est f(x)=arctan(x). f ( x ) = arctan ? On note aussi cette fonction f(x)=tan?1(x). f ( x ) = tan ? 1 ?
  • La fonction arcsin est impaire. Elle est dérivable sur ]?1,1[ et sa dérivée est donnée par, pour tout x?]?1,1[, x ? ] ? 1 , 1 [ , (arcsin)?(x)=1?1?x2. ( arcsin ) ? ( x ) = 1 1 ? x 2 . Il faut faire attention au fait que la fonction arcsin est la réciproque de la restriction de sin à l'intervalle [??/2,?/2].
cours du mercredi 1/3/17

Chapitre V Fonctionsarcsin;arccos;arctan

1 Définitions

1.1arcsin

Proposition 1.1La fonctionsin : [=2;=2]![1;1]est une bijection. On notearcsin : [1;1]![=2;=2]la fonction réciproquei.e.si1 x1, alorsy= arcsinx,siny=xET=2x=2. Par exemple, arcsin(p3 2 )6= 2=3mais==3.

Démonstration de la proposition :

8=2x=2;sin0x= cosx0,

>0si=2< x < =2. Doncsinest strictement croissante sur[=2;=2]. En particulier, la fonctionsin : [=2;=2]![1;1]est injective. Surjecti- vité : commesin(=2) =1et commesin=2 = 1, d"après le théorème des valeurs intermédiaires, pour tout1y1, il existe=2x=2tel quesinx=y.q.e.d.1.2arccos Proposition 1.2La fonctioncos : [0;]![1;1]est une bijection. On notearccos : [1;1]![0;]la fonction réciproquei.e.si1x1, alorsy= arccosx,cosy=xET0x.

1.3arctan

Proposition 1.3La fonctiontan : [=2;=2]!Rest une bijection. On notearctan :R![=2;=2]la fonction réciproquei.e.six2R, alorsy= arctanx,tany=xET=2< x < =2.

2 Propriétés

Proposition 2.1a)L esfonctions arctanetarcsinsont impaires maisarccos n"est pas paire; 1 b)les fonctions arctanetarcsinsont strictement croissantes et la fonction arccosstrictement décroissante. c) les fonctions arcsinetarccossont continues sur[1;1], la fonctionarctan est continue surR. d)arcsinest dérivable sur]1;1[et81< x <1;arcsin0x=1p1x2,arccos est dérivable sur]1;1[et81< x <1;arccos0x=1p1x2,arctan est dérivable surRet8x2R;arctan0x=11+x2; e)arcsin(0) = 0,arcsin(1=2) ==6,arcsin(1=p2) ==4,arcsin(p3=2) = =3,arcsin(1) ==2;arccos(0) ==2,arccos(1=2) ==3,arccos(1=p2) = =4,arccos(p3=2) ==6,arccos(1) = 0,arctan(0) = 0,arctan(1) = =4,arctan(1) ==4,arctan(p3) ==3,limx!1arctan(x) ==2;

3 Quelques formules concernantarctan

Proposition 3.1a)arctan1 + arctan2 + arctan3 =;

b)arctan(1=2) + arctan1=5 + arctan1=8 ==4; c)4arctan(1=5)arctan(1=239) ==4; d)2arctan(1=3) + arctan(1=7) ==4; e)limn!1Pnk=0(1)k2k+1==4. Démonstration :a,b,c,d) : on utilise quetan(x+y) =tanx+tany1tanxtanyet donc que :tan(x+y+z) =tanx+tany+tanztanxtanytanz1tanxtanytanytanztanxtanz. Par exemple pour a) : tan(arctan1 + arctan2 + arctan3) =

1+2+31:2:311:22:31:3= 0. Doncarctan1 +

arctan2 + arctan3 =k,k2Z. Or, la fonctionarctanest strictement croissante majorée par=2donc :02n+1arctan1 ==4u2n: q.e.d.2

Chapitre VI Intégration

1 Intégrales des fonctions en escaliers

Soientab2R.

Définition 1On dit qu"une fonctionf: [a;b]!Rest en escaliers s"il existe =fa=t0< ::: < tn=bgune subdivision de l"intervalle telle que pour tout0in1,fest constante (égale à une certaine constanteci2R) sur l"intervalle ouvert]ti;ti+1[. Dans ce cas, on dit que la subdivisionest adaptée àf. Exemple :soitI[a;b]un intervalle. On poseI: [a;b]!Rla fonction telle que

I(x) =8

:1six2I,

0six62I.

La fonctionIest en escaliers.

Exercice 1L"ensembleE([a;b])des fonctions en escaliers sur[a;b]est un sous-Respace vectoriel deR[a;b]l"espace des fonctions :[a;b]!R. Les fonctionsI,Iintervalle ouvert deR, forment une famille génératrice de l"espaceE([a;b].

Remarques :

a) on a f([a;b]) =fci: 0in1g[ff(ti) : 0ing; en particulier fne prend qu"un nombre fini de valeurs et est bornée; b) si 0sont des subdivisions de[a;b](on dit que0est une subdivision plus fine que), alors siest adaptée àf, fonction en escaliers,0aussi. Définition 2Soitfune fonction en escaliers sur[a;b]. Le nombre : n1X i=0(ti+1ti)ci où =fa=t0< ::: < tn=bgest une subdivision adaptée àfetf]ti;ti+1[= c i, est indépendant de la subdivision adaptée àfchoisie. On le note : Z b af : 3 Démonstration de l"indépendance vis à vis de la subdivision : Siest une subdivision adaptée àf, notonsI=Pn1i=0(ti+1ti)cila somme correspondante. Siet0sont des subdivisions adaptées,00= [0est une subdivision adaptée àfet plus fine queet0. Il suffit donc de montrer queI=I00=I0. Posons00=fx0;:::;xmgpour certains a=x0< ::: < xm=bdans[a;b]. Alors =fxi0;:::;xingpour certains indices0 =i0< ::: < in=m. On a alors en notantcjla valeur constante de fsur]xij;xij+1[: I =X j(xij+1xij)cj X ji j+11X i=ij(xi+1xi)cj X i(xi+1xi)c00i=I00

(oùc00iest la valeur constante defsur]xi;xi+1[). De même,I0=I00.q.e.d.Exercice 2SoitIun intervalle contenue dans[a;b]. On aRb

aI=l(I)la longueur de l"intervalleI. 4quotesdbs_dbs45.pdfusesText_45
[PDF] limite arctan infini

[PDF] equivalent de arctan en l'infini

[PDF] tangente hyperbolique dérivée

[PDF] tableau de conjugaison ce2

[PDF] lettre de motivation sorbonne licence

[PDF] fonction hyperbolique exo7

[PDF] dérivée cosh

[PDF] lettre de motivation stage immobilier débutant

[PDF] les fonctions hyperboliques et leurs réciproques pdf

[PDF] trigo hyperbolique

[PDF] lettre de motivation agence immobilière sans experience

[PDF] up and down tome 4

[PDF] ch(2x)

[PDF] up and down saison 4 pdf

[PDF] up and down saison 2 pdf ekladata