[PDF] Feuille dexercices n°10 : Couples de v.a.r. discrètes

View - Download Feuille dexercices n°10 : Couples de v.a.r. discrètes

Previous PDF

Next PDF

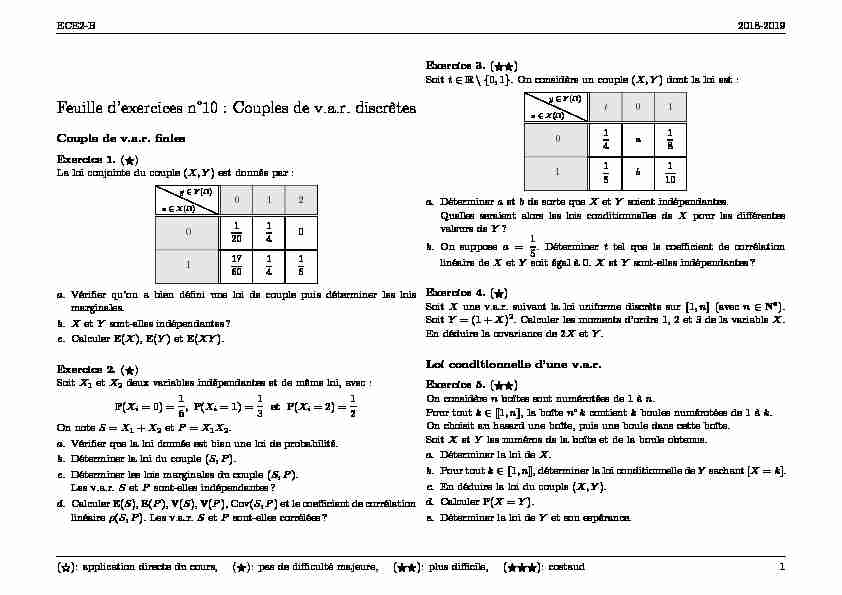
ECE2-B2018-2019Feuille d"exercices n°10 : Couples de v.a.r. discrètes

Couple de v.a.r. finies

Exercice 1.(☀)

La loi conjointe du couple(X;Y)est donnée par :x2X( )y2Y( )012 0 120
14 01 1760
14 16 a.Vérifier qu"on a bien défini une loi de couple puis déterminer les lois marginales. b.XetYsont-elles indépendantes? c.CalculerE(X),E(Y)etE(XY).

Exercice 2.(☀)

SoitX1etX2deux variables indépendantes et de même loi, avec :

P(Xi= 0) =16

;P(Xi= 1) =13 etP(Xi= 2) =12

On noteS=X1+X2etP=X1X2.

a.Vérifier que la loi donnée est bien une loi de probabilité. b.Déterminer la loi du couple(S;P). c.Déterminer les lois marginales du couple(S;P).

Les v.a.r.SetPsont-elles indépendantes?

d.CalculerE(S),E(P),V(S),V(P),Cov(S;P)et le coefficient de corrélation linéaire(S;P). Les v.a.r.SetPsont-elles corrélées?Exercice 3.(☀☀) Soitt2Rn f0;1g. On considère un couple(X;Y)dont la loi est :x2X( )y2Y( )t01 0 14 a18 1 15 b110 a.Détermineraetbde sorte queXetYsoient indépendantes. Quelles seraient alors les lois conditionnelles deXpour les différentes valeurs deY? b.On supposea=15 . Déterminerttel que le coefficient de corrélation linéaire deXetYsoit égal à0.XetYsont-elles indépendantes?

Exercice 4.(☀)

SoitXune v.a.r. suivant la loi uniforme discrète surJ1;nK(avecn2N). SoitY= (1 +X)2. Calculer les moments d"ordre1,2et3de la variableX.

En déduire la covariance de2XetY.

Loi conditionnelle d"une v.a.r.

Exercice 5.(☀☀)

On considèrenboîtes sont numérotées de 1 àn. Pour toutk2J1;nK, la boîtenokcontientkboules numérotées de 1 àk. On choisit au hasard une boîte, puis une boule dans cette boîte. SoitXetYles numéros de la boîte et de la boule obtenus. a.Déterminer la loi deX. b.Pour toutk2J1;nK, déterminer la loi conditionnelle deYsachant[X=k]. c.En déduire la loi du couple(X;Y). d.CalculerP(X=Y).

e.Déterminer la loi deYet son espérance.(?): application directe du cours, (☀): pas de difficulté majeure, (☀☀): plus difficile, (☀☀☀): costaud 1

ECE2-B2018-2019Exercice 6.(☀☀)(d"aprèsESC 2004) Ndésigne un entier naturel supérieur ou égal à 2. Un joueur lance une pièce équilibrée indéfiniment. On noteXNla v.a.r. réelle discrète égale au nombre de fois où, au cours desNpremiers lancers, deux résultats successifs ont été différents. On peut appelerXNle " nombre de changements » au cours deNpremiers lancers. Par exemple, si lesN= 9premiers lancers ont donné successivement : Pile, Pile, Face, Pile, Face, Face, Face, Pile, Pile, alors la variableX9aura pris la valeur4(quatre changements aux3ieme,4ieme,5iemeet8iemelancers).

1.Justifier queXN(

) =J0;N1K.

2.Déterminer la loi deX2, ainsi que son espérance.

Déterminer la loi deX3.

3.Montrer queP(XN= 0) =12

N1 etP(XN= 1) = 2(N1)12 N 4. a) Justifier que :8k2J0;N1K,P[XN=k]([XN+1=k]) =12 b)En déduire que pour toutk2J0;N1K:

P((XN+1XN= 0)\(XN=k)) =12

P(XN=k)

c)En sommant cette relation pourkvariant de0àN1, montrer que

P(XN+1XN= 0) =12

d)Montrer queXN+1XNsuit une loi de Bernoulli de paramètre12

En déduire la relationE(XN+1) =12

+E(XN).

Enfin, donnerE(XN)en fonction deN.

5. a) Montrer grâce aux résultats4.b)et4.c)que les variablesXN+1XN etXNsont indépendantes. b)En déduire par récurrence surNqueXN,! BN1;12

En déduire la varianceV(XN).

6.Écrire un programmeScilabqui simule cette expérience et qui affiche

la valeur d"une réalisation deXN, l"entierNétant entré au clavier par l"utilisateur.Exercice 7.(☀☀)

On considère une expérience aléatoire modélisée par le programme suivant.1functionX= exo(n)

2X= 0

3fori = 1: n

4ifX= 0then

5X= -1 + grand(1,1,"uin",0,1)?2

6else

7X= -1 + grand(1,1,"uin",0,2)

8end 9end

10endfunction

a.Décrire l"expérience ainsi modélisée. b.Pour tout entierk6n, on noteXkla v.a.r. égale aukèmenombre calculé.

DéterminerXk(

)puis la loi deXk+1conditionnée par celle deXk. c.En déduire la loi, l"espérance et la variance deXk. Pouvait-on prévoir la valeur de l"espérance? d.Modifier le programme précédent pour qu"il donne la première valeur (non nulle) dekpour laquelleXk= 0. On noteYcette valeur. e.Donner la loi, l"espérance et la variance deY.

Exercice 8.(☀☀)

Un boulanger possède un ensemble de pochettes surprise. Lorsqu"on en achète une, on peut : soit gagner une montre avec une probabilitém, soit gagner un euro avec la probabilitée, soit ne rien gagner. Un client achètenpochettes surprise, avecn2N. On désigne parMla v.a.r. égale au nombre de montres gagnées etEla v.a.r. égale au nombre

d"euros gagnés.(?): application directe du cours, (☀): pas de difficulté majeure, (☀☀): plus difficile, (☀☀☀): costaud 2

ECE2-B2018-20191.Soitn2N. Soitx2R. CalculernP

k=0kn k x ken fonction denet dex. 2. a) Déterminer la loi deM. b)Déterminer la loi conjointe du couple(M;E).

3.On suppose quekpochettes ont rapporté quelque chose.

SoitTkla v.a.r. égale à la proportion de montres par rapport au nombre de pochettes ayant rapporté quelque chose.

Déterminer la loi deTk.

Calculer l"espérance deTken fonction demet dee.

Loi d"une somme de v.a.r. discrètes

Exercice 9.(☀☀)

On lance un dé indéfiniment. On noteXla v.a.r. égale au nombre de lancers nécessaires pour obtenir le premier6. On noteYla v.a.r. nombre de lancers nécessaires, après l"obtention du pre- mier6, pour obtenir le deuxième6. a.Déterminer les lois deX, deY, leurs espérance et leurs variances. b.SoitZ=X+Y. Déterminer l"espérance et la variance deZ. c.Déterminer la loi deZ. d.Interpréter ce que représenteZ. Retrouver directement la loi deZ.

Exercice 10.(☀☀)

Soit(Xn)n2Nune suite de v.a.r. mutuellement indépendantes. On admet que, pour toutn>2,X1+:::+XnetXn+1sont indépendantes. On suppose queXi,! P(1)et, pour toutn2N, on considère : S n=nP k=1X ketSn=Snnpn a.Montrer queSnsuit une loi de Poisson de paramètren. b.En déduireE(Sn)etV(Sn). c.Déterminer l"espérance et la variance deSn. d.Montrer que pour toutn2N,P([Sn60]) =ennP k=0n kk!.Exercice 11.(☀☀) SoientXetYdeux variables aléatoires discrètes indépendantes.

NotonsZla v.a.r. définie parZ=X+Y.

1)On suppose queX ,! P()etY ,! P().

a.Démontrer que :

8k2N;[X+Y=k] =kS

`=0[X=`]\[Y=k`] b.Déterminer la loi deZ.

2)On suppose queX ,! G(p)etY ,! G(p).

a.Démontrer que :

8k2Nn f0;1g;[X+Y=k] =k1S

`=1[X=`]\[Y=k`] b.Déterminer la loi deZ.

Exercice 12.(☀☀)(d"aprèsEDHEC 1999)

SoientX;YetZtrois v.a.r. mutuellement indépendantes et définies sur le même espace probabilisé( ;A;P). On suppose queX;YetZsuivent la loi uniforme discrète surJ1;nK. 1. a) Montrer que :8k2J2;n+ 1K; P(X+Y=k) =k1n 2. b)Montrer que :8k2Jn+ 2;2nK; P(X+Y=k) =2nk+ 1n 2.

2.Utiliser la formule des probabilités totales pour déduire de la première

question que :P(X+Y=Z) =n12n2. 3. a) Montrer que la variable aléatoireT=n+ 1Zsuit la loi uniforme discrète surJ1;nK. b)PourquoiTest-elle indépendante deXet deY? c)En faisant intervenir la variableTet en utilisant la deuxième question,

déterminer la probabilitéP(X+Y+Z=n+ 1):(?): application directe du cours, (☀): pas de difficulté majeure, (☀☀): plus difficile, (☀☀☀): costaud 3

ECE2-B2018-2019Indépendance de v.a.r. discrètes

Exercice 13.(☀☀)

Une urne contientN2boules vertes, 1 boule blanche et 1 boule rouge. On tire les boules de l"urne, une à une et sans remise.

1.SoitX1le rang d"apparition de la boule blanche,X2le rang d"apparition

de la boule rouge. a)Déterminer la loi deX1, la loi deX2, la loi du couple(X1;X2). b)Les variablesX1etX2sont-elles indépendantes?

2.SoitXle rang où on obtient pour la première fois soit la boule blanche,

soit la boule rouge. SoitYle rang où on a obtenu pour la première fois les deux boules blanche et rouge. a)Déterminer la loi deXet la loi deY. b)Calculer les espérances deXet deY.

Exercice 14.(☀☀)

Soit(Xn)n2Nune suite de variables de Bernoulli de paramètrep(0< p <1), indépendantes. Pour toutn2N, on poseYn=XnXn+1etTn=nP i=1Y i. a.Déterminer, pour toutn2N, la loi deYn, son espérance et sa variance. b.Déterminer, pour toutn2N, la loi de(Yn;Yn+1)etCov(Yn;Yn+1). c.Déterminer, pour toutn2Net tout entierk>2, la loi de(Yn;Yn+k).

Les variablesYnetYn+ksont-elles indépendantes?

d.CalculerE(Tn)etV(Tn).

Exercice 15.(☀☀)(d"aprèsEML 2007)

On considère deux v.a.r.UetYdéfinies sur un même espace probabilisé ;A;P). On suppose que les variablesUetYsont indépendantes,Usuit la loi de Bernoulli de paramètre12 et la loi deYest donnée par : Y( ) =Net8n2N;P(Y=n) =11e en. On noteT= (2U1)Y. a.Montrer queY+1suit une loi géométrqiue dont onprécisera le paramètre.

En déduire l"espérance et la variance deY.

b.Montrer queTadmet une espéranceE(T), et calculerE(T).Exercice 16.(☀☀) Deux urnesU1etU2contiennent des boules blanches et des boules noires.

Plus précisément :

U1contient 2 boules blanches et 2 boules noires,

U2contient 1 boule blanche et 3 boules noires.

On effectue une suite de tirages avec remise de la boule tirée en procédant comme suit :

Le premier tirage s"effectue dansU1.

Si aunèmetirage on obtient une boule blanche alors le(n+1)-ième tirage s"effectue dansU1. Si aunèmetirage on obtient une boule noire alors le(n+ 1)-ième tirage s"effectue dansU2.

On désigne par :

pnla probabilité d"obtenir une boule blanche aunèmetirage, Xnla v.a.r. qui vaut 1 si la boule obtenue aunèmetirage est blanche, 0 sinon. Snest le nombre total de boules blanches obtenues au bout dentirages. a.Calculerp1etp2. b.Déterminer une relation entrepn+1etpn. En déduire l"expression depn en fonction den, et la limite depnquandntend vers+1. c.Pournsupérieur ou égal à 1, donner la loi deXn.

PréciserE(Xn)etV(Xn).

d.Les v.a.r.X1etX2sont-elles indépendantes? e.ExprimerSnen fonction desXk;16k6n. En déduireE(Sn).

Exercice 17.(☀☀)

SoitXune v.a.r. de loi uniforme surJ1;1K. On noteY=X2. a.Montrer que les v.a.r.XetYne sont pas indépendantes.

b.CalculerCov(X;Y). Commenter.(?): application directe du cours, (☀): pas de difficulté majeure, (☀☀): plus difficile, (☀☀☀): costaud 4

ECE2-B2018-2019Événement dépendant de deux v.a.r. discrètes

Exercice 18.(☀☀)

On considère un lot de 10 dés cubiques dont les faces sont numérotées de 1 à

6. Sur ces 10 dés, cinq sont équilibrés, les cinq autres sont truqués. Pour un

dé truqué, la probabilité d"obtenir1quand on le lance sera prise égale à56

1.On choisit un dé au hasard, on le lance 3 fois et on obtient 3 fois la face

n o1. Quelle est la probabilité de l"événement : " le dé choisi est truqué »?

2.On effectue des lancers successifs d"un dé équilibré et on arrête dès que

l"on a obtenu pour la première fois la face n o1. SoitXla v.a.r. égale au nombre de lancers effectués avec ce dé. On effectue des lancers successifs d"un dé truqué et on arrête dès que l"on a obtenu pour la première fois la face n o1. SoitYla v.a.r. égale au nombre de lancers effectués avec ce dé. a)Déterminer la loi deXet calculer l"espérance et la variance deX. b)Déterminer la loi deYet calculer l"espérance et la variance deY.

3.Calculer la probabilité de l"événement[X=Y].

4.Calculer la probabilité de l"événement[X < Y].

5.On prend un dé truqué, on effectue des lancers successifs et on arrête dès

que l"on a obtenu pour la première fois une face ne portant pas le n o1. SoitZla v.a.r. égale au nombre de lancers effectués avec ce dé. Déterminer la loi de probabilité de la v.a.r.X+Zet calculer son espérance.

Exercice 19.(☀☀)

Deux personnesAetBpartent en vacances de façon indépendante dans un paysE. Leur séjour dans ce pays peut s"étaler surnjournées (n >3) numérotées1,2, ...,n. Pour éventuellement s"y rencontrer, elles ont projeté d"y séjourner trois jours consécutifs (et trois jours seulement) dans un hôtelH, choisi par elles. On suppose que les jours d"arrivée possibles 1, 2, . . . ,n2de ces deux personnes dans cet hôtel sont deux v.a.r. uniformes et indépendantes.

Les arrivées ont lieu le matin et les départs le soir deux jours plus tard.1.a) Quelle est la probabilité queAetBarrivent le même jour?

b)Quelle est la probabilité qu"elles arrivent avec un jour d"écart? c)Quelle est la probabilité qu"elles puissent se rencontrer dans l"hôtel?

2.Sachant queAetBse sont rencontrées, quelle est la probabilité qu"elles

ne puissent passer qu"une journée ensemble? Exercice 20.(☀☀)(d"aprèsECRICOME 2000) On considère une urne contenant des boules blanches (en proportionp), des boules rouges (en proportionr) et des boules vertes (en proportionu).

On suppose quep>14

,r>14 ,u>14 et quep+r+u= 1. On effectue indéfiniment des tirages successifs d"une boule dans cette urne avec remise entre deux tirages. Pour toutn2N, on noteBn(respectivementRn,Vn) l"événement : " Tirer une boule blanche (respectivement rouge, verte) auniemetirage ». On appelleX(respectivementY) la v.a.r. égale au rang d"apparition de la première blanche (respectivement rouge). On définit alors la variableD=jXYjégale au nombre de tirages séparant la sortie de la première blanche et de la première rouge. 1. a) Déterminer la loi deX. b)Déterminer la loi deY.

2.Soitietjdes entiers naturels non nuls.

a)En distinguant les casi=j,i < jeti > j, exprimer l"événement [X=i]\[Y=j]à l"aide des événements décrits dans l"énoncé. b)En déduire la loi du couple(X;Y).

3.Les variablesXetYsont-elles indépendantes?

4.Soitkun entier naturel non nul, montrer l"égalité :

P([D=k]) =prp+r

(1p)k1+ (1r)k1(?): application directe du cours, (☀): pas de difficulté majeure, (☀☀): plus difficile, (☀☀☀): costaud 5

ECE2-B2018-2019Coefficient de corrélation linéaire

Exercice 21.(☀☀)

SoientXetYdeux v.a.r. discrètes. On noteP() =V(X+Y). 1. a) Démontrer quePest un polynôme du deuxième degré en. b)Prouver quePest toujours positif. c)En déduire le signe de son discriminant. d)En déduire quejCov(X;Y)j6(X)(Y).

2.On suppose que(X;Y) =1.

a)Déterminer le discriminant deP. b)En déduire qu"il existe un réelatel queV(aX+Y) = 0. c)Que peut-on en déduire surXetY?

Exercice 22.(☀☀)(d"aprèsESG 95)

Le nombre de voitures vendues par un concessionnaire chaque jour est une v.a.r.Xqui suit une loi de Poisson de paramètre. Lorsqu"un client se présente pour acheter une voiture, on admet que la pro- babilité qu"il demande un crédit est égale àp, avec0< p <1. SoitYla v.a.r. égale au nombre de clients qui dans la journée demandent un crédit pour acheter une voiture.

1.Pour tout(k;n)2N2, calculerP[X=n]([Y=k]).

2.Déterminer la loi conjointe du couple(X;Y).

3.Déterminer la loi deY, puis calculer l"espérance et la variance deY.

4.SoitZla v.a.r. égale au nombre de clients qui achètent dans la journée

une voiture au comptant. a)Déterminer la loi deZ. b)Les variablesYetZsont-elles indépendantes?

5.En remarquant queY+Z=X, déterminer la covariance deXetY.

6. a) CalculerX;Y, le coefficient de corrélation linéaire deXetY. b)Commenter le signe deX;Y.

Les variablesXetYsont-elles indépendantes?

c)Xpeut-elle être une fonction affine deY?Exercice 23.(☀☀) Démontrer que deux variables de Bernoulli sont indépendantes si, et seule- ment si, elles sont non corrélées.

Exercice 24.(☀)

On considère trois v.a.r.U,V, etW, indépendantes et telles queUetW suivent la loi de Poisson de paramètre >0, etVsuit la loi de Poisson de paramètre >0.

On noteX=U+VetY=V+W.

1.Rappeler les lois deXet deY.

2. a) Montrer queCov(X;Y)existe et la calculer b)En déduire le coefficient de corrélation linéaire deXetY.

Exercice 25.(☀☀☀)

Soientaun entier naturel non nul, etnun entier naturel supérieur ou égal à

2. À un péage d"autoroute comportantnguichets,navoitures se présentent.

Chaque conducteur choisit un guichet au hasard, de manière équiprobable. Les choix des automobilistes sont supposés indépendants entre eux. On note X ile nombre de voitures étant passées par le guichet numéroi. On noteY la v.a.r. égale au nombre de guichets où ne se sont présentée aucune voiture. 1. a) Déterminer la loi, l"espérance et la variance de la v.a.r.Xi. b)CalculerV(X1+X2++Xn). c)En déduire Cov(Xi;Xj)oùietjsont des entiers distincts quelconques deJ1;nK.

2.Calculer le coefficient de corrélation linéaire deXietXjoùietjsont

des entiers distincts quelconques deJ1;nK. Commenter le casn= 2.

3.On noteYila variable de Bernoulli égale à1si aucune voiture n"est passée

au guichet n°i, et égale à0sinon. a)Pour touti2J1;nK, déterminer la loi de la variableYi, son espérance et sa variance. b)Exprimer la variableYen fonction des variablesY1;Y2;:::;Yn.

c)En déduire l"espérance et la variance deY.(?): application directe du cours, (☀): pas de difficulté majeure, (☀☀): plus difficile, (☀☀☀): costaud 6

ECE2-B2018-2019Exercice 26.(☀☀)

Une urne contientNjetons numérotés1;2;:::k, avec26k6N. Pouri2J1;kK, on notenile nombre de jetons portant le numéroietpi=niN

On suppose que0< pi<1, pour touti2J1;kK. Soitn2N.

On effectue dans cette urnentirages successifs d"un jeton avec remise.

1.Pour touti2J1;kK, on noteNila v.a.r. égale au nombre de jetons tirés

portant le numéroi. Déterminer la loi deNi, son espérance et sa variance. 2. a) Pour(i;j)2J1;kK2tel quei6=j, déterminer la loi deNi+Nj, son espérance et sa variance. b)Soit(i;j)2J1;kK2tel quei6=j. CalculerCov(Ni;Nj)et vérifier que le coefficient de corrélation de(Ni;Nj)est bien entre1et1. Dans quel cas vaut-il1? Que pensez-vous de ce résultat? 3. a) On poseZnla variable prenant pour valeur le nombre de numéros qui ne sont pas sortis. Calculer, sans passer par sa loi, l"espéranceE(Zn) deZnet calculerlimn!+1E(Zn). b)ComparerP(Zn>1)etE(Zn)et montrer quelimn!+1P(Zn= 0) = 1:

Loi d"unmin, d"unmax

Exercice 27.(☀☀)

On considère une urne contenantnboules numérotées de1ànet on tire au hasard deux boules, avec remise dans cette urne. On noteXla v.a.r. égale au numéro de la première boule etYla v.a.r. au numéro de la deuxième boule. a.Justifier queXetYsont indépendantes. b.On poseS= max(X;Y). DéterminerP(S6k)puis donner la loi deS. c.On poseT= min(X;Y). DéterminerP(T > k)puis donner la loi deT

Exercice 28.(☀☀)

On considèreBetGdeux v.a.r. indépendantes suivant respectivement une loi de BernoulliB(p)et une loi géométriqueG(p0). a.Déterminer la loi de la v.a.r.BG. b.CalculerE(BG).Exercice 29.(☀☀) SoientXetYdeux variables aléatoires discrètes indépendantes. On suppose queX ,! G(p1)etX ,! G(p2)oùp1etp2sont dans]0;1[.

NotonsZ= min(X+Y)etT= max(X;Y). Soitn2N.

1. a) DéterminerP([X > n]). b)Déterminer alorsP([Z > n]). c)Comment peut-on exprimer[Z=n]en fonction d"événements de la famille([Z > k])k2N? d)En déduireP([Z=n])et reconnaître alors la loi suivie parZ. 2. a) DéterminerP([T6n])puisP([T > n]). b)Démontrer que :P([T=n]) =P([T > n1])P([T > n]). c)Soitm2N.

Démontrer que :

mP n=1nP([T=n]) =m1P n=0P([T > n])mP(T > m). d)Démontrer queTadmet une espérance et la calculer.

Exercice 30.(☀☀)

Trois personnesa1;a2;a3entrent à l"instant 0 dans un bureau de poste qui ne comporte que deux guichets. Les personnesa1eta2peuvent être servies immédiatement alors quea3doit attendre qu"un guichet soit libéré pour être servie. On supposera que le temps est mesuré par des nombres entiers avec une unité fixée. Soitp2]0;1[. On suppose que pouri2 f1;2;3gle temps de service de la personneaiest une v.a.r.Xidont la loi est donnée par : pour toutk2quotesdbs_dbs32.pdfusesText_38

[PDF] exercice probabilité couple variable aléatoire

[PDF] couple de variables aléatoires discrètes

[PDF] variable aléatoire exercices corrigés pdf

[PDF] couples de variables aléatoires réelles exercices corrigés

[PDF] couple de variables aléatoires continues

[PDF] couple difference age 20 ans

[PDF] mariage femme plus agée que l homme bible

[PDF] différence age couple statistiques

[PDF] couple redox co2/c

[PDF] communication dans le couple psychologie pdf

[PDF] psychologie couple communication

[PDF] tableau couple oxydant réducteur

[PDF] classification des couples redox pdf

[PDF] couple redox no3- no

[PDF] couple redox so42-/so2