Cours limites PDF Limites. LIMITES DE FONCTIONS. I.

LIMITES ET CONTINUITÉ (Partie 1)

- Il existe des fonctions qui ne possèdent pas de limite infinie. C'est le cas des fonctions sinusoïdales. 3) Limites des fonctions usuelles. Propriétés : - lim.

Limites – Corrections des Exercices

(limite de quotient de fonctions). — b. g(x)=5x − 1 +. 1 x − 3 en +∞

Limites de fonctions cours

http://mathsfg.net.free.fr/premiere/1S2010/limitesfonctions/limitescours1S.pdf

LIMITES DES FONCTIONS

( ) = la droite d'équation = est appelée asymptote horizontale à la courbe de la fonction en +∞. Page 3. Yvan Monka – Académie de Strasbourg –

de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n˚1

3. Déterminer les limites en 1 et la limite en +∞. Que peut-on en déduire pour (Cf )?. 4. Calculer la fonction dérivée de f et étudier son signe. 5. Dresser

Limites de fonctions - Lycée dAdultes

9 oct. 2014 limite à droite. Limite à gauche. PAUL MILAN. 3. TERMINALE S. Page 4. TABLE DES MATIÈRES. 3 Limites des fonctions élémentaires. Limites en l' ...

FONCTION EXPONENTIELLE

Comme. la fonction exponentielle est strictement croissante. 3) Limites en l'infini première lettre du mot exponentiel. expx exp −x. ( )= exp x − x.

Leçon 1 : LIMITES Cours LIMITES ET CONTINUITÉ

Un trait (ou une ligne) est dit continue s'il ne présente aucun saut. Autrement dit on peut le tracer sans lever le crayon. Oup's ! Soit f une fonction définie

fondmath1.pdf

Apprendre ses cours et s'entraîner : en mathématiques le talent a ses limites comme

[PDF] Analyse - Exo7 - Cours de mathématiques

s alors elle parcoure la première moitié en. 1 s

Limites de fonctions cours

http://mathsfg.net.free.fr/premiere/1S2010/limitesfonctions/limitescours1S.pdf

LIMITES ET CONTINUITÉ (Partie 1)

On dit que la fonction f admet pour limite L en +? si tout intervalle ouvert contenant 6. 3) Limite d'un quotient lim x?? f (x) =.

livre-analyse-1.pdf - Exo7 - Cours de mathématiques

dans lesquels le formalisme mathématique s'applique et permet de résoudre des problèmes. fonctions : limite continuité

Cours danalyse 1 Licence 1er semestre

Exercice 3.1. Calculer les limites des suites données par les termes généraux suivants : n3. ?3 + sinn. cos(.

Limites asymptotes EXOS CORRIGES

Cours et exercices de mathématiques 6 x x x ? ?. ?. ?. ?. Exercice n°19. Retrouver les limites de f(x) à partir du graphique ... 1ère manière :.

Cours limites

Limites. LIMITES DE FONCTIONS. I. LIMITE en + ? et en – ? grandes vers + ? les nombres f (x) viennent s'accumuler autour de L . On note : lim.

de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n?1

Déterminer les limites en 1 et la limite en +?. Que peut-on en déduire pour (Cf )?. 4. Calculer la fonction dérivée de f et étudier son signe. 5. Dresser

Chapitre 3 Dérivabilité des fonctions réelles

Cette limite s'appelle la dérivée de f en x0 on la note f (x0). Bien sûr

COURS DE MATHÉMATIQUES PREMI`ERE ANNÉE (L1

19 Courbes paramétrées et développements limités page 167 langue française et on consid`ere l'ensemble S des nombres entiers que l'on peut définir `a.

[PDF] LIMITES ET CONTINUITÉ (Partie 1) - maths et tiques

Yvan Monka – Académie de Strasbourg – www maths-et-tiques 1 LIMITES ET CONTINUITÉ (Partie 1) I Limite d'une fonction à l'infini 1) Limite finie à

[PDF] Cours limites

Les courbes représentant ces fonctions admettent l'axe des ordonnées comme asymptote verticale b Limite finie en a Exemples : limx ? 3 sin (3 x + 4) = sin

[PDF] Leçon 1 : LIMITES Cours LIMITES ET CONTINUITÉ - cloudfrontnet

Limites et Continuité _ Tles S (C D E F) Page 1 / 12 Powered by www educamer Etudier les limites en a en distinguant éventuellement deux cas :

[PDF] Limites de fonctions

Si f est une fonction définie sur un intervalle f a pour limite le réel quand x tend vers l'infini si les images f(x) sont aussi proches que l'on veut de à

Limites et asymptotes : cours de maths en 1ère en PDF - Mathovore

Les limites de fonctions et l'étude des asymptotes horizontale verticales obliques dans un cours de maths en 1ère où nous aborderons la définition de

[PDF] Limites de fonctions cours première S Table des matières - Mathsfg

10 jui 2009 · Limites de fonctions cours classe de première S 1 Limites finies à l'infini Soit f une fonction définie sur un intervalle [a;+?[ où a

[PDF] Limites de fonctions - Lycée dAdultes

9 oct 2014 · 2 Limite infinie en un point 3 3 Limites des fonctions élémentaires 4 4 Opérations sur les limites 4 4 1 Sommedefonctions

[PDF] Limites et continuité

Limites et continuité UJF Grenoble 1 Cours 1 1 Vocabulaire au voisinage de x s'il existe un intervalle ouvert I contenant x tel que la restric-

[PDF] Limites et continuité - Fontaine Maths

Cours de mathématiques ECT1 1 5 Limite finie en l'infini Lorsqu'une fonction f est définie au voisinage de +? ou de ?? on peut s'intéresser au

[PDF] Limite dune fonction numerique - AlloSchool

tion y = l est asymptote (horizontale) à la courbe représentant f Chapitre 9 Limite d'une fonction numerique Cours de 1ere S Sciences Expirémentales

LIMITES DE FONCTIONS

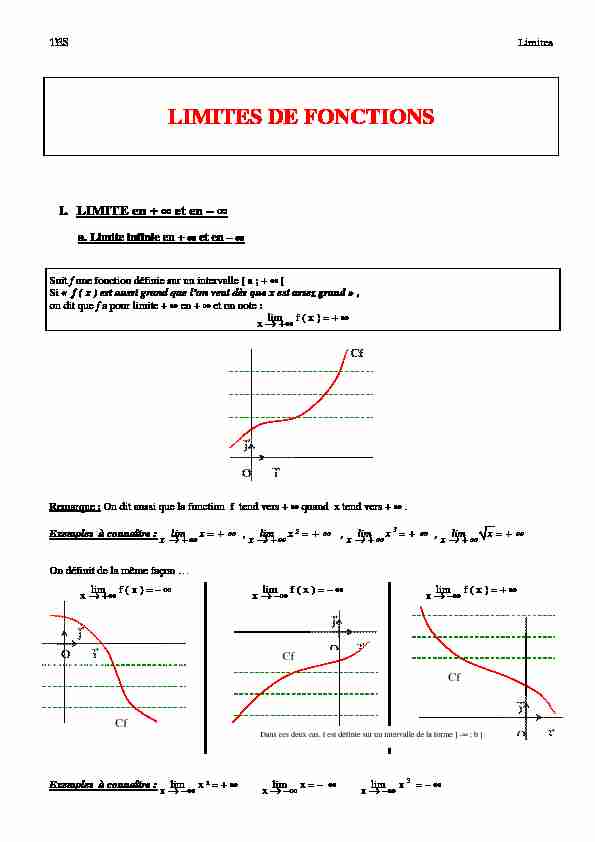
I. LIMITE en + ¥¥¥¥ et en - ¥¥¥¥ a. Limite infinie en + ¥¥¥¥ et en - ¥¥¥¥ Soit f une fonction définie sur un intervalle [ a ; + ¥ [ Si " f ( x ) est aussi grand que l"on veut dès que x est assez grand » , on dit que f a pour limite + ¥ en + ¥ et on note : limx ® +¥ f ( x ) = + ¥ Remarque : On dit aussi que la fonction f tend vers + ¥ quand x tend vers + ¥ .

Exemples à connaître :

limx ® +¥ x = + ¥ , limx ® +¥ x ² = + ¥ , limx ® +¥ x 3 = + ¥ , limx ® +¥ x = + ¥

On définit de la même façon ...

limx ® +¥ f ( x ) = - ¥ limx ® -¥ f ( x ) = - ¥ limx ® -¥ f ( x ) = + ¥

Exemples à connaître : limx ® -¥ x ² = + ¥ limx ® -¥ x = - ¥ limx ® -¥ x 3 = - ¥

¾®j

¾®i

¾®j

¾®i

¾®j

¾®i

¾®j

¾®i

Cf Cf Dans ces deux cas, f est définie sur un intervalle de la forme ] -¥ ; b ] b. Limite finie en + ¥¥¥¥ et en - ¥¥¥¥ et asymptote horizontale Soit f une fonction définie sur un intervalle I

Intuitivement, dire que f a pour limite L en + ¥ , signifie que lorsque x prend des valeurs de plus en plus

grandes vers + ¥ , les nombres f (x) viennent s"accumuler autour de L .

On note :limx ® +¥ f ( x ) = L

On dit que la droite d"équation y = L est asymptote horizontale

à la courbe Cf en + ¥ .

Remarques :

· On obtient la même chose en remplaçant + en - · Une fonction n"a pas forcément une limite finie ou infinie quand x tend vers + ¥ . ( Par exemple x ½¾¾® sin x , x ½¾¾® cos x ... )

Exemples à connaître :

limx ® +¥ 1 x = 0 , limx ® +¥ 1 x² = 0 , limx ® +¥ 1 x3 = 0 , limx ® +¥ 1 x = 0 limx ® -¥ 1 x = 0 , limx ® -¥ 1 x² = 0 , limx ® -¥ 1 x3 = 0 c. Asymptote oblique Soit C la courbe représentant une fonction f dans un repère.

Dire que la droite d"équation y = a x + b est asymptote oblique à C en + ¥ revient à dire que :

limx ® +¥ [] f (x) - (ax + b) = 0 Remarque : On obtient la même chose en remplaçant + en - f ( x ) x y N M C L f ( x )

¾®j

¾®i x

II. LIMITE en a

a. Limite infinie en a et asymptote verticale

Soit f une fonction

Si " f ( x) est aussi grand que l"on veut dès que x est assez proche de a » , on dit que f a pour limite + ¥

en a et on note : limx ® a f ( x ) = + ¥ On définit de la même façon limx ® a f ( x ) = - ¥ On dit que la droite d"équation x = a est asymptote verticale à la courbe Cf

Remarque :

Il arrive souvent qu"on soit amené à définir des limites " d"un seul côté de a » . Naturellement, on introduit les notions de limite à droite en a et de limite à gauche en a et on note :

limx ® a+ f ( x ) et limx ® a- f ( x ) ou encore limx ® a f ( x ) et limx ® a f ( x )

x > a x < a

Exemples à connaître :

limx ® 0+ 1 x = + ¥ , limx ® 0+ 1 x² = + ¥ , limx ® 0+ 1 x3 = + ¥ , limx ® 0+ 1 x = + ¥ limx ® 0- 1 x = - ¥ , limx ® 0- 1 x² = + ¥ , limx ® 0- 1 x3 = - ¥

Les courbes représentant ces fonctions admettent l"axe des ordonnées comme asymptote verticale .

Limite finie en a

Exemples : limx ® 3 sin (3x + 4) = sin 13 , limx ® 4 x² + 3 = 19

O x

y Cf Dans ce cas lim x ® a+ f ( x ) = - ¥ et lim x ® a- f ( x ) = + ¥ a

O a

III. OPERATION SUR LES LIMITES

Les théorèmes qui suivent, présentés sous forme de tableau sont admis.

Pour la plupart d"entre eux , ils sont naturels mais ... comme souvent en math, il y a quelques cas particuliers.

Par convention et pour simplifier :

On note lim f et lim g les limites de f et de g , toutes les deux en a , en + ¥ ou en - ¥

On note par un point d"interrogation les cas où il n"y a pas de conclusion générale. On dit qu"il s"agit de cas

de formes indéterminées . Ces cas nécessiteront une étude particulière chaque fois qu"ils se présenteront.

a. Limite de k f lim f L + ¥ - ¥ lim k f ( avec k > 0 ) k L + ¥ - ¥ lim k f ( avec k < 0 ) k L - ¥ + ¥ Exemple : Soit la fonction g définie sur IR* par g : x ½¾¾® - 2 x²

limx ® -¥ g ( x ) = 0 , limx ® +¥ g ( x ) = 0 , limx ® 0+ g ( x ) = - ¥ et limx ® 0- g ( x ) = - ¥

b. Limite de f + g lim f L L L + ¥ - ¥ + ¥ lim g L" + ¥ - ¥ + ¥ - ¥ - ¥ lim ( f + g ) L + L" + ¥ - ¥ + ¥ - ¥ ? Exemple : Soit la fonction h définie sur IR+* par h : x ½¾¾® x - 2 x² .

On a h = f + g avec f : x

½¾¾® x et g : x ½¾¾® - 2 x²

On sait que limx ® +¥ f ( x ) = + ¥ et limx ® +¥ g ( x ) = 0 ; donc limx ® +¥ h ( x ) = + ¥

c. Limite de f. g lim f L L > 0 L > 0 L < 0 L < 0 + ¥ + ¥ - ¥ 0 lim g L" + ¥ - ¥ + ¥ - ¥ + ¥ - ¥ - ¥ +/- ¥ lim ( f .g ) L ´ L" + ¥ - ¥ - ¥ + ¥ + ¥ - ¥ + ¥ ? Exemple : Soit la fonction h définie sur IR+ par h : x ½¾¾® ( x + 2 ) x

On a h = f ´ g avec f : x

½¾¾® x + 2 et g : x ½¾¾® x On sait que limx ® 0 f ( x ) = 2 et limx ® 0 x = 0 ; donc limx ® 0 h ( x ) = 0 d. Limite de f/g Cas où la limite de g n"est pas nulle Cas où la limite de g est nulle lim f L L + ¥ + ¥ - ¥ - ¥ +/- ¥ L > 0 ou + ¥ L > 0 ou + ¥ L < 0 ou - ¥ L < 0 ou - ¥ 0 lim g L" +/- ¥ L" > 0 L" < 0 L" > 0 L" < 0 +/- ¥ 0 + 0 - 0 + 0 - 0

lim f/g L/L" 0 + ¥ - ¥ - ¥ + ¥ ? + ¥ - ¥ - ¥ + ¥ ?

Exemple : Soit la fonction h définie sur IR+* par h : x ½¾¾® 2x - 4x

On a h = f

g ou f : x ½¾¾® 2 x - 4 et g : x ½¾¾® x

On sait que limx ® 0+ f ( x ) = - 4 et limx ® 0+ g ( x ) = 0+ ; d"où limx ® 0+ h ( x ) = - ¥

quotesdbs_dbs33.pdfusesText_39

[PDF] correspondance commerciale gratuite

[PDF] comment transformer le courant alternatif en continu pdf

[PDF] comment transformer le courant continu en alternatif

[PDF] passer du courant continu au courant alternatif

[PDF] la monnaie cours pdf

[PDF] la création monétaire cours s3

[PDF] création monétaire dissertation

[PDF] cours cristallographie mpsi

[PDF] cours cristallochimie:pdf

[PDF] les différentes formes de cybercriminalité pdf

[PDF] cycle de l'eau explication

[PDF] résumé cycle de l'eau

[PDF] les différentes étapes du cycle de l'eau

[PDF] cycle de l'eau schéma simple

[PDF] cycle de l'eau schéma ? compléter

[PDF] Cours limites Limites. LIMITES DE FONCTIONS. I.

LIMITES DE FONCTIONS

Exemples à connaître :

On définit de la même façon ...

¾®j

¾®i

¾®j

¾®i

¾®j

¾®i

¾®j

¾®i

On note :limx ® +¥ f ( x ) = L

à la courbe Cf en + ¥ .

Remarques :

Exemples à connaître :

¾®j

¾®i x

II. LIMITE en a

Soit f une fonction

Remarque :

Exemples à connaître :

Limite finie en a

O x

O a

III. OPERATION SUR LES LIMITES

Par convention et pour simplifier :

On a h = f + g avec f : x

On a h = f ´ g avec f : x

On a h = f