Exercices avec corrigé succinct du chapitre 5 PDF

2 10. Exercice 6. Splines cubiques. Dans cet exercice nous souhaitons interpoler une fonction f 2 C 2([a

Option B : Examen du 5 Janvier Splines cubiques 1 A propos de l

On souhaite calculer en Scilab la spline cubique interpolante π correspondant à ces données et évaluer numérique- ment l'erreur d'interpolation entre f et π (

Réponses aux exercices du chapitre 5

Le polynôme d'interpolation par Lagrange est donné par : pn(x) = n a) Obtenir le système linéaire de dimension 3 permettant de calculer la spline cubique.

TD1 : Interpolation et splines

Exercice 3 (Interpolation d'Hermite). On se donne n + 1 abscisses distinctes Exercice 8 (Splines cubiques à peu de nœuds). Soit a = x0 < x2 < ··· < xn = b ...

Chapitre II Interpolation et Approximation

II.22: Spline cubique (`a comparer avec fig. II.1). FIG. II.23: Un dessin en zig-zag (`a gauche) et en splines (`a droite). Théor`eme 8.1 Soit a = x0 < x1

Exercices avec corrigé succinct du chapitre 5

Pour m = 2 le polynôme d'interpolation s'écrit p(t)=1 − t2. On verra plus loin les splines cubiques qui sont également définies par morceaux

Analyse Numérique

interpolation cubique par morceaux de Bessel. Notons que dans ce cas la fonction d ... Exercice 7.5 On reprend la suite {+

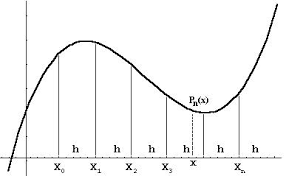Ift 2421 Chapitre 4 Interpolation polynomiale : Collocation

Exercice (suite):. Nous ajoutons un point x F(x). 0. 1. 1. 1. 2. 2. 3. 5. 3 Interpolation par les splines cubiques. Algorithme de résolution de système ...

TP 7 – Splines cubiques – Correction

TP 7 – Splines cubiques – Correction. Exercice 1. a. Pour i = 1 2

feuille dexercices n˚7

Exercice 2 : Interpolation de Hermite. Soit f ∈ C1([a b]

Série dexercices no1/5 Interpolation polynomiale

Exercice 1. Déteminer le polynôme P1 d'interpolation de Lagrange de f aux nœuds 0 et 1. ... Nous appelons spline cubique une fonction S vérifiant.

TD1 : Interpolation et splines

c) Calculer explicitement s dans le cas des nœuds {?2?1

Option B : Examen du 5 Janvier Splines cubiques 1 A propos de l

2 Existence et unicité de la spline cubique contrainte interpolante. On se donne des points x1 < . Corrigé. 1 A propos de l'interpolation de Hermite.

Exercices avec corrigé succinct du chapitre 5

Pour quelle valeur de m le polynôme d'interpolation est unique? On verra plus loin les splines cubiques qui sont également définies par morceaux ...

Réponses aux exercices du chapitre 5

Le polynôme d'interpolation par Lagrange est donné par : a) Obtenir le système linéaire de dimension 3 permettant de calculer la spline cubique.

Série dexercices no1 Interpolation polynomiale

Interpolation polynomiale. Exercice 1. On note Pn ? Rn[X] le polynôme d'interpolation de f ... Nous appelons spline cubique une fonction S vérifiant.

feuille dexercices n?7

2) Déterminer la forme du polynôme d'interpolation de Newton coïncidant avec f Exercice 2 : Interpolation de Hermite. ... Exercice 5 : Splines cubiques.

Exercices corrigés

Exercice 15 On dispose d'un ensemble de n + 1 points (xiyi)

Analyse Numérique

3.1.3 Erreur dans l'interpolation de Lagrange . Ceci prouve l'existence d'une fonction spline cubique à dérivée seconde continue comme.

Interpolation Exercice 1 Exercice 2 Exercice 3 Exercice 4 Exercice 5

Trouver la fonction spline cubique f qui interpole ces données et qui vérifie les conditions f (15) = f (50) = 0. Exercice 8.

TP 7 { Splines cubiques { Correction

Exercice 4 La seule equation pas encore untilis ee est la (7) En remplaceant a i;b i;c i et d i = y i par leurs expressions en fonction de h i;m i et y i on obtient h im i + 2(h i + h i+1)m i+1 + h i+1m i+2 = 6 y i+2 y i+1 h i+1 y i+1 y i h i (12) Exercice 5 En ajoutant les conditions m 1 = 0 et m n = 0 on est amen e a r esoudre le syst eme

Spline — Wikipédia

Figure 2: Piecewise linear interpolation Before we introduce the di?erent kinds of Boundary Conditions we remark there is another approach for obtaining the coe?cients based on Lagrange interpolation! Let g i denote the interpolating cubic on [x ix i+1] and note g?? i is linear

Interpolation Exercice 2 - unistrafr

rouvTer la fonction spline cubique fqui interpole ces données et qui véri e les conditions f0(15) = f0(50) = 0 Exercice 8 Soit une fonction fque l'on cherche à interpoler sur l'intervalle [0;6] (a) Calculer le polynôme d'interpolation Psur les données suivantes x 0 2 4 6 f(x) 0:5 1:7903 3:3900 1:2795 (b) Sachant que la fonction fest

Option B : Examen du 5 Janvier Splines cubiques

Corrigé 1 A propos de l’interpolation de Hermite 1 Comme R 3[X] et R4 ont la même dimension et comme est linéaire il suf?t de véri?er que son noyau est réduit à 0 Or si un polynôme p2R 3[X] est dans le noyau de cela signi?e que p(x g) = p0(x g) = 0; p(x d) = p0(x d) = 0: Ceci montre que x g et x

TP 5 : Interpolation a l’aide de splines cubiques

les points d’interpolation en vue de leur visualisation Le chier cr e e devra contenir a chaque ligne la coordonn ee d’un point t i puis la valeur A i en ce point Testez votre programme avec la fonction fdonn ee en equation (1) et v eri ez que vous avez bien g en er e ce chier

Searches related to interpolation spline cubique exercice corrigé filetype:pdf

Partie II : Interpolation Mth2201A - A08 11 Splines cubiques 11 1 Introduction Probl`eme : • On cherche un interpolant passant par un grand nombre de points d’interpolation (xif(xi)) • Cependant un polynˆomed’interpolation de degr´e´elev´eengendre une erreur importante Id´ee :

Comment fonctionne une spline cubique ?

À droite, une spline cubique dans laquelle les nœuds sont reliés par des polynômes du 3e degré auxquels on a imposé des conditions pour rendre la spline continue au premier degré (les pentes varient de façon continue) et au second degré (la courbure de la spline, plus précisément sa dérivée seconde, varie de façon continue).

Quelle est la différence entre la méthode des splines et l'interpolation polynomiale ?

Dans les problèmes d' interpolation, la méthode des splines est très souvent préférée à l' interpolation polynomiale. Les splines sont également utilisées dans les problèmes de lissage de données expérimentales ou de statistiques. Les splines sont utilisées pour représenter numériquement des contours complexes. Leur mise en œuvre est simple.

Comment calculer les points d’interpolation?

Ce phénomène peut être minimisé en choisissant les points d’interpolation aux nœuds de Tchebychev . Ces points sur un intervalle [a,b] sont définis par la relation suivante : ? ? ? ? ? ? ? = + + ? ? n i xi a b b a

Pourquoi utiliser l’interpolation bicubique ?

La conséquence de cette complexité est que les résultats qu’elle produit sont encore plus lisses et contiennent moins d’artefacts. L’interpolation bicubique est donc finalement l’interpolation la plus utilisée, sauf dans certains cas critiques demandant une grande vitesse d’interpolation.

Exercices avec corrige succinct du chapitre 5

(Remarque: les references ne sont pas gerees dans ce document, par contre les quelques??qui apparaissent dans ce texte sont bien denis dans la version ecran complete du chapitre 5)

Exercice V.1

Soitfune fonction connue aux points d'abscisseti(0in), supposees toutes distinctes. Soit l'ensemblePndes polyn^omes de degre inferieur ou egal an. Tout polyn^omepdePnpeut s'ecrire p(t) =a0+a1t+:::+antn:

On cherchep2 Pntel quep(ti) =f(ti);i= 0;:::;n.

Ecrire les conditions d'interpolation, montrer que le systeme lineaire obtenu admet une solution unique.

Solution :Le probleme s'ecrit:

n X k=0a ktki=f(ti); i= 0;:::;n: C'est donc un systeme lineaire den+ 1 equations an+ 1 inconnues. Ce probleme a une solution unique puisque la matriceMdu systeme (appelee matrice de Van der Monde) est alors inversible. M=0 B

B@1t0::: tn01t1::: tn1::: ::: ::: :::

1tn::: tnn1

CAExercice V.2

On suppose la fonctionfconnue aux pointsf1;0;1gou elle prend les valeursf0;1;0get soitPm l'ensemble des polyn^omes de degre au plusm. Quelle est la valeur minimale demqui conduit a une technique d'interpolation? Pour quelle valeur demle polyn^ome d'interpolation est unique? Solution :On doit avoirm2 car par trois points non alignes on ne peut faire passer une droite! Pourm= 2, le polyn^ome d'interpolation s'ecritp(t) = 1t2. Remarquons que pourm >2, il passe un innite de polyn^omes par trois points.Exercice V.3 On considere les points du planf(ti;zi);0ingavect0< t1< ::: < tn. 1. Ecrire l'equation de la droite passant par les points (ti;zi) et (ti+1;zi+1) en utilisant la base de

Lagrange.

2. Ecrire l'equation de la ligne brisee qui interpole tous les points.

Solution :

1. La droite passant par les points (ti;zi) et (ti+1;zi+1) a pour equationy=gi(t).gis'ecrit:

g i(t) =zitti+1titi+1+zi+1ttiti+1ti: 1

2. La ligne brisee a pour equationy=g(t) ougest une fonction denie par morceau:

g(t) =8 >:g

0(t) pourt2[t0;t1]

1(t) pourt2[t1;t2]

g n1(t) pourt2[tn1;tn] On peut remarquer quegi(ti+1) =gi+1(ti+1) =zi+1, la fonctiongest une fonction continue sur [t0;tn], par contregn'est pas derivable aux pointst1;:::;tn1, en ces points la courbe presente des points anguleux, les derivees a droite et a gauche existent mais sont dierentes. On verra plus loin les splines cubiques qui sont egalement denies par morceaux, mais qui ont plus de regularite.Exercice V.4

Soitnun entier naturel.

1. Calculer l'erreur commise en interpolant la fonctionf(t) =tn, denie sur l'intervalle [0;1], en

les pointsti=i=n,i= 0;1;:::;n, a l'aide du polyn^ome d'interpolation de Lagrange de degren.

Expliquer le resultat.

2. M^eme question pour la fonctiong(t) =tn+1.

Solution :

1. Si l'on applique le resultat sur le calcul d'erreur, on trouve

e(t) = 0 car la derivee d'ordren+ 1 d'un polyn^ome de degrenest nulle. Ce resultat s'explique car par n+ 1 points il passe un polyn^ome et un seul de degren, c'est donctn!

2. Si l'on applique le resultat sur le calcul d'erreur, on trouve

e(t) =1(n+ 1)!(n+ 1)!n(t) =n(t); car la derivee d'ordren+ 1 d'un polyn^ome de degretn+1est (n+ 1)!. On aurait pu retrouver ce resultat directement. Si l'on noteple polyn^ome de degre inferieur ou egal antel quep(ti) =g(ti);i= 0;1;:::;n, alorsgpest un polyn^ome de degre inferieur ou egal an+ 1 qui verie (gp)(ti) = 0, donce(t) = (gp)(t) =(tt0)(tt1):::(ttn), or le coecient detn+1dans le polyn^omegpest 1, donc= 1Exercice V.5

Montrer que les polyn^omes

1;(tt0);(tt0)(tt1);:::;(tt0)(tt1)(ttn1);

forment une base dePn, ensemble des polyn^omes de degre inferieur ou egal an.

Solution :Les polyn^omes etant tous de degre distinct, il est facile de montrer qu'ils sont lineairement

independants. OrPnest un espace vectoriel de dimensionn+ 1. Donc toute famille libre dePnde n+ 1 elements est une base dePn.2

Exercice V.6

On at0= 1;t1= 2;t2= 3,f(t0) = 1;f(t1) = 3;f(t2) = 4. Ecrire le polynomep0de degre 0 qui interpolefent0. Ecrire le polynomep1de degre 1 qui interpolefent0;t1. Ecrire le polynomep2de degre 2 qui interpolefent0;t1;t2. Ecrire chacun des polyn^omes dans la base de Newton.

Solution :On a

0(t) =f(t0) = 1:

On ap1(t) =c0+c1(tt0), on ecrit quep1(t0) =f(t0);p1(t1) =f(t1), on obtient les coecients c

0= 1;c1= 2,

1(t) = 1 + 2(t1):

On ap2(t) =c00+c01(tt0)+c02(tt0)(tt1), onecrit quep2(t0) =f(t0);p2(t1) =f(t1);p2(t2) =f(t2), on obtient les coecientsc00= 1;c01= 2;c03=12, p

2(t) = 1 + 2(t1)12(t1)(t2):

On remarque bien, comme indique dans le paragraphe de cours, que les polyn^omes sont 'emboites' et que pour chaque nouveau polyn^ome il sut de calculer un seul coecient.Exercice V.7 Soit2IR donne, soitpnle polyn^ome de degre inferieur ou egal anqui interpolefent0;t1;:::;tn, on veut evaluer l'erreur en, c'est a direen() =f()pn(). Siest egal a l'un desti, l'erreur est nulle.

Supposons maintenant que6=ti;8i= 0;:::;n.

On denit alors le polyn^omeppar

p(t) =pn(t) + n(t)f()pn()n() ou n(t) =Qn i=0(tti).

1. Montrez quepinterpolefaux pointsft0;t1;:::;tn;g. Quel est le degre dep?

2. En deduirep(t)pn(t) en fonction def[t0;t1;:::;tn;t].

3. En deduire le calcul de l'erreuren() =f()pn().

Solution :

1. Par construction dep, il est facile de montrer quep(ti) =f(ti) pouri= 0;:::;netp() =f().

Le degre de ce polyn^ome est evidemment egal an+ 1.

2. Les proprietes du polyn^ome de Newton donne:

p(t) =pn(t) +f[t0;t1;:::;tn;t]n(t): 3. e n() =f()pn() =p()pn() =f[t0;t1;:::;tn;]n(): 3

Exercice V.8

Soit la fonctionfconnue aux trois points d'abscisset0,t1ett2. On considere le polyn^ome d'interpo- lation dans la base de Newton avec les notations du cours. Montrer, par le calcul, que c

2=f[t0;t1;t2]

en utilisant la denition et la symetrie des dierences divisees.

Solution :Le polyn^ome s'ecrit

p(t) =c0+c1(tt0) +c2(tt0)(tt1): Or p(t0) =f(t0))c0=f[t0] p(t1) =f(t1))c1=f(t1)f(t0)t1t0=f(t0)f(t1)t0t1=f[t0;t1] p(t2) =f(t2))c2=f(t2)f(t0)t2t0f[t0;t1]t2t1=f[t2;t0]f[t0;t1]t2t1=f[t2;t0;t1] =f[t0;t1;t2] On a utilise la symetrie des dierences divisees.Exercice V.9 Calculer les coecientsckdu polyn^ome d'interpolationp3de l'exemple??, dans la base de Newton. Solution :Pour calculer les coefcients dep3(t) dans la base deNewton, nous sommes conduits a construire le tableau propose dans le cours pourn= 3, ce qui avec les donnees de l'exercice nous

donne:k= 0k= 1k= 2k= 3t0= 0f[t0] =12t1= 1f[t1] = 1f[t0;t1] =12t2= 2f[t2] = 2f[t1;t2] = 1f[t0;t1;t2] =14t3= 3f[t3] =12f[t2;t3] =52f[t1;t2;t3] =74f[t0;t1;t2;t3] =23On peut donc ecrirep3(t) de la facon suivante:

3(t) =12+12t+14t(t1)23t(t1)(t2):Exercice V.10

On a calcule a l'aide des dierences divisees le polyn^omepnd'interpolation defaux pointsft0;:::;tng.

On desire rajouter un point d'interpolationtn+1. Doit-on refaire tout le tableau des dierences divisees?

Et, si on utilisait la base des polyn^omes de Lagrange, devrait-on refaire tous les calculs? Solution :Si vous avez compris les calculs eectues dans le tableau des dierences divisees du 4 paragraphe??, il sut d'ajouter une ligne a ce tableau pour ajouter un point d'interpolation. Les coecientsfc0;:::;cngsont les m^emes que ceux depnle dernier coecient de la derniere ligne donnera c

n+1. Si les calculs ont ete faits a la main, vous les avez evidemment gardes. Par contre, si vous avez

utilise l'algorithme donne dans le m^eme paragraphe, une colonne se superpose a la precedente, et le tableau complet n'est donc pas garde en memoire. Il faut donc penser a stocker le tableau ... En ce qui concerne la base des polyn^omes de Lagrange, chacun d'eux est construit a partir de tous

les points d'interpolation, ce qui necessite de recalculer tous ces polyn^omes lorsque l'on rajoute un

point d'interpolation!Exercice V.11 Calculer le nombre d'operations arithmetiques necessaires pour evaluer, en un pointt, la valeur de p n(t) =c0+c1(tt0) +c2(tt0)(tt1) +:::+cn(tt0)(tt1):::(ttn1):

1. Par la methode `naturelle', en ecrivant l'algorithme

2. Par le schema de Horner.

Solution :

1. L'algorithme "classique" est le suivant:

1:Les donnees sont:c0;:::;cn;t0;:::;tn1;t

2:q=tt0

3:p=c0+c1q

4:pourk= 2 jusqu'anfaire

5:q=q(ttk1)

6:p=p+ckq

7:n pour

Ceci correspond a 2n1 multiplications,nadditions etnsoustractions.

2. Le schema de Horner, dont l'algorithme est donne dans le cours comptenmultiplications,n

additions etnsoustractions.Exercice V.12

Mettre en evidence experimentalement, en utilisant un logiciel de calcul (Matlab, Scilab,...) les di-

cultes de l'interpolation polynomiale de la fonction 1=(1 +t2) sur l'intervalle [5;+ 5].

Exercice V.13

1. Compter le nombre de degres de liberte a determiner pour denir completement une spline

cubique.

2. Compter le nombre d'equations disponibles pour ce faire. Comparer.

Solution :Sur chacun desnintervalles [ti;ti+1];i= 0;:::;n1,gest un polyn^ome de degre inferieur ou egal a 3, on a doncg(t) =i+it+ it2+it3, il y a donc 4ninconnues.

On doit avoir

g(t+i) =g(ti);g0(t+i) =g0(ti);g00(t+i) =g00(ti);i= 1;:::;n1 an que la fonctiongsoit 2 fois contin^ument derivable. On obtient donc 3(n1) equations. 5 La fonctiongdoit interpoler, on doit donc avoirg(ti) =yi;i= 0;:::;n.

On a donc au total 3n3 +n+ 1 = 4n2 equations.

Il manque donc deuxequations, c'est pourquoi on impose, par exemple, les conditions supplementaires: g

00(t0) =g00(tn) = 06

quotesdbs_dbs12.pdfusesText_18

[PDF] Exercices avec corrigé succinct du chapitre 5

Comment fonctionne une spline cubique ?

Quelle est la différence entre la méthode des splines et l'interpolation polynomiale ?

Comment calculer les points d’interpolation?

Pourquoi utiliser l’interpolation bicubique ?

Exercices avec corrige succinct du chapitre 5

Exercice V.1

On cherchep2 Pntel quep(ti) =f(ti);i= 0;:::;n.

Solution :Le probleme s'ecrit:

B@1t0::: tn01t1::: tn1::: ::: ::: :::

1tn::: tnn1

CAExercice V.2

Lagrange.

Solution :

1. La droite passant par les points (ti;zi) et (ti+1;zi+1) a pour equationy=gi(t).gis'ecrit:

2. La ligne brisee a pour equationy=g(t) ougest une fonction denie par morceau:

0(t) pourt2[t0;t1]

1(t) pourt2[t1;t2]

Soitnun entier naturel.

1. Calculer l'erreur commise en interpolant la fonctionf(t) =tn, denie sur l'intervalle [0;1], en

Expliquer le resultat.

2. M^eme question pour la fonctiong(t) =tn+1.

Solution :

1. Si l'on applique le resultat sur le calcul d'erreur, on trouve

2. Si l'on applique le resultat sur le calcul d'erreur, on trouve

Montrer que les polyn^omes

1;(tt0);(tt0)(tt1);:::;(tt0)(tt1)(ttn1);

Exercice V.6

Solution :On a

0(t) =f(t0) = 1:

0= 1;c1= 2,

1(t) = 1 + 2(t1):

2(t) = 1 + 2(t1)12(t1)(t2):

Supposons maintenant que6=ti;8i= 0;:::;n.

On denit alors le polyn^omeppar

1. Montrez quepinterpolefaux pointsft0;t1;:::;tn;g. Quel est le degre dep?

2. En deduirep(t)pn(t) en fonction def[t0;t1;:::;tn;t].

3. En deduire le calcul de l'erreuren() =f()pn().

Solution :

1. Par construction dep, il est facile de montrer quep(ti) =f(ti) pouri= 0;:::;netp() =f().

2. Les proprietes du polyn^ome de Newton donne:

Exercice V.8

2=f[t0;t1;t2]

Solution :Le polyn^ome s'ecrit

3(t) =12+12t+14t(t1)23t(t1)(t2):Exercice V.10

1. Par la methode `naturelle', en ecrivant l'algorithme

2. Par le schema de Horner.

Solution :

1. L'algorithme "classique" est le suivant:

1:Les donnees sont:c0;:::;cn;t0;:::;tn1;t

2:q=tt0

3:p=c0+c1q

4:pourk= 2 jusqu'anfaire

5:q=q(ttk1)

6:p=p+ckq

7:n pour

2. Le schema de Horner, dont l'algorithme est donne dans le cours comptenmultiplications,n

Exercice V.13

1. Compter le nombre de degres de liberte a determiner pour denir completement une spline

2. Compter le nombre d'equations disponibles pour ce faire. Comparer.

On doit avoir

On a donc au total 3n3 +n+ 1 = 4n2 equations.

00(t0) =g00(tn) = 06