 Méthodes numériques de résolution déquations différentielles
Méthodes numériques de résolution déquations différentielles
Les fonctions. Matlab (Octave) pour résoudre une équation différentielle ne marchent pas si la fonction retourne un vecteur ligne. L'écriture de la fonction '
 Résolution dune équation différentielle non linéaire Léquation de
Résolution dune équation différentielle non linéaire Léquation de
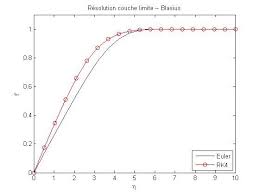
21 fév. 2012 Puis une comparaison des résultats est faite avec ceux obtenus par la routine Matlab® ode45 (type Runge Kutta ordre 4/5). On remarque que dans ...
 Untitled
Untitled
On voit donc que la réponse totale pour cette équation est la somme des réponses libre et forcée. Equations non linéaires. Les équations différentielles non
 Résolution numérique des équations différentielles ordinaires
Résolution numérique des équations différentielles ordinaires
L'équation différentielle est non-linéaire lorsque les coefficients dépendent de u et/ou de ses dérivées. Lors de la résolution analytique des équations
 Méthodes numériques pour les systèmes dynamiques non linéaires
Méthodes numériques pour les systèmes dynamiques non linéaires
16 oct. 2012 la non-linéarité non polynômiale en une équation différentielle ordinaire quadra- ... Floquet : Sur les équations différentielles linéaires à ...
 TP n°1 : Introduction au Systèmes Non linéaires « Pendule simple
TP n°1 : Introduction au Systèmes Non linéaires « Pendule simple
g l ω = . Cependant il existe des méthodes permettant de résoudre l'équation différentielle non linéaire Matlab pour les différentes valeurs initiales ...
 TP n°1 : Introduction au Systèmes Non linéaires « Pendule simple
TP n°1 : Introduction au Systèmes Non linéaires « Pendule simple
g l ω = . Cependant il existe des méthodes permettant de résoudre l'équation différentielle non linéaire Matlab pour les différentes valeurs initiales ...
 Méthodes numériques de résolution déquations différentielles
Méthodes numériques de résolution déquations différentielles
ª Equation différentielle non linéaire. Calcul de la solution par séparation ª équation différentielle d'ordre 2 non linéaire. Pendule pesant non amorti ...
 Modèle de rapport sur le projet Étude de leffet de la linéarisation du
Modèle de rapport sur le projet Étude de leffet de la linéarisation du
7 jan. 2016 Cependant il existe des méthodes permettant de résoudre l'équation différentielle non linéaire ... 1 Solution approchée des équations ...
 Résolution déquations différentielles avec Matlab
Résolution déquations différentielles avec Matlab
pas de temps dt est donc en code Matlab : t = t0:dt:tf;. % on fixe la grille de ... Ici
 Résolution dune équation différentielle non linéaire Léquation de
Résolution dune équation différentielle non linéaire Léquation de
21 févr. 2012 Cet article présente une méthode de résolution sous Matlab d'une équation différentielle non linéaire et possédant une condition de bout.
 TP n°1 : Introduction au Systèmes Non linéaires « Pendule simple
TP n°1 : Introduction au Systèmes Non linéaires « Pendule simple
enseigne plutôt l'équation différentielle linéaire " de manière approchée MATLAB fournit de telles méthodes. ... Etude du système par Matlab.
 Présentation de Matlab 1. Introduction - Historique 2. Démarrage de
Présentation de Matlab 1. Introduction - Historique 2. Démarrage de
Résolution d'équations et de Systèmes d'équations non Linéaire Résolution numérique des équations différentielles et des équations aux dérivées ...
 Méthodes numériques pour les systèmes dynamiques non linéaires
Méthodes numériques pour les systèmes dynamiques non linéaires
16 oct. 2012 système d'équations algébriques non linéaires dont les solutions sont calculées ... MATLAB. Outre une interface graphique plus conviviale
 Résolution déquations aux dérivées partielles non linéaires et
Résolution déquations aux dérivées partielles non linéaires et
2.2 Exemple de résolution `a l'aide de la PDE Toolbox sous Matlab . équations différentielles non linéaires couplées `a un probl`eme de point fixe ...
 Modélisation dun contact dynamique non-linéaire: application au
Modélisation dun contact dynamique non-linéaire: application au
27 mars 2012 Le sujet relève de la tribologie et de l'analyse non-linéaire du ... l'exemple de cette équation différentielle linéaire du second ordre :.
 Résolution numérique des équations différentielles ordinaires
Résolution numérique des équations différentielles ordinaires
Programmation par le logiciel Matlab (Méthodes Numériques S1) L'équation différentielle est non-linéaire lorsque les coefficients dépendent de u et/ou ...
 Initiation à Matlab ESSTIN - Université de Lorraine
Initiation à Matlab ESSTIN - Université de Lorraine
5.2 Recherche de zéros d'une fonction non linéaire . 6.2 Equation différentielle d'ordre 2 et suspension d'une voiture . . . . . . . . . . . 48.
 Matlab pour les ingénieurs Quelques exemples
Matlab pour les ingénieurs Quelques exemples
Cette introduction à Matlab est proposée aux étudiants du département que son mouvement est décrit par une équation différentielle non-linéaire d'ordre ...
 Méthodes numériques de résolution déquations différentielles
Méthodes numériques de résolution déquations différentielles
Matlab (Octave) pour résoudre une équation différentielle ne marchent pas si des modélisations plus réalistes (ex. forces de frottement non-linéaires) ...
 EN40 Matlab Tutorial - Brown University
EN40 Matlab Tutorial - Brown University
Solving ordinary differential equations (ODEs) using MATLAB 11 1 Solving a basic differential equation 11 2 Solving a basic differential equation in an M-file 11 3 Solving a differential equation with adjustable parameters 11 4 Common errors 11 5 Solving simultaneous differential equations 11 6
 Chapitre 3 Résolution numérique des équations non linéaires
Chapitre 3 Résolution numérique des équations non linéaires
de signe opposé en a et b elle s’annule entre les deux Écrivons un script matlab élémentaire function [cnit]= dicho(fab) dicho calcule un zéro de la fonction f dans l’intervalle [ab] au moyen de la méthode de dichotomie juqu’à la précision machine c=(a+b)/2; nit=0; 1
 Equations Differentielles´ - École Polytechnique
Equations Differentielles´ - École Polytechnique
2 Montrer que le changement de variable x1= rcos?et x2= rsin?permet de r´eecrire le syst´ `eme diff ´erentiel non lin eaire sous la forme´ r? = µr(1?r2) ?? = ?1 Integrer ce syst´ `eme avec les conditions initiales r= r0?= ?0et montrer qu’il admet la solution r2(t) = r2 0 r2 0+(1?r2 0) e?2µt ?(t) = ?0?t 3
 Searches related to matlab equation différentielle non linéaire PDF
Searches related to matlab equation différentielle non linéaire PDF
Chap 1 : Résolution d'équations non-linéaires But : Recherche des solutions de l'équation non linéaire f(x) = 0 où f est une fonction donnée! Les méthodes numériques pour approcher une solution consistent à localiser grossièrement un zéro de f en procédant le plus souvent par des consi-
How to solve a differential equation using MATLAB®?
This example shows how to use MATLAB® to formulate and solve several different types of differential equations. MATLAB offers several numerical algorithms to solve a wide variety of differential equations: d 2 y d t 2 - ? ( 1 - y 2) d y d t + y = 0. function dydt = vanderpoldemo (t,y,Mu) %VANDERPOLDEMO Defines the van der Pol equation for ODEDEMO.
How do you solve a nonlinear differential equation?
Solve the equation with the initial condition y (0) == 2. The dsolve function finds a value of C1 that satisfies the condition. If dsolve cannot solve your equation, then try solving the equation numerically. See Solve a Second-Order Differential Equation Numerically. Solve this nonlinear differential equation with an initial condition.
How to solve van der Pol equation in MATLAB?
The equation is written as a system of two first-order ordinary differential equations (ODEs). These equations are evaluated for different values of the parameter ?. For faster integration, you should choose an appropriate solver based on the value of ?. For ? = 1, any of the MATLAB ODE solvers can solve the van der Pol equation efficiently.
AIX-MARSEILLE UNIVERSITÉ
ÉCOLE DOCTORALE SCIENCES POUR L"INGÉNIEUR :
MÉCANIQUE, PHYSIQUE, MICRO ET NANOÉLECTRONIQUE (ED 353)THÈSE
Pour obtenir le grade de
DOCTEUR DE L"UNIVERSITÉ D"AIX-MARSEILLE
Discipline : Acoustique
Soutenue publiquement le 10 janvier 2012 par
Sami KARKAR
Méthodes numériques pour les systèmes
dynamiques non linéairesApplication aux instruments de musique
auto-oscillantsJURY : Dr. Joël GILBERT Président
Pr. Gaëtan KERSCHEN Rapporteur
Dr. Cyril TOUZÉ Rapporteur
Pr. José ANTUNES Examinateur
Pr. Marc MÉDALE Examinateur
Pr. Bruno COCHELIN Directeur de thèse
Dr. Christophe VERGEZ Co-directeur de thèse
LABORATOIRE DE MÉCANIQUE ET D"ACOUSTIQUE - C.N.R.S. (UPR 7051)Résumé
Ces travaux s"articulent autour du calcul des solutions périodiques dans les sys- tèmes dynamiques non linéaires, au moyen de méthodes numériques de continuation. La recherche de solutions périodiques se traduit par un problème avec condi- tions aux limites périodiques, pour lequel nous avons implémenté deux méthodes d"approximation : - Une méthode spectrale dans le domaine fréquentiel : l"équili- brage harmonique d"ordre élevé, qui repose sur une formulation quadratique des équations. Nous proposons en outre une formulation originale permettant d"étendre cette méthode aux cas de non-linéarités non rationnelles. -Une méthode pseudo- spectrale par éléments dans le domaine temporel : la collocation à l"aide fonctions polynômiales par morceaux. Ces méthodes transforment le problème continu en un système d"équations algébriques non linéaires, dont les solutions sont calculées par continuation à l"aide de la méthode asymptotique numérique. L"ensemble de ces outils, intégrés au code de calcul MANLAB et complétés d"uneanalyse linéaire de stabilité, sont alors utilisés pour l"étude des régimes périodiques
d"une classe particulière de systèmes dynamiques non linéaires : les instruments de musique auto-oscillants. Un modèle physique non-régulier de clarinette est étudié endétail : à partir de la branche de solutions statiques et ses bifurcations, on calcule les différentes branches de solutions périodiques, ainsi que leur stabilité et leursbifurcations. Ce modèle est ensuite adapté au cas du saxophone, pour lequel on intègre une caractérisation acoustique expérimentale, afin de mieux tenir compte de la géométrie complexe de l"instrument. Enfin, nous étudions un modèle physique simplifié de violon, avec une non-régularité liée frottement de Coulomb. Cette dernièreapplication illustre ainsi la polyvalence des outils développés face aux différents types de non-régularité.Table des matièresRésumé4
Avant-propos11
Introduction13
I Systèmes dynamiques et méthodes numériques 191 Systèmes dynamiques21
1.1 Système dynamique . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.1.1 Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.1.2 Trajectoires, solutions . . . . . . . . . . . . . . . . . . . . . . 22
1.2 Solutions statiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1.2.1 Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1.2.2 Branche de solutions statiques . . . . . . . . . . . . . . . . . . 23
1.2.3 Stabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1.2.4 Bifurcations des solutions statiques . . . . . . . . . . . . .. . 24
1.3 Solutions périodiques . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.3.1 Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.3.2 Branche de solutions périodiques . . . . . . . . . . . . . . . . 26
1.3.3 Stabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.3.4 Analogie avec les systèmes discrets ou " cartes » . . . . .. . . 28
1.3.5 Bifurcations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
1.4 Bifurcations des régimes instables . . . . . . . . . . . . . . . . .. . . 29
1.4.1 Solutions statiques . . . . . . . . . . . . . . . . . . . . . . . . 29
1.4.2 Solutions périodiques . . . . . . . . . . . . . . . . . . . . . . . 29
1.5 Systèmes non réguliers . . . . . . . . . . . . . . . . . . . . . . . . . . 30
2 Méthodes numériques de continuation 31
2.1 La continuation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.1.1 Exemple simple . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.2 Méthodes prédicteur-correcteur . . . . . . . . . . . . . . . . . . .. . 32
2.2.1 Principe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.2.2 Prédicteur tangent . . . . . . . . . . . . . . . . . . . . . . . . 33
2.2.3 Correction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
2.2.4 Itération . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
6TABLE DES MATIÈRES
2.2.5 Pilotage des méthodes MPC . . . . . . . . . . . . . . . . . . . 35
2.3 Méthode Asymptotique Numérique . . . . . . . . . . . . . . . . . . . 35
2.3.1 Principe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
2.3.2 Systèmes linéaires en cascade . . . . . . . . . . . . . . . . . . 36
2.3.3 Taille du pas . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
2.3.4 Itération . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.3.5 Correction éventuelle . . . . . . . . . . . . . . . . . . . . . . . 39
2.4 MANLAB : une implémentation originale de la MAN . . . . . . . .. 39
3 Méthodes de discrétisation des solutions périodiques 41
3.1 Méthodes de discrétisation . . . . . . . . . . . . . . . . . . . . . . . .42
3.1.1 Du continu au discret . . . . . . . . . . . . . . . . . . . . . . . 42
3.1.2 Méthodes spectrales . . . . . . . . . . . . . . . . . . . . . . . 43
3.2 Méthode de l"Équilibrage Harmonique . . . . . . . . . . . . . . . .. 44
3.2.1 Fonctions de représentation . . . . . . . . . . . . . . . . . . . 45
3.2.2 Fonctions test . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
3.2.3 Équation de phase . . . . . . . . . . . . . . . . . . . . . . . . 45
3.2.4 Systèmes quadratiques . . . . . . . . . . . . . . . . . . . . . . 46
3.2.5 Cas particulier des systèmes non autonomes . . . . . . . . .. 46
3.2.6 Implémentation dans MANLAB . . . . . . . . . . . . . . . . . 47
3.3 Collocation orthogonale aux points de Gauss . . . . . . . . . .. . . . 47
3.3.1 Fonctions de représentation . . . . . . . . . . . . . . . . . . . 47
3.3.2 Base de projection . . . . . . . . . . . . . . . . . . . . . . . . 48
3.3.3 Implémentation dans MANLAB . . . . . . . . . . . . . . . . . 49
3.A Annexes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
3.A.1 Matrice A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
3.A.2 Matrice B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.A.3 Matrice B" . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
4 Optimisation des temps de calcul55
4.1 Temps de calcul peu optimisés . . . . . . . . . . . . . . . . . . . . . . 56
4.1.1 Calcul de la matrice tangente . . . . . . . . . . . . . . . . . . 56
4.2 Compilation d"une partie du code . . . . . . . . . . . . . . . . . . . .58
4.2.1 Principe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
4.2.2 Performances . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.3 Approche tenseurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.3.1 Principe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
4.3.2 Calcul des tenseursL0,L, etQ. . . . . . . . . . . . . . . . . . 60
4.3.3 Forme tensorielle des équations continues . . . . . . . . .. . . 60
4.3.4 Tenseurs pour l"équilibrage harmonique . . . . . . . . . . .. . 61
4.3.5 Tenseurs pour la collocation polynômiale . . . . . . . . . .. . 63
4.3.6 Écriture matricielle . . . . . . . . . . . . . . . . . . . . . . . . 65
4.4 Comparaison des approches . . . . . . . . . . . . . . . . . . . . . . . 66
TABLE DES MATIÈRES7
5 Traitement des non-linéarités non polynômiales 69
5.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
5.2 An introductive example . . . . . . . . . . . . . . . . . . . . . . . . . 72
5.2.1 First-order recast . . . . . . . . . . . . . . . . . . . . . . . . . 72
5.2.2 Quadratic recast of the exponential function . . . . . . .. . . 72
5.2.3 Applying the harmonic balance method to the ODEs . . . . .73
5.2.4 Recast of the non linear algebraic equation . . . . . . . . .. . 74
5.2.5 Periodic solutions of the regularised vibro-impact .. . . . . . 75
5.3 General treatment of nonlinear functions . . . . . . . . . . . .. . . . 76
5.3.1 First order derivative . . . . . . . . . . . . . . . . . . . . . . . 76
5.3.2 Second order derivative . . . . . . . . . . . . . . . . . . . . . . 76
5.4 Recast of a few common non-polynomial nonlinearities . .. . . . . . 77
5.4.1 Natural logarithm . . . . . . . . . . . . . . . . . . . . . . . . . 77
5.4.2 Non-integer power . . . . . . . . . . . . . . . . . . . . . . . . 77
5.4.3 Trigonometric functions . . . . . . . . . . . . . . . . . . . . . 77
5.5 Periodic solutions of the nonlinear pendulum . . . . . . . . .. . . . . 78
5.6 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
5.A Vibro-impact system . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
5.A.4 Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
5.A.5 Recast of conservative systems . . . . . . . . . . . . . . . . . . 81
5.B Quadratic framework . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
5.C Extended framework . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
5.C.6 Series computation . . . . . . . . . . . . . . . . . . . . . . . . 81
5.C.7 Implementation in MANLAB . . . . . . . . . . . . . . . . . . 82
6 Comparaison entre HBM et collocation 85
6.1 Système non linéaire à deux ressorts . . . . . . . . . . . . . . . . .. 86
6.1.1 Modélisation . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
6.1.2 Paramètre de continuation . . . . . . . . . . . . . . . . . . . . 87
6.1.3 Forme quadratique du premier ordre . . . . . . . . . . . . . . 87
6.1.4 Étude de convergence . . . . . . . . . . . . . . . . . . . . . . . 88
6.1.5 Continuation des solutions périodiques . . . . . . . . . . .. . 89
6.2 Le système vibro-impact régularisé . . . . . . . . . . . . . . . . .. . 93
6.2.1 Modélisation . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
6.2.2 Paramètre de continuation . . . . . . . . . . . . . . . . . . . . 93
6.2.3 Étude de convergence . . . . . . . . . . . . . . . . . . . . . . . 93
6.2.4 Continuation des solutions périodiques . . . . . . . . . . .. . 99
6.3 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
II Application à l"acoustique musicale 103
7 Modélisation des instruments de musique à anche simple 105
7.1 Principe général de fonctionnement . . . . . . . . . . . . . . . . .. . 106
7.2 Mécanique de l"anche . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
7.2.1 Modélisation du contact . . . . . . . . . . . . . . . . . . . . . 107
7.3 Acoustique du résonateur . . . . . . . . . . . . . . . . . . . . . . . . . 108
8TABLE DES MATIÈRES
7.3.1 Modèle analytique du cylindre . . . . . . . . . . . . . . . . . . 109
7.3.2 Modèle analytique du tronc de cône . . . . . . . . . . . . . . . 109
7.3.3 Caractérisation expérimentale . . . . . . . . . . . . . . . . . .109
7.3.4 Décomposition modale . . . . . . . . . . . . . . . . . . . . . . 110
7.3.5 Équations dans le domaine temporel . . . . . . . . . . . . . . 110
7.4 Couplage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
7.5 Équations adimensionnées . . . . . . . . . . . . . . . . . . . . . . . . 112
7.6 Reformulation quadratique . . . . . . . . . . . . . . . . . . . . . . . .112
7.6.1 Équation du débit . . . . . . . . . . . . . . . . . . . . . . . . 113
7.6.2 Effort de contact . . . . . . . . . . . . . . . . . . . . . . . . . 113
7.6.3 Système complet . . . . . . . . . . . . . . . . . . . . . . . . . 113
8 Régimes périodiques de la clarinette 115
8.1 Paramètres et régularisation du modèle . . . . . . . . . . . . . .. . . 116
8.1.1 Nombre de modes acoustiques . . . . . . . . . . . . . . . . . . 116
8.1.2 Valeurs des paramètres . . . . . . . . . . . . . . . . . . . . . . 117
8.2 Branche statique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
8.2.1 Calcul analytique . . . . . . . . . . . . . . . . . . . . . . . . . 118
8.2.2 Continuation de point fixe : équilibrage harmonique à l"ordre 0 120
8.2.3 Calcul à l"aide du logiciel AUTO . . . . . . . . . . . . . . . . 121
8.2.4 Retour sur la modélisation du contact . . . . . . . . . . . . . .122
8.3 Régimes périodiques . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
8.3.1 Premiers résultats . . . . . . . . . . . . . . . . . . . . . . . . . 122
8.3.2 Problèmes numériques liés au contact . . . . . . . . . . . . . .123
8.3.3 Influence des régularisations sur la stabilité . . . . . .. . . . . 127
8.3.4 Estimation du nombre d"harmoniques nécessaires . . . .. . . 128
8.3.5 Calcul du premier registre . . . . . . . . . . . . . . . . . . . . 130
8.3.6 Stabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
8.4 Autres régimes périodiques . . . . . . . . . . . . . . . . . . . . . . . .139
9 Régimes périodiques du saxophone 145
9.1 Impédance d"entrée . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
9.2 Rappels sur le modèle . . . . . . . . . . . . . . . . . . . . . . . . . . 146
9.3 Branche statique : stabilité et bifurcations . . . . . . . . .. . . . . . 147
9.4 Régimes périodiques . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
9.4.1 Première branche périodique . . . . . . . . . . . . . . . . . . . 148
9.4.2 Diagramme de bifurcation en pression et stabilité . . .. . . . 148
9.4.3 Fréquence de jeu . . . . . . . . . . . . . . . . . . . . . . . . . 150
10 Régimes périodiques du violon153
10.1 Modèle simplifié de violon . . . . . . . . . . . . . . . . . . . . . . . . 153
10.1.1 Régularisation du frottement de Coulomb . . . . . . . . . .. 154
10.1.2 Système du premier ordre . . . . . . . . . . . . . . . . . . . . 156
10.1.3 Formulation quadratique . . . . . . . . . . . . . . . . . . . . . 156
10.1.4 Analyse du régime statique . . . . . . . . . . . . . . . . . . . 157
10.2 Analyse numérique . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158
10.2.1 Adimensionnement . . . . . . . . . . . . . . . . . . . . . . . . 158
TABLE DES MATIÈRES9
10.2.2 Branche statique . . . . . . . . . . . . . . . . . . . . . . . . . 159
10.3 Régime périodique du violon . . . . . . . . . . . . . . . . . . . . . . .160
10.3.1 Calcul par équilibrage harmonique et MAN . . . . . . . . . .160
10.3.2 Calcul par collocation . . . . . . . . . . . . . . . . . . . . . . 161
11 Seuils d"oscillation de la clarinette : une approche par continuation165
11.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
11.2 Physical model of single reed instruments . . . . . . . . . . .. . . . . 168
11.2.1 Dynamics of the reed . . . . . . . . . . . . . . . . . . . . . . . 168
11.2.2 Acoustics of the resonator . . . . . . . . . . . . . . . . . . . . 169
11.2.3 Nonlinear coupling . . . . . . . . . . . . . . . . . . . . . . . . 170
11.2.4 Reed motion induced flow . . . . . . . . . . . . . . . . . . . . 170
11.2.5 Global flow . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
11.2.6 Dimensionless model . . . . . . . . . . . . . . . . . . . . . . . 171
11.3 Methods : Theoretical principles and numerical tools .. . . . . . . . 172
11.3.1 Branch of static solutions . . . . . . . . . . . . . . . . . . . . 172
11.3.2 Continuation of static solutions . . . . . . . . . . . . . . . .. 172
11.3.3 Hopf Bifurcation . . . . . . . . . . . . . . . . . . . . . . . . . 172
11.3.4 Branch and continuation of Hopf bifurcations . . . . . .. . . 173
11.4 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173
11.4.1 Reed-bore interaction . . . . . . . . . . . . . . . . . . . . . . . 176
11.4.2 Simultaneous influence of reed damping and modal frequency . 177
11.4.5 Influence of the reed motion induced flow . . . . . . . . . . . .186
11.5 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
Conclusion Générale193
Bibliographie197
10TABLE DES MATIÈRES
Avant-propos
Ce document présente les travaux que j"ai réalisés au cours de mes trois années de thèse au sein de l"équipe Signaux Sonores et Musicaux d"une part, et de l"équipe Méthodes Numériques d"autre part, au Laboratoire de Mécanique et d"Acoustique (LMA), unité propre de recherche du CNRS. Ces travaux ont étédirigés conjointe- ment par Bruno Cochelin et Christophe Vergez. Ils ont été financés à parts égales par le CNRS et la DGA. "Il avait dit: - Tel jour cet astre reviendra.-Il mourut.
L"ombre est vaste et l"on n"en parla plus
[...] On oublia le nom,L"homme, tout; ce rêveur digne du cabanon,
Ces calculs poursuivant, dans leur vagabondage
Des astres qui n"ont point d"orbite et n"ont point d"âge,Ces Soleils à travers les chiffres aperçus;
Et la ronce se mit à pousser là-dessus. [...]On vivait. [...]
Et depuis bien longtemps personne ne pensait
Au pauvre vieux rêveur enseveli sous l"herbe.
Soudain, un soir, on vit la nuit noire et superbe, [...] Blêmir confusément, puis blanchir, et c"était Dans l"année annoncée et prédite, et la cimeDes monts eut un reflet étrange de l"abîme
Comme lorsqu"un flambeau rôde derrière un mur,Et la blancheur devint lumière, et dans l"azur
La clarté devint pourpre, et l"on vit poindre, éclore, Et croître on ne sait quelle inexprimable auroreQui se mit à monter dans le haut firmament
Par degrés et sans hâte et formidablement; [...]Et soudain, comme un spectre entre en une maison,
Apparut, par-dessus le farouche horizon,
Une flamme emplissant des millions de lieues,
Monstrueuse lueur des immensités bleues,
Splendide au fond du ciel brusquement éclairci; Et l"astre effrayant dit aux hommes : " Me voici! »" Victor Hugo, " La Comète », La légende des siècles. Introduction GénéralePériodicité et oscillations spontanées Qu"est-ce qu"un phénomène périodique? Est-ce, comme on le présente habituel- lement, " un phénomène qui se répète à intervalles de temps réguliers, et dont on peut mesurer la principale caractéristique : la période »? Ou est-ce le phénomène périodique qui permet justement, par sa période, demesurerle temps? De l"apparition tous les 76 ans de la comète de Halley aux oscillations à 4MHz d"un cristal de quartz, en passant par le rythme circadien des cyanobactéries, ou encore les différents cycles saisonniers du climat... Toutes ces horloges sont des oscil- lateurs qui mesurent le temps. Pour le physicien, ce sont dessystèmes dynamiques. Dans certains cas, les oscillations apparaissent spontanément, sans qu"aucun agent extérieur ne viennent imposer cette périodicité au système : on parle de systèmeautonome. Ainsi, un objet cylindrique soumis à un écoulement uniforme provoque un sillage oscillant (allée de von Karmann) qui, enretour, interagit avec l"objet qui se met alors à osciller. De même, un frein à disqueautomobile soumis à un effort constant peut faire naître, du frottement, une oscillation audible : le crissement. C"est par ailleurs le même phénomène qui explique le son d"un violon dont on frotte une corde avec un archet. Enfin, une clarinetteest capable d"émettre une note, c"est-à-dire une oscillation de pression, alors que le souffle du musicien est continu. Dans tous ces exemples, l"apparition des oscillations est spontanée. Et dans cha- cun de ces exemples, c"est un phénomènenon linéairequi permet de l"expliquer.Ainsi, le caractère non linéaire joue un rôle prépondérant dans l"étude des oscilla-
teurs, comme le sont les instruments de musique auto-oscillants.De la physique des instruments de musique...
Un instrument de musique peut se décomposer en un phénomène d"excitation (souffle du musicien dans l"embouchure d"un instrument à vent, frottement de l"ar- chet sur la corde d"un violon, impact d"une baguette sur une peau...), couplé à un phénomène de résonance. Le type d"excitation permet de distinguer deux catégories d"instruments : - les instruments à oscillations libres, dont l"excitationest de type impulsionnel (percussions, cordes frappées ou pincées); - les instruments à oscillations auto-entretenues, ou encoreauto-oscillants, dont l"excitation est continue (comme les vents et les cordes frottées).14INTRODUCTION
Fig.1 - Schéma de principe du fonctionnement d"un instrument auto-oscillant. La partie résonante de l"instrument est elle-même composéede deux éléments : le résonateur qui réalise un filtrage sélectif de cette excitation (colonne d"air, corde vibrante, caisse de résonance), et un élément qui permet de transmettre les vibra- tions dans le milieu ambiant sous forme de rayonnement acoustique (pavillon, table d"harmonie, membrane). Les instruments auto-oscillants fonctionnent donc comme un oscillateur clas- sique : l"énergie est injectée sous forme quasi-statique (àl"échelle de temps d"une note), un couplage à l"aide d"un élément non linéaire permetde transformer une partie de cette énergie sous forme d"oscillations, et un élément linéaire fortement résonant permet de " sélectionner » une fréquence particulière de fonctionnement (voir la figure 1). Du point de vue de la physique, ce type d"instrument peut êtremodélisé parquotesdbs_dbs27.pdfusesText_33[PDF] faire de sa vie une oeuvre d'art foucault
[PDF] test de personnalité recrutement gratuit pdf
[PDF] fais de ta vie une oeuvre dart citation
[PDF] faire de sa vie une oeuvre d'art citation
[PDF] test de personnalité gratuit avec résultat pdf
[PDF] toute conscience est conscience de quelque chose
[PDF] test personnalité pdf
[PDF] il faut faire de sa vie une oeuvre d'art citation
[PDF] qui a dit il faut faire de sa vie une oeuvre d art
[PDF] quel est le secret du petit prince
[PDF] mots difficiles dans le petit prince
[PDF] mettre a profit ses connaissances
[PDF] questionnaire post campagne
[PDF] méthodologie collège 3ème
