[PDF] PHQ434 : Mécanique quantique II

View - Download PHQ434 : Mécanique quantique II

Previous PDF

Next PDF

MÉCANIQUE QUANTIQUE II

PHQ434

par

David SÉNÉCHAL

Ph.D., Professeur Titulaire

UNIVERSITÉ DESHERBROOKE

Faculté des sciences

Département de physique

30 mai 2018

2

Table des matières

Table des matières3

1 Rappels et principes de base9

A Postulats de la mécanique quantique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9

1.A.1 État d"un système. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10

1.A.2 Grandeurs physiques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10

1.A.3 Évolution temporelle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12

1.A.4 Quantification canonique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14

B Observables compatibles, ECOC. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16

1.B.1 Ensemble complet d"observables qui commutent. . . . . . . . . . . . . . . . . . .17

1.B.2 Compatibilité des mesures. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17

C Observables incompatibles et relations d"incertitude. . . . . . . . . . . . . . . . . . . . . .19

1.C.1 Incompatibilité des mesures. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19

1.C.2 Relations d"incertitude. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20

D Mouvement d"une particule. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21

1.D.1 Position. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21

1.D.2 Moment conjugué. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .22

1.D.3 Particule dans un potentiel. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .25

E Systèmes composés : produit tensoriel. . . . . . . . . . . . . . . . . . . . . . . . . . . . .26

1.E.1 Produit tensoriel d"espaces vectoriels. . . . . . . . . . . . . . . . . . . . . . . . . .27

1.E.2 Produit tensoriel d"opérateurs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .27

F Principe variationnel de Rayleigh-Ritz. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .29

2 L"oscillateur harmonique37

A États propres de l"oscillateur harmonique. . . . . . . . . . . . . . . . . . . . . . . . . . .38

2.A.1 Opérateurs d"échelle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .38

2.A.2 États propres. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .39

2.A.3 Opérateurs position et impulsion. . . . . . . . . . . . . . . . . . . . . . . . . . . .40

2.A.4 Fonctions d"onde. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .41

B Mouvement dans un champ magnétique : niveaux de Landau. . . . . . . . . . . . . . . .42

C Le champ électromagnétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .44

2.C.1 Modes électromagnétiques dans une cavité simplifiée. . . . . . . . . . . . . . .45

2.C.2 Photons. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .47

D États cohérents. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .49

2.D.1 Superposition d"états stationnaires. . . . . . . . . . . . . . . . . . . . . . . . . . . .49

2.D.2 États cohérents. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .50

3 Théorie du moment cinétique61

A Relations de commutation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .61

B Quantification du moment cinétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .63 3

4TABLE DES MATIÈRES

3.B.1 États propres du moment cinétique. . . . . . . . . . . . . . . . . . . . . . . . . .63

3.B.2 Matrices du moment cinétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .64

C Harmoniques sphériques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .67

3.C.1 Moment cinétique orbital en coordonnées sphériques. . . . . . . . . . . . . . . .67

3.C.2 Harmoniques sphériques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .69

D Moment cinétique et rotations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .74

3.D.1 Rotations en tant que transformations. . . . . . . . . . . . . . . . . . . . . . . . . .74

3.D.2 Rotations infinitésimales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .74

3.D.3 Rotations finies. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .76

3.D.4 Rotations d"une observable. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .76

3.D.5 Invariance par rotation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .77

E Niveaux de rotation des molécules. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .78

3.E.1 Le rotor quantique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .78

3.E.2 Le rigide quantique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .79

4 Systèmes à deux niveaux87

A Spin1

2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .87

4.A.1 Moment cinétique intrinsèque. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .87

4.A.2 Spineurs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .88

4.A.3 Expérience de Stern et Gerlach. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .89

B Description générale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .91

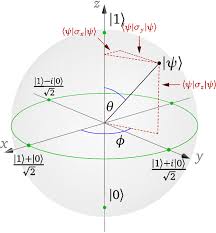
4.B.1 Sphère de Bloch. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .91

4.B.2 Correspondance avec le spin1

2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .92

4.B.3 Rotation d"un spineur. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .93

4.B.4 Observables. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .94

C Résonance magnétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .95

4.C.1 Précession de Larmor. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .95

4.C.2 Champ transverse et oscillations de Rabi. . . . . . . . . . . . . . . . . . . . . . .96

4.C.3 Résonance magnétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .97

D Autres systèmes à deux niveaux. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .102

4.D.1 Restriction aux deux niveaux les plus bas. . . . . . . . . . . . . . . . . . . . . . . .102

E Interaction lumière-matière : modèle de Jaynes-Cummings. . . . . . . . . . . . . . . . .104

5 Potentiel central et atome d"hydrogène113

A Problème à deux corps. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .113

B Mouvement d"une particule dans un potentiel central. . . . . . . . . . . . . . . . . . . . .114

5.B.1 Potentiel effectif. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .115

C Problème de Kepler : atome d"hydrogène. . . . . . . . . . . . . . . . . . . . . . . . . . .116

5.C.1 Solution de l"équation radiale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .116

5.C.2 Quantification de l"énergie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .119

5.C.3 Description des états propres. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .120

5.C.4 Raies spectrales de l"hydrogène. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .122

5.C.5 Échelles caractéristiques et atomes hydrogénoïdes. . . . . . . . . . . . . . . . . .124

D L"oscillateur harmonique tridimensionnel. . . . . . . . . . . . . . . . . . . . . . . . . . .125

6 Théorie des perturbations131

A Perturbations stationnaires. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .131

TABLE DES MATIÈRES5

6.A.1 Approximation du premier ordre. . . . . . . . . . . . . . . . . . . . . . . . . . . . .132

6.A.2 Approximation du deuxième ordre. . . . . . . . . . . . . . . . . . . . . . . . . . .133

6.A.3 Cas d"un niveau dégénéré au premier ordre. . . . . . . . . . . . . . . . . . . . . .134

B Applications. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .135

6.B.1 Effet Stark dans l"atome d"hydrogène. . . . . . . . . . . . . . . . . . . . . . . . .135

6.B.2 Force de van der Waals. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .137

C Perturbations dépendant du temps et spectres continus. . . . . . . . . . . . . . . . . . . .141

6.C.1 Série de Dyson. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .141

6.C.2 Approximation du premier ordre. . . . . . . . . . . . . . . . . . . . . . . . . . . . .142

6.C.3 Règle d"or de Fermi. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .144

6.C.4 Processus de désintégration. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .145

6.C.5 Absorption et émission stimulée de rayonnement par un atome. . . . . . . . . .147

7 Particules identiques153

A Particules indiscernables en mécanique quantique. . . . . . . . . . . . . . . . . . . . . .153

7.A.1 Rappels sur les permutations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .154

7.A.2 Opérateur de permutation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .156

7.A.3 Fermions et bosons. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .157

B Fonctions d"ondes à plusieurs fermions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .159

7.B.1 Déterminants de Slater. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .159

7.B.2 Fermions sans interactions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .160

7.B.3 Spin. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .161

7.B.4 Principe d"exclusion de Pauli. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .163

C Atomes à plusieurs électrons. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .164

7.C.1 Potentiel effectif. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .164

7.C.2 Couches électroniques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .165

7.C.3 Addition des moments cinétiques, termes spectroscopiques et règles de Hund.167

8 Mesure et environnement177

A Matrice densité. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .177

8.A.1 Motivation : système comportant deux spins. . . . . . . . . . . . . . . . . . . . . .177

8.A.2 Définition générale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .178

8.A.3 Évolution temporelle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .180

8.A.4 Trace sur un sous-système. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .181

8.A.5 Théorème de Gleason. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .182

8.A.6 Décomposition de Schmidt. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .182

8.A.7 Enchevêtrement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .184

B Le processus de mesure. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .185

8.B.1 Évolution temporelle de la matrice densité : systèmes découplés. . . . . . . .185

8.B.2 Évolution non unitaire. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .185

8.B.3 Décohérence et réduction du paquet d"ondes. . . . . . . . . . . . . . . . . . . . . .187

C Paradoxes de la réalité quantique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .189

8.C.1 Paradoxe d"Einstein-Podolsky-Rosen. . . . . . . . . . . . . . . . . . . . . . . . . . .189

8.C.2 Le paradoxe de Greenberger-Horne-Zeilinger. . . . . . . . . . . . . . . . . . . .190

8.C.3 Inégalité de Clauser-Horne-Shimony-Holt. . . . . . . . . . . . . . . . . . . . . . .192

8.C.4 Confirmations expérimentales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .195

6TABLE DES MATIÈRES

Index198

Table des problèmes

1.1 Commutateurs et anticommutateurs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30

1.2 Égalité de deux opérateurs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30

1.3 Matrice non hermitienne. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30

1.4 Mesure de l"énergie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30

1.5 Théorème de Hellmann-Feynman. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31

1.6 Sauts de particules. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31

1.7 Projecteurs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32

1.8 Bras et kets. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32

1.9 Principe d"incertitude. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .33

1.10 Particule libre. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .33

1.11 Théorème du viriel. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .33

1.12 Relation de Hausdorff. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34

1.13 Relation de Campbell-Baker-Hausdorff. . . . . . . . . . . . . . . . . . . . . . . . . . . . .35

1.14 Produits tensoriels d"opérateurs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .35

1.15 Produit tensoriel de matrices. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .35

1.16 Clônage quantique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .36

1.17 Méthode de Rayleigh-Ritz appliquée au problème de Kepler. . . . . . . . . . . . . . . .36

1.18 Méthode de Rayleigh-Ritz. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .36

2.1 Incertitude dexetpdans les états stationnaires de l"oscillateur harmonique. . . . .56

2.2 Deux oscillateurs harmoniques couplés. . . . . . . . . . . . . . . . . . . . . . . . . . . . .56

2.3 Oscillateur dans un champ électrique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .56

2.4 Oscillateur harmonique renormalisé. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .57

2.5 Relation de fermeture pour les états cohérents. . . . . . . . . . . . . . . . . . . . . . . . .57

2.6 États cohérents : éléments de matrice de la position. . . . . . . . . . . . . . . . . . . . . .57

2.7 Valeur moyenne de l"exponentielle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .58

2.8 Oscillateur forcé. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .58

2.9 États comprimés. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .58

3.1 Somme de moments cinétiques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .83

3.2 Incertitude sur Jx. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .83

3.3 Harmoniques sphériques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .83

3.4 Harmoniques sphériques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .83

3.5 Interaction d"échange. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .84

3.6 Invariance du produit scalaire. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .84

3.7 Rotation des états propres du moment cinétique. . . . . . . . . . . . . . . . . . . . . . . .84

3.8 Petite rotation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .84

3.9 Matrice de rotation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .85

3.10 Moment cinétique et axes liés à un objet. . . . . . . . . . . . . . . . . . . . . . . . . . . .85

3.11 Molécule diatomique polaire. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .85

4.1 Interaction d"échange. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .107

4.2 Expérience de Stern et Gerlach. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .108

7

Table des matières

4.3 Oscillateur fermionique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .108

4.4 Précession de Larmor. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .109

4.5 Valeurs propres d"une matrice hermitienne 22. . . . . . . . . . . . . . . . . . . . . . . .109

4.6 Renversement d"un spin. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .109

4.7 Système à deux niveaux. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .109

4.8 Écho de spin. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .110

4.9 Modèle de Jaynes-Cummings. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .110

5.1 Perturbation en 1=r2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .127

5.2 Distance la plus probable entre proton et électron. . . . . . . . . . . . . . . . . . . . . . .127

5.3 Mouvement dans une combinaison d"états stationnaires. . . . . . . . . . . . . . . . . . .127

5.4 Atome muonique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .128

5.5 Mouvement sur un cylindre. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .128

5.6 Coquilles concentriques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .128

5.7 Puits sphérique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .129

6.1 Oscillateur anharmonique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .149

6.2 Force entre un atome et une paroi conductrice. . . . . . . . . . . . . . . . . . . . . . . . .149

6.3 Oscillateur harmonique couplé à un système à deux niveaux. . . . . . . . . . . . . . . .149

6.4 Modèle de Jaynes-Cummings. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .150

6.5 Émission stimulée. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .150

6.6 Impulsion sur un oscillateur. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .150

7.1 Exercices sur les permutations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .174

7.2 Relation de fermeture à deux fermions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .174

7.3 État à trois fermions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .174

7.4 Coprobabilité. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .174

7.5 Répulsion coulombienne entre deux particules. . . . . . . . . . . . . . . . . . . . . . . .175

7.6 Terme d"échange. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .175

7.7 Terme spectroscopique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .176

8.1 Matrice densité. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .196

8.2 Enchevêtrement de spins. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .196

8.3 Paradoxe de Zénon quantique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .196

8.4 Appareil de mesure. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .196

8

CHAPITRE1

Rappels et principes de base

Le coursMécanique quantique II(PHQ430) est le deuxième de l"axe " mécanique quantique » au

baccalauréat en physique de l"Université de Sherbrooke. Le premier cours de la série,Mécanique

quantique I(PHQ330), couvre les éléments suivants :

1.Description des phénomènes quantiques qui ont suscité le développement de la théorie au début

du XXesiècle : aspects ondulatoires de la propagation des particules, aspects corpusculaires de l"interaction du rayonnement avec la matière, manifestations de la quantification de l"énergie dans les atomes, etc.

2.Description de la première théorie quantique (Bohr-Sommerfeld).

3.Mécanique ondulatoire, basée sur le concept de fonction d"onde .

4.Formalisme mathématique de la mécanique quantique : espaces de Hilbert, opérateurs, notation

de Dirac.

5.Postulats formels de la mécanique quantique.

6.Problèmes unidimensionnels : puits et barrières de potentiel, oscillateur harmonique.

7.Processus de mesure et probabilités

Le deuxième cours, l"objet de ces notes, se veut une continuité du premier. Il met plus à profit le

formalisme mathématique de la MQ en fonction d"opérateurs, traite de problèmes tridimensionnels,

introduit des méthodes d"approximation et traite de l"identité des particules.

APostulats de la mécanique quantique

Il n"y a pas de manière unique d"énoncer les postulats de la mécanique quantique, ni même de les

dénombrer. Les postulats qui suivent sont formulés légèrement différemment de ce qui a été énoncé

en PHQ330, mais le contenu est strictement équivalent. 9

Chapitre 1. Rappels et principes de base

1.A.1État d"un système

Postulat 1 : Principe de superposition

À chaque système physique est associé un espace projectif de HilbertE. L"état du système est

défini à chaque instanttpar un vecteurj (t)ideE. Tout vecteur qui diffère dej (t)ipar un

facteur multiplicatif2Creprésente le même état physique et est considéré équivalent.

1.Ce principe tire son nom du fait qu"une combinaison linéairej 1i+j 2ide deux vecteurs repré-

sente aussi un état possible du système. Cette propriété du monde quantique est primordiale.

2.Des vecteursj iet 0iqui sont des multiples l"un de l"autre (j i= 0i) étant considérés

équivalents, l"espace de HilbertEcomporte desclasses d"équivalences(des ensembles de

vecteurs équivalents) qui sont appeléesrayons. Un état physique correspond en fait à un rayon.

3.En pratique, on a l"habitude de considérer uniquement des états normés, tels queh j i=1.

Mais cette condition de normalisation ne suffit pas à spécifier de manière unique un état, car il

reste une liberté de phase, qui fait que les deux vecteurs normésj ieteij ireprésentent le même état.

4.Tout espace vectoriel est défini sur un corps K. En particulier, l"espaceEest défini sur le corps

des complexesC. Il existe des systèmes pour lesquels une définition sur les réelsRest suffisante,

mais cela est l"exception.

5.Le fait queEsoit un espace de Hilbert a un sens précis en mathématiques, relié à la convergence

du développement d"un état sur une basefjnigdans le cas d"un espace de dimension infinie. Cette exigence se traduit formellement par la libre utilisation de la relation de fermeture X n jnihnj=I(1.1) que nous allons utiliser régulièrement sans la remettre en question.

1.A.2Grandeurs physiques

Postulat 2 : Grandeurs physiques

a)À toute grandeur physique mesurableAcorrespond un opérateur linéaire hermitienAagissant

sur l"espace des étatsE. Cet opérateur est appelé l"observableassociée à la grandeur physique

A. b)Les seules valeurs possibles résultant d"une mesure deAsont des valeurs propresande l"opérateur A (icinsert d"étiquette pour les différentes valeurs propres). 10

A. Postulats de la mécanique quantique

Postulat 3 : Processus de mesure

a)SoitP(an)l"opérateur de projection vers le sous-espace deEassocié à la valeur proprean(ce sous-espace peut être de dimension 1 ou plus). Si le système est dans l"étatj i, alors une mesure deAeffectuée dans cet état donnera la valeuranavec une probabilité

P(an) =jP(an)j ij2=h jP(an)j i(1.2)

b)Le processus de mesure change l"état du système : immédiatement après, le système est dans

l"état P(an)j iou, après normalisation,

P(an)j iph jP(an)j i(1.3)

Remarques :

FLe fait que l"opérateur A soit hermitien assure que ses valeurs propres sont réelles. FRappelons qu"un projecteur P est un opérateur hermitien tel que P2=P. FSijiest un vecteur normalisé quelconque, le projecteur sur le sous-espace engendré par ce vecteur s"exprime ainsi :P=jihj. En effet, l"application dePsur un étatj idonne alors (hj i)ji, ce qui représente bien la projection du vecteurj idans la direction du vecteur ji.

FL"observable peut être représentée en fonction des projecteurs sur ses différents espaces propres

de la manière suivante : A= X n a(n)P(an)(1.4) L"ensemble des valeurs propres deAforment sontspectre, et la décomposition ci-dessus en fonction des projecteurs porte le nom dereprésentation spectralede A.

FSupposons en général qu"une valeur propreandeAsoit associée àdnvecteurs propres linéai-

rement indépendants, qu"on noteraj ri(r=1,2,...,dn). On peut toujours choisir cesdn vecteurs propres comme étant orthonormés. Dans ce cas, le projecteur P(an)s"exprime ainsi

P(an) =

dnX r=1 j rih rj(1.5) et l"observable A elle-même peut s"exprimer comme suit : A= X n dnX r=1 anj rih rj(1.6) Il n"est pas toujours pratique de tenir compte de la dégénérescence des valeurs propres de manière explicite, comme ci-dessus. On pourrait également écrire la formule générale A= X n anjanihanj(1.7)

oùjanidésigne un vecteur propre normalisé associé à la valeur proprean. Seulement, dans

cette version, on ne suppose pas nécessairement que toutes les valeurs propres sont distinctes (il y a possibilité de dégénérescence). 11

Chapitre 1. Rappels et principes de base

FL"étatj inous donne une distribution de probabilités pour la valeur d"une observableA. La valeur moyenne associée à cette distribution est hAi= X n anP(an) = X n anh jP(an)j i= X n anh janihanj i =h j X n anjanihanj j i=h jAj i (1.8) FLa variance2(A)d"une observable se calcule de manière semblable :

2(A) =hA2ihAi2=h jA2j ih jAj i2(1.9)

FLa mécanique quantique prédit une distribution de probabilité pour les valeurs mesurées d"une

observableAdans un étatj i. Pour confirmer ou infirmer cette prédiction, il est donc nécessaire

de procéder à un très grand nombre de mesures et de comparer des statistiques de mesure

avec la distribution de probabilité en question. Autrement dit, les prédictions sont statistiques,

et donc leurs vérifications sont statistiques également. Ces différentes mesures doivent être

accomplies sur le même état physiquej i. Il est donc nécessaire de préparer système dans le

même état avant la mesure, sinon les prédictions n"ont plus de sens. FComment prépare-t-on un état quantiquej ien prévision d"une mesure? Tout simplement en effectuant une ou plusieurs mesurespréparatoires: le postulat 3b nous indique qu"une mesure

va transformer un état quelconque en un état propre de l"observable mesurée. Cependant, il faut

s"assurer que cet état est unique, d"où l"importance des ECOC (voir p.17) : il faut en principe

mesurer autant d"observables qu"il est nécessaire pour spécifier de manière unique l"état après

ces mesures préparatoires, et filtrer les résultats, c"est-à-dire n"effectuer la mesure principale

(l"objet de la distribution de probabilités qu"on veut confirmer) que dans les cas où les mesures

préparatoires ont produit l"état vouluj i.

FLa projection de l"étatj isur l"espace propre associé à la valeur propre obtenue lors de la

mesure de l"observable constitue une évolution subite de l"état, appeléeréduction du paquet

d"ondes. Cette évolution subite n"obéit pas, en apparence, à l"équation de Schrôdinger. En fait,

d"un système complexe, comportant le système étudié, en plus de l"appareil de mesure et de son

environnement. C"est lorsqu"on restreint notre vision au système étudié que l"évolution semble

subite et non unitaire.

1.A.3Évolution temporelle

L"énergie totale d"un système est représentée par une observableHappeléhamiltonien. Cet

opérateur génère l"évolution dans le temps du système, telle que représentée par l"équation de

i~h@ @tj (t)i=Hj (t)i(1.10) 12

A. Postulats de la mécanique quantique

Remarques :

FEn prenant le conjugué hermitien de cette équation, on trouve i~h@ @th (t)j=h (t)jH (1.11) où il est implicite que l"opérateur hermitien H agit vers la gauche. FUne observableApeut dépendre explicitement du temps. Par exemple, l"énergie peut dépendre explicitement du temps si un champ magnétique ou électrique externe variable est appliqué. Dans ce cas, la valeur moyennehA(t)ide cette observable évolue dans le temps en raison non seulement de cette dépendance explicite, mais aussi en raison de la dépendance temporelle du vecteur d"étatj idans lequel elle est calculée : dhAi dt= @th j

Aj i+h jA

@tj i +h j@A @tj i =1 i~hh jHAj i+1 i~hh jAHj i+h j@A @tj i =1 i~hh[A,H]i+ @A @t (1.12) Cette dernière égalité porte le nom dethéorème d"Ehrenfest.

FLa solution formelle à l"équation (1.10), dans le cas où H est indépendant du temps, est

j (t)i=U(t)j (0)ioù U(t) =eitH=~h(1.13) En effet, la dérivée de l"exponentielle fait descendre un facteuriH=~h: @tU(t) =1 i~hHU(t)et donc@ @tU(t)j (0)i=1 i~hHU(t)j (0)i=1 i~hHj (t)i(1.14)

l"opérateurUest appeléopérateur d"évolutionet est unitaire :U1(t) =U†(t). L"inverse de

l"opérateur d"évolution s"obtient en changeant le signe du temps :U1(t) =U(t). Notez que cette forme de l"opérateur d"évolution ne vaut plus si le Hamiltonien dépend du temps. Dans ce cas, le premier réflexe serait de remplacerHtpar une intégrale :Rt

0dt0H(t0). Cependant,

ce réflexe ne serait le bon que si les hamiltoniens associés à des temps différents commutent

entre eux :H(t),H(t0)=0. Dans le cas contraire, il faut introduire la notion de produit chronologique, ce qui dépasse la portée de ce cours.

FLe fait que l"opérateurU(t)soit unitaire est important : cela signifie entre autres que le produit

hermitien de deux vecteurs d"état - et donc la norme d"un vecteur - est préservée par l"évolution

temporelle : h 0(t)j (t)i=hU(t) 0(0)jU(t) (0)i=h 0(0)jU†(t)U(t)j (0)i=h 0(0)j (0)i(1.15)

Par contre, les éléments de matrice d"un opérateurAne sont pas préservés, à moins que cet

opérateur commute avec H : h 0(t)jAj (t)i=h 0(0)jU†(t)AU(t)j (0)i 6=h 0(0)jAj (0)isauf si[H,A] =0 (1.16) 13

Chapitre 1. Rappels et principes de base

suppose que les états sont constants dans le temps, mais que les observables évoluent à leur place.

Les deux schémas sont équivalents, c"est-à-dire mènent aux mêmes éléments de matriceh 0jAj i

suivante en fonction du temps : h 0jAj i ! h 0(t)jAj (t)i=h 0(0)jU†(t)AU(t)j (0)i(1.17)

Selon le schéma de Heisenberg, c"est l"observableAqui évolue en fonction du temps, de la manière

suivante : A(0)!A(t) =U†(t)A(0)U(t) =eiHt=~hA(0)eiHt=~h(1.18)

On peut exprimer cette relation sous forme différentielle, en prenant la dérivée par rapport au temps :

dA dt=1 i~hHeiHt=~hA(0)eiHt=~h+1 i~heiHt=~hA(0)eiHt=~hH=1 i~h[A(t),H](1.19)

L"avantage de la formulation différentielle est qu"elle demeure valable même si le hamiltonien dépend

du temps. On peut également supposer que l"observable A dépend explicitement du temps, de sorte

quotesdbs_dbs28.pdfusesText_34

[PDF] l'analyse des textes littéraires une méthodologie complète

[PDF] technique collage artistique

[PDF] activité collage maternelle

[PDF] tableau avec collage papier

[PDF] dessin collage papier

[PDF] rituels classe anglais collège

[PDF] collage artistique journaux

[PDF] activité collage 2 ans

[PDF] rituel météo anglais

[PDF] activité collage en creche

[PDF] technique du collage en art plastique

[PDF] méthode de collecte de données quantitatives

[PDF] devoirs ? la maison au collège

[PDF] outils de collecte de données

[PDF] les devoirs ? la maison pour ou contre