[PDF] Mécanique quantique II PHQ-430

View - Download Mécanique quantique II PHQ-430

Previous PDF

Next PDF

Mecanique quantique II

PHQ-430Alexandre Blais

Departement de Physique

Universite de Sherbrooke

Fevrier 2014

2

Table des matieres

Table des matieres 1

1 Notation de Dirac 7

1.1 Rappel sur les fonctions d'ondes . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

1.2 Espace des etats : notation de Dirac . . . . . . . . . . . . . . . . . . . . . . . . . . .

9

1.2.1 Introduction des kets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9

1.2.2 Produit scalaire et introduction de l'espace dual . . . . . . . . . . . . . . . .

10

1.3 Operateurs dans l'espace de Hilbert . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11

1.3.1 Operateur adjoint . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

13

1.3.2 Operateur hermitique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

14

1.3.3 Algebre des commutateurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

15

1.3.4 Fonction d'un operateur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

15

1.3.5 Derivation d'un operateur . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

17

1.3.6 Operateurs inverses et operateurs unitaires . . . . . . . . . . . . . . . . . . .

18

1.4 Representations dans l'espace des etats . . . . . . . . . . . . . . . . . . . . . . . . . .

19

1.4.1 Relations caracteristiques d'une base orthonormee : cas discret . . . . . . . .

19

1.4.2 Relations caracteristiques d'une base orthonormee : cas continu . . . . . . . .

20

1.4.3 Representation des kets et des bras . . . . . . . . . . . . . . . . . . . . . . . .

21

1.4.4 Representation des operateurs . . . . . . . . . . . . . . . . . . . . . . . . . . .

22

1.4.5 Changement de representation . . . . . . . . . . . . . . . . . . . . . . . . . .

24

1.4.6 Trace d'un operateur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

26

1.5 Information quantique I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

26
1.6 Equations aux valeurs propres et observables . . . . . . . . . . . . . . . . . . . . . .29

1.6.1 Valeurs et etats propres d'un operateur . . . . . . . . . . . . . . . . . . . . .

29

1.6.2 Observables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

34

1.6.3 Ensembles d'observables qui commutent . . . . . . . . . . . . . . . . . . . . .

35

1.7 Representations et operateurs R et P . . . . . . . . . . . . . . . . . . . . . . . . . . .

38

1.7.1 Representation de position . . . . . . . . . . . . . . . . . . . . . . . . . . . .

39

1.7.2 Representation d'impulsion . . . . . . . . . . . . . . . . . . . . . . . . . . . .

40

1.7.3 Relation entre les representations de position et d'impulsion . . . . . . . . . .

40

4 TABLE DES MATI

ERES1.7.4 Operateurs R et P . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .41

1.8 Produit tensoriel d'espaces d'etats . . . . . . . . . . . . . . . . . . . . . . . . . . . .

42

1.8.1 Denition et proprietes du produit tensoriel . . . . . . . . . . . . . . . . . . .

43
1.8.2 Etats deE. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .44

1.8.3 Produit tensoriel d'operateurs . . . . . . . . . . . . . . . . . . . . . . . . . . .

44

1.8.4 Notations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

45

1.9 Information quantique II . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

47

1.9.1 Impossibilite de copier l'information quantique . . . . . . . . . . . . . . . . .

47

1.9.2 Registre de qubits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

47

1.9.3 Operations logiques quantiques et circuits quantiques . . . . . . . . . . . . .

48

1.10 Problemes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

50

2 Postulats de la mecanique quantique 53

2.1 Enonce des postulats . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .53

2.1.1 Description de l'etat d'un systeme . . . . . . . . . . . . . . . . . . . . . . . .

54

2.1.2 Description des grandeurs physiques . . . . . . . . . . . . . . . . . . . . . . .

54

2.1.3 Mesure des grandeurs physiques . . . . . . . . . . . . . . . . . . . . . . . . .

54

2.1.4 Resultat de mesure des grandeurs physiques . . . . . . . . . . . . . . . . . . .

54

2.1.5 Reduction du paquet d'ondes . . . . . . . . . . . . . . . . . . . . . . . . . . .

55
2.1.6 Evolution dans le temps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .56

2.1.7 Regles de quantication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

56

2.2 Mesures en mecanique quantique . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

57

2.2.1 Valeur moyenne d'un ensemble de mesures . . . . . . . . . . . . . . . . . . . .

57
2.2.2 Ecarts types et relations d'incertitude . . . . . . . . . . . . . . . . . . . . . .58

2.2.3 Compatibilite des observables et preparation d'un etat . . . . . . . . . . . . .

60

2.2.4 Mesure d'un sous-espace et enchev^etrement . . . . . . . . . . . . . . . . . . .

63

2.2.5 Application aux cas continus . . . . . . . . . . . . . . . . . . . . . . . . . . .

64
2.3 Evolution temporelle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .66

2.3.1 Conservation de la norme . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

66

2.3.2 Theoreme d'Ehrenfest . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

67
2.3.3 Evolution d'un systeme conservatif . . . . . . . . . . . . . . . . . . . . . . . .69

2.3.4 Frequences de Bohr et regles de selection . . . . . . . . . . . . . . . . . . . .

71

2.3.5 Relation d'incertitude temps-energie . . . . . . . . . . . . . . . . . . . . . . .

71

2.4 Niveaux instables et temps de vie . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

74

2.5 Problemes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

75

3 Systemes a deux niveaux 79

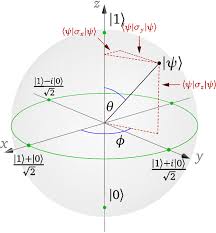
3.1 Espace de Hilbert a deux dimensions et sphere de Bloch . . . . . . . . . . . . . . . .

79

3.2 Exemples de systemes a deux niveaux . . . . . . . . . . . . . . . . . . . . . . . . . .

81

TABLE DES MATI

ERES 53.2.1 Polarisation d'un photon (?) . . . . . . . . . . . . . . . . . . . . . . . . . . .82

3.2.2 Experience de Stern et Gerlach et Spin 1=2 . . . . . . . . . . . . . . . . . . .83

3.2.3 Restriction a un systeme a deux niveaux et spin 1/2 eectif . . . . . . . . . .

86

3.3 Spin 1/2 et precession de Larmor . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

88

3.4 Spin 1/2 dans un champ transverse . . . . . . . . . . . . . . . . . . . . . . . . . . . .

89

3.4.1 Champ transverse faible . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

91

3.4.2 Champ transverse intense . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

91

3.5 Oscillations de Rabi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

91

3.6 Problemes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

94

4 Oscillateur harmonique 97

4.1 Importance de l'oscillateur harmonique en physique . . . . . . . . . . . . . . . . . . .

97

4.1.1 Loi de Hooke et approximation harmonique . . . . . . . . . . . . . . . . . . .

97

4.1.2 Champ electromagnetique . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

98

4.2 Oscillateur harmonique quantique a une dimension . . . . . . . . . . . . . . . . . . .

100

4.2.1 Operateurs de creation et d'annihilation . . . . . . . . . . . . . . . . . . . . .

101
4.2.2 Energies propres et action des operateurs d'echelle . . . . . . . . . . . . . . .102

4.2.3 Representation matricielle des operateurs d'echelle . . . . . . . . . . . . . . .

105

4.2.4 Representation des etats propres dans l'espace des positions . . . . . . . . . .

106

4.2.5 Valeurs moyennes et ecarts quadratiques moyens . . . . . . . . . . . . . . . .

108

4.3 Oscillateurs harmoniques isotropes a trois dimensions . . . . . . . . . . . . . . . . .

109

4.4 Interaction lumiere-matiere : modele Jaynes-Cummings . . . . . . . . . . . . . . . .

110
4.4.1 Etats et energies propres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .114

4.5 Problemes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

116

5 Moment cinetique en mecanique quantique 119

5.1 Passage au cas quantique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

119

5.1.1 Moments cinetiques orbitaux . . . . . . . . . . . . . . . . . . . . . . . . . . .

119

5.1.2 Relations de commutation . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

120

5.2 Moments cinetiques et rotations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

120

5.2.1 Denition de l'operateur rotation . . . . . . . . . . . . . . . . . . . . . . . . .

120

5.2.2 Rotations innitesimales et moment cinetique . . . . . . . . . . . . . . . . . .

121

5.2.3 Invariance sous rotation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

122

5.2.4 Generalisation au spin intrinseque . . . . . . . . . . . . . . . . . . . . . . . .

123

5.3 Theorie generale du moment cinetique . . . . . . . . . . . . . . . . . . . . . . . . . .

124

5.3.1 Les operateursJ+etJ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .125

5.3.2 Valeurs propres deJ2etJz. . . . . . . . . . . . . . . . . . . . . . . . . . . .126

5.3.3 Action deJsur les etatsjj;mi. . . . . . . . . . . . . . . . . . . . . . . . .129

5.3.4 Mesures deJxetJy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .129

6 TABLE DES MATI

ERES5.3.5 Representations standardsjk;j;mi(?) . . . . . . . . . . . . . . . . . . . . . .130

5.3.6 Representation matricielle du moment cinetique . . . . . . . . . . . . . . . . .

131

5.4 Application au moment cinetique orbital . . . . . . . . . . . . . . . . . . . . . . . . .

133

5.4.1 Valeurs et fonctions propres deL2etLz. . . . . . . . . . . . . . . . . . . . .133

5.4.2 Base standard de l'espace des fonctions d'onde (?) . . . . . . . . . . . . . . .138

5.4.3 Mesures et previsions physiques concernantL2etLz(?) . . . . . . . . . . . .139

5.5 Problemes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

142

6 L'atome d'hydrogene 143

6.1 Systemes a deux corps : mouvement relatif . . . . . . . . . . . . . . . . . . . . . . . .

143

6.2 Mouvement dans un potentiel central . . . . . . . . . . . . . . . . . . . . . . . . . . .

145

6.3 Atome d'hydrogene . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

146
6.3.1 Equation radiale reduite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .147

6.3.2 Solution asymptotique et quantication des energies . . . . . . . . . . . . . .

151
6.3.3 Etats propres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .152

6.4 Problemes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

155

A Theorie quantique de la mesure 157

Chapitre 1

Notation de Dirac

1.1 Rappel sur les fonctions d'ondesEn mecanique quantique, la fonction d'onde (r;t) represente notre connaissance de l'etat du

systeme. La mecanique quantique a une interpretation probabiliste : j (r;t)j2d3r(1.1) est donc la probabilite que la particule soit trouvee dans le volumed3rautour du pointrau temps t. Il s'agit de la regle de Born. On en deduit que la fonction d'onde est normee : Z j (r;t)j2d3r= 1:(1.2) En mecanique quantique, on s'interesse donc a l'espaceL2des fonctions de carres sommables

(i.e. celles pour lesquelles l'integrale ci-haut converge). Cet espace est toutefois trop general. On

ne s'interesse en fait qu'aux fonctions physiquement acceptables : partout denies, continues, indeniment derivables et bornees dans l'espace. On nommeFce sous-espace deL2.

Exemple 1.1.1

(Corail quantique).La gure 1.1 presente une structure connue sous le nom decorail quantique. Cette structure est realisee en manipulant, un a un a l'aide de la pointe d'un microscope a eet tunnel, des atomes de fer sur une surface de cuivre. L'image est prise a l'aide du m^eme microscope. L'intensite est donc fonction de la densite electronique, c'est a dire dej (r;t)j2d3r. On voit dans l'image au bas a droite, lorsque le cercle est complet, des ondes

electroniques stationnaires a l'interieur du cercle. Il est donc possible de \voir" le module carre de

la fonction d'onde directement avec cette technique experimentale. Le sous-espaceFdeL2forme un espace vectoriel. Par exemple, soit (r) et(r) dansF, on a evidemment que

8Notation de DiracFigure1.1: Creation d'un corail quantique. Atomes de fer sur une surface de cuivre. Image tiree de la page

web de IBM-Almaden :http://www.almaden.ibm.com/vis/stm/corral.html. |1 (r) +2(r) =2(r) +1 (r)2 Faveciun nombre complexe. |[ (r) +(r)] = (r) +(r)

Il existe un (r) tel que(r) + (r) = (r);(r) = 0.

Ces expressions font partie des proprietes qui doivent ^etre respectees par les elements d'un espace

vectoriel. On verie facilement que les autres proprietes devant ^etre respectees par un espace vectoriel

le sont aussi. De plus,Fest muni d'un produit scalaire (; ) =Z d

3r(r) (r)2C(1.3)

qui est tel que (; ) = ( ;):(1.4) Les fonctions d'onde (r;t) peuvent donc ^etre vues comme des vecteurs deF. L'algebre lineaire est donc le langage mathematique pertinent a la description de a la mecanique quantique.

Remarque 1.1.1.

Il est interessant de mentionner que Born a initialement suggere que la norme j j, et non la norme carree,j j2ait une interpretation de probabilite. Ce n'est que dans une note de bas de page dans son article sur le sujet qu'il mentionne que, apres m^ure re exion, il en arrive a la conclusion que l'on doit plut^ot considerer la norme au carre. Un prix Nobel pour une note de bas de page...

Remarque 1.1.2.

Lecture suggeree :x1.A du livre de Cohen-Tannoudji et al. [1]. Ceci ne sera pas presente en classe.

1.2 Espace des etats : notation de Dirac 9

1.2 Espace des etats : notation de Dirac

1.2.1 Introduction des ketsLa description de l'etat d'une particule par sa fonction d'onde (r;t) n'est pas unique. En eet, sa

transformee de Fourier (p;t) =1p2~Z 1 1 d3r (r;t)eipr=~;(1.5) est une description equivalente. Il existe en fait une innite d'autres descriptions equivalentes. La

situation est similaire a la geometrie ou une innite de systemes de coordonnees peuvent ^etre utilises

pour representer un m^eme point. Ici, on a une innite de base sur lesquelles on peut representer la fonction d'onde, et la des ondes planes exp(ipr=~) n'en est qu'un exemple. On aimerait s'aranchir de cette dependance et avoir une description independante de toutes coordonnees. De plus, on aimerait avoir un formalisme pouvant decrire l'etat de systemes quantiques n'ayant aucun equivalent classique. Le spin de l'electron est un exemple. On ne peut en eet decrire l'etat du spin d'un electron en utilisant une fonction d'onde (r;t) dependant seulement de la positionret du tempst.

La notion de vecteur en algebre lineaire est utile car elle permet de decrire un systeme sans reference

particuliere a un systeme de coordonnees. On peut en eet faire de l'algebre lineaire de facon completement symbolique sans specier immediatement de base pour les vecteurs et les operateurs agissants sur ceux-ci.

C'est l'idee de Dirac que d'utiliser un espace vectoriel pour representer l'etat d'un systeme quantique.

On dira donc que l'etat d'un systeme quantique est un vecteur d'etat j (t)i(1.6)

qui est element de l'espace de HilbertE, aussi appeleespace des etats. On appellera ce vecteur d'etat

unket. Pour tout ket on utilisera la notation : j i:(1.7) A toute fonction d'onde (r;t)on associe donc un vecteur d'etatj (t)i. La dependance spatialer n'appara^t plus dans le ket. Nous verrons en eet plus loin que (r;t) correspond aux composantes du ketj (t)idans la baser. De m^eme, (p;t) n'est qu'une composante dej (t)idans la basep. Donc, contrairement a la representation du cours precedent de mecanique quantique ou une innite de fonctions d'ondes dierentes peuvent representer un m^eme systeme, on aura ici un ket unique representant ce m^eme etat physique. Un espace d'HilbertEest un espace vectoriel muni d'un produit scalaire hermitien deni positif. On demande aussi queEsoitcomplet: c'est-a-dire que la sequence de Cauchy de tout element deE converge vers un element deE. Cette derniere consideration plus mathematique ne sera pas bien importante pour ce cours.

10Notation de Dirac1.2.2 Produit scalaire et introduction de l'espace dual

Le produit scalaire de deux ketsj ietjiest

(j i;ji)2C:(1.8) Dirac a propose d'introduire la notation suivante pour le produit scalaire :

(j i;ji) =h ji:(1.9)En anglais, on nomme le symboleh j iunbracket. Suivant toujours la notation suggeree par Dirac,

on introduit le bra : h j:(1.10) Puisque l'existence du produit scalaire est l'une des caracteristiques de l'espace de Hilbert, on en deduit qu'a tout ket correspond un bra (sinon, ce ket n'est pas element deE). Toutefois, a tout bra ne correspond pas necessairement un ket. Cette diculte technique intervenant dans un espace de dimension innie ne nous g^enera jamais en pratique. Nous reviendrons sur cela a la sectionx1.4.2. Plus de details a ce sujet se trouvent aussi a la sectionx1.B.c.du premier volume du livre de

Cohen-Tannoudjiet al.[1].

De facon technique nous dirons que le brah jest element deE, l'espacedualaE. L'exemple suivant clariera cette notion nalement tres simple. Considerons un espace de Hilbert de dimension nien. Choisissons une base telle que l'on puisse representer les ketsj ietjipar j i:=0 B BBBB@ 1 2... n1 C

CCCCA;ji:=0

B BBBB@ 1 2... n1 C

CCCCA;(1.11)

ou les ietisont des nombres complexes. (Le symbole := signie \represente" plut^ot que l'egalite.) Comme a l'Eq. (1.3), le produit scalaire de ces deux vecteurs est deni par h ji=nX i=1 ii;(1.12) c'est-a-dire le produit du complexe conjugue du vecteur ligne avec le vecteur colonne : h ji=

1; 2;:::; n

0 B BBBB@ 1 2... n1 C

CCCCA:(1.13)

1.3 Operateurs dans l'espace de Hilbert 11Le brah j, element dual dej i, est donc simplement (dans une base donnee) le transpose complexe

conjugue du vecteur colonne : h j:=

1; 2;:::; n

:(1.14) On peut aussi imaginer un espace de dimension innie ou les composantes des kets sont donnees par un indice continu. Dans ce cas, le produit scalaire devient simplement h ji=Z dr

3 (r)(r);(1.15)

un resultat familier du premier cours de mecanique quantique et deja donne a l'

Eq. (1.3).

De la discussion precedente, on en deduit que la correspondance entre bra et ket est antilineaire :

1j 1i+2j 2i !1h 1j+2h 2j:(1.16)

Resumons ici les proprietes importantes du produit scalaire, en utilisant la notation de Dirac : h ji=hj i(1.17) h j[1j1i+2j2i] =1h j1i+2h j2i(1.18) h j ireel et positif:(1.19)

On dira qu'un ket estnormesi

h j i= 1:(1.20)

On dira que deux kets sontorthogonauxsi

h ji= 0:(1.21)

Finalement deux kets sontorthonormauxsi

h j i= 1 ethji= 1 eth ji= 0:(1.22)

1.3 Operateurs dans l'espace de Hilbert

Un operateur transforme un ket deEen un autre ket deEet un bra deEen un autre bra deE.

Par exemple

j 0i=Aj i h0j=hjB:(1.23)

Un operateurlineaireest tel que

A[1j 1i+2j 2i] =1Aj 1i+2Aj 2i:(1.24)

Le produit de deux operateurs n'est generalement pas commutatif :

AB6=BA:(1.25)

12Notation de DiracOn introduit donc lecommutateur

[A;B] =ABBA:(1.26) On appelleelement de matricedeAle produit scalaire dej 0i=Aj iavec un autre ketji

hj 0i=hj(Aj i) = (hjA)j i=hjAj i:(1.27)Cet element de matrice est un nombre (complexe ou reel) et il commute donc avec tout autre

operateur hjAj iB=BhjAj i:(1.28)

Exemple 1.3.1

(Operateur de projection).Considerons un ketj inorme. On denit l'operateur de projection : P =j ih j:(1.29) L'action de cet operateur sur un ket quelconque est P ji=j ih ji=h jij i:(1.30) On obtient donc d'un ket arbitrairejiun ket proportionnel aj i, avech jicomme coecient de proportionnalite. On peut donc se faire une interpretation geometrique claire de l'action de cet operateur : il projette tout ket surj i. Projeter deux fois sur le m^eme ket laisse necessairement le resultat inchange : P

2 ji= (j ih j)(j ih j)ji=j ih j ih ji=h jij i(1.31)

et on a donc que P

2 =P :(1.32)

Exemple 1.3.2

(Projecteur dans un sous-espace).Considerons lesnkets orthonormauxj 1i, j 2i,...j ni: h ij ji=ij(1.33) On designeEnle sous-espace deEsous-tendu par cet ensemble. On denit le projecteur surEn P n=nX i=1j iih ij(1.34)

1.3 Operateurs dans l'espace de Hilbert 13

On a que

P 2n= nX i=1j iih ij! 0 nX j=1j jih jj1 A nX i;j=1h ij jij iih jj nX i;j=1 ijj iih jj nX i=1j iih ij =Pn(1.35) et P nji=nX i=1j iih iji=nX i=1h ijij ii nX i=1c

ij ii:(1.36)Agissant sur un ket quelconque, cet operateur donne donc la superposition lineaire de tous les

membres deEn. Il s'agit donc bien d'un projecteur surEn.

Exemple 1.3.3

(Equation de Schrodinger).Dans la notation de Dirac, l'equation de Schrodinger prend la forme i~ddt j i=Hj i;(1.37) ou l'operateurHest Hamiltonien du systeme. De m^eme, l'equation de Schrodinger independante du temps devient

Hj i=Ej i;(1.38)

ou E est l'energie propre correspondant au ketj i. Comme il deviendra clair plus bas, cette expression

n'est rien d'autre qu'une equation aux valeurs propres.

1.3.1 Operateur adjoint

Soit le ketj 0i=Aj i.A ce ket, correspond le bra

h 0j=h jAy;(1.39) ouAyest l'adjoint hermitiquedeA. Pour un nombre complexe, l'adjoint hermitique n'est que le complexe conjugue :y=. Pour une matrice, il s'agit du transpose complexe conjugue. Cette relation est plus evidente en considerant le produit scalaire. En eet, on a que h 0ji=h jAyji(1.40) et hj 0i=hjAj i:(1.41)

14Notation de DiracOr, puisqueh 0ji=hj 0i, on en deduit donc que

h jAyji=hjAj i:(1.42) Voici quelques proprietes de la conjugaison hermitique : (A)y=Ay(1.43) (Ay)y=A(1.44) (A+B)y=Ay+By:(1.45) Mais quand est-il du produitABde deux operateurs? Considerons ji=ABj i=A(Bj i)Aji(1.46)

On a alors

hj=hjAy=h jByAy(1.47)

On en deduit donc

(AB)y=ByAy:(1.48) Exemple 1.3.4((jxihyj)y= ?).Utilisant l'expression (1.42), puis l'expression (1.17) on peut ecrire h j(jxihyj)yji=hj(jxihyj)j i =hjxihyj i =hxjih jyi =h jyihxji:(1.49)

Ceci implique que

(jxihyj)y=jyihxj:(1.50)

1.3.2 Operateur hermitique

Un operateurAest dit hermitique si

Aquotesdbs_dbs28.pdfusesText_34

[PDF] l'analyse des textes littéraires une méthodologie complète

[PDF] technique collage artistique

[PDF] activité collage maternelle

[PDF] tableau avec collage papier

[PDF] dessin collage papier

[PDF] rituels classe anglais collège

[PDF] collage artistique journaux

[PDF] activité collage 2 ans

[PDF] rituel météo anglais

[PDF] activité collage en creche

[PDF] technique du collage en art plastique

[PDF] méthode de collecte de données quantitatives

[PDF] devoirs ? la maison au collège

[PDF] outils de collecte de données

[PDF] les devoirs ? la maison pour ou contre