 Exercices de mathématiques
Exercices de mathématiques
Exercice 2 : Taux d'évolution – Suites – Ajustement affine l'énergie dissipée à l'extérieur au cours de la nuit
 Ajustement dun nuage de points
Ajustement dun nuage de points
cours du temps. Pour les. 10 premiers mois du site on dispose ... ◦ même quand les points sont presque alignés
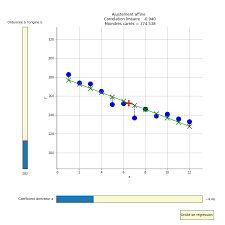 Statistiques à deux variables MathsComp 1 Ajustement affine
Statistiques à deux variables MathsComp 1 Ajustement affine
Nous étudierons dans ce cours les ajustements affines les ajustements exponentiel et parabolique pou- Corrigés d'exercices du manuel. Page 29. Question 1 ...
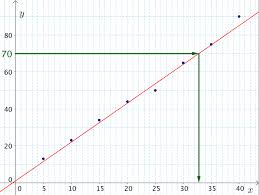 STATISTIQUES À DEUX VARIABLES
STATISTIQUES À DEUX VARIABLES
Méthode : Effectuer un ajustement se ramenant par changement de variable à un ajustement affine. Vidéo https://youtu.be/nVDL0razClY. On a relevé la population
 DEUG SV2 : MATH´EMATIQUES ET STATISTIQUES
DEUG SV2 : MATH´EMATIQUES ET STATISTIQUES
On voit que vres := vy − vaff = vy(1 − r2) est petite lorsque r2 est tr`es proche de 1. 2.1.3 Exercices sur l'ajustement affine SUJETS D'EXAMENS 2001-2003.
 Feuille dexercices Séries statistiques à deux variables 1/4 TP1
Feuille dexercices Séries statistiques à deux variables 1/4 TP1
En cours de fabrication on prélève tous les quarts d'heure un échantillon Exemples d'ajustements se ramenant à un ajustement affine (exercices d'examen).
 D.A.E.U. RÉVISIONS EN VUE DE LEXAMEN
D.A.E.U. RÉVISIONS EN VUE DE LEXAMEN
On utilisera par la suite l'ajustement affine suivant : y = −125x +826. Le cours du marché offre un prix de 530 € le kilomètre de tissu fabriqué par l ...
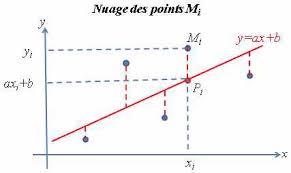 Droite des moindres carrés 1. Droite des moindres carrés (ou de
Droite des moindres carrés 1. Droite des moindres carrés (ou de
Sur ce sujet voir les exemples traités en cours et les exercices 2 à 4. Interpréter le résultat obtenu. Exercice 6. On a procédé à l'ajustement affine d'un ...
 ISCID-CO - Prépa 1 ULCO - Dunkerque STATISTIQUES ET
ISCID-CO - Prépa 1 ULCO - Dunkerque STATISTIQUES ET
Un ajustement affine est-il justifié ? 4. Déterminer une équation de la Exercice 5 Dans un cours de statistique l'enseignant présente trois thèmes
 MATHÉMATIQUES Série : Sciences et Technologies de Laboratoire
MATHÉMATIQUES Série : Sciences et Technologies de Laboratoire
18 juin 2019 Le sujet est composé de 4 exercices indépendants. Le ... Affirmation 1 : Un ajustement affine du nuage de points Mi (xi ;yi ) est adapté.
 STATISTIQUES
STATISTIQUES
d'une société au cours des 6 dernières années : Méthode : Utiliser un ajustement affine ... b) On prend (G1G2) comme droite d'ajustement.
 Exercices de mathématiques
Exercices de mathématiques
Exercice 2 : Taux d'évolution – Suites – Ajustement affine . que 285 patients ont dû subir un examen complémentaire suite à leur dernière prise de sang ...
 Statistiques à deux variables MathsComp 1 Ajustement affine
Statistiques à deux variables MathsComp 1 Ajustement affine
Nous étudierons dans ce cours les ajustements affines les ajustements Tracer le nuage de points dans le repère donné en fin d'exercice (Durée x en ...
 Feuille dexercices Séries statistiques à deux variables 1/4 TP1
Feuille dexercices Séries statistiques à deux variables 1/4 TP1
TP1 : Exemple d'ajustement affine par la méthode de Mayer En cours de fabrication on prélève tous les quarts d'heure un échantillon pour lequel on ...
 Ajustement dun nuage de points
Ajustement dun nuage de points
9 janv. 2018 Ajustement affine du nuage de points ... examen de mathématiques à partir du temps consacré à la préparation de cet examen. Pour chaque.
 Régression - Droite des moindres carrés 1. Droite des moindres
Régression - Droite des moindres carrés 1. Droite des moindres
b) Calculer le coefficient de corrélation linéaire entre x et y. Interpréter le résultat obtenu. Exercice 6. On a procédé à l'ajustement affine d'un nuage de
 Statistique à deux variables
Statistique à deux variables
Avec les données de l'exercice précédent représenter à l'aide d'un tableur le nuage de points correspondant
 Ajustement dun nuage de points
Ajustement dun nuage de points
8 janv. 2018 Ajustement affine du nuage de points ... examen de mathématiques à partir du temps consacré à la préparation de cet examen. Pour chaque.
 Première période
Première période
16 avr. 2007 Cours : chap 1 Indice et taux evolution ... Cours exemple probabilité conditionnelle ... Fin du cours ajustement affine + exercices.
 DEUG SV2 : MATH´EMATIQUES ET STATISTIQUES
DEUG SV2 : MATH´EMATIQUES ET STATISTIQUES
Ces notes sont une rédaction du cours oral en amphithéâtre. 2.1.3 Exercices sur l'ajustement affine . ... 3 Sujets d'examens 2001-2003.
DEUG SV2: MATH
´EMATIQUES ET
STATISTIQUES
M. Gradinaru
2003-2004
2Avant propos
Ces notes sont une r´edaction du cours oral en amphith´eˆatre. Il s"agit d"un document de travail et pas d"un ouvrage; il est destin´e `a la distribution aux ´etudiants de DEUG SV2, s´erie BC, de l"Universit´e de Nancy.Nancy, septembre-d´ecembre 2003 M. Gradinaru
TABLE DES MATI
`ERES3Table des mati`eres
1 Math´ematiques 1
1.1 Compl´ements d"alg`ebre lin´eaire . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.1 Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.2 Syst`emes d"´equations lin´eaires: g´en´eralit´es et deux cas particuliers . 2
1.1.3 Syst`emes depvecteurs dansRn; lien avec les syst`emes lin´eaires. . . 4
1.1.4 Retour sur les matrices: op´erations avec des matrices; lien avec les
syst`emes lin´eaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71.1.5 D´eterminants . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.1.6 Exercices d"alg`ebre lin´eaire . . . . . . . . . . . . . . . . . . . . . . . 9
1.2 Fonctions de plusieurs variables . . . . . . . . . . . . . . . . . . . . . . . . 12
1.2.1 Fonctions de deux variables . . . . . . . . . . . . . . . . . . . . . . 12
1.2.2 Fonctions de plusieurs variables . . . . . . . . . . . . . . . . . . . . 13
1.2.3 Fonctions vectorielles de plusieurs variables . . . . . . . . . . . . . . 14
1.2.4 Extr´emum d"une fonction de deux variables. . . . . . . . . . . . . . 14
1.2.5 Exercices sur les fonctions de plusieurs variables . . . . . . . . . . . 15
1.3´Equations diff´erentielles de premier ordre . . . . . . . . . . . . . . . . . . . 17
1.3.1´Equations `a variables s´eparables . . . . . . . . . . . . . . . . . . . . 17
1.3.2´Equations lin´eaires . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.3.3´Equations de Bernoulli . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3.4´Equations de Ricatti . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.3.5 Exercices sur les ´equations diff´erentielles . . . . . . . . . . . . . . . 19
2 Statistiques 21
2.1 Statistique descriptive `a deux dimensions . . . . . . . . . . . . . . . . . . . 21
2.1.1 D´efinitions et notations . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.1.2 Ajustement affine: m´ethode des moindres carr´ees . . . . . . . . . . 22
2.1.3 Exercices sur l"ajustement affine . . . . . . . . . . . . . . . . . . . . 23
2.2 Test deχ2(chi-deux) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2.1 Test deχ2de conformit´e . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2.2 Test deχ2d"homog´n´eit´e . . . . . . . . . . . . . . . . . . . . . . . . 27
2.2.3 Test deχ2d"ind´ependance . . . . . . . . . . . . . . . . . . . . . . . 28
2.2.4 Exercices sur le test deχ2. . . . . . . . . . . . . . . . . . . . . . . 29
2.3 Estimation pour l"esp´erance et la variance . . . . . . . . . . . . . . . . . . 31
4TABLE DES MATI`ERES
2.3.1 Estimation ponctuelle . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.3.2 Estimation par intervalle de confiance . . . . . . . . . . . . . . . . . 32
2.3.3 Exercices sur l"estimation . . . . . . . . . . . . . . . . . . . . . . . 36
2.4 Tests pour l"esp´erance et la variance . . . . . . . . . . . . . . . . . . . . . . 37
2.4.1 Tests de conformit´e . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
2.4.2 Test d"homog´en´eit´e pour deux ´echantillons ind´ependants . . . . . . 39
2.4.3 Test d"homog´en´eit´e de l"esp´erance pour deux ´echantillons appari´es. 41
2.4.4 Exercices pour les tests . . . . . . . . . . . . . . . . . . . . . . . . . 42
3 Sujets d"examens 2001-2003 45
1Chapitre 1
Math´ematiques
1.1 Compl´ements d"alg`ebre lin´eaire
1.1.1 Matrices
Unematriceest un tableau rectangulaire de nombres: une matricen×p A:=( (((a11a12···a1p
a a n1an2···anp) )))= (aij)1?i?n,1?j?p. Les entiersnetpsont sup´erieures ou ´egaux `a 1. Unematrice colonneest une matrice avecp= 1 et unematrice ligneest une matrice avecn= 1. Unematrice carr´eeest une matrice avecn=p. Les nombres qui constituent la matrice s"appellentcoefficientsde la matrice. Ainsiaijest le coefficient situ´e sur lai-`eme ligne et laj-`eme colonne. Les nombres consid´er´es seront
toujours des r´eels. La matrice not´eeOsera la matrice constitu´ee que des 0. La matrice carr´een×nsuivante: I n=( (((1 0···00 1···0......···...
0 0···1)
est lamatrice identit´e d"ordren. On dit aussi qu"il s"agit d"unematrice diagonale particuli`ereIn= diag(1,1,...,1). Les ´el´ements deRn=R×R...Rsont desn-uplets nomm´esvecteurs. On ´ecrit les vecteurs comme des matrices ligne mais dans les calculs alg´ebriques on les ´ecrira comme des matrices2CHAPITRE 1. MATH´EMATIQUES
colonne: ?v:=( (((v 1 v 2... v n) On peut ´ecrireun syst`eme{?u1,?u2,...,?up}depvecteurs comme une matrice obtenue en mettant ensemble lespcolonnes: ?u1?u2... ?up?=( (((u11u21···up
1u12u22···up
2......···...
u1nu2n···upn)
et on l"appellematrice du syst`eme de vecteurs.1.1.2 Syst`emes d"´equations lin´eaires: g´en´eralit´es et deux cas particuliers
a. G´en´eralit´es.La forme canonique d"un syst`eme den´equations `apinconnues est (S)? ??a11x1+a12x2+...+a1pxp=t1
a21x1+a22x2+...+a2pxp=t2
a n1x1+an2x2+...+anpxp=tn, o`u les inconnues sontx1,x2,...,xn. La forme matricielle de ce syst`eme est A (((x 1 x 2... x n) (((t 1 t 2... t n)La forme vectorielle de ce syst`eme est
x1?a1+x2?a2+...+xp?ap=?t,
o`u ?a 1=( (((a 11 a 21...a n1) ))),...,?ap=( (((a 1p a 2p... a np) )))et?t=( (((t 1 t 2... t n) b. Syst`emes2×2.La forme canonique d"un syst`eme de deux ´equations `a deux inconnues est: (S)?a1x+b1y=c1 a
2x+b2y=c2.
1.1. COMPL
´EMENTS D"ALG`EBRE LIN´EAIRE3
Ici les inconnues sontxetyetai,bi,ci,i= 1,2 sont les coefficients. Sa forme matricielle est ?a1b1 a 2b2?? x y? =?c1 c 2? La matrice du syst`eme et respectivement la matrice augment´ee sont ?a1b1 a 2b2? et?a1b1c1 a2b2c2?
R´esoudre le syst`eme (S)signifie de trouver tous les couples (x,y) desolutionsquiv´erifient `a la fois les deux ´equations de (S). On utilisera lam´ethode de Gauss: effectuer
des "op´erations" sur les lignes pour obtenir un syst`eme ´equivalent, c"est-`a-dire un syst`eme
ayant la mˆeme solution que le syst`eme initial. Les op´erations: - permutation de deux lignes - produit d"une ligne par un r´eel non nul - remplacement d"une ligne par la combinaison lin´eaire de cette ligne et une autre ligne ayant pour but de faire apparaˆıtre un 0 sur la 1`ere colonne ("triangulariser" la matrice du syst`eme)?¯a1¯b1¯c10¯b2¯c2?
En fait, apr`es op´erations on trouve
?a1b1c10a1b2-a2b1a1c2-a2c1?
et1. sia1b2-a2b1?= 0 le syst`eme a une solution unique
y=a1c2-a2c1a1b2-a2b1etx=c1b2-c2b1a
1b2-a2b1
2. sia1b2-a2b1= 0 eta1c2-a2c1?= 0, le syst`eme n"a pas de solution.
3. sia1b2-a2b1= 0 eta1c2-a2c1= 0 le syst`eme est r´eduit `aa1x+b1y=c1et il y a
une infinit´e de solutions. c.Syst`emes 3×3. La forme canonique d"un syst`eme de trois ´equations `a trois inconnues est (S)? ?a1x+b1y+c1z=d1
a2x+b2y+c2z=d2
a3x+b3y+c3z=d3.
de matrice augment´ee (a1b1c1d1
a2b2c2d2
a3b3c3d3)
4CHAPITRE 1. MATH´EMATIQUES
La m´ethode de r´esolution sera la mˆeme (la m´ethode de Gauss) avec les mˆemes op´erations
sur les lignes ayant pour but d"obtenir la matrice traingulaire suivante: (¯a1¯b1¯c1¯d10¯b2¯c2¯d2
0 0 ¯c3¯d3)
Une variante de la m´ethode de Gauss estla m´ethode du pivot. Il s"agit de faire plusieurs ´etapes dont chacune consiste `a construire le syst`emei+ 1 `a partir du syst`emeiavec les op´erations suivantes: - on choisit la ligneiet un coefficient sur cette ligneaij?= 0; on divise cette ligne par a ij; de cette fa¸con on obtient pour coefficient dexjsur cette ligne 1;- on retranche des ´equations suivantes lai-`eme ´equation multipli´ee par des r´eels qui
permettent d"obtenir 0 comme coefficients dexjdans ces ´equations; - si une ´equation est de la forme 0 = cste.avec la constante non nulle, le syst`eme n"a pas de solution; si la constante est nulle il y a une infinit´e de solutions.1.1.3 Syst`emes depvecteurs dansRn; lien avec les syst`emes
lin´eaires. Revenons `a l"´equation vectorielle dansRn, ´equivalente au syst`eme (S), x1?a1+x2?a2+...+xp?ap=?t,
o`u ?a 1=( (((a 11 a 21...a n1) ))),...,?ap=( (((a 1p a 2p... a np) )))et?t=( (((t 1 t 2... t n)
Sipour tout choix detle syst`eme a
- au plus une solution, on dit que{?a1,?a2,...,?ap}est une famillelibre; - au moins une solution, on dit que{?a1,?a2,...,?ap}est une familleg´en´eratrice; - une unique solution (sous l"hypoth`ese supplimentaire quen=p), on dit que la famille {?a1,?a2,...,?ap}est unebase. `A partir d"une matrice, en appliquant les op´erations ´el´ementaires sur les lignes, ontrouve unematrice r´eduite. On peut lire les propri´et´es de la famille de vecteurs `a partir
de la forme obtenue. On applique les op´erations ´el´emantaires `a la matrice ?a1?a2... ?ap?=( (((a11a12···a1p
a a n1an2···anp)1.1. COMPL
´EMENTS D"ALG`EBRE LIN´EAIRE5
Plusieurs cas apparaissent:
i)si le nombre de vecteurs est plus petit que la dimension de l"espace,p < n, la matrice estr´eduite de type Ilorsque: - la matrice carr´eep×pavec les premi`eresplignes est triangulaire sup´erieure `a coefficients diagonaux (pivots) non nuls; - les autresn-plignes ont que des z´eros.0?• • •
0 0?• •
0 0 0?•
0 0 0 0?
0 0 0 0 0...............
0 0 0 0 0)
Toute famille depvecteurs dansRn,p < n, ayant une matrice r´eduite de type I est une famillelibre(oulin´eairement ind´ependante). ii)si le nombre de vecteurs est plus grand que la dimension de l"espace,p > n, la matrice estr´eduite de type IIlorsque: - la matrice carr´een×navec les premi`eresncolonnes est triangulaire sup´erieure `a coefficients diagonaux (pivots) non nuls; - les autresn-pcolonnes ont des coefficients quelconques.0?• • • • ··· •
0 0?• • • ··· •
0 0 0?• • ··· •
0 0 0 0?• ··· •)
Toute famillepvecteurs dansRn,p > n, ayant une matrice r´eduite de type II est une familleg´en´eratrice. iii)si le nombre de vecteurs est ´egal `a la dimension de l"espacep=n, la matrice carr´ee estr´eduite de type IIIlorsque la matrice carr´eer×r, avecr?nest triangulaire sup´erieure `arcoefficients diagonaux (pivots) non nuls: - sir=n=p, c"est-`a-dire, si tous les coefficients diagonaux (pivots) sont non nuls la famille est unebase; - sir < n=p, c"est-`a-dire, s"il y an-rz´eros sur la diagonale, alors il y a seulementr < nvecteurs lin´eairement ind´ependants.6CHAPITRE 1. MATH´EMATIQUES
0?• • • ··· •
0 0?• • ··· •
0 0 0?• ··· •
0 0 0 0?··· •...............···...
0 0 0 0 0···?)
)))))))))ou(0?• • • ··· •
0 0?• • ··· •
0 0 0?• ··· •
0 0 0 0 0···0...............···...
0 0 0 0 0···0)
Le rang d"une matriceest la dimension de la matrice carr´ee maximale triangulaire sup´erieure ayant tous les pivots non nuls. Autrement dit, il s"agit du nombre maximal de vecteurs lin´eairement ind´ependants que l"on peut extraire de la famille. Ainsi le rang d"une matrice r´eduite de type I ou II estp, celui d"une matrice r´eduite de type II estr(donc encore une foisr=psi la famille est une base). Toute famille libre depvecteurs dansRn,p < n, peut ˆetre complet´ee parn-pvecteurs deRnde sorte que la famille denvecteurs deRnobtenu soit une base. Toute famille g´en´eratrice depvecteurs deRn,p > n, inclut au moins une sous-famille de nvecteurs qui est une base. Si on revient au syst`eme (S) et on applique un certain nombre de fois, disonsrles deuxr`egles de la m´ethode du pivot (obtenir un pivot ´egal `a 1 et ensuite faire disparaˆıtre des
´equations suivantes l"inconnue de mˆeme indice que le pivot). On suppose que lesrpremi`eres inconnues ont des coefficients pivot et que les ´equations dont tous les coefficients sont nuls x x r+αr,r+1xr+1+...+αr,pxp=τr0 =τr+1...
0 =τn
- sir=p=nalors le syst`eme admet uneunique solution; - sir=p < n - siτp+1=...=τn= 0 on supprime lesn-p´equations de la forme 0 = 0 et les p=r´equations restantes donnentsolution unique; - si au moins un desτp+1,...,τnn"est pas nul il y a une ´equation impossible, donc il n"y a pas de solution; - sir=n < pil y ap´equations qui donnentx1,...,xn=ren fonction dexn+1,...,xp, doncil y a une infinit´e de solutions;1.1. COMPL
´EMENTS D"ALG`EBRE LIN´EAIRE7
- sir < petr < n - siτr+1=...=τn= 0 on supprime lesn-r´equations de la forme 0 = 0 et il rester´equations; on obtientx1,...,xren fonction dexr+1,...,xp, doncil y a une infinit´e de solutions; - si au moins un desτr+1,...,τnn"est pas nul il y a une ´equation impossible, donc il n"y a pas de solution.1.1.4 Retour sur les matrices: op´erations avec des matrices; lien
avec les syst`emes lin´eaires Etant donn´ees deux matrices de mˆeme formatn×p,A= (aij) etB= (bij), on appelle somme deAetBla matrice de mˆeme formatA+B= (aij+bij). Etant donn´es un r´eelλet une matricen×p,A= (aij), on appelleproduit deApar le scalaireλla matrice de mˆeme format queA,λA= (λaij). L"addition des matrices est associative, commutative, admet un ´el´ement neutre, la matrice Oet toute matrice admet une oppos´ee. La multiplication des matrices par un scalaire est distributive par rapport `a l"addition des matrices, mais aussi par rapport `a l"addition des scalaires et elle est associative pour le produit des scalaires. On ne peut pas multiplier deux matrices quelconques. Il faut respecter les formats des deux facteurs. Une matriceA= (aij) de formatn×ppeut ˆetre multipli´ee `a droite seulement avec des matricesB= (bij) de formatp×q, c"est-`a-dire le nombre de colonnes de la premi`ere matrice doit ˆetre ´egal au nombre de lignes de la deuxi`eme. Leproduit deAparBest la matrice de formatn×qet de coefficients (cij), o`ucij=?p ?=1ai?b?j. Ainsi pour calculer le coefficient (i,j) de la matrice produit on fait le produit scalaire des deux vecteurs suivants: la ligneide la matriceAet la colonnejde la matriceB: (((a i1 a i2... a ip) (((b 1j b 2j... b pj) )))>=p? ?=1a i?b?j. Lorsqu"il existe le produit des matrices est associatif: siAest de formatn×p, siBest de formatp×qet siCest de formatq×ralors (AB)C=A(BC) est une matricen×r. Le produit de matrices, lorsqu"il existe, est distributif `a droite et `a gauche pour l"addition. Si on revient `a l"´ecriture matricielle des syst`emes, on voit que le membre de gauche est en fait la multiplication de la matrice des coefficientsAde formatn×pavec la matrice8CHAPITRE 1. MATH´EMATIQUES
colonneXde formatp×1 pour obtenir une matrice colonnen×1 qu"on compare `a la matricetde formatn×1.Il est clair que les matrices carr´ees peuvent ˆetre multipli´ees mais leur produit n"est pas
commutatif: en g´en´eralAB?=BAlorsque les matricesAetBsont carr´eesn×n.Toutefois pour la multiplication de matrices carr´eesn×n, il y a un ´el´ement neutre qui est
la matrice identit´eIn. En effet on peut v´erifier queAIn=InA=A. Une matriceAcarr´een×nest diteinversibles"il existe une matrice not´eeA-1carr´ee n×ntelle que:AA-1=A-1A=In.A-1s"appelle lamatrice inverse deA. Soit le syst`eme den´equations `aninconnuesAX=t. Lorsque la matriceAest inversible on peut multiplier `a gauche avecA-1pour obtenirA-1(AX) =A-1tou ´equivalent (A-1A)X=A-1tou encoreX=A-1t, car (A-1A)X=InX=X. Donc r´esoudre le syst`eme revient `a inverser la matriceA(si elle est inversible) et ensuite de calculerA-1t.On a vu que toute matrice carr´een×n,Apeut ˆetre transform´ee par une suite d"op´erations
quotesdbs_dbs45.pdfusesText_45[PDF] ajustement affine d'un nuage de points PDF Cours,Exercices ,Examens
[PDF] ajustement affine exercices corrigés PDF Cours,Exercices ,Examens
[PDF] ajustement affine nuage de points PDF Cours,Exercices ,Examens
[PDF] ajustement de la loi de gumbel PDF Cours,Exercices ,Examens
[PDF] ajustement statistique hydrologie PDF Cours,Exercices ,Examens
[PDF] ajuster équation de reaction 4ème Physique
[PDF] Ajuster la stoechiometrie d'une équation 2nde Physique
[PDF] ajuster les coefficients stoechiométriques des réactions suivantes 2nde Physique
[PDF] Ajuster une équation de réaction 4ème Physique
[PDF] Ajuter les nombres stoechiometriques 2nde Physique
[PDF] AKUKA peuple TOLAI 2nde Musique
[PDF] Al + Infinitif + Imparfait - Espagnol 3ème Espagnol
[PDF] Al Andalus devoir 2nde Espagnol
[PDF] al khwarizmi algorithme PDF Cours,Exercices ,Examens
