[PDF] Fiche technique sur les limites

Fiche technique sur les limites

5 Fonctions logarithme et exponentielle. 5.1 Fonction logarithme. Comparaison de la fonction logarithme avec la fonction puissance en +∞ et en 0. En + ∞ lim.

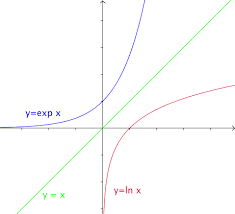FONCTION LOGARITHME NEPERIEN

Remarque : Les fonctions puissances imposent leur limite devant la fonction logarithme népérien. a) Calculer les limites de f aux bornes de son ensemble de ...

La fonction logarithme népérien

Dec 3 2014 Conclusion : la fonction ln est dérivable sur ]0; +∞[ et (ln x)′ = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...

fonctions-usuelles.pdf

Fonctions logarithme exponentielle et puissance. La fonction logarithme. La Variations et limites de th(x) th (x) = 1 ch. 2. (x). > 0. La fonction tangente ...

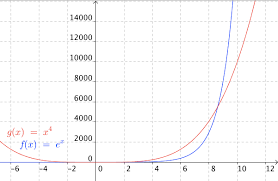FONCTION EXPONENTIELLE ET FONCTION LOGARITHME

b) Le nombre de bactéries a doublé à partir de 100 000 bactéries soit au bout d'environ 5h. V. Limites de la fonction exponentielle. 1) Limites aux bornes.

Tableaux des dérivées et primitives et quelques formules en prime

%20d%C3%A9riv%C3%A9es

Exponentielle et logarithme

logarithme (népérien) sont des fonctions réciproques : leurs courbes ... Croissance comparée et limites particulières lim x→−∞ xex = 0 lim x→+ ...

formulaire.pdf

Logarithme et Exponentielle : eln x = ln(ex) = x ln 1 = 0 ln(ab) = ln(a) + ln Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples f(x) f ...

FICHE : LIMITES ET ÉQUIVALENTS USUELS

FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. −−−−−→ x→+∞. 0 x lnx −−−−−→ x→0+. 0 ln(x) x −1. −−−→ x→1. 1 ln(1+ x) x.

Mathématiques générales pour la biologie

1.6 Fonctions logarithme et exponentielle décimaux . . . . . . . . . . 12. 2 Les limites usuelles ainsi que les propriétés opératoires ci-dessus

Fiche technique sur les limites

Comparaison de la fonction logarithme avec la fonction puissance en +? et en 0. En + ? lim x?+? ln(x) x. = 

FONCTION LOGARITHME NEPERIEN

La fonction logarithme népérien notée ln

Chapitre VII : Fonctions usuelles I La fonction logarithme

ln (xp) = p ln(x). ?. I.4 Limites remarquables. Exercice 2. Soit a ? R?. +.

Exponentielle et logarithme

Propriétés des logarithmes La fonction exponentielle (de base e) et la fonction logarithme (népérien) ... Croissance comparée et limites particulières.

formulaire.pdf

Logarithme et Exponentielle : eln x = ln(ex) = x Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples.

La fonction logarithme népérien

3 déc. 2014 Conclusion : la fonction ln est dérivable sur ]0; +?[ et (ln x)? = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...

FICHE : LIMITES ET ÉQUIVALENTS USUELS

FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? Comparaison des fonctions usuelles.

Des preuves de limites en logarithme - Un doc de Jérôme ONILLON

Conséquence graphique : l'axe des ordonnées est une asymptote à la courbe représentant ln. La preuve de ce théorème. ? La limite de ln en +?. Soit M un réel 

FONCTION EXPONENTIELLE ET FONCTION LOGARITHME

Remarque : Dans le cas de limites infinies la fonction exponentielle impose sa limite devant les fonctions puissances. Sa croissance est plus rapide. Exemple : 

La fonction logarithme décimal

La fonction x ?? log(x) s'appelle la fonction logarithme décimal. Limites lim x?0 x>0 log(x)=?? lim x?+? log(x)=+?. Propriétés algébriques.

FONCTION LOGARITHME NEPERIEN - maths et tiques

Propriété : La fonction logarithme népérien est dérivable sur ??0;+???et (lnx)'= 1 x Démonstration : La fonction ln est continue sur ??0;+??? donc pour tout réel a > 0 on a : lim x?a lnx=lna Donc par composée de limites en posant X=lnx: lim x?a lnx?lna x?a =lim X?lna X?lna eX?elna =lim X?lna 1 eX

Etude des limites de la fonction logarithme Fonction

Limites dans la fonction logarithme népérien Techniques de détermination de limites Rappelons d’abord les deux formules de base : = +? ?+? x x lim ln et = ?? ? x x lim ln 0 Une valeur utile : ln 1 = 0 Et les formules de croissance comparée : 0 ln lim = x?+? xn x et lim ln 0 0 = ? xn x x

FONCTION LOGARITHME NÉPÉRIEN - maths et tiques

Propriété : La fonction logarithme népérien est strictement croissante sur ]0 ; +?[ Démonstration : Pour tout réel +>0 (ln(+))#= ) >0 3) Limites aux bornes Propriétés : lim "?$ ln(+)=?? et lim "?&8 ln(+)=+? On dresse le tableau de variations de la fonction logarithme népérien :

Fonctions usuelles – Limites - Free

Fonctions usuelles – Limites I) Généralités • Dans tout ce cours I désignera un intervalle de Y (intervalle ouvert fermé semi-ouvert ) • Si I = [a b] on appellera I un segment de Y • On considère la fonction f allant de I dans Y telle que pour tout x de I il existe un unique réel y tel que y = f(x)

Searches related to limites usuelles logarithme PDF

FORMULAIRE Dans tout ce formulaire on ne parle pas du domaine de d´e?nition de la formule : par exemple ? a sous-entend a >0 n ? N? k est une constante Logarithme et Exponentielle : elnx = ln(ex) = x

Comment connaître les limites de la fonction logarithme ?

Voici un cours en terminale S sur les limites de la fonction logarithme. Inutile de vous le répéter, vous devez toutes les connaître. Mais la majorité sont faciles à retrouver sur le graphe de la fonction. Avec le tracé précédent, certaines limites se déduisent facilement.

Qu'est-ce que la fonction logarithme?

Comme on vient de le voir, la fonction logarithme est la fonction réciproque de la fonction exponentielle. Elle est donc très utile pour résoudre les équations comportant des puissances. Par exemple, la solution de l'équation est .

Comment calculer les logarithmes ?

Pour les autres racines, la fonction est roots (x) qui produira une matrice (voir section 3.1) contenant les racines. Pour calculer des logarithmes, il existe 3 fonctions : la fonction log (x) calcule les logarithmes naturels (ln), la fonction log2 (x) calcule les logarithmes en base 2, et la fonction log10 (x) calcule les logarithmes en base 10.

Quels sont les propriétés du logarithme ?

Les propriétés du logarithme et des exemples d'application. Ces égalités sont vraies pour tout M M, N N et b b pour lesquels le logarithme est défini, c'est-à-dire pour tout M M et N>0 N > 0 et tout 0 eq1 0 < b ?= 1. [Pourquoi ?] Vous devez savoir ce qu'est un logarithme. Si ce n'est pas le cas, cliquez ici.