 Fiche technique sur les limites
Fiche technique sur les limites
5 Fonctions logarithme et exponentielle. 5.1 Fonction logarithme. Comparaison de la fonction logarithme avec la fonction puissance en +∞ et en 0. En + ∞ lim.
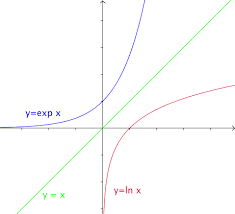 FONCTION LOGARITHME NEPERIEN
FONCTION LOGARITHME NEPERIEN
Remarque : Les fonctions puissances imposent leur limite devant la fonction logarithme népérien. a) Calculer les limites de f aux bornes de son ensemble de ...
 La fonction logarithme népérien
La fonction logarithme népérien
Dec 3 2014 Conclusion : la fonction ln est dérivable sur ]0; +∞[ et (ln x)′ = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...
 fonctions-usuelles.pdf
fonctions-usuelles.pdf
Fonctions logarithme exponentielle et puissance. La fonction logarithme. La Variations et limites de th(x) th (x) = 1 ch. 2. (x). > 0. La fonction tangente ...
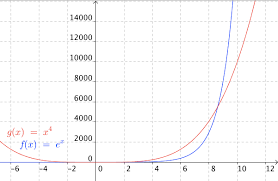 FONCTION EXPONENTIELLE ET FONCTION LOGARITHME
FONCTION EXPONENTIELLE ET FONCTION LOGARITHME
b) Le nombre de bactéries a doublé à partir de 100 000 bactéries soit au bout d'environ 5h. V. Limites de la fonction exponentielle. 1) Limites aux bornes.
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Exponentielle et logarithme
Exponentielle et logarithme
logarithme (népérien) sont des fonctions réciproques : leurs courbes ... Croissance comparée et limites particulières lim x→−∞ xex = 0 lim x→+ ...
 formulaire.pdf
formulaire.pdf
Logarithme et Exponentielle : eln x = ln(ex) = x ln 1 = 0 ln(ab) = ln(a) + ln Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples f(x) f ...
 FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. −−−−−→ x→+∞. 0 x lnx −−−−−→ x→0+. 0 ln(x) x −1. −−−→ x→1. 1 ln(1+ x) x.
 Mathématiques générales pour la biologie
Mathématiques générales pour la biologie
1.6 Fonctions logarithme et exponentielle décimaux . . . . . . . . . . 12. 2 Les limites usuelles ainsi que les propriétés opératoires ci-dessus
 Fiche technique sur les limites
Fiche technique sur les limites
Comparaison de la fonction logarithme avec la fonction puissance en +? et en 0. En + ? lim x?+? ln(x) x. =
 FONCTION LOGARITHME NEPERIEN
FONCTION LOGARITHME NEPERIEN
La fonction logarithme népérien notée ln
 Chapitre VII : Fonctions usuelles I La fonction logarithme
Chapitre VII : Fonctions usuelles I La fonction logarithme
ln (xp) = p ln(x). ?. I.4 Limites remarquables. Exercice 2. Soit a ? R?. +.
 Exponentielle et logarithme
Exponentielle et logarithme
Propriétés des logarithmes La fonction exponentielle (de base e) et la fonction logarithme (népérien) ... Croissance comparée et limites particulières.
 formulaire.pdf
formulaire.pdf
Logarithme et Exponentielle : eln x = ln(ex) = x Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples.
 La fonction logarithme népérien
La fonction logarithme népérien
3 déc. 2014 Conclusion : la fonction ln est dérivable sur ]0; +?[ et (ln x)? = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...
 FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? Comparaison des fonctions usuelles.
 Des preuves de limites en logarithme - Un doc de Jérôme ONILLON
Des preuves de limites en logarithme - Un doc de Jérôme ONILLON
Conséquence graphique : l'axe des ordonnées est une asymptote à la courbe représentant ln. La preuve de ce théorème. ? La limite de ln en +?. Soit M un réel
 FONCTION EXPONENTIELLE ET FONCTION LOGARITHME
FONCTION EXPONENTIELLE ET FONCTION LOGARITHME
Remarque : Dans le cas de limites infinies la fonction exponentielle impose sa limite devant les fonctions puissances. Sa croissance est plus rapide. Exemple :
 La fonction logarithme décimal
La fonction logarithme décimal
La fonction x ?? log(x) s'appelle la fonction logarithme décimal. Limites lim x?0 x>0 log(x)=?? lim x?+? log(x)=+?. Propriétés algébriques.
 FONCTION LOGARITHME NEPERIEN - maths et tiques
FONCTION LOGARITHME NEPERIEN - maths et tiques
Propriété : La fonction logarithme népérien est dérivable sur ??0;+???et (lnx)'= 1 x Démonstration : La fonction ln est continue sur ??0;+??? donc pour tout réel a > 0 on a : lim x?a lnx=lna Donc par composée de limites en posant X=lnx: lim x?a lnx?lna x?a =lim X?lna X?lna eX?elna =lim X?lna 1 eX
 Etude des limites de la fonction logarithme Fonction
Etude des limites de la fonction logarithme Fonction
Limites dans la fonction logarithme népérien Techniques de détermination de limites Rappelons d’abord les deux formules de base : = +? ?+? x x lim ln et = ?? ? x x lim ln 0 Une valeur utile : ln 1 = 0 Et les formules de croissance comparée : 0 ln lim = x?+? xn x et lim ln 0 0 = ? xn x x
 FONCTION LOGARITHME NÉPÉRIEN - maths et tiques
FONCTION LOGARITHME NÉPÉRIEN - maths et tiques
Propriété : La fonction logarithme népérien est strictement croissante sur ]0 ; +?[ Démonstration : Pour tout réel +>0 (ln(+))#= ) >0 3) Limites aux bornes Propriétés : lim "?$ ln(+)=?? et lim "?&8 ln(+)=+? On dresse le tableau de variations de la fonction logarithme népérien :
 Fonctions usuelles – Limites - Free
Fonctions usuelles – Limites - Free
Fonctions usuelles – Limites I) Généralités • Dans tout ce cours I désignera un intervalle de Y (intervalle ouvert fermé semi-ouvert ) • Si I = [a b] on appellera I un segment de Y • On considère la fonction f allant de I dans Y telle que pour tout x de I il existe un unique réel y tel que y = f(x)
 Searches related to limites usuelles logarithme PDF
Searches related to limites usuelles logarithme PDF
FORMULAIRE Dans tout ce formulaire on ne parle pas du domaine de d´e?nition de la formule : par exemple ? a sous-entend a >0 n ? N? k est une constante Logarithme et Exponentielle : elnx = ln(ex) = x
Comment connaître les limites de la fonction logarithme ?
Voici un cours en terminale S sur les limites de la fonction logarithme. Inutile de vous le répéter, vous devez toutes les connaître. Mais la majorité sont faciles à retrouver sur le graphe de la fonction. Avec le tracé précédent, certaines limites se déduisent facilement.
Qu'est-ce que la fonction logarithme?
Comme on vient de le voir, la fonction logarithme est la fonction réciproque de la fonction exponentielle. Elle est donc très utile pour résoudre les équations comportant des puissances. Par exemple, la solution de l'équation est .
Comment calculer les logarithmes ?
Pour les autres racines, la fonction est roots (x) qui produira une matrice (voir section 3.1) contenant les racines. Pour calculer des logarithmes, il existe 3 fonctions : la fonction log (x) calcule les logarithmes naturels (ln), la fonction log2 (x) calcule les logarithmes en base 2, et la fonction log10 (x) calcule les logarithmes en base 10.
Quels sont les propriétés du logarithme ?
Les propriétés du logarithme et des exemples d'application. Ces égalités sont vraies pour tout M M, N N et b b pour lesquels le logarithme est défini, c'est-à-dire pour tout M M et N>0 N > 0 et tout 0 eq1 0 < b ?= 1. [Pourquoi ?] Vous devez savoir ce qu'est un logarithme. Si ce n'est pas le cas, cliquez ici.
Mathématiques PTSI, Chapitre VII 2018-2019
Chapitre VII : Fonctions usuelles
I La fonction logarithme
I.1 Définition
Vous avez vu en lycée la construction de la fonction exponentielle comme l"unique solution de l"équation différentielle
f?-f= 0. Cependant l"existence était admise et relève d"un résultat que vous ne verrez qu"en seconde année. Notre
approche sera donc différente. Nous commençons par définir le logarithme et la fonction exponentielle constituera la
réciproque du logarithme.Nous verrons dans un prochain chapitre que sifest une fonction continue surIun intervalle deRet sia?I
alorsx?→Rxaf(t)dtest l"unique primitive defs"annulant ena. On appelle ce résultat le théorème fondamental de
l"analyse. Nous allons revoir ce résultat dans un exemple particulier pour construire le logarithme.
Pour toutp?Z\ {1},x?→xpadmet pour primitive la fonctionx?→xp+1p+1. Vous notez que seule la valeurp= 1
pose problème. Pourtant la fonctionx?→1x est continue surR?+. Ceci peut-être une motivation pour introduire la définition suivante.On appellelogarithme népérien, notéeln, la fonction définie par : ?x?R?+,ln(x) =Z x 11t dt.Définition I.1Remarques 1 :
•Par définition,ln(1) =R1 11t dt= 0.•Historiquement le logarithme népérien a été introduit pour la qualité de ses propriétés algébriques transformant
un produit en somme. En l"absence d"ordinateur, le calcul une somme est nettement plus aisé que le calcul d"un
produit.I.2 Continuité et dérivabilitéLa fonction logarithme est continue et dérivable surR?+. De plus pour toutx?R?+,
ln ?(x) =1x .Proposition I.2 Démonstration.Continuité.Soitx?R?+. On a pour touth?]-x;+∞[, ln(x+h)-ln(x) =Z x+h 11t dt-Z x 11t dt=Z x+h x1t dt.Premier cash>0. Par positivité de la fonction inverse surR?+, on sait queln(x+h)-ln(x)>0. De plus par
décroissance de la fonction inverse surR?+, on a06ln(x+h)-ln(x) =Z
x+h x1t dt6Z x+h x1x dt=hxDeuxième cash60, alorsln(x+h)-ln(x) =-Rx
x+h1t dt60. De plus par décroissance de la fonction inverse sur R ?+, (attention au signe moins qui inverse l"inégalité)0>ln(x+h)-ln(x)>-Z
x x+h1x dt=hx 1Mathématiques PTSI, Chapitre VII 2018-2019
Ainsi, on obtient que
|h|x6ln(x+h)-ln(x)6|h|x
Donc par le théorème d"encadrement, quandh→0, on obtient lim h→0ln(x+h)-ln(x) = 0.Donc la fonction logarithme est continue enx. Ceci étant vraie pour toutx?R?+, on en déduit quelnest continue
surR?+.Dérivabilité.On affine nos précédentes inégalités. Fixonsx?R?+. Pour touth?]-x;+∞[\{0}, notons d"abord que
1x =1h R x+h x1x dt. Ainsi, 1x -ln(x+h)-ln(x)h =1h Z x+h x1x dt-1h Z x+h x1t dt=1h Z x+h x1x -1t dt=1h Z x+h xt-xtx dt. Donc, sih >0,06t-x6hpour toutt?[x;x+h]. Orhxt >0pour toutt?[x;x+h]Donc 061x-ln(x+h)-ln(x)h 61h
Z x+h xhtx dt=1x Z x+h x1t dt.
Or nous avons déjà vu que pourh >0,Rx+h
x1t dt6hx . Donc 061x-ln(x+h)-ln(x)h 6hx 2. En procédant de même, on peut montrer que, sih <0, 0>1x -ln(x+h)-ln(x)h >hx 2.
Donc globalement, pour touth?]-x;+∞[\{0},
|h|x 261x-ln(x+h)-ln(x)h 6|h|x 2
Et par encadrement, on en déduit que
lim 1x -ln(x+h)-ln(x)h = 0?limh→0ln(x+h)-ln(x)h =1x Donc la fonction logarithme est dérivable et sa dérivée est donnée par ?x?R?+,ln?(x) =1x Exercice 1. Calculer la dérivée de la fonctionf:¨]-1;1[→R x?→ln1+x1-x .La fonction logarithme est strictement croissante surR?+.Corollaire I.3Démonstration.C"est une conséquence directe de la stricte positivité de sa dérivée surR?+.
2Mathématiques PTSI, Chapitre VII 2018-2019
I.3 Propriétés algébriques
Soientx?]0;+∞[,y?]0;+∞[etp?Z.
1.ln(xy) = ln(x) + ln(y). 2.ln1x
=-ln(x).3.lnxy
= ln(x)-ln(y). 4.ln(xp) =pln(x).Proposition I.4Démonstration.
1. Soit y >0un réel fixé. Considérons la fonctiong:¨R?+→R x?→ln(xy)-ln(x)-ln(y). La fonctiongest dérivable surR?+comme somme et composée de fonctions dérivables et pour toutx >0, g ?(x) =yxy -1x = 0. Donc la fonctiongest constante. De plus pourx= 1, on ag(1) = ln(y)-ln(1)-ln(y) = 0. Donc pour tout x >0,ln(xy)-ln(x)-ln(y) = 0. 2.Soit x >0. Le réely=1x
est aussi strictement positif. Donc d"après le point précédent,ln(xy) = ln(1) = 0 = ln(x) + ln(y) = ln(x) + ln1x . Doncln1x =-ln(x). 3. Soit x >0ety >0, on a, en utilisant le point 1,lnxy= lnx×1y
= ln(x) + ln1y
. En utilisant alors le
point 2,lnxy= ln(x)-ln(y).
4.Fixons x >0et pour toutn?N, considérons la propositionPn: "ln(xn) =nln(x)». Démontrons quePnest
vraie pour toutn?Npar récurrence. •Sin= 0, alorslnx0= ln(1) = 0 = 0×ln(x). DoncP0est vraie. •Soitn?N. Supposons quePnest vraie. Alors, d"après le point 1 avecy=xn>0, ln xn+1= ln(x×xn) = ln(x) + ln(xn).PuisquePnest vraie,
lnxn+1= ln(x) +nln(x) = (n+ 1)ln(x). DoncPn+1est vraie. Nous avons donc montré quePn?Pn+1. •Au bilan, on conclut quePnest vraie pour toutn?N.Soit maintenantp?Z\N. Puisque-p?N, par ce qui précèdeln(x-p) =-pln(x). Or d"après le point 2,
ln(x-p) = ln1x p=-ln(xp). Donc-ln(xp) =-pln(x)?ln(xp) =pln(x). Conclusion, pour toutp?Z, ln(xp) =pln(x).I.4 Limites remarquables
Exercice 2. Soita?R?+. Discuter suivant les valeurs deade la limite de la suite(ln(an))n?N.La fonction logarithme vérifie les limites remarquables suivantes.
1.limx→+∞ln(x) = +∞. 2.limx→0ln(x) =-∞. 3.limx→+∞ln(x)x
= 0. 4.limx→0xln(x) = 0.5.limx→0ln(1+x)x
= 1.Proposition I.5Démonstration.
3Mathématiques PTSI, Chapitre VII 2018-2019
1.Puisque la fonction logarithme est strictemen tcroissan te,soit la fonction logarithme con vergev ersune limite
l?R?+soit la fonction logarithme diverge vers+∞(mais ne peut pas avoir de par sa croissance un comportement
plus exotique comme une oscillation quelconque). Ce résultat de la limite monotone est intuitif mais sera
démontré dans un chapitre ultérieur. Démontrons que le logarithme n"est pas borné c"est à dire que pour tout
M >0, il existex?R?+tel queln(x)> M. FixonsM >0. Pour toutn?N, on a (cf propriété précédente)
ln(2n) =nln(2)-→n→+∞+∞. Donc il existen0?Ntel quen0ln(2)> M. Donc en prenantx= 2n0, on a bien
trouvé un réel tel queln(x)> M. Ainsi la fonction logarithme est non-bornée et croissante et donc
lim x→+∞ln(x) = +∞. 2.P ourtout x >0,ln(x) =-ln1x
. Donc limOrlimx→0x>01x
= +∞. Donc par composition de limites et le point précédent,limx→0x>0ln(x) =-∞. 3.P osonsg:¨R?+→R
x?→ln(x)x . La fonctiongest bien définie et dérivable surR?+. De plus pour toutx?R?+, g ?(x) =1x×x-ln(x)x
2=1-ln(x)x
2. Doncg?(x)>0?1-ln(x)>0?1>ln(x). La fonction logarithme est continue et strictement croissantesur[1;+∞[,ln(1) = 0etlimx→+∞ln(x) = +∞. Donc d"après le théorème de la bijection,ln([1;+∞[) = [0;+∞[
et même il existe un unique réel, notons-leetel queln(e) = 1. Ainsig?(x)>0?ln(e)>ln(x). Par croissance
de la fonction logarithme, on en déduit queg?(x)>0?e>x. De plusg(e) =1e . On obtient donc le tableau de variation deg:x g ?(x)x?→g(x)0e+∞-0+ 1 e1 e On constate que la fonction est majorée et admet même un maximum lorsquex= equi vaut1e . Donc pour tout x >0, ln(x)x 61eNotons que par croissance de la fonction logarithme, pour toutx >1,ln(x)x >0. Donc pour toutx >1,
06ln(⎷x)2(
⎷x)2=2⎷x×ln(⎷x)⎷x
62⎷x
×1e
Finalement, par le théorème d"encadrement, on en déduit que lim x→+∞ln(x)x = 0. 4.L"idée est exactemen tla même que p ourdémon trerle p oint2, en p osantle c hangementde v ariableu=1x
lim x→0xln(x) = limu→+∞1u =-limu→+∞ln(u)u = 0. 4Mathématiques PTSI, Chapitre VII 2018-2019
5. On reconnaît la dériv éede la fon ctionlogarithme en 1: lim x→0ln(1 +x)x = limx→0ln(1 +x)-ln(1)x = ln?(1) = 1.Remarque 2 :Au cours de la démonstration, nous avons démontré le résultat suivant : il existe un unique réel
e?]0;+∞[tel queln(e) = 1. Ce nombre s"appelle la constante de Neper.Le graphe de fonction logarithme a
•une asymptote verticalex= 0en0, •une tangente d"équationy=x-1au point(1;0), •une branche parabolique de direction(Ox)en+∞.Corollaire I.6I.5 Graphe et variations
De notre étude précédente, on en déduit le tableau de variation suivant :xAinsi que son graphe :
123456
-4-3-2-112ln y=x-1eII La fonction exponentielle
II.1 Définition et premières propriétésLa fonction logarithme est continue, strictement croissante sur]0;+∞[etf(]0;+∞[) =R. Donc d"après le théorème
de la bijection, la fonction logarithme est une bijection de]0;+∞[dansR. 5Mathématiques PTSI, Chapitre VII 2018-2019
On appellefonction exponentielle, notéexp, la fonction réciproque du logarithme népérien :exp:R→]0;+∞[.Définition II.1
•La fonction exponentielle est strictement croissante surRet réalise une bijection deRdans]0;+∞[.
•La fonction exponentielle est continue et dérivable surR. De plus pour toutx?R, exp ?(x) = exp(x).Proposition II.2Démonstration.Le théorème de la bijection appliqué à la fonction logarithme assure que la fonction exponentielle
est une fonction continue, strictement croissante surRet réalise une bijection deRdans]0;+∞[. De plus pour tout
x?R?+,ln?(x) =1x>0. Donc d"après le théorème de la dérivée de la fonction réciproque, on sait que la fonction
exponentielle est dérivable surlnR?+=Ret pour toutx?R, exp ?(x) =1ln ?(exp(x))= exp(x).Soit(x,y)?R2,
1.exp(x+y) = exp(x)exp(y)2.exp(-x) =1exp(x)
3.exp(x-y) =exp(x)exp(-y)4.?p?Z,exp(px) = (exp(x))p.Proposition II.3
Démonstration.Soit(x,y)?R2, en utilisant les propriétés du logarithme, on aln(exp(x)exp(y)) = ln(exp(x)) +
ln(exp(y)) =x+y. Donc en composant par l"exponentielle, on obtient queexp(ln(exp(x)exp(y))) = exp(x)exp(y) =
exp(x+y). En procédant de même, on établit les autres affirmations.Rappelons que par définition,eest l"unique réel tel queln(e) = 1. De plus la fonction exponentielle est la fonction
qui à tout réel associe son unique antécédent par le logarithme. Donc en particulierexp(1) = e.Pour toutx?R, on noteex= exp(x). La fonction exponentielle est donc notéex?→ex.Notation
Remarque 3 :La notation est compatible avec la fonction puissance sur les entiers naturels. En effet, pour tout
n?N, e n= e×e×··· ×e|{z} nfois= exp(n).En effet d"après la proposition précédenteexp(n) = exp(n×1) = (exp(1))n= en. Elle est de même compatible avec
la fonction puissance sur les entiers relatifs. II.2 Limites remarquablesLa fonction exponentielle admet les limites remarquables suivantes.1.limx→+∞ex= +∞. 2.limx→-∞ex= 0. 3.limx→+∞e
xx = +∞. 4.limx→-∞xex= 0.5.limx→0e
x-1x = 1.Proposition II.4 6Mathématiques PTSI, Chapitre VII 2018-2019
Démonstration.Les limites aux bornes de la fonction exponentielle sont des conséquences du théorème de la
bijection. Redémontrons-les d"une autre façon. 1. Mon tronsque p ourtout x?R,ex>x+1. Posonsg(x) = ex-x-1pour toutx?R. La fonctiongest définie, continue et dérivable surRcomme somme de fonctions dérivables surRet pour toutx?R, g ?(x) = ex-1. La fonction exponentielle est strictement croissante surRete0= 1(carln(1) = 0). Donc pour toutx>0, ex>1et pour toutx60,ex61. On en déduit le tableau de variation de la fonctiongque l"on complète avec
la valeurg(0) = e0-1 = 0.x g ?(x)x?→g(x)-∞0+∞-0+ 00En conséquence, pour toutx?R,g(x)>0et doncex>1 +x. Par comparaison, on en déduit quelimx→+∞ex=
2. Lorsque x→ -∞, on au=-x→+∞. Donc lim x→-∞ex= limu→+∞e-u= limu→+∞1e u= 0. 3. On a vu dans le p oint1 que p ourtou tx?R,ex>x+ 1>x. Doncexx >1pour toutx >0ou encoreex2 x 2 >1 pour toutx >0. Alors e xx = ex2 ex2 x =ex2 2 e x2 x 2 >ex2 2 Dans la dernière inégalité, nous avons utilisé la positivité de ex2 2 . Orlimx→+∞ex2 2 = +∞, donc par comparaison, lim x→+∞e xx 4.A l"aide d uc hangementde v ariableu=-x,
lim x→-∞xex= limu→+∞-ue-u=-limu→+∞ue u= 0. 5. On reconnait le taux d"accroissemen tde la fon ctionexp onentielleen 0: lim x→0e x-1x = exp?(0) = exp(0) = 1.Le graphe de fonction exponentielle a
quotesdbs_dbs11.pdfusesText_17[PDF] la pyramide du louvre est une pyramide régulière à base carrée
[PDF] géométrie collège
[PDF] mélange des couleurs en peinture pdf
[PDF] tableau de conversion longueur ce2
[PDF] modèle de fiche d'évaluation des fournisseurs
[PDF] critères de sélection d'un fournisseur
[PDF] procedure selection fournisseur
[PDF] on considère la pyramide sabcd de sommet s
[PDF] regle puissance exponentielle
[PDF] rubriques nomenclature loi sur l'eau
[PDF] nomenclature eau
[PDF] indice de pollution par ville
[PDF] fonction puissance cours
[PDF] nomenclature loi sur l'eau 2017
