[PDF] Fonctions usuelles Reprendre les questions précé

View - Download Fonctions usuelles

Previous PDF

Next PDF

Exo7

Fonctions usuelles

* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours

Exercice 1**I1.Soit fune fonction dérivable surRà valeurs dansR. Montrer que sifest paire,f0est impaire et sifest

impaire,f0est paire. 2.

Soient n2Netfune fonctionnfois dérivable surRà valeurs dansR.f(n)désignant la dérivéen-ième

def, montrer que sifest paire,f(n)est paire sinest pair et impaire sinest impair. 3. Soit fune fonction continue surRà valeurs dansR. A-t-on des résultats analogues concernant les primitives def? 4.

Reprendre les questions précédentes en remplaçant la condition fest paire (ou impaire) par la condition

festT-périodique . npn,n2N. et tracer son graphe. 2. T rouvertous les couples (a;b)d"entiers naturels non nuls et distincts vérifiantab=ba. Résoudre dansRles équations ou inéquations suivantes :

1.()lnjx+1jlnj2x+1j6ln2,

2.()xpx

=px x,

3.()2argshx=argch3argth79

4.()lnx(10)+2ln10x(10)+3ln100x(10) =0,

5.()22x3x12

=3x+12 22x1.
1 x!+¥(xx)xx (xx).

Construire le graphe des fonctions suivantes :

1. (*) f1(x) =2j2x1jjx+2j+3x. 2. (**) f2(x) =ln(chx). 3. (***) f3(x) =x+pjx21j. 4. (**) f4(x) =jtanxj+cosx. 5. (***) f5(x) =1+1x x(à étudier sur]0;+¥[). 6. (**) f6(x) =log2(1log12 (x25x+6)).

Correction del"exer cice1 N1.Soit fune fonction dérivable surRà valeurs dansR. Sifest paire, alors, pour tout réelx,f(x)=f(x).

En dérivant cette égalité, on obtient

8x2R;f0(x) =f0(x);

et doncf0est impaire. De même, sifest impaire, pour tout réelx, on af(x) =f(x), et par dérivation

on obtient pour tout réelx,f0(x) =f0(x).f0est donc paire.

(fpaire)f0impaire) et(fimpaire)f0paire.)2.Soient n2Netfune fonctionnfois dérivable surRà valeurs dansR. Supposonsfpaire. Par suite,

pour tout réelx,f(x) =f(x). Immédiatement par récurrence, on a

8x2R;f(n)(x) = (1)nf(x):

Ceci montre quef(n)a la parité den, c"est-à-dire quef(n)est une fonction paire quandnest un entier pair

et est une fonction impaire quandnest un entier impair. De même, sifest impaire etnfois dérivable sur

R,f(n)a la parité contraire de celle den.

3. Soit fune fonction continue surRet impaire etFune primitive def. Montrons queFest paire. Pourx réel, posonsg(x) =F(x)F(x).gest dérivable surRet pour tout réelx, g

0(x) =F0(x)+F0(x) =f(x)+f(x) =0:

gest donc constante surRet par suite, pour tout réelx,g(x) =g(0) =F(0)F(0) =0. Ainsi,gest

la fonction nulle et donc, pour tout réelx,F(x) =F(x). On a montré queFest paire. Par contre, si

fest paire,Fn"est pas nécessairement impaire. Par exemple, la fonctionf:x7!1 est paire, mais F:x7!x+1 est une primitive defqui n"est pas impaire. 4.

On montre aisément en déri vantune ou plusieurs fois l"ég alité: 8x2R;f(x+T)=f(x), que les dérivées

successives d"une fonctionT-périodique sontT-périodiques. Par contre, il n"en est pas de même des

primitives. Par exemple, si pour tout réelx,f(x) =cos2x=12 (1+cos(2x)),festp-périodique, mais la fonctionF:x7!x2 +sin(2x)4 , qui est une primitive defsurR, n"est pasp-périodique ni même périodique

tout court.Correction del"exer cice2 NPourn2N, posonsun=npnpuis, pourxréel strictement positif,f(x) =x1=xde sorte que pour tout naturel

non nuln, on aun=f(n).fest définie sur]0;+¥[et pourx>0,f(x) =elnx=x.fest dérivable sur]0;+¥[et

pourx>0, f

0(x) =1lnxx

2elnx=x:

Pourx>0,f0(x)est du signe de 1lnxet doncf0est strictement positive sur]0;e[et strictement négative sur

]e;+¥[.fest donc strictement croissante sur]0;e]et strictement décroissante sur[e;+¥[. En particulier, pour

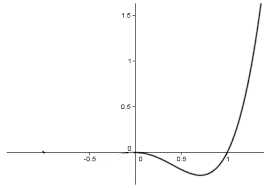
n>3, u n=f(n)6f(3) =u3=3p3: Commeu2=p2>1=u1, on a donc Maxfun;n2Ng=Maxfp2;3p3g. Enfin,p2=1;41::: <1;44::=3p3 (on peut aussi constater que(p2)6=8<9= (3p3)6). Finalement, 3 Max fnpn;n2Ng=3p3=1;44:::Correction del"exer cice3 N1.Pour x>0, posonsf(x) =lnxx .fest définie et dérivable sur]0;+¥[et, pourx>0,f0(x) =1lnxx

2.fest

donc strictement croissante sur]0;e]et strictement décroissante sur[e;+¥[. Le graphe defs"en déduit

facilement :1 2 3 4 -1 -2 -3 -4 1 e e2.Soient aetbdeux entiers naturels non nuls tels quea3, puisquefest strictement décroissante sur[e;+¥[, on a alorsf(a)>f(b)et en particulier, f(a)6=f(b).an"est donc pas solution.a=1 n"est évidemment pas solution. Par exemple,ab=ba) 1 b=b1)b=1=ace qui est exclu. Donc, nécessairementa=2 etbest un entier supérieur ou égal

à 3, et donc àe, vérifiantf(b) =f(2). Commefest strictement décroissante sur[e;+¥[, l"équation

f(b) =f(2)a au plus une solution dans[e;+¥[. Enfin, comme 24=16=42, on a montré que : il existe

un et un seul couple(a;b)d"entiers naturels non nuls tel quea lnjx+1jlnj2x+1j6ln2,lnx+12x+1

6ln2,x+12x+1

62 etx+16=0

, 26x+12x+162 etx6=1,x+12x+1+2>0 etx+12x+1260 etx6=1

5x+32x+1>0 et3x12x+160 etx6=1

x2

¥;35

12 et

¥;12

13 etx6=1 ,x2]¥;1[[ 1;35 13 2.

Pour x>0

x px =px x,pxlnx=xlnpx,lnx(pxx2 ) =0 ,lnxpx(2px) =0,x=1 oux=4: 4

3.ar gch3=ln(3+p3

21) =ln(3+p8)et argth79

=12 ln1+79 179
=lnp8. Donc, argch3argth79 ln 1+3p8 . Par suite,

2argshx=argch3argth79

,x=sh12 ln 1+3p8 ,x=12 0 @s1+3p8 1q 1+3p8 1 A =32 p8 1q 1+3p8 =32 4p8 1p 3+2p2 ,x=34p2 4 1q (1+p2)2=34p2(p21)4 4.

Pour x2]0;+¥[n1100

;110 ;1, ln x(10)+2ln10x(10)+3ln100x(10) =0,ln(10)lnx+2ln(10)ln(10x)+3ln(10)ln(100x)=0 ,6ln2x+10ln(10)lnx+2ln2(10) =0 ,lnx28 :5ln(10)+q13ln

2(10)6

;5ln(10)q13ln

2(10)6

9 ,x2n

10(5p13)=6;10(5+p13)=6o

Comme aucun de ces deux nombres n"est dans

1100
;110 ;1,S=n 10 (5p13)=6;10(5+p13)=6o 5.

Soit x2R.

2

2x3x12

=3x+12

22x1,22x+22x1=3x+12

+3x12 ,22x1(2+1) =3x12 (3+1),322x1=43x12 ,22x3=3x32 ,(2x3)ln2= x32 ln3 ,x=3ln232 ln32ln2ln3,x=32 :Correction del"exer cice5 NPourx>0,(xx)x=exln(xx)=ex2lnxetx(xx)=exxlnx. Par suite,

8x>0;(xx)xx

(xx)=exp(lnx(x2xx)): Or,x2xx=xx(1x2x)=exlnx(1e(2x)lnx). Quandxtend vers+¥,(2x)lnxtend vers¥. Donc, 1 e (2x)lnxtend vers 1 puisx2xxtend vers¥. Mais alors, lnx(x2xx)tend vers¥, puis(xx)xx (xx)=exp(lnx(x2 x x))tend vers 0. lim x!+¥(xx)xx (xx)=0:5 Correction del"exer cice6 NOn noteraCile graphe defi.

1.f1est définie et continue surR, dérivable surRn2;12

. On précise dans un tableau l"expression de f

1(x)suivant les valeurs dex.x¥2 1=2+¥j2x1j2x+12x+12x1jx+2jx2x+2x+2f

1(x)42x6x4On en déduitC1.1 2 3-1-2-3-4-5

12345678

-1 y= 4 y=-2x y= 6x-4 1

22.Soit x2R. chx>1 et doncf2(x)existe etf2(x)>0.f2est donc définie surR. De plus,f2est continue

et dérivable surR, paire. Puisque la fonctionx7!chxest strictement croissante surR+à valeurs dans

]0;+¥[et que la fonctionx7!lnxest strictement croissante sur]0;+¥[,f2est strictement croissante sur

R

+et, par parité, strictement décroissante surR.f2est paire et doncf02est impaire. Par suite,f02(0)=0

etC2admet l"axe des abscisses pour tangente en(0;f2(0)) = (0;0).Etude en+¥. Pourx>0, f

2(x) =ln12

(ex+ex)) =ln(ex+ex ln2=ln(ex(1+e2x))ln2=xln2+ln(1+e2x): Quandxtendvers+¥,e2xtendvers0etdonc, ln(1+e2x)tendvers0. Onendéduitquelimx!+¥f2(x)= +¥. De plus, limx!+¥(f2(x)(xln2)) =0 et la droite(D)d"équationy=xln2 est asymptote àC2

en+¥. Par symétrie par rapport à la droite(Oy), la droite(D0)d"équationy=xln2 est asymptote à

C

2en¥. Enfin, pour tout réelx,

f

2(x)(xln2) =ln(1+e2x)>ln1=0;

etC2est strictement au-dessus de(D)surR. De même,C2est strictement au-dessus de(D0)surR. On en déduitC2. 6

1 2 3-1-2-3-4

123
-13.f3est définie et continue surR, dérivable surRnf1;1g.Etude en¥. Soitx61. f

3(x) =x+px

21=(x+px

21)(xpx

21)xpx

21=1xpx

21:

Or, quandxtend vers¥,xpx

21 tend vers¥et donc limx!¥f3(x) =0.Etude en+¥.

Immédiatement, lim

x!+¥f3(x) = +¥. Ensuite, pourx>1, f 3(x)x =x+px 21x
=1+r11x 2; qui tend vers 2 quandxtend vers+¥. Mais alors, f

3(x)2x=x+px

21=(x+px

21)(xpx

21)xpx

21=1x+px

21:

On en déduit que lim

x!+¥(f3(x)2x) =0 et donc que la droite(D)d"équationy=2xest asymptote à C

3en+¥.Etude en1. Pourx>1,

f

3(x)f3(1)x1=(x1)+p(x1)(x+1)x1=1+rx+1x1;

et pourx2]1;1[, f

Par suite, lim

x!1;x>1f3(x)f3(1)x1= +¥et limx!1;x<1f3(x)f3(1)x1=¥. On en déduit quef3n"est pas

dérivable en 1, mais queC3admet deux demi-tangentes parallèles à(Oy)au point deC3d"abscisse 1.

Les résultats sont analogues en1.Etude des variations de f3. Pourx2]¥;1[[]1;+¥[,f3(x) = x+px

21 et donc

f

03(x) =1+xpx

21=x+px

21px
21:

Six>1, on ax+px

21>0 et donc,f03(x)>0. Six<1, on a

px 21

2=jxj=x;

et donc,x+px

21<0 puisf03(x)<0. Ainsi,f3est strictement décroissante sur]¥;1[et strictement

croissante sur]1;+¥[. Pourx2]1;1[,f3(x) =x+px2+1 et donc 7 f

03(x) =1xpx2+1=px2+1xpx2+1:

Six2]1;0], on a clairementf03(x)>0. Si x2[0;1[, par stricte croissance de la fonctionx7!x2surR+, on a x):

Donc,f03est strictement positive surh

0;1p2 h , strictement négative suri1p2 ;1h et s"annule en1p2 . En résumé,f03est strictement négative sur]¥;1[et suri1p2 ;1h et strictement positive suri 1;1p2 h et sur]1;+¥[.f3est donc strictement croissante sur]¥;1]et surh1p2 ;1h et strictement décroissante surh 1;1p2 i et sur[1;+¥[. On en déduitC3.1 2 3-1-2-3-4 12345
-1 1p2p 2 y= 2x4.f4est définie surRnp2 +pZ, 2p-périodique et paire. On étudie doncf4sur0;p2 [p2 ;p.Etude des variations de f

4. Pourx20;p2

,f4(x) =tanx+cosxet donc, f

04(x) =1cos

2xsinx>11=0;

avec égalité si et seulement si sinx=cos2x=1 ce qui est impossible. Donc,f04est strictement positive

sur0;p2 etf4est strictement croissante sur0;p2 . Pourx2p2 ;p,f4(x) =tanx+cosxetf4est strictement décroissante surp2 ;pen tant que somme de deux fonctions strictement décroissantes surp2 ;p. On a immédiatement limx!p2 x4(x) =limx!p2 x>p2 f

4(x) = +¥. On en déduitC4.

8

1 2 3 4 5 6 7-1-2-3-4-5-6-7-8

12345
-1 -π2π23π2-3π25.Soit x>0.xn"est pas nul donc1x existe puis 1+1x >0 etf6(x)existe.Etude en 0:Pourx>0,xln(1+ 1x ) =xlnx+xln(1+x). Par suite,xln(1+1x )tend vers 0 quandxtend vers 0 par valeurs supérieures et doncf5(x) =exp(xln(1+1x ))tend vers 1. Posons encoref5(0) =1 et étudions la dérivabilité def5en 0.

Pourx>0,

f

5(x)f5(0)x0=1x

exp(xln(1+1x ))1 =expxln(1+1x )1xln1+1x ln 1+1x

Or,xln1+1x

tend vers 0 quandxtend vers 0, et donc lim x!0x>0exp(xln1+1x )1xln1+1x =limy!0e y1y =1:

D"autre part, ln

1+1x tend vers+¥quandxtend vers 0 par valeurs supérieures. Finalement, lim x!0x>0f

5(x)f5(0)x0= +¥:

Ainsi,f5n"est pas dérivable en 0 maisC5admet l"axe des ordonnées pour tangente en(0;f5(0))=(0;1).

Etude en+¥:Pourx>0,xln1+1x

=ln(1+1x )1x et donc limx!+¥xln1+1x =limy!0ln(1+y)y =1. Par suite, lim x!+¥f5(x) =e:

Etude des variations de f

5:Pourx>0,f5(x)>0 puis ln(f5(x)) =xln(1+1x

). Par suite, pourx>0, f

05(x) =f5(x)ln(f5)0(x) =f5(x)

ln 1+1x +x(1x

2)1+1x

=f5(x)g(x); oùg(x) =ln1+1x

11+x. Sur]0;+¥[,f05est du signe deg. Pour déterminer le signe deg, étudions

d"abord les variations degsur]0;+¥[.gest dérivable sur]0;+¥[et pourx>0, g

0(x) =1x

21+1x
+1(x+1)2=1x(x+1)+1(x+1)2=1x(x+1)2<0:

gest donc strictement décroissante sur]0;+¥[, et puisque limx!+¥g(x) =0,gest strictement positive

sur]0;+¥[. Il en est de même def05.f5est strictement croissante sur]0;+¥(. On en déduitC5.

9

1 2 3 4 5 6 7

12 e6.Domaine de définition de f6:Soitx2R.quotesdbs_dbs35.pdfusesText_40

[PDF] ensemble de definition exp et ln

[PDF] exp(a)+exp(b)

[PDF] exp(-0)

[PDF] comment déterminer le domaine de définition d'une fonction

[PDF] fonction ln domaine de définition

[PDF] exp(-1)

[PDF] exercices corrigés domaine de définition d'une fonction pdf

[PDF] comment déterminer l'image d'une fonction

[PDF] comment trouver le domaine d'une fonction

[PDF] ensemble image maths

[PDF] loi organique des communes maroc

[PDF] loi organique 113-14 sur les communes maroc

[PDF] projet de loi organique 113-14 sur les communes

[PDF] les branches de linformatique pdf

[PDF] oiq salaire ingénieur junior