 Carrés magiques
Carrés magiques
Les diagonales permettent de déterminer deux nouvelles cases. On voit ainsi de proche en proche
 Le carré magique
Le carré magique
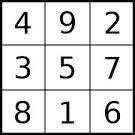
Sujet: Le but du carré magique 3x3 est de remplir un carré avec tous les chiffres de 1 à 9. Mais attention : chaque nombre ne doit apparaître qu'une seule
 Le CoatrEvent
Le CoatrEvent
22 mars 2022 Les élèves de la classe de CM1-CM2 de l'école de Coatréven se sont ... Le Carré Magique est une salle de spectacle. Il peut accueillir 850 ...
 Fichier-CARRES-MAGIQUES.pdf
Fichier-CARRES-MAGIQUES.pdf
1. 2. 3. 4. 5 6. 7. 8. 9. 10 11. CARRES MAGIQUES. 1. 12 12 12 12. Utilise les nombres : . . . 12. 01
 RALLYE LATHEMATIQUE 2011/2012 1ère Manche CM1
RALLYE LATHEMATIQUE 2011/2012 1ère Manche CM1
Dans un carré magique les sommes des nombres de chaque ligne
 FICHE RESOLUTION DE PROBLEMES N° ___
FICHE RESOLUTION DE PROBLEMES N° ___
Dans un carré magique les sommes des nombres de chaque ligne
 velo tt temps enfant 2011-2012
velo tt temps enfant 2011-2012
CM1 CM 2. Projet vélo par tous les temps de l'enfant. Page 2. 2. Sommaire Autres situations possibles : Accroche à deux carré magique
 Les-Carrés-Magiques-CP-CE1-CE2.pdf
Les-Carrés-Magiques-CP-CE1-CE2.pdf
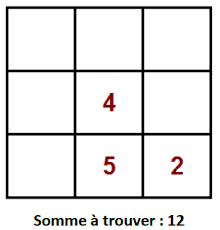
Les Carrés Magiques. Fonctionnement du carré magique : Tu dois trouver le même nombre (la même somme) : -en additionnant les trois nombres qui sont sur
 LE CARRÉ MAGIQUE POUR LES COLLÉGIENS Saison 2022-2023
LE CARRÉ MAGIQUE POUR LES COLLÉGIENS Saison 2022-2023
Dispositifs Carré Très Curieux : 21€ par élève pour les 3 spectacles du parcours 7€ par spectacle supplémentaire si vous désirez le compléter. CM1
 RALLYE LATHEMATIQUE 2011/2012 1ère Manche CM1
RALLYE LATHEMATIQUE 2011/2012 1ère Manche CM1
3.Le carré magique sur 10 points. Complète le carré magique avec les cartes Les nouvelle souris grignoteuse (10 points). Le dessin correspondant à la tablette ...
 Carrés magiques
Carrés magiques
Les diagonales permettent de déterminer deux nouvelles cases. On voit ainsi de proche en proche
 Les carrés magiques
Les carrés magiques
Un carré magique comme les deux exemples qui précèdent
 Le carré magique
Le carré magique
Sujet: Le but du carré magique 3x3 est de remplir un carré avec tous les chiffres de 1 à 9. Mais attention : chaque nombre ne doit apparaître qu'une seule
 Carrés magiques - Laddition
Carrés magiques - Laddition
L'addition. Carrés magiques. Un carré magique est un tableau dans lequel les sommes des lignes colonnes et diagonales principales sont égales.
 FICHE RESOLUTION DE PROBLEMES N° ___
FICHE RESOLUTION DE PROBLEMES N° ___
Dans un carré magique les sommes des nombres de chaque ligne
 199 défis (mathématiques) à manipuler !
199 défis (mathématiques) à manipuler !
Carré magique. Place les jetons 1 2
 Fichier-CARRES-MAGIQUES.pdf
Fichier-CARRES-MAGIQUES.pdf
CARRES MAGIQUES. 1. 2. 3. 4. 5 6. 7. 8. 9. 10 11. CARRES MAGIQUES. 1. 12 12 12 12. Utilise les nombres : . . . 12. 01
 Untitled
Untitled
Ce petit ouvrage présente des problèmes que les élèves des classes de CM1 A et B de l'école Camus Voici ce qu'on appelle un carré magique.
 1 - Complète les carrés magiques suivants (un carré est magique si
1 - Complète les carrés magiques suivants (un carré est magique si
1 - Complète les carrés magiques suivants (un carré est magique si les sommes en lignes en colonnes et en diagonales sont égales).
 Rallye mathématique Epreuve 1 – CM1 - Réponses
Rallye mathématique Epreuve 1 – CM1 - Réponses
ENIGME 6 : Magique carré (10 points). ? Compléter le carré magique. Les sommes sur chaque ligne chaque colonne et chaque diagonale doivent être égales à
 [PDF] Carrés magiques
[PDF] Carrés magiques
Un carré magique (de dimension 4) contient les nombres entiers de 1 à 16 Ils sont disposés de telle façon que les sommes en ligne en colonne et selon les
 Carrés magiques Clic ! Ma Classe
Carrés magiques Clic ! Ma Classe
Vous trouverez ci-dessous des fiches au format PDF pour les différents niveaux de difficulté Chacune propose 6 carrés magiques différents et leur corrigé
 [PDF] Fichier-CARRES-MAGIQUESpdf
[PDF] Fichier-CARRES-MAGIQUESpdf
CARRES MAGIQUES 1 2 3 4 5 6 7 8 9 10 11 CARRES MAGIQUES 1 12 12 12 12 Utilise les nombres : 12 01234 5678
 [PDF] Les Carrés Magiques
[PDF] Les Carrés Magiques
Fonctionnement du carré magique : Tu dois trouver le même nombre (la même somme) : -en additionnant les trois nombres qui sont sur chacune des lignes
 [PDF] Le carré magique - MAThenJEANS
[PDF] Le carré magique - MAThenJEANS
Sujet: Le but du carré magique 3x3 est de remplir un carré avec tous les chiffres de 1 à 9 Mais attention : chaque nombre ne doit apparaître qu'une seule
 Des ceintures de carrés magiques ou pas ! - apreslaclassenet
Des ceintures de carrés magiques ou pas ! - apreslaclassenet
11 avr 2018 · J'aime utiliser les carrés magiques en classe : c'est une façon de que vous pourrez compléter avec d'autres carrés magiques (ceux du
 [PDF] Laddition - Carrés magiques - Soutien 67
[PDF] Laddition - Carrés magiques - Soutien 67
L'addition Carrés magiques Un carré magique est un tableau dans lequel les sommes des lignes colonnes et diagonales principales sont égales
 CARRÉ MAGIQUE CP CE CM - PDF Free Download - DocPlayerfr
CARRÉ MAGIQUE CP CE CM - PDF Free Download - DocPlayerfr
Pour compléter ce super carré tu dois placer les nombres mystérieux qui manquent : ce super carré contient tous les nombres de à 5 et la somme des nombres dans
 Carrés Magiques année - PDF Téléchargement Gratuit - DocPlayerfr
Carrés Magiques année - PDF Téléchargement Gratuit - DocPlayerfr
Il nous reste à compléter en faisant des sommes égales à 15 On obtient le carré magique suivant : On remarque que les 8 carrés magiques s'obtiennent les
Comment compléter le carré magique ?
Le but du carré magique 3x3 est de remplir un carré avec tous les chiffres de 1 à 9. Mais attention : chaque nombre ne doit apparaître qu'une seule fois, et les sommes des chiffres de chaque ligne, de chaque colonne, et de chaque diagonale doivent être égales.Comment construire un carré magique 3x3 ?
Propriété Pour calculer la somme magique S d'un carré magique formé des nombres de 1 à n comportant n2 cases, on peut utiliser la formule : S = n(n2+1)2.
Club de mathématique 1
Les carrés magiques
Ce document contient trop de matière pour un seul club de mathématiques. La matière du début est plus simple (niveau milieu à fin primaire). Les choses se corsent peu à peu par la suite pour satisfaire lesélèves plus avancés.
Même les élèves du secondaire peuvent débuter avec la partie facile du début, elle prépare bien pour la suite.Première partie : pour les jeunes du primaire
(3e à 8e année) Un carré magique est un carré divisé en n rangées et n colonnes (donc n2 cases) dans lequel on met un nombre dans chaque case de manière à ce que la somme des n nombres de chaque rangée, de chaque colonne et de chaque diagonale est constante. On peut appeler cette constante la constante magique du carré. 2 7 6 9 5 1 4 3 8 est un carré magique 3 par 3, la constante magique est 15.16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
est un carré magique 4 par 4, la constante magique est 34 Un carré magique, comme les deux exemples qui précèdent, dans lequel les n2 nombrHV VRQP OHV QRPNUHV 1 2 3 " Q2, est appelé un carré normal.Instructions pour le professeur :
Les démarches suivantes expliquent la construction et la composition du carré 3 par 3. Pourquoi par exemple le 5 doit-ilêtre toujours au centre?
Il faut procéder lentement et laisser les enfants deviner des choses avant de tout écrire. Il faut les faire observer par eux- mêmes les différentes notions. Par exemple en regardant un un coin apparaît dans trois lignes distinctes (une rangée, une colonne et une diagonale). Puis, en regardant les huit combinaisons possibles de trois nombres de 1 à 9 dont la somme est 15, ils doivent observer combien de fois chaque nombre de 1 à 9 apparaît dans ces sommes. Par exemple le 4 apparaît trois fois (2 + 4 + 9 = 15, 3 + 4 + 8 = 15, 4 + 5 + 6 = 15). Ils doivent comprendre ce qui se passe et faire les déductions quiÉtude du carré 3 par 3.
(essayez avec les chiffres 1, 2, 3, 4). Le carré magique 3 par 3 est donc le nombres, soit 1, 2, 3, 4, 5, 6, 7, 8, 9.La somme de ces neuf nombres est :
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45.
Comme il y a trois rangées (ou trois colonnes), toutes égales et dont la somme est 45, la somme dans chaque rangée (et dans chaque colonne et diagonale) doit être égale à 45153. La constante magique du carré est donc
égale à 15.
Deuxièmement : on constate facilement que le carré doit contenir huit différentes sommes de trois entiers entre 1 et 9 (inclusivement) dont la somme est 15 : deux diagonales, trois lignes et trois colonnes. En observant plus attentivement on constate également ceci : le nombre au centre du carré apparaît dans quatre sommes distinctes (une ligne, une colonne et les deux diagonales) les nombres dans les coins apparaissent dans trois sommes distinctes (une ligne, une colonne et une diagonale) les nombres dans les milieux des lignes ou des colonnes du contour colonne) Nombre de sommes selon la position dans le carré : 3 2 3 2 4 2 3 2 3 Troisièmement, écrivons toutes les sommes de trois nombres distincts, entre 1 et 9 inclusivement, dont la somme est égale à 15. Avec un peu de patience, par essai et erreur, ou méthodiquement, peu importe, on trouve exactement 8 sommes possibles :1 + 5 + 9
1 + 6 + 8
2 + 4 + 9
2 + 5 + 8
2 + 6 + 7
3 + 4 + 8
3 + 5 + 7
4 + 5 + 6
En observant ces sommes on aperçoit que le 5 apparaît dans quatre sommes distinctes (1 + 5 + 9, 2 + 5 + 8, 3 + 5 + 7, 4 + 5 + 6). On aperçoit que les nombres pairs 2, 4, 6 et 8 apparaissent chacun dans trois sommes distinctes (par exemple pour 2 : 2 + 4 + 9, 2 + 5 + 8, 2 + 6 + 7) Finalement, on aperçoit que les nombres impairs 1, 3, 7 et 9 apparaissent exactement dans deux sommes distinctes (par exemple pour 1 : 1 + 5 + 9 et 1 + 6 + 8)Le 5 4 sommes
2, 4, 6 et 8 3 sommes
1, 3, 7 et 9 2 sommes
En mettant " deuxièmement » et " troisièmement » ensembles, que remarque-t-on?3 2 3 Le 5 4 sommes
2 4 2 2, 4, 6 et 8 3 sommes
3 2 3 1, 3, 7 et 9 2 sommes
seul qui intervient dans quatre sommes distinctes. On voit ensuite que les nombres pairs, 2, 4, 6 et 8, doivent être dans On voit finalement que les nombres impairs 1, 3, 7 et 9, doivent être dans les milieux des lignes du pourtour.Notre carré doit donc ressembler à ceci :
Pair Impair Pair
Impair 5 Impair
Pair Impair Pair
Finalement, construisons notre carré.
On commence avec un 5 au centre
5 placer automatiquement le 8 car la diagonale qui contient 2 et 5 doit contenir8 pour que ça fasse 15 en tout (2 + 5 + 8 = 15).
8 5 2 Ensuite on place le 4 dans un des coins restants, ce qui place automatiquement le 6 car 4 + 5 + 6 = 15. 685 24
Finalement les quatre cases restantes se remplissent automatiquement car la somme de chaque ligne et chaque colonne doit faire 15. On obtient le carré suivant : 6 1 8 7 5 3 294
Observations finales
Il y a huit sommes possibles de trois nombres distincts de 1 à 9 et le carré carré 3 par 3. dans un coin (quatre choix). Cela place automatiquement le 8 (on complète la diagonale 2 ± 5 ± 8) Ensuite on place le 4 dans un des coins restants (deux choix). Il y a donc 8 carrés 3 par 3 possibles (4 x 2 = 8)Ces carrés sont les suivants :
2 9 4 2 7 6 4 9 2 6 7 2
7 5 3 , 9 5 1 , 3 5 7 , 1 5 9 ,
6 1 8 4 3 8 8 1 6 8 3 4
4 3 8 6 1 8 8 3 4 8 1 6
9 5 1 , 7 5 3 , 1 5 9 3 5 7
2 7 6 2 9 4 6 7 2 4 9 2
et ou 270) ou par une réflexion (avec comme axe de symétrie la rangée centrale du carré, la colonne centrale du carré ou une des deux diagonales). On dit que ces huit carrés sont équivalents.Exemples :
2947 5 3 6 1 8 avec une rotation de 90 (sens horaire) devient le carré 6 7 2 1 5 9 8 3 4 6 7 2 1 5 9 8 3 4 avec la réflexion par rapport à la rangée centrale devient le carré 8 3 4 1 5 9 6 7 2
Exercices possibles :
1 Après avoir bien compris que le placement initial du 5, du 2 et du 4
Exemple : Le choix initial
245 conduit au carré 294
7 5 3 6 1 8
2. Prenez un carré initial donné et amusez-vous à faire les différentes
rotations3. Prenez un carré initial donné et amusez-vous à faire les différentes
réflexions4. Prenez un carré. Faites ses trois rotations (90, 180 et 270) dans le
sens horaire. Vous avez maintenant 4 carrés. Observez que les images miroir de ces carrés donnent quatre nouveaux carrés et vérifiez que chacun de ces nouveaux carrés peut être directement obtenu du carré initial par une des quatre réflexions. 2 7 6 9 5 1 4 3 8 est 6 7 2 1 5 9 8 3 45. Considérez les deux carrés magiques 4 par 4 suivants :
1 14 15 4 7 2 16 9
12 7 6 9 12 13 3 6
8 11 10 5 1 8 10 15
13 2 3 16 14 11 5 4
et par une rotation ou une réflexion, ce ne sont pas tous deux des images du même carré, ce sont deux carrés complètement différents). Cet exercice en a en fait beaucoup plus.Approfondissement possible, pour des groupes plus
avancésGénéralités sur les carrés 4 par 4
Après avoir étudié le carré 3 par 3 on peut parler des carrés 4 par 4. La situation est nettement plus complexe et on ne peut pas en faire une étude approfondie facilement, on peut cependant dire plusieurs choses intéressantes. Comme on a vu, il y a huit carrés magiques 3 par 3, mais ces carrés sont en faits équivalents et sont différentes angles. Bernard Frénicle de Bessy (France, 17e siècle) a fait une étude complète des carrés magiques normaux 4 par 4 (publiée à titre posthume en 1693). Dans cette étude il magiques 4 par 4 distinctes. Chacune de ses classes classé tous ces carrés magiques en fonction du placement des paires de nombres dont la somme est 17. carrés suivants :1 14 15 4 7 2 16 9
12 7 6 9 12 13 3 6
8 11 10 5 1 8 10 15
13 2 3 16 14 11 5 4
et Dans le premier, les deux nombres de chaque paire dont la somme est 17 sont placés symétriquement par rapport au centre du carré. Par exemple 1 et 16 ou encore 6 et 11. Dans le second, les deux membres de chaque paire sont 7. 10 . En fonction de ses placements, les carrés des diverses catégories ont les propriétés particulières, parfois très intéressante. Les carrés de la catégorie du second exemple sont très intéressants, on les appelle des carrés diaboliques. Parmi leurs propriétés, tous les sous carrés2 par 2 de ces carrés (chacun en a 9) contient quatre
nombres dont la somme est 34, la constante magique du carré.Construction de carrés 4 par 4.
haut en bas et de gauche à droite, les nombres de 1 à 16.1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
dans chaque diagonale pour obtenir le carré magique suivant :16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
précédent, on obtient le carré magique suivant :16 3 5 10
9 6 4 15
2 13 11 8
7 12 14 1
type que notre premier exemple : les paires de nombres dont la somme est égale à 17 sont placés symétriquement par rapport au centre du carré. Ces carrés sont dits symétriques. Notez que les trois carrésPropriétés des carrés 4 par 4
À priori dans un carré normal 4 par 4 nous avons 10 lignes dont la somme des quatre nombres est égale à 34 (quatre rangées, quatre colonnes et deux diagonales). En fait il y a toujours au moins quatre autres groupes de quatre nombres dont la somme est 34. Considérons le carré suivant : a c c a d b b d d b b d a c c aSi ce carré est magique et normal,
la somme des quatre nombres marqués " a » estégale à 34 (les 4 coins)
la somme des quatre nombres marqués " b » estégale à 34 (le carré central)
la somme des quatre nombres marqués " c » est égale à 34 (les nombres situés au milieu de la rangée du haut et de la rangée du bas) la somme des quatre nombres marqués " d » est égale à 34 (les nombres situés au milieu des colonnes de droite et de gauche). quatre sommes sont toujours égales à la constante magique du carré. Vous pouvez vérifier que ces sommes sont bien égales àPreuve de cette affirmation :
Appelons A la somme des quatre nombres marquées " a ». Appelons B la somme des quatre nombres marqués " b ». Appelons C la somme des quatre nombres marqués " c ». Appelons D la somme des quatre nombres marqués " d ». On voit clairement que A + B = 68 (deux diagonales). A + C = 68 (deux rangées). A + D = 68 (deux colonnes). B + C = 68 (deux colonnes). Puisque A + B = A + C = A + D, on a B = C = D. Puisque B + C = 68 et B = C, on a B = C = 34. A + C = 68 entraîne que A = 34. A + D =68 entraîne que D = 34.
On a bien montré que A = B = C = D = 34!
carré magique 4 par 4 en remplaçant 34 par la constante magique du carré. Donc, dans tout carré magique 4 par 4, il y a 14 groupes de 4 nombres dont la somme est égale à la densité du carré (quatre rangées, quatre colonnes, deux diagonales, les quatre coins, le carré central, les nombres au milieu des rangées du haut et du bas, les nombres au milieu des colonnes de gauche et de droite). de huit sommes de trois nombres donnant 15 et on a vu à 9 dont la somme est 15. Chacune des huit sommes doit être utilisées. Dans le cas du carré 4 par 4 la situation est bien différente. On a besoin de 14 groupes de quatre nombres de 1 à 16 dont la somme est 34, il en existe 86. Le choix est beaucoup plus grand et cela explique pourquoi il y a bien plus de carrés 4 par 4 que de carrés 3 par 3. Certains carrés ont bien plus que 14 groupes de quatre nombres, bien placés (ligne, carré, double SMLUH "B Mais puisque le choix se fait parmi 86 sommes possibles, les possibilités sont grandes. Outre les lignes (10 lignes), les carrée 2 par 2 (9 carrés) configurations sont possibles. En voici quelques-unes :X X X X X
X X X X X XX X X X X
X X XX X X X X
X X X X XX XX X X X X X X X Xquotesdbs_dbs16.pdfusesText_22[PDF] carré magique cm à imprimer
[PDF] exemple de texte argumentatif court
[PDF] définition du travail pdf
[PDF] qu est ce que le luxe
[PDF] kering
[PDF] le marché du luxe
[PDF] le luxe définition
[PDF] rousseau voyage
[PDF] texte de rousseau sur le voyage
[PDF] restaurant d'application le castel dijon
[PDF] site lycee castel dijon
[PDF] restaurant d'application le gustave dijon
[PDF] bts lycée castel dijon
[PDF] restaurant d'application dijon
