 SOLUTIONNAIRE : LOGICIELS STATISTIQUES EXERCICES
SOLUTIONNAIRE : LOGICIELS STATISTIQUES EXERCICES
Le test pour comparer les moyennes est le test de Student pour données avec variances Test d'égalité des espérances: deux observations de variances ...
 Chapitre 3 - Comparaison de plusieurs moyennes pour des
Chapitre 3 - Comparaison de plusieurs moyennes pour des
tests t − Student de comparaison de deux moyennes ... Remarque 11 : Le rejet de l'égalité des moyennes ne permet pas de savoir quelles sont les moyennes.
 Quelques tests de comparaison en paramétrique
Quelques tests de comparaison en paramétrique
tests de comparaisons d'une moyenne observée à une moyenne théorique ne nécessitent aucune ... ➢ On augmente le risque de rejeter H0 (égalité des moyennes entre.
 : tdr31p ————— Comparaisons de deux moyennes avec le test
: tdr31p ————— Comparaisons de deux moyennes avec le test
Cette fiche donne un exemple simple complet et reproductible d'un test de comparaison de deux moyennes avec le test t de Student.
 Tests paramétriques de comparaison de 2 moyennes
Tests paramétriques de comparaison de 2 moyennes
La variance comme la moyenne
 Global Strategy to Improve Agricultural and Rural Statistics
Global Strategy to Improve Agricultural and Rural Statistics
Pour cet exercice assurez-vous que l'utilitaire d'analyse (Toolpak) est activé dans Excel. • Nous commençons par le test d'égalité des espérances (T-test)
 Récapitulatif des conditions dapplication des tests de comparaison
Récapitulatif des conditions dapplication des tests de comparaison
: moyennes des observations des échantillons; S1 S2: estimations de l'écart Test F d'égalité des variances. Statistique T=f(S) suit loi de Student à n1+ ...
 Les tests statistiques dits ”non paramétrique”
Les tests statistiques dits ”non paramétrique”
qui n'est autre que le test de comparaison de moyennes de Student). • L'équivalent utilise l'équivalent paramétrique de ce test (l'égalité des variances étant.
 Comparaison de moyennes Tests visant à mettre en évidence une
Comparaison de moyennes Tests visant à mettre en évidence une
7 oct. 2020 ... égalité des moyennes par le test de Student d`es que l'intervalle de confiance `a 95% sur la différence entre les 2 moyennes ne contient pas ...
 Test de comparaison de deux proportions
Test de comparaison de deux proportions
Cet article est la suite de l'article Tests statistiques avec une calculatrice ou Geogebra dans lequel nous avions abordé les tests de conformité d'une
 SOLUTIONNAIRE : LOGICIELS STATISTIQUES EXERCICES
SOLUTIONNAIRE : LOGICIELS STATISTIQUES EXERCICES
La sortie EXCEL pour ce test est la suivante : Test d'égalité des espérances: observations pairées. Score. Norme. Moyenne. 773333333.
 STATISTIQUES IUT DEUXIEME PARTIE
STATISTIQUES IUT DEUXIEME PARTIE
Ce test est utilisé pour comparer deux moyennes de grandeurs de même nature et exprimées égalité à l'aide d'un test de Fisher-Snédécor (voir page 56).
 Récapitulatif des conditions dapplication des tests de comparaison
Récapitulatif des conditions dapplication des tests de comparaison
tests de comparaison de fréquences et de moyennes et des tests d'indépendance. Unité d'enseignement STA 109. CNAM. Chaire de Statistique Appliquée.
 Quelques tests de comparaison en paramétrique
Quelques tests de comparaison en paramétrique
est de petite taille (n ? 30) les tests de comparaisons d'une moyenne On augmente le risque de rejeter H0 (égalité des moyennes entre.
 Test de comparaison de deux proportions
Test de comparaison de deux proportions
Cet article est la suite de l'article Tests statistiques avec une calculatrice ou Geogebra dans lequel nous avions abordé les tests de conformité d'une
 Chapitre 3 - Comparaison de plusieurs moyennes pour des
Chapitre 3 - Comparaison de plusieurs moyennes pour des
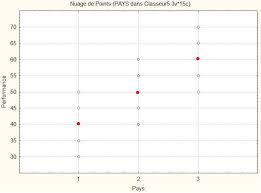
On fait passer le même test de logique (noté sur 100) aux trois échantillons d'élèves. – Population : élèves de troisième qui font leurs études dans trois pays
 Tests statistiques élémentaires
Tests statistiques élémentaires
Comparaison de ?1 et ?2. Il est utile de tester l'égalité de deux variances. H0 : ?1 = ?2 préalablement au test d'égalité des moyennes. La statistique.
 Cours 10 Test de comparaison de moyennes
Cours 10 Test de comparaison de moyennes
22-Nov-2011 Nombre de groupes à comparer? Critère paramétrique. Les postulats d'utilisation sont respectés. Tests paramétriques. Tests ...
 Tests de comparaisons proportions
Tests de comparaisons proportions
Tests de comparaisons proportions. Yohann.Foucher@univ-nantes.fr. Equipe d'Accueil 4275 "Biostatistique recherche clinique et mesures subjectives en.
 Chapitre 5 - Tests de comparaison de deux moyennes.
Chapitre 5 - Tests de comparaison de deux moyennes.
Dans ce cas on se ramène à un test de confor- mité de la moyenne des différences D = Y ? X à une valeur théorique (souvent 0). – soit les deux échantillons
 [PDF] COMPARAISON DE DEUX MOYENNES - R2MATH
[PDF] COMPARAISON DE DEUX MOYENNES - R2MATH
9 fév 2000 · On peut également tester leur égalité Quels cas sait-on traiter dans le cadre des tests paramétriques ? • Cas où les populations sont
 [PDF] Tests statistiques élémentaires
[PDF] Tests statistiques élémentaires
Comparaison de ?1 et ?2 Il est utile de tester l'égalité de deux variances H0 : ?1 = ?2 préalablement au test d'égalité des moyennes La statistique
 [PDF] Quelques tests de comparaison en paramétrique - Jonathan Lenoir
[PDF] Quelques tests de comparaison en paramétrique - Jonathan Lenoir
Comparaison de deux moyennes observées Quelques tests de comparaison en paramétrique 3 1 Échantillons indépendants 3 1 1 Les deux variances ne sont pas
 [PDF] Tests paramétriques de comparaison de 2 moyennes
[PDF] Tests paramétriques de comparaison de 2 moyennes
La variance comme la moyenne est un paramètre caractérisant la distribution d'une variable Distributions très différentes bien que les moyennes soient égales
 [PDF] STATISTIQUE : TESTS DHYPOTHESES
[PDF] STATISTIQUE : TESTS DHYPOTHESES
Les plus connus sont certainement les tests portant sur la moyenne la variance ou sur les proportions On connaît la loi théorique en général la loi normale
 [PDF] L2 - Trois exercices sur les tests paramétriques de comparaison
[PDF] L2 - Trois exercices sur les tests paramétriques de comparaison
Cette feuille d'exercices comporte en vérité quatre type d'exercices : comparaison de proportions comparaison d'écart- types comparaison de moyennes pour
 [PDF] Comparaison de deux moyennes
[PDF] Comparaison de deux moyennes
III- Comparaison de deux variances ? Test F de Snedecor Test Z (? ) ou de l'écart M : moyenne inconnue de la population d'où est issu l'échantillon
 [PDF] Analyse de la variance ANOVA
[PDF] Analyse de la variance ANOVA
Test d'égalité des k effets Comparaison de moyennes 1 Analyse de variance `a un facteur 2 Tests d'hypoth`eses Tableau d'analyse de variance
 [PDF] Tests de comparaison
[PDF] Tests de comparaison
Récapitulatif des conditions d'application des tests de comparaison de fréquences et de moyennes et des tests d'indépendance Unité d'enseignement STA 109
 [PDF] Comparaison des moyennes de deux populations normales décarts
[PDF] Comparaison des moyennes de deux populations normales décarts
On désire tester (sur échantillons) l'hypothèse d'égalité des moyennes : (H) : ' m1 - m 2 Il - PRINCIPE DU TEST Sous des réserves très larges - en ce
Quel test pour comparer des moyennes ?
L'ANOVA est un test statistique qui généralise le test t ? Student au cadre de comparaisons de plusieurs moyennes. On l'applique dès lors que l'on étudie les effets d'une ou plusieurs variables qua- litatives sur une variable quantitative.Quand utiliser le test z ?
On utilise :
1le test t de Student si on ne connaît pas la vraie variance des populations dont sont extraits les échantillons ;2le test z si on connaît la vraie variance ?² de la population.Comment choisir H0 et H1 ?
Les formulations pour l'hypoth`ese alternative H1 sont : 1. H0 : µ = ? (ou µ ? ?) et 2. H0 : µ = ? (ou µ ? ?) H1 : µ<? H1 : µ>? (unilatéral `a gauche). (unilatéral `a droite).Déroulement du test :
1on calcule la moyenne observée : ¯x=x1+?+xnn. 2on calcule l'écart-type débiaisé : s2=(x1?¯x)2+?+(xn?¯x)2n?1. 3on calcule l'écart du test : t=¯x?m0s×?n. 4on cherche l'écart critique ta dans la table de la loi de Student avec n?1 degrés de liberté.
Quelques tests de
comparaison en paramétrique Jonathan Lenoir (MCU), jonathan.lenoir@u-picardie.fr http://www.u-picardie.fr/edysan/Plan du cours
1. Comparaison entre moyennes observée et théorique
1.1. Grands échantillons (n > 30)
1.2. Petits échantillons (n 30) et distribution Normale
2. Comparaison de deux variances observées
3. Comparaison de deux moyennes observées
Quelques tests de comparaison en paramétrique
3.1. Échantillons indépendants
3.1.1. Les deux variances ne sont pas différentes
3.1.2. Les deux variances sont différentes
3.2. Échantillons appariés
4. Comparaison de plus de deux moyennes observées
Plan du cours
1. Comparaison entre moyennes observée et théorique
1.1. Grands échantillons (n > 30)
1.2. Petits échantillons (n 30) et distribution Normale
2. Comparaison de deux variances observées
3. Comparaison de deux moyennes observées
Quelques tests de comparaison en paramétrique
3.1. Échantillons indépendants
3.1.1. Les deux variances ne sont pas différentes
3.1.2. Les deux variances sont différentes
3.2. Échantillons appariés
4. Comparaison de plus de deux moyennes observées
Moyenne observée vs. Moyenne théorique
de confiance, on distingue deux cas : ¾grand (n> 30) et la distribution des valeurs pour la Dans ce cas on fait une approximation par la loi Normale car on sait désormais que la distribution de la moyenne tend vers une loiNormale (cf. chapitre 2) : test U-Normale (LNCR)
¾(n30) et la distribution des valeurs pour la
variable est proche dune loi Normale Dans ce cas on fait une approximation par les lois de Student afin de moyenne pour les petits échantillon (cf. chapitre 2) : test t-Student NB : Dans le doûte, optez toujours pour un test t-Student car les lois de Student tendent vers la loi Normale pour les grands (n> 30) échantillonsConditions requises
est de petite taille (n observée à une moyenne théorique ne nécessitent aucune autre conditionet sont donc peu restrictifsLe choix de H0 et H1
Comme dans les exemples évoqués au chapitre 3, le critère fonction des observations est la moyenne mde la variable Yet on veux en général démontrer que mest soit différente, inférieure ou bien supérieure à une valeur théorique 0:¾H0 :
¾H1 :
Cas bilatéral :
Cas unilatéral droit :
Cas unilatéral gauche :
Plan du cours
1. Comparaison entre moyennes observée et théorique
1.1. Grands échantillons (n > 30)
1.2. Petits échantillons (n 30) et distribution Normale
2. Comparaison de deux variances observées
3. Comparaison de deux moyennes observées
Quelques tests de comparaison en paramétrique
3.1. Échantillons indépendants
3.1.1. Les deux variances ne sont pas différentes
3.1.2. Les deux variances sont différentes
3.2. Échantillons appariés
4. Comparaison de plus de deux moyennes observées
n> 30) La moyenne mcalculée sur un grand échantillon de taille nsuivra une loi approximativement Normale : Comme déjà vu, dans ce cas, on commet une erreur négligeable en remplaçant la valeur 2(inconnue en général) par son estimation calculée sur l'échantillon :1RXNOLH] SMV TXH OHŃMUP
type de la moyenne deO˔ŃOMQPLOORQ VH ŃMOŃXO ˋ
OMLGH GH OM IRUPXOH GH
OHUUHXU VPMQGMUG
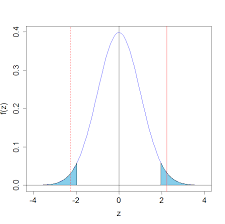
H1 bilatérale
choisi et un test bilatéral (H1 : m0), on calcul :Et on rejette H0 si :
/2/2Ucrit-Ucrit Voir table des fractiles de la loiNormale
H1 unilatérale
Et on rejette H0 si :
choisi et un test unilatéral droit ou gauche (H1 : m>0 ou m< 0), on calcul :¾Cas unilatéral droit (H1 : m> 0) :
Ucrit¾Cas unilatéral gauche (H1 : m< 0) :
-Ucrit Voir table des fractiles de la loiNormale
Exercice
> FM <-c(180, 165, 175, 182, 177, 180, 184, 205, 206, 200,191, 193, 201, 182, 177, 184, 193, 185, 199, 203, 200, 195,
206, 207, 185, 204, 199, 198, 180, 177, 175, 180)
Prunus avium
Soit la longueur (mm) de 32 feuilles
1.La longueur moyenne des feuilles de Merisier
est supposée être de 185 mm, peut-on dire que la longueur moyenne des feuilles issues de ce de 5% ?2.Calculez la probabilité Pexacte de votre test
3. -ci posez
H1 unilatérale droite
Solutions
1. Calcul de Uobs:
> Uobs <-(mean(FM)-185)/(sd(FM)/sqrt(length(FM))) > Uobs [1] 2.2451861. Calcul de Ucrit:
> Ucrit <-qnorm(1-(0.05/2)) > Ucrit [1] 1.9599641. Comparaison de Uobset Ucrit:
> Uobs>Ucrit [1] TRUE1. Verdict et conclusion ?
2. Calcul de la probabilité P
Solutions
> 1-pnorm(Uobs)+pnorm(-Uobs) [1] 0.0247562 $PPHQPLRQ QRXNOLH] pas que vous êtes en bilatéral !!! Il faut donc rajouter la probabilitéGRNVHUYHU
également ce
résultatSolutions
3. Calcul de Ucrit:
> Ucrit <-qnorm(1-(0.05)) > Ucrit [1] 1.6448543. Comparaison de Uobset Ucrit:
> Uobs>Ucrit [1] TRUE3. Calcul de la probabilité Psolution :
> 1-pnorm(Uobs) [1] 0.0123781 > chooseCRANmirror() > install.packages("TeachingDemos") > library(TeachingDemos) > z.test(FM, mu=185, stdev=sd(FM), alternative=c("two.sided"))One Sample z-test
data: FM z = 2.2452, n = 32.000, Std. Dev. = 11.653, Std. Dev. of the sample mean = 2.060, p-value = 0.02476 alternative hypothesis: true mean is not equal to 18595 percent confidence interval:
185.5875 193.6625
sample estimates: mean of FM189.625
Installez le module et utilisez la fonction
Les joies de R
Calculez votre
intervalle de confiance à 95% et vérifiez le résultat > z.test(FM, mu=185, stdev=sd(FM), alternative=c("greater"))One Sample z-test
data: FM z = 2.2452, n = 32.000, Std. Dev. = 11.653, Std. Dev. of the sample mean = 2.060, p-value = 0.01238 alternative hypothesis: true mean is greater than 18595 percent confidence interval:
186.2367 Inf
sample estimates: mean of FM189.625
Utilisez à nouveau la fonction
unilatérale droite cette fois :Les joies de R
> t.test(FM, mu=185, alternative=c("two.sided"))One Sample t-test
data: FM t = 2.2452, df= 31, p-value = 0.03203 alternative hypothesis: true mean is not equal to 18595 percent confidence interval:
185.4237 193.8263
sample estimates: mean of x189.625
Utilisez maintenantla fonction
-vous ?Les joies de R
Calculez votre
intervalle de confiance à 95% et vérifiez le résultatPlan du cours
1. Comparaison entre moyennes observée et théorique
1.1. Grands échantillons (n > 30)
1.2. Petits échantillons (n 30) et distribution Normale
2. Comparaison de deux variances observées
3. Comparaison de deux moyennes observées
Quelques tests de comparaison en paramétrique
3.1. Échantillons indépendants
3.1.1. Les deux variances ne sont pas différentes
3.1.2. Les deux variances sont différentes
3.2. Échantillons appariés
4. Comparaison de plus de deux moyennes observées
Les lois de Student
Comme déjà vu, pour un petit échantillon de taille n 30 dont la distribution de la variable étudiée est proche de la loi Normale ou bien symétrique alors la moyenne msuivra une loi de Student à n-1degrés de liberté : Ensuite, la procédure est exactement la même que pour le test de la loi tde Student à n-1 degrés la loi NormaleH1 bilatérale
choisi, n-1 degrés de liberté et un test bilatéral (H1 : m0), on calcul :Et on rejette H0 si :
/2/2tcrit-tcrit Voir table du t deStudent
H1 unilatérale
Et on rejette H0 si :
choisi, n-1 degrés de liberté et un test unilatéral droit ou gauche (H1 : m>0 ou m< 0), on calcul :¾Cas unilatéral droit (H1 : m> 0) :
tcrit¾Cas unilatéral gauche (H1 : m< 0) :
tcrit Voir table du t deStudent
Exercice
> Cu <-c(1.352, 1.348, 1.349, 1.346, 1.354, 1.351, 1.355,1.354, 1.349, 1.350, 1.352, 1.351)
Le dosage du cuivre (Cu) par absorption atomique dans un sol de référence contenant 1,356 mg de cuivre par kg de sol sec a donné les résultats suivants ?1.Peut-on mettre en évidence, de 5%,un biais de
la méthode de dosage du cuivre connaissant la valeur de référence ?2.Calculez la probabilité Pexacte de votre test
Plan du cours
1. Comparaison entre moyennes observée et théorique
1.1. Grands échantillons (n > 30)
1.2. Petits échantillons (n 30) et distribution Normale
2. Comparaison de deux variances observées
3. Comparaison de deux moyennes observées
Quelques tests de comparaison en paramétrique
3.1. Échantillons indépendants
3.1.1. Les deux variances ne sont pas différentes
3.1.2. Les deux variances sont différentes
3.2. Échantillons appariés
4. Comparaison de plus de deux moyennes observées
Pourquoi comparer deux variances ?
Le test F-Fisher de comparaison de deux variances observées ¾Vérifier la condition de non différence des variances entre deux échantillons encore appelée homoscédasticité(cf. test t-Student de comparaison de deux moyennes observées)¾Fde Fisherest de comparer le rapport des deux
variances, qui est supposé égal à 1 sous H0, avec la loi de FisherRonald Fisher
(1890-1962)Conditions requises
Attention, ce test de comparaison de variances entre deux échantillons ¾Les 2 échantillons sont de taille suffisante (n1>30 et n2> 30) ¾Au moins un des 2 échantillons est de petite taille (n130 ou n230) mais la distribution de la variable étudiée suit une loi Normale au sein de NB : le test Fde comparaison de deux variances est très ormalité et il est également peu puissant Si ces deux conditions ne sont pas respectés, il faudra opter pour une approche non paramétrique :¾Le test de Fligner-Killeen
pouvoir comparer des variances pour plus de deux échantillons tandis que le test F entre deux échantillons seulementLe choix de H0 et H1
Cette fois-ci, le critère fonction des observations est le rapport des variances estimées pour les deux échantillons de taille n1et n2dont on¾H0 :
¾H1 :
Cas unilatéral droit :
Cas bilatéral : ොߪ
En général, le
test F de Fisher est utilisé de manière bila´téraleH1 bilatérale
choisi, n1-1 et n2-1 degrés de liberté et un test bilatéral, on calcul :Attention, la loi
GH )LVOHU QHVP
pas symétrique etFcritINF-FcritSUP
Et on rejette H0 si :
/2FcritSUP
/2FcritINF
Astuce
À noter que :
Équivaut à :
Par conséquent, on calcul en pratique le rapport Fobsen faisant en sorte de calculer le rapport de la variance la plus grande (numérateur) sur la variance la plus petite (dénominateur) et on rejette H0 si :Fcrit/2
Voir table du FdeFisher
Table Fde Fisher
de 5%, on croise les degrés de liberté du numérateur et du dénominateur pour trouver la valeur du Fcritique noté Fcrit:Exercice
> F <-c(31, 25, 29, 30, 31, 28, 31, 29, 29, 33, 30, 28) > M <-c(28, 29, 30, 29, 27, 26, 27, 28, 25, 28) On dispose de deux échantillons (mâles vs. femelles) de Souris des Cactus (Peromyscuseremicus), dont on a mesuré le poids (g) chez adulte :1.Peut-on déceler, avec un
de 5%, une différence de la variance du entre mâles et femelles ?2.Calculez la probabilité P
exacte de votre test1. Calcul de Fcrit:
> Fcrit <-qf(1-(0.05/2), df1=11, df=9) > Fcrit [1] 3.9120741. Comparaison de Fobset Fcrit:
> Fobs>Fcrit [1] FALSE1. Verdict et conclusion ?
Solutions
1. Calcul de Fobs:
> c(var(F), var(M)) [1] 4.090909 2.233333 > Fobs <-var(F)/var(M) > Fobs [1] 1.83175Solutions
2. Calcul de la probabilité P
> 1-pf(Fobs, df1=11, df2=9)+pf(var(M)/var(F), df1=9, df2=11) [1] 0.3726192 $PPHQPLRQ QRXNOLH] pas que vous êtes en bilatéral !!! Il faut donc rajouter la probabilitéGRNVHUYHU
également ce
résultat > var.test(F, M, alternative=c("two.sided"))F test to compare two variances
data: F and M F = 1.8318, numdf= 11, denomdf= 9, p-value = 0.3726 alternative hypothesis: true ratio of variances is not equal to 195 percent confidence interval:
0.4682299 6.5721346
sample estimates: ratio of variances1.83175
Utilisez la fonction Fde
comparaison de variance entre vos deux échantillons :Les joies de R
> fligner.test(list(F, M))Fligner-Killeen test of homogeneity of variances
data: list(F, M) Fligner-Killeen:medchi-squared = 0.454, df= 1, p-value =0.5004
Utilisez la fonction une version non
paramétrique de comparaison de variance entre deux échantillons :Les joies de R
Plan du cours
1. Comparaison entre moyennes observée et théorique
1.1. Grands échantillons (n > 30)
1.2. Petits échantillons (n 30) et distribution Normale
2. Comparaison de deux variances observées
3. Comparaison de deux moyennes observées
Quelques tests de comparaison en paramétrique
3.1. Échantillons indépendants
3.1.1. Les deux variances ne sont pas différentes
3.1.2. Les deux variances sont différentes
3.2. Échantillons appariés
4. Comparaison de plus de deux moyennes observées
Échantillons indépendants ou appariés ?
Il est important de pouvoir bien distinguer ces deux cas et en général on repère trés rapidement les données appariées car les deux échantillons sont de la même taille et la variable est mesurée : ¾Deux fois de suite par le même opérateur dans des conditions différentes ¾Par deux opérateurs différents dans les mêmes conditions de traitement (effet observateur)¾À deux instants différents t1et t2
cours du temps (effet temporel) ¾Dans deux endroits différents (x1, y1) et (x2, y2) (effet spatial)¾Etc.
Plan du cours
1. Comparaison entre moyennes observée et théorique
1.1. Grands échantillons (n > 30)
1.2. Petits échantillons (n 30) et distribution Normale
2. Comparaison de deux variances observées
3. Comparaison de deux moyennes observées
Quelques tests de comparaison en paramétrique
3.1. Échantillons indépendants
3.1.1. Les deux variances ne sont pas différentes
3.1.2. Les deux variances sont différentes
3.2. Échantillons appariés
4. Comparaison de plus de deux moyennes observées
Conditions requises
Attention, il existe trois conditions à vérifier avant de réaliser ce test de comparaison de moyennes entre deux échantillons indépendants :¾Indépendancedes deux échantillons
¾Homoscédasticité(non différence des variances) ;condition dont on si les taille des échantillonssont voisines (n1n2) Si au moins un des deux échantillons est trop petit (n130 ou n230)quotesdbs_dbs35.pdfusesText_40[PDF] ecart type moyen excel
[PDF] ecart type excel definition
[PDF] écart type pondéré
[PDF] ecart type excel anglais
[PDF] formule de l'écart type
[PDF] écart type faible ou fort
[PDF] plus l'écart type est grand
[PDF] open office calc formule pourcentage
[PDF] ecart type libreoffice calc
[PDF] formules libreoffice calc
[PDF] calc fonction si plusieurs conditions
[PDF] fonction classeur open office
[PDF] open office calcul automatique
[PDF] calculer variance probabilité
