 exercices corrigés sur letude des fonctions
exercices corrigés sur letude des fonctions
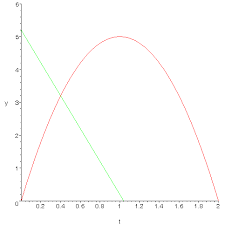
On désigne par g la fonction numérique définie sur [0 ; ]π par ( ) cos sin. g x x x x. = - . a. Etudier les variations de g et dresser son tableau de
 Série dexercices no2 Les fonctions Exercice 1 : images et
Série dexercices no2 Les fonctions Exercice 1 : images et
1. Calculer le domaine de définition des fonctions f définies de la façon suivante : a. f(x) = 5x + 4.
 de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n˚1
de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n˚1
Calculer la fonction dérivée de f et étudier son signe. 5. Dresser le tableau de variations de f. 6. Tracer (Cf ). Corrigé.
 Pascal Lainé Intégrales généralisées. Suites et séries numériques
Pascal Lainé Intégrales généralisées. Suites et séries numériques
Suites et séries numériques. Suites et séries de fonctions. Séries entières. Exercices corrigés. Licence STS. L2 Mathématiques et Économie. Université Lyon 1.
 Analyse Numérique
Analyse Numérique
fonction spline. D'un point de vue numérique cette idée est très bonne ... Exercices du chapitre 7. Exercice 7.1 Que se passe-t-il dans la méthode de la ...
 1sex Exercices avec solutions FONCTIONS - Généralités PROF
1sex Exercices avec solutions FONCTIONS - Généralités PROF
Exercice 15 : Soit f la fonction numérique tel que: ( ). (. )( ) 2. 3 1 2. 4. 1 x x. f x x. +. -. = -. Etudier le signe de le fonction f. Solution : 2. 4. 1 0 x
 TRAVAUX DIRIGÉS N°1 - MATHÉMATIQUES
TRAVAUX DIRIGÉS N°1 - MATHÉMATIQUES
Calculer les dérivées partielles du premier et du second ordre des fonctions numériques Exercice 2 Optimisation sans contrainte d'une fonction de deux ...
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
numérique. 1479. 327 453.00 Méthode de Newton. 1479. 328 454.00 Résolution d ... fonction xex sur R. 14. L'ensemble des nombres complexes d'argument π/4+kπ ...
 Séries de fonctions
Séries de fonctions
Correction exercice 2. 1. On va appliquer les règles de Riemann avec. ( ). (. ) Donc la série (numérique)
 Corrigé du TD no 9
Corrigé du TD no 9
Par un raisonnement semblable à celui de l'exercice précédent on en déduit que la fonction x ↦→ cos. (1 x. ) n'admet pas de limite en 0. Exercice 8 a) D
 Généralités sur les fonctions numériques dune variable réelle
Généralités sur les fonctions numériques dune variable réelle
Fonctions de plusieurs variables a) Dérivées partielles et différentielles b) Calcul incertitude. 3. Exercices corrigés. Cours 1
 exercices corrigés sur letude des fonctions
exercices corrigés sur letude des fonctions
Exercices corrigés Fonctions. Exercices corrigés. Fonctions. 1. Généralités Soit ? la fonction numérique de la variable réelle x telle que : ?.
 Série dexercices no2 Les fonctions Exercice 1 : images et
Série dexercices no2 Les fonctions Exercice 1 : images et
On considère la fonction f : x 7! x2 + 2x 3. Après avoir déterminé son ensemble de définition montrer que la courbe représentative Cf de f possède un axe de
 de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n?1
de la 1`ere S `a la TS. Chapitre 4 : Études de fonctions Exercice n?1
Calculer la fonction dérivée de f et étudier son signe. 4. Dresser le tableau de variations de f. 5. Tracer la courbe représentative de f. Corrigé. Exercice
 Cours danalyse 1 Licence 1er semestre
Cours danalyse 1 Licence 1er semestre
4.2 Propriétés de la limite d'une fonction . 7 Corrigé des exercices ... valeur approchée (utilisée dans le calcul numérique) d'un nombre réel ...
 MATH Tle D OK 2
MATH Tle D OK 2
si ? 0; sont les mêmes que celles sur les limites des fonctions numériques. f) Limites des suites définies à l'aide d'une fonction.
 L2 - Math4 Exercices corrigés sur les séries numériques
L2 - Math4 Exercices corrigés sur les séries numériques
Montrer par comparaison avec une intégrale
 Mathématiques pour léconomie et la gestion
Mathématiques pour léconomie et la gestion
Cours et exercices corrigés – L3 & Master 224 pages. Bruno AEBISCHER
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
A ?A = X. [000133]. Exercice 34. 1. Écrire l'ensemble de définition de chacune des fonctions numériques suivantes : x ??. ?x x. ?? 1 x?1.
 Séries numériques
Séries numériques
Déterminer en fonction du paramètre la nature de la série de terme général. ( ). Allez à : Correction exercice 8. Exercice 9. Etudier la nature de la série
 Les fonctions numériques tronc commun exercices corrigés
Les fonctions numériques tronc commun exercices corrigés
Propositions de corrigés pour les exercices concernant les fonctions numériques et la proportionnalité 1°) Exercice 1 1°) Méthode algébrique a) Soit dC la distance parcourue par le cyclise en km : dC = 30 × (t+15) = 30t + 45 (car la vitesse du cycliste vaut 30 km/h et la durée du parcours du cycliste (t+15) heures)
 Généralités sur les fonctions numériques - mathoxnet
Généralités sur les fonctions numériques - mathoxnet
Une fonction impaire a sa représentation graphique symétrique par rapport au centre du repère 1 2 Fonctions de référence 1 2 1 Fonctions affines Définition-Propriété : Soit a et b deux réels La fonction x ax+b définie sur ? est appelé une fonction affine La représentation graphique d'une telle fonction est une droite d d
Exercice 1
Soit ƒ la fonction définie sur ? par : ƒ(x) = x4 ? 4?x?. 1. Montrer que ƒ est paire. 2. a) Montrer que : ƒ(a)?ƒ(b)/a?b = (a + b)(a2 + b2)? 4 où a, b ? ?+ et a ? b. b) Déduire que ƒ est strictement décroissante sur [0, 1] et qu’elle est strictement croissante sur [1, +?[. 3. a) Dresser le tableau de variations de ƒ sur ?. b) Montrer que : (?x ? ?*) ...
Devoir surveillé Sur Les Fonctions numériques 1 Bac
Exercice 1 Soit ƒ la fonction définie par : ƒ(x) = ?x+7 ? ?x+3 1. Déterminer Dƒ. 2. 2.1. Montrer que ƒ est minorée par 0. 2.2. 0est-il un minimum de ƒ ? justifier votre réponse. 3. 3.1. Montrer que ƒ est majorée par2. 3.2. 2est-il un maximum de ƒ ? justifier votre réponse. 4. Montrer que ƒ est strictement décroissante sur Dƒ.
Comment calculer la fonction numérique ?
On considère la fonction numérique ƒ définie par : { ƒ(x) = 2x ? 3, si x? ]??, ?2[ et ƒ(x) = x3? 2x , si x? [?2, 2] et ƒ(x) = 2x + 3, si x? ]2, +?[ Déterminer Dƒ. Montrer que la fonction ƒ est impaire. Exercice 4 On considère le tableau de variations de la fonction ƒ définie ci-dessous. Déterminer Dƒl’ensemble de définition de ƒ.
Comment réussir le corrigé des différents exercices sur les fonctions?
Le corrigé des différents exercices sur les fonctions propose des rappels de cours pour montrer que l’assimilation des outils de base relatifs aux limites, comportement asymptotique, dérivation et continuité est importante pour aborder les différents thèmes de ce chapitre et réussir l’examen du bac.
Qu'est-ce que les fonctions numériques ?
Nous allons étudier quelques fonctions numériques (ayant pour arguments des nombres). Cellesci sont des fonctions de l'arithmétique générique. Leurs arguments peuvent être soit des entiers, soit des rationnels, soit des réels. Le type du résultat dépend du type des arguments. Il est réel si l'un des arguments est réel.
Quels sont les exercices corrigés sur les fonctions dérivées ?
Terminale – Exercices corrigés sur les fonctions dérivées – Terminale Justifier, dans chaque cas, que f est dérivable sur ? puis calculer On pose. Répondre aux questions suivantes pour chacune des fonctions ci-dessus. Déterminer la limite pour. Ces fonctions sont-elles toutes continues en ? Trouver les dérivées de ces fonctions.
BURKINA FASO
Unité - Progrès - Justice
MINISTERE
DE L'EDUCATION NATIONALE,
DEL'ALPHABETISATION ET DE LA PROMOTION
DESLANGUES NATIONALES
ANNALES
MATHÉMATIQUES
TERMINALE D
2AUTEURS :
Dieudonné KOURAOGO IES
Victor T. BARRY IESJean Marc TIENDREBEOGO IES
Clément TRAORE IESBakary COMPAORE IES
Abdou KABORE CPES
Maquette et mise en page :
OUEDRAOGO Joseph
ISBN :
Tous droits réservés :
© Ministre de l'Éducation Nationale, de l'AlphabétisationEt de la Promotion des Langues nationales
Edition :
Direction Générale de la Recherche en Éducation et de l'Innovation Pédagogique 3 4AVANT-PROPOS
La présente annale destinée à la classe de terminale D a pour but d'aider le professeur dans
son enseignement et le candidat au baccalauréat D de se préparer à l'épreuve de
mathématiques.Cette annale comporte trois parties :
Première partie : résumé du cours par chapitre Deuxième partie : énoncés des épreuves du baccalauréat D Troisième partie : propositions de corrigés des épreuves. Les candidats ne tireront profit qu'en résolvant et trouvant par eux-mêmes les solutions sansavoir recours aux corrigés. Les corrigés sont pour confirmer leurs justes réponses ou donner
d'autres pistes de résolution qui ne sont peut-être pas les leurs. Le succès résulte de l'effort et
de la méthode. Nous vous souhaitons du plaisir dans vos activités mathématiques et attendons vos critiques et suggestions pour des améliorations futures d'autres oeuvres.Les auteurs
5 6RAPPEL DE COURS
7Chapitre : Les suites numériques
Objectifs :
· Mettre en oeuvre les énoncés admis sur les limites des suites ; · Connaître les limites et les comportements asymptotiques comparés des suites numériques.1. Généralités sur les suites numériques
a) DéfinitionOn appelle suite numérique, toute application
définie de ℕ (ou d'un sous ensemble de ℕ) vers ℝ. On la note ()∈ℕ (ou ()∈). b) Modes de détermination d'une suiteUne suite numérique peut être définie :
Soit par une formule explicite qui permet de calculer les termes en fonction de .Exemples :
- Soit ()∈ℕ la suite définie par = 2 - 3. - Soit ()∈ℕ ∗ la suite définie par = Soit par la donnée d'un terme quelconque (en général son 1er terme) et d'une relation qui lie deux termes consécutifs (permettant de calculer un terme à partir du terme qui le précède).Exemples :
- Soit ()∈ℕ la suite définie par = 3 - Soit ()∈ℕ ∗ la suite définie par = 4 + 5 , c) Sens de variation d'une suite Soit ()∈ℕ une suite numérique.· Si pour tout
(resp. strictement croissante).· Si pour tout
décroissante (resp. strictement décroissante).· Si pour tout
∈ ℕ, = alors la suite ()∈ℕ est dite constante. d) Comparaisons sur les suitesSoient
()∈ℕ et ()∈ℕ deux suites numériques et 8 Si pour tout , ≥ (resp. > ) on dit que la suite () est supérieure () (resp. () est strictement supérieure à ()). Si pour tout () (resp. () est strictement inférieure à ()). On dit que la suite () est majorée s'il existe un réel ' tel que pour tout On dit que la suite () est minorée s'il existe un réel ( tel que pour tout Si la suite () est la fois minorée et majorée, on dit qu'elle bornée. Remarque : Une suite positive (resp. négative) est minorée par 0 (resp. majorée par 0).2. Suites arithmétiques et suites géométriques
a) Suites arithmétiques· Une suite
()∈ℕ est dite arithmétique s'il existe un réel ) tel que toutLe réel
) s'appelle la raison de la suite ()∈ℕ.· Soit
()∈ℕ est une suite arithmétique de raison ) et de 1er terme . On a : Si le 1er terme est alors pour tout - 1)). Pour tous entier et , (· Soit
()∈ℕ est une suite arithmétique de raison ). Si ) > 0 alors la suite () est croissante. Si ) < 0 alors la suite () est décroissante. Si ) = 0 alors la suite () est constante.· Soit
()∈ℕ est une suite arithmétique de raison ) et de 1er terme . La somme / des1er termes est : /= + + + ⋯+ .
2. Si le 1er terme est alors la somme / des1er termes est :
2. Si le 1er terme est - alors la somme / des ( + 1) 1er termes est : + 1) ×(-+ -) 2. 9 b) Suites géométriques· Une suite
()∈ℕ est dite géométrique s'il existe un réel 2 tel que tout = 2.Le réel
2 s'appelle la raison de la suite ()∈ℕ.
· Soit
()∈ℕ est une suite arithmétique de raison ) et de 1er terme . On a : = 2. Si le 1er terme est alors pour tout = 2(). Pour tous entier et , ( = -2(-).· Soit
()∈ℕ est une suite arithmétique de raison ). Si 2 > 1 alors la suite () est croissante. Si 0 < 2 < 1 alors la suite () est décroissante. Si 2 = 1 alors la suite () est constante. Si 2 < 0, () est une suite alternée· Soit
()∈ℕ est une suite arithmétique de raison 2 et de 1er terme . La somme / des1er termes est : /= + + + ⋯+ .
/= ×1 - 21 - 2.
Si le 1er terme est alors la somme / des1er termes est :
/= ×1 - 21 - 2.
Si le 1er terme est - alors la somme / des ( + 1) 1er termes est : /= -×1 - 21 - 2.
3. Convergence des suites numériques
a) Définition Soit ()∈ℕ une suite numérique. On dit que la suite () est convergent si elle admet une limite finie 3. On note lim→8= 3. On dit que la suite () est divergente si elle n'est pas convergente. On a lim→8= +∞ ou lim→8= -∞. b) Limite par comparaison Soit ()∈ℕ une suite numérique et S'il existe une suite () telle que pour tout , ≥ et lim→8= +∞ alors lim→8= +∞. 10 S'il existe un suite (:) telle que pour tout alors lim→8= -∞. S'il existe un réel 3 tel que pour tout lim→8:= lim→8= 3, alors lim→8= 3. Si pour tout Si pour tout c) Limite des suites monotones Soit ()∈ℕ une suite numérique. Si () est croissante et majorée alors () converge. Si () est décroissante et minorée alors () converge. Si () est monotone et bornée alors () converge. d) Convergence des suites arithmétiques et géométriques· Convergence des suites arithmétiques
Soit ()∈ℕ est une suite arithmétique de raison ) et de 1er terme . Si ) = 0 alors la suite () est convergente et lim→8= . Si ) ≠ 0 alors la suite () est divergente et lim→8= +∞, ) > 0 lim →8= -∞, >? ) < 0· Convergence des suites géométriques
Soit ()∈ℕ est une suite arithmétique de raison ) et de 1er terme . Si 2 = 1 alors la suite () est convergente et lim→8= Si |2| < 1 alors la suite () est convergente et lim→8= 0. Si 2 > 1 alors la suite () est divergente et lim→8= +∞, > 0 lim →8= -∞, >? < 0 e) Opérations sur les limites des suites Soit ()∈ℕ et ()∈ℕ deux suites numériques. Les propriétés sur les limites de la somme ( + ), du produit (× ) et du quotient @A BA), si ≠ 0; sont les mêmes que celles sur les limites des fonctions numériques. f) Limites des suites définies à l'aide d'une fonction· Suite de type
= C( Soit C une fonction définie sur ℝ et () une suite définie par = C( Si C admet une limite en +∞ alors lim→8= limD→8C(E).· Suite de type
= C() Soit C une fonction continue sur un intervalle de ℝ et () une suite numérique définie par = C().Si la suite
() est convergente et de limite 3, alors 3 = C(3). 11Chapitre : Courbes paramétrées
Objectifs :
· mettre en évidence et exploiter les périodicités et les symétries éventuelles, · dresser le tableau de variations des fonctions coordonnées x et y, · calculer les coordonnées (x'(t), y'(t)) du vecteur dérivé, · connaître l'interprétation cinématique du vecteur dérivé.1. Notion de courbes paramétrées
a) Définition Le plan est rapporté à un repère orthonormal (O,F,GHIH) et I est un intervalle de ℝ. SoitE et J deux fonctions de la variable réelle K.
A tout réel
K, on associe le point '(K) définie par le vecteurL'GGGGGGH(K)= E(K)FH+ J(K)IH.
L'ensemble (
M) des points '( E;J) du plan tels que :
OE = E(K)
J = J(K), K ∈ est appelée courbe paramétrée de paramètre K.On note
'(K) ( E(K);J(K)) le point de paramètre K.Le système
OE = E(K)
J = J(K) , K ∈ est la représentation paramétrique de la courbe (C) ou le système d'équations paramétrique de la courbe (C).quotesdbs_dbs26.pdfusesText_32[PDF] application dérivation 1s exercices
[PDF] les dangers de la radioactivité
[PDF] utilisation médicale du nucléaire avantages
[PDF] quelques applications de la radioactivité
[PDF] tomographie
[PDF] médecine nucléaire
[PDF] utilisation de la radioactivité en médecine
[PDF] generalite sur les ensembles et les applications
[PDF] ensemble application relation exercice
[PDF] formule trigonométrique 3eme
[PDF] problèmes conduisant ? une modélisation par des fonctions.
[PDF] application des suites numériques dans la vie
[PDF] application des mathématiques ? d autres disciplines capes
[PDF] oral capes maths
