 corrigé baccalauréat général - épreuve denseignement de spécialité
corrigé baccalauréat général - épreuve denseignement de spécialité
nombre de fois où elle s'est présentée à l'examen jusqu'à sa réussite. Ainsi Dérivation convexité
 Corrigé du baccalauréat ES/L Métropole 20 juin 2014
Corrigé du baccalauréat ES/L Métropole 20 juin 2014
20 juin 2014 Corrigé du baccalauréat ES/L Métropole 20 juin 2014. Exercice 1. 5 points. Commun à tous les candidats. 1. c. PA(B) = 1−PA(B) = 1−03 = 0
 Corrigé du baccalauréat Terminale ES/L Métropole - La Réunion
Corrigé du baccalauréat Terminale ES/L Métropole - La Réunion
13 sept. 2019 La convexité d'une fonction ... Le taux d'intérêt annuel moyen est d'environ 539%. Exercice 4. 5 points. Candidats de ES ayant suivi la ...
 Chapitre 3 : Exercices Continuité Convexité Terminale ES 2014
Chapitre 3 : Exercices Continuité Convexité Terminale ES 2014
Déterminer les intervalles sur lesquels f est convexe ou concave. c. La courbe représentative de la fonction f admet-elle un point d'inflexion ? Exercice 7. On
 Corrigé du baccalauréat Terminale ES/L Amérique du Nord 29 mai
Corrigé du baccalauréat Terminale ES/L Amérique du Nord 29 mai
29 mai 2018 On peut donc dire que parmi les rubans LED d'intérieur
 Correction du Baccalauréat ES/L Antilles-Guyane 18 juin 2019
Correction du Baccalauréat ES/L Antilles-Guyane 18 juin 2019
18 juin 2019 Exercice II. 5 points. Candidats de ES n'ayant pas suivi l ... f est convexe si f ′′ > 0. f ′′(x) est du signe de (02 + 0
 Corrigé du baccalauréat ES/L – Liban 29 mai 2018
Corrigé du baccalauréat ES/L – Liban 29 mai 2018
29 mai 2018 La fonction f est donc convexe sur l'intervalle [2; 5]. Réponse D ... Réponse B. Exercice 4. 5 points. Commun à tous les candidats. 1. Soit f ...
 CONTINUITÉ ET CONVEXITÉ : exercices
CONTINUITÉ ET CONVEXITÉ : exercices
CONTINUITÉ ET CONVEXITÉ : exercices. Exercice 1 - Fonction polynôme. Soit / la fonction Si oui donner les coordonnées du (ou des) point(s) d'inflexion de cf ...
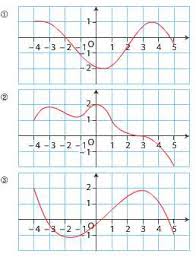 Exercices : convexité
Exercices : convexité
Terminale ES. Convexité. Exercices : convexité. Exercice 1 : Pour chaque courbe déterminer les intervalles sur lesquels la fonction f est convexe (
 Terminale ES
Terminale ES
Terminale ES. INTERROGATION ECRITE. Convexité. CORRIGÉ. Exercice 1 : QCM. /6. Pour chaque question cocher sur cette feuille la ou les bonnes réponses dans
 CONTINUITÉ ET CONVEXITÉ : exercices
CONTINUITÉ ET CONVEXITÉ : exercices
CONTINUITÉ ET CONVEXITÉ : exercices. Exercice 1 - Fonction polynôme. Soit / la fonction définie sur [-5 ; 5] par /(x)=2x3 + 3x2 - 12x + 1.
 Exercices : convexité
Exercices : convexité
Terminale ES. Convexité. Exercices : convexité. Exercice 1 : Pour chaque courbe déterminer les intervalles sur lesquels la fonction f est convexe (
 Continuité et convexité.
Continuité et convexité.
Sep 18 2017 DÉRIVATION
 Rappels sur la dérivabilité. Compléments et convexité - Lycée d
Rappels sur la dérivabilité. Compléments et convexité - Lycée d
EXERCICES. 11 juillet 2021 à 9:37. Rappels sur la dérivabilité. TERMINALE MATHS SPÉ ... Étudier la convexité de la fonction f sur R.
 DS n°3
DS n°3
Détermine graphiquement les intervalles sur lesquels cette fonction h est convexe ou concave. cf cg ' ch ''. Page 2. Exercice 2 :.
 bac-es-mathematiques-amerique-du-nord-2018-specialite-corrige
bac-es-mathematiques-amerique-du-nord-2018-specialite-corrige
May 29 2018 Sujet Mathématiques Bac 2018 • Corrigé ... EXERCICE n°4 (6 points) ... Étudier la convexité de la fonction ? sur l'intervalle 10; 50.
 Exercices sur la convexité
Exercices sur la convexité
Jan 30 2017 Terminale ES. Exercices sur la convexité. Exercice 1. Soit f la fonction définie sur R par f(x) = x5 ? 5x4. 1. Étudier la convexité de f.
 Corrigé du baccalauréat Terminale ES/L – Centres Étrangers juin
Corrigé du baccalauréat Terminale ES/L – Centres Étrangers juin
Jun 2 2019 Corrigé du baccalauréat Terminale ES/L – Centres Étrangers juin 2019. Exercice 1. 5 points ... Convexité de f convexe concave.
 Continuité et convexité – Exercices
Continuité et convexité – Exercices
Continuité et convexité – Exercices – Terminale ES/L – G. AURIOL Lycée Paul Sabatier. Continuité et convexité – Exercices. Variation de fonctions
 [PDF] CONTINUITÉ ET CONVEXITÉ : exercices - Maths91fr
[PDF] CONTINUITÉ ET CONVEXITÉ : exercices - Maths91fr
Exercice 2 - Étude d'une fonction à partir d'un tableau de variation Étudier enfin la convexité de la fonction / sur R N Peyrat Lycée Saint-Charles
 [PDF] IE910-Convexite-CORRIGEpdf
[PDF] IE910-Convexite-CORRIGEpdf
Terminale ES INTERROGATION ECRITE Convexité CORRIGÉ Exercice 1 : QCM /6 Pour chaque question cocher sur cette feuille la ou les bonnes réponses dans
 Dérivation continuité et convexité Maths Terminale ES exercices
Dérivation continuité et convexité Maths Terminale ES exercices
Dérivation continuité et convexité Maths Terminale ES exercices corrigés destinés aux élèves de Terminale ES Cours devoirs corrigés
 [PDF] Continuité et convexité – Exercices
[PDF] Continuité et convexité – Exercices
Continuité et convexité – Exercices – Terminale ES/L – G AURIOL Lycée Paul Sabatier Continuité et convexité – Exercices Variation de fonctions dérivées
 [PDF] Rappels sur la dérivabilité Compléments et convexité
[PDF] Rappels sur la dérivabilité Compléments et convexité
EXERCICES 24 novembre 2022 à 12:06 Rappels sur la dérivabilité TERMINALE MATHS SPÉ Si oui donner l'équation de cette ou ces tangente(s)
 [PDF] Exercices Continuité Convexité Terminale ES 2014 Lycée Lapérouse
[PDF] Exercices Continuité Convexité Terminale ES 2014 Lycée Lapérouse
Chapitre 3 : Exercices Continuité Convexité Terminale ES 2014 Lycée Lapérouse Exercice 1 Soit le tableau de variations de la fonction f définie sur [-5
 [PDF] Exercices : convexité
[PDF] Exercices : convexité
Terminale ES Convexité Exercices : convexité Exercice 1 : Pour chaque courbe déterminer les intervalles sur lesquels la fonction f est convexe (
 Terminale ES/Convexité - PDF Téléchargement Gratuit - DocPlayerfr
Terminale ES/Convexité - PDF Téléchargement Gratuit - DocPlayerfr
C - - O I C - C Convexité étude de fonctions Exercice 770 Parmi les Baccalauréat ES Antilles Guyane 12 septembre 2014 Corrigé EXERCICE 1 5 points Commun
 [PDF] Convexité fonctions exponentielles - C Lainé
[PDF] Convexité fonctions exponentielles - C Lainé
Terminale ES/L C Lainé CORRECTION DU DEVOIR SURVEILLÉ N° 5 Convexité et fonctions exponentielles Le 28 janvier 2020 Exercice 1
Lycée JANSON DE SAILLY18 septembre 2017
DÉRIVATION,CONTINUITÉ ET CONVEXITÉTleES
IDÉRIVÉES
1 TANGENTE À UNE COURBE
Soitfune fonction définie sur un intervalleI, dérivable enaoùaest un réel deI, etCfsa courbe représentative dans un repère du plan. La droite passant par le pointA(a;f(a))de la courbeCfet de coefficient directeurf?(a)est appelée la tangente à la courbeCfau point d"abscissea.0xy?i?
j af(a)ASoitfune fonction définie sur un intervalleI, dérivable enaoùaest un réel deI, etCfsa courbe
représentative dans un repère du plan. L"équation réduite de la tangente à la courbeCfau pointAd"abscisseaest : y=f?(a)×(x-a)+f(a)2 DÉRIVÉES DES FONCTIONS DE RÉFÉRENCE
fdéfinie sur ...f(x)f?(x)fdérivable sur ... Rk0RRax+baR
Rxnnxn-1Rpournentiern?2
R?1 x-1x2R? R?1 xn-nxn+1R?pournentiern?1 [0;+∞[⎷x12⎷x]0;+∞[
3 DÉRIVÉES ET OPÉRATIONS
uetvsont deux fonctions dérivables sur un intervalleI: •?u2??=2uu?•Sinest un entier non nul,(un)?=nun-1u? Si la fonctionvne s"annule pas sur l"intervalleI(siv(x)?=0 surI) •?1v? =-v?v2•?uv? ?=u?v-uv?v2A. YALLOUZ(MATH@ES)Page 1 sur18
Lycée JANSON DE SAILLY18 septembre 2017
DÉRIVATION,CONTINUITÉ ET CONVEXITÉTleES
4 DÉRIVÉE ET VARIATIONS D"UNE FONCTION
THÉORÈME1
Soitfune fonction dérivable et monotone sur un intervalleIdeR. Sifest constante surI, alors pour tout réelxappartenant àI,f?(x) =0. Sifest croissante surI, alors pour tout réelxappartenant àI,f?(x)?0. Sifest décroissante surI, alors pour tout réelxappartenant àI,f?(x)?0.Le théorème suivant, permet de déterminer les variations d"une fonction sur un intervalle suivant le signe de sa
dérivée.THÉORÈME2
Soitfune fonction dérivable sur un intervalleIdeRetf?la dérivée defsurI. Sif?est nulle surI, alorsfest constante surI. Sif?est strictement positive surI, sauf éventuellement en un nombre fini de points où elle s"annule,
alorsfest strictement croissante surI. Sif?est strictement négative surI, sauf éventuellement en un nombre fini de points où elle s"annule,
alorsfest strictement décroissante surI.THÉORÈME3
Soitfune fonction dérivable sur un intervalle ouvertIdeRetx0un réel appartenant àI.1. Sifadmet un extremum local enx0, alorsf?(x0) =0.
2. Si la dérivéef?s"annule enx0en changeant de signe, alorsfadmet un extremum local enx0.
x ax0b f ?(x)-|0|+ f(x) minimumx ax0b f ?(x)+|0|- f(x)maximumREMARQUES
1. Dans la proposition 2. du théorème 3 l"hypothèseen changeant de signeest importante.
Considérons la fonction cube définie surRparf(x) =x3qui a pour dérivée la fonction f ?définie surRparf?(x) =3x2. f ?(0) =0 et pour tout réelxnon nul,f?(x)>0. La fonction cube est strictement croissante surRet n"admet pas d"extremum en 0. 0xy2. Une fonction peut admettre un extremum local enx0sans être nécessairement dérivable.
Considérons la fonction valeur absoluefdéfinie surRparf(x) =|x|. fest définie surRpar :f(x) =?xsix?0 -xsix<0. fadmet un minimumf(0) =0 orfn"est pas dérivable en 0. 0xyA. YALLOUZ(MATH@ES)Page 2 sur18
Lycée JANSON DE SAILLY18 septembre 2017
DÉRIVATION,CONTINUITÉ ET CONVEXITÉTleES
EXEMPLE:ÉTUDE D"UNE FONCTION
Soitfla fonction définie surRparf(x) =1-4x-3
x2+1.1. Calculerf?(x).
SurRfest dérivable comme somme et quotient de deux fonctions dérivables. f=1-u vd"oùf?=-u?v-uv?v2. Avec pour tout réelx, u(x) =4x-3 d"oùu?(x) =4 v(x) =x2+1 d"oùv?(x) =2xSoit pour tout réelx,
f ?(x) =-4(x2+1)-2x(4x-3) (x2+1)2 =-4x2+4-8x2+6x (x2+1)24x2-6x-4
(x2+1)2 Ainsi,f?est la fonction définie surRparf?(x) =4x2-6x-4(x2+1)22. Étudier les variations de la fonctionf
Les variations de la fonctionfse déduisent du signe de sa dérivée.Étudions le signe def?(x) =4x2-6x-4
(x2+1)2:Pour tout réelx,(x2+1)2>0. Par conséquent,f?(x)est du même signe que le polynôme du second degré
4x2-6x-4 aveca=4,b=-6 etc=-4.
Le discriminant du trinôme estΔ=b2-4acSoit
Δ= (-6)2-4×4×(-4) =100
CommeΔ>0, le trinôme admet deux racines :
x1=-b-⎷
2aSoitx1=6-108=-12
etx2=-b+⎷2aSoitx2=6+108=2
Un polynôme du second degré est du signe deasauf pour les valeurs comprises entre les racines.Nous pouvons déduire le tableau du signe def?(x)suivant les valeurs du réelxainsi que les variations de la
fonctionf: x-∞-122+∞ f ?(x)+ 0-0+ f(x)5 0A. YALLOUZ(MATH@ES)Page 3 sur18
Lycée JANSON DE SAILLY18 septembre 2017
DÉRIVATION,CONTINUITÉ ET CONVEXITÉTleES
IICONTINUITÉ
1NOTION DE CONTINUITÉ
Soitfune fonction définie sur un intervalleIdeR.Intuitivement, dire quefest continue surIsignifie que sa courbe représentative peut être tracée en un seul
morceau (la courbe ne présente aucun saut, aucun trou).EXEMPLE ET CONTRE-EXEMPLE
Soitfune fonction définie sur un intervalleIetaun réel deI. On noteCfla courbe représentative de la fonctionfetAle point de la courbeCfd"abscissea. Pour tout réelxde l"intervalleI, on considère le pointMde la courbeCfd"abscissex O xy Cf aA f(a)xM f(x)Oxy C f aA f(a)xM f(x)La fonctionfest continue.
Pour tout réeladeI, on peut rendref(x)aussi proche que l"on veut def(a)pourvu quexsoit suffisamment proche dea.La fonctionfn"est pas continue ena. La courbeCfprésente un saut au point d"abscissea. Le pointMn"est pas proche du pointAquandxest proche dea.2PROPRIÉTÉS
THÉORÈME(admis)
Toute fonction dérivable sur un intervalleIest continue sur cet intervalle.REMARQUE
La réciproque du théorème est fausse :
Une fonction peut être continue en un réelasans être dérivable en ce réel. Par exemple la fonction valeur absoluefdéfinie surRparf(x) =|x|est contine en 0 mais n"est pas dérivable en 0. 0xyCONSÉQUENCES
On admettra les deux propriétés suivantes :
1. Les fonctions de référence (affines, carré, cube, inverse, racine carrée) sont continues sur tout intervalle où
elles sont définies.2. Toutefonction construite algébriquement (somme, produit, inverse, quotient ou composée) àpartir defonctions
de référence est continue sur tout intervalle où elle est définie.A. YALLOUZ(MATH@ES)Page 4 sur18
Lycée JANSON DE SAILLY18 septembre 2017
DÉRIVATION,CONTINUITÉ ET CONVEXITÉTleES
IIICONTINUITÉ ET ÉQUATION
1THÉORÈME DES VALEURS INTERMÉDIAIRES
THÉORÈME(admis)
Sifest une fonction définie sur un intervalleIet continue surIalors elle vérifie la propriété suivante :
quels que soient les réelsaetbde l"intervalleI, pour tout réelkcompris entref(a)etf(b), l"équation
f(x) =kadmet au moins une solutioncappartenant à[a;b].Ce théorème résulte du fait que l"image d"un intervalle deRpar une fonction continue est un intervalle deR.
fest continue surI fn"est pas continue surI 0 xy k a f(a)bf(b) 0xy k af(a) m f(b)m bL"image de l"intervalle[a;b]est un intervalle.
Tout réelkcompris entref(a)etf(b)est l"image
d"au moins un élément de[a;b].L"image de l"intervalle[a;b]n"est pas un intervalle. Il existe des réelskcompris entref(a)etf(b)pour lesquels l"équationf(x) =kn"a pas de solution.2THÉORÈME DE LA VALEUR INTERMÉDIAIRE
COROLLAIRE
Soitfune fonction définie sur un intervalleIdeReta,bdeux réels appartenant àI,a1. Existence
Par hypothèse,fest continue sur[a;b]alors d"après le théorème des valeurs intermédiaires, l"équation
f(x) =kadmet au moins une solutioncappartenant à[a;b].2. Unicité
Supposons que l"équationf(x) =kadmette deux solutions distinctesc1etc2appartenant à[a;b] Par hypothèse,fest strictement monotone sur[a;b]alorsc1?=c2?f(c1)?=f(c2) Ce qui aboutit à une contradiction puisquef(c1) =f(c2) =k Doncc1=c2, ce qui prouve que l"équationf(x) =kadmet une solution unique dans[a;b]REMARQUES
1. Sifest continue et strictement monotone sur[a;b]etf(a)×f(b)<0, alors l"équationf(x) =0 admet une
solution unique dans[a;b]A. YALLOUZ(MATH@ES)Page 5 sur18
Lycée JANSON DE SAILLY18 septembre 2017
DÉRIVATION,CONTINUITÉ ET CONVEXITÉTleES
2. Le théorème s"applique aussi lorsquefest continue et strictement monotone sur un intervalle de laforme
IVCONVEXITÉ
1FONCTION CONVEXE,FONCTION CONCAVE
DÉFINITIONS
Soitfune fonction dérivable sur un intervalleIetCfsa courbe représentative. Dire que la fonctionfest convexe surIsignifie que la courbeCfest située entièrement au-dessus de
chacune de ses tangentes. Dire que la fonctionfest concave surIsignifie que la courbeCfest située entièrement au-dessous de
chacune de ses tangentes.EXEMPLES
O xy Cf convexe Oxy Cf concaveconvexeLa fonction carréx?-→x2est convexe.La fonction inversex?-→1xest concave sur]-∞;0[et
convexe sur]0;+∞[REMARQUE
Intuitivement, quels que soient les pointsAetBde la courbeCf Si le segment[AB]est au-dessus de la courbe alorsfest convexe. Si le segment[AB]est au-dessous de la courbe alorsfest concave.Oxyaf(a)
bf(b)ABOxyaf(a)
bf(b) AB fest convexe.fest concaveA. YALLOUZ(MATH@ES)Page 6 sur18
Lycée JANSON DE SAILLY18 septembre 2017
DÉRIVATION,CONTINUITÉ ET CONVEXITÉTleES
THÉORÈME(admis)
Soitfune fonction définie et dérivable sur un intervalleI. fest convexe surIsi, et seulement si, sa fonction dérivéef?est croissante surI. fest concave surIsi, et seulement si, sa fonction dérivéef?est décroissante surI.CONSÉQUENCE
On notef??la dérivée seconde de la fonctionf, c"est à dire la dérivée de la dérivéef?.
Si la dérivée seconde est positive alors la fonctionfest convexe. Si la dérivée seconde est négative alors la fonctionfest concave.EXEMPLE
Soitfla fonction définie surRparf(x) =x5-5x4.
Sa dérivée est la fonctionf?définie surRparf?(x) =5x4-20x3. Sa dérivée seconde est la fonctionf??définie surRparf??(x) =20x3-60x2=20x2(x-3). Les variations def?se déduisent du signe de sa dérivéef??. Notons que 20x2?0 doncf??(x)est du même signe quex-3. D"où le tableau : x-∞3+∞ signe def??(x)- 0+ variations def? convexité defCONCAVECONVEXE fest concave sur]-∞;3]et convexe sur[3;+∞[.2POINT D"INFLEXION
DÉFINITION
Soitfune fonction définie et dérivable sur un intervalleIetCfsa courbe représentative.S"il existe un pointAde la courbeCftel que la courbe traverse sa tangente en ce point, alors on dit queA
est un point d"inflexion.EXEMPLE
La courbe représentative de la fonction cube définie surRparf(x) =x3admet comme point d"inflexion
l"origine O(0;0)du repère.quotesdbs_dbs35.pdfusesText_40[PDF] connexité exercices corrigés
[PDF] exercices convexité
[PDF] ensemble convexe exercices corrigés
[PDF] tp mps sciences et aliments
[PDF] mps sciences et art maths
[PDF] démontrer qu'une fonction est croissante sur un intervalle
[PDF] science et cosmétologie enseignement d exploration
[PDF] montrer qu'une fonction est croissante terminale s
[PDF] montrer qu'une fonction est croissante seconde
[PDF] démontrer qu'une fonction est croissante sur un intervalle donné
[PDF] tp mps svt
[PDF] site de recherche de personne gratuit
[PDF] fonction cube definition
[PDF] comment espionner quelqu un a distance
