 Fonction de Bessel dordre zéro
Fonction de Bessel dordre zéro
Exercice 2-4 : Fonction de Bessel d'ordre zéro a) Il est commode de considérer le logarithme de la valeur absolue du terme général : vk = log
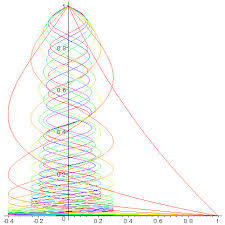 Les fonctions de Bessel
Les fonctions de Bessel
O n définit alors la fonction de Bessel Jν de première espèce d'ordre ν par le choix de 0. 1. 2 (1. ) a ν. = Γ +. ce qui perm et de donner une écriture com
 Lois de probabilités de Bessel
Lois de probabilités de Bessel
où : Ko (x) est la fonction de Bessel d'ordre 0 et de 2ème espèce (type K) définie comme suit : cf [3] p. 376 formule 9.6.22. On a ainsi la fonction de
 ( )0yn ( )0yn
( )0yn ( )0yn
Fonction de Bessel de 2ème espèce modifiée d'ordre n. (cf. Özisik pour la Comportement asymptotique des fonctions de Bessel d'ordre 0 et 1. Si u → 0 ...
 Equation de Bessel.pdf
Equation de Bessel.pdf
15 juil. 2015 une unique solution f0 DSE(0) vérifiant f0(0) = 1. Elle est définie ... Plus généralement on définit l'équation de Bessel d'ordre n par xy ...
 Fonctions de Bessel et combinatoire
Fonctions de Bessel et combinatoire
On démontre que leur série génératrice associée sont solutions d'équations différentielles d'ordre La fonction de Bessel modifiée de première espèce notée T
 Prépa. Agrég écrit dAnalyse avril 2003. Fonctions de Bessel
Prépa. Agrég écrit dAnalyse avril 2003. Fonctions de Bessel
particuli`ere donnée par la fonction de Bessel Jn qui est – `a un multiple pr`es – la solution de l'équation de Bessel d'ordre n qui reste bornée quand t → 0.
 CALCUL DINTEGRALES DE QUELQUES FONCTIONS DE
CALCUL DINTEGRALES DE QUELQUES FONCTIONS DE
Krn (x) = i
 Fonctions de Bessel
Fonctions de Bessel
ou Jn(m) est la fonction de Bessel de première espèce d'ordre n de la ≈0. ≈0. ≈0. ≈0. 0009. 0
 MEMOIRE THEME FONCTIONS DE BESSEL ET APPLICATIONS A
MEMOIRE THEME FONCTIONS DE BESSEL ET APPLICATIONS A
2 jan. 2020 que leurs relation avec les fonctions de Bessel d'ordre demi entier. ... 0 et y > 0. (1.1.5). Considérons la fonction f : t −→ tx-1(1 − t)y-1 ...
 Les fonctions de Bessel
Les fonctions de Bessel
fonction déterm inée la fonction de Bessel d'ordre 0
 Prépa. Agrég écrit dAnalyse avril 2004. Fonctions de Bessel Les
Prépa. Agrég écrit dAnalyse avril 2004. Fonctions de Bessel Les
deux entiers tels que 0 ? m < n les fonctions de Bessel Jm et Jn n'ont pas de ordre `a un syst`eme différentiel du premier ordre
 Fonctions de Bessel
Fonctions de Bessel
Les fonctions de Bessel sont des solutions des équations différentielles définies pour n ? R par. (En) x2y + xy + (x2 ? n2)y = 0. Pour n ? R la fonction
 ( )0yn ( )0yn
( )0yn ( )0yn
Fonction de Bessel de 1ère espèce non modifiée d'ordre n Comportement asymptotique des fonctions de Bessel d'ordre 0 et 1. Si u ? 0 : J0(u) ? 1.
 Fonction de Bessel dordre zéro
Fonction de Bessel dordre zéro
La formule de Stirling fournit l'approximation assez grossière log k! ? k log k ?k. Le terme le plus grand est déterminé par la condition dvk/dk = 0.
 01-Fonction-Gamma-et-fonctions-de-Bessel.pdf
01-Fonction-Gamma-et-fonctions-de-Bessel.pdf
et la fonction sous intégrale sera de l'ordre 1p x. ? pour. 0 x ? et ? ?. 1. 0. 1 a p dx x existera pour les mêmes valeurs de p pour.
 scipy : librairie pour la programmation scientifique
scipy : librairie pour la programmation scientifique
Fonctions spéciales (fonction de Bessel loi de distribution
 Lois de probabilités de Bessel
Lois de probabilités de Bessel
où : Ko (x) est la fonction de Bessel d'ordre 0 et de 2ème espèce (type K) définie comme suit : cf [3] p. 376 formule 9.6.22. On a ainsi la fonction de
 PartieI : Étude de la fonction J = J 0 de Bessel. Développement en
PartieI : Étude de la fonction J = J 0 de Bessel. Développement en
0. =13bis. ?. ?. ?. Fonction de Bessel. L'épreuve est constituée de trois parties et propose l'étude de quelques propriétés de Ca fonction J0 de.
 Etude de quelques fonctions spéciales
Etude de quelques fonctions spéciales
la fonction d'erreur la fonction Gamma et les fonctions de Bessel. Pour obtenir l'écriture intégrale de la fonction de Bessel d'ordre 0 on utilise ...
 [PDF] Exercice 2-4 : Fonction de Bessel dordre zéro
[PDF] Exercice 2-4 : Fonction de Bessel dordre zéro
Exercice 2-4 : Fonction de Bessel d'ordre zéro a) Il est commode de considérer le logarithme de la valeur absolue du terme général :
 [PDF] Les fonctions de Bessel - Promenades maths
[PDF] Les fonctions de Bessel - Promenades maths
fonction déterm inée la fonction de Bessel d'ordre 0 m ais plutôt que de faire ce travail dans le cas particulier du fil nous allons généraliser à
 [PDF] 01-Fonction-Gamma-et-fonctions-de-Besselpdf - Univ Bouira
[PDF] 01-Fonction-Gamma-et-fonctions-de-Besselpdf - Univ Bouira
Si on pose 0 2 x a = on aura: Fonction Gamma et fonctions de Bessel L'équation différentielle de Bessel est une équation linéaire d'ordre deux
 [PDF] Fonctions de Bessel et combinatoire - LACIM
[PDF] Fonctions de Bessel et combinatoire - LACIM
Les fonctions de Bessel apparaissent naturellement comme fonctions propres d'opérateurs différentiels liés à l'étude de certaines équations de la physique
 [PDF] Equations et fonctions de Bessel
[PDF] Equations et fonctions de Bessel
Fonction de Bessel de 1ère espèce non modifiée d'ordre n Comportement asymptotique des fonctions de Bessel d'ordre 0 et 1 Si u ? 0 : J0(u) ? 1
 [PDF] MEMOIRE THEME FONCTIONS DE BESSEL ET APPLICATIONS A
[PDF] MEMOIRE THEME FONCTIONS DE BESSEL ET APPLICATIONS A
2 jan 2020 · dont les solutions sont des fonctions de Bessel d'ordre ? où x est la variable y(x) la fonction inconnue et ? un paramètre réel Nous
 [PDF] Fonctions de Bessel - Fiche Pratique : http ://poujouly
[PDF] Fonctions de Bessel - Fiche Pratique : http ://poujouly
ou Jn(m) est la fonction de Bessel de première espèce d'ordre n de la variable m et dont les valeurs sont données sur le graphique et le tableau suivant
 [PDF] Analyse fonctionnelle
[PDF] Analyse fonctionnelle
La fonction Jn est appelée fonction de Bessel de première espèce d'ordre n Démonstration — La convergence de la série résulte de la convergence vers 0 du
 [PDF] Prépa Agrég écrit dAnalyse avril 2004 Fonctions de Bessel Les
[PDF] Prépa Agrég écrit dAnalyse avril 2004 Fonctions de Bessel Les
Les fonctions de Bessel peuvent servir `a illustrer un grand nombre des th`emes qui sont classiques `a l'oral de l'agrégation : fonctions définies par une
 [PDF] calcul dintegrales de quelques fonctions de bessel
[PDF] calcul dintegrales de quelques fonctions de bessel
L'intégrale I est une transformée de Bessel de la fonction u^ par la fonction KL o Elle est égale à : On peut la calculer par récurrence en partant de
UHA - ENSISA
ENSISA 1ere annee
Mathematiques: Outils pour le calcul scientique
Elisabeth REMM
Chapitre 2Etude de quelques fonctions specialesIntroduction: Le but de ce chapitre est d'etudier trois types de fonctions qui sont indispensables pour modeliser quelques phenomenes physiques comme les vibrations d'une membrane ou la diusion de la chaleur: la fonction d'erreur, la fonction Gamma et les fonctions de Bessel. Ces fonctions sont denies a partir d'integrales simples ou generalisees.1.La fonction d'erreur
1.1.Denition.
Denition 1.On appelle fonction d'erreur ou encore fonction d'erreur de Gauss, la fonction erf :R!R denie par erf(x) =2p Z x 0 et2dt Comme l'exponentielle est une fonction continue surRcette fonction est derivable et sa derivee est (erf)0(x) =2p
ex2>0: C'est donc une fonction croissante, paire. On demontre (voir chapitre 1) que l'integrale generalisee 2p Z +1 0 et2dt= 1 converge et la fonction erf a pour limite 1 en +1. Son graphe est le suivant1.2.Proprietes.La propriete suivante permet de faire du calcul numerique sur la fonction erf.
Proposition 1.La serie entiere
+1X n=0(1)n(2n+ 1)n!x2n+1 converge pour toutxreel (le rayon de convergence est inni). De plus on a erf(x) =2p +1X n=0(1)n(2n+ 1)n!x2n+1 Cette ecriture sous forme de somme de serie entiere permet de donner des valeurs approchees. 12 ENSISA Chapitre 2. Fonctions speciales
1.3.Applications de la fonction d'erreur.La fonction erreur erf permet d'exprimer la marge
d'erreur des evaluations statistiques Son complement erfc (deni par erfc(x) = 1erf(x)) intervient dans des problemes de diusion: - diusion de la chaleur dans un milieux semi-inni a temperature de surface constante - diusion des especes chimiques dans des milieux quasi-inni a concentration supercielle con- stante.Voici deux exemples classiques d'applications.
(1) La loi normale centree reduite en probabilite. SoitXune variable aleatoire sur un espace probabilise ( ;;P). Rappelons que est la tribu des evenements etPest la probabilite denie sur . La loi de probabilite deX est la probabilite: PX(]a;b]) =P(f!2
;a < !bg) La fonction de repartition deXest la fonction d'une variable reelle:F(x) =P(fXxg)
La fonction de densitefest une fonction d'une variable reelle positive telle queF(x) =Z
x 1 f(t)dt;Z +1 1 f(t)dt= 1: Denition 2.On appelle loi normale centree la loi de densite g0;(x) =1
ex222 Cette loi permet en particulier de trouver des approximations de la loi de Bernoulli ou de la loi binomiale. Rappelons qu'une variable aleatoire suit la loi de Bernoulli si elle ne prend que deux valeurs 1 avec la probabilite p et 0 avec la probabiliteq= 1p. Par exemple on lance une piece donc il n'y a que deux issues pile ou face. Autre exemple on teste un individu au coronavirus: il n'y a que deux issues positif ou negatif. lci a loi de probabilite deXest PX(f1g) =p; PX(f0g) = 1p:
La loi binomiale correspond a la somme dentirages independants suivant chacun la loi de Bernoulli. (par exemple on lancenfois la pieces ou on testenindividus) La loi de probabilite correspond a la probabilite d'avoirksucces lorsqu'on faitnexperiences. Elle est donnee par PX(fkg) =k
n p k(1p)nk: Lorsquenetksont grands, ce coecient binomial est dicile a calculer. On utilise alors une approximation avec la loi normale plus precisemment sinpqest grand par rapport a 1 alors PX(fkg) =k
n p k(1p)nk'1pnpq g0;1(knppnpqElisabeth Remm 3
Par exemple on teste 10000 individus et la probabilite pour que 500 soient positifs est egale a PX(f500g) =500
100000;5500(0;5)9500:
en supposant que la probabilite d'^etre positif est 0;5. Ce resultat est pratiquement impos- sible a calculer donc on l'approxime par la loi normale. (2) Solutions de l'equation de la chaleur On s'interesse ici a un probleme de diusion de la chaleur dans le cas unidimensionnel (par exemple sur un l mais pas sur une surface). Le probleme consiste a trouver la fonction temperatureT(x;t) ouxest l'abscisse du point suite a un parametrage de l'espace unidimensionel ettle temps. Cette fonction temperature est solution de l'equation@@t @2@x 2T(x;t) =(x;t)
ouest une fonction donnee correspondant a une source de chaleur etun coecient de diusion thermique. On s'interessera plus tard a la resolution de cette equation apres avoir introduit la notion de transformation de Fourier. Par exemple, si l'espace unidimensionel est modelise parR+c'est a dire une demi-regle innie, et si en l'instant initialtla temperature est uniforme et egale aT1, en supposant que l'originex0soit portee et maintenue a la temperatureT2, alorsT(x;t) =T2(T2T1)erf(x2
pt On remarque que cette solution correspond a une vitesse de propagation de la chaleur innie. Cette solution est a manipuler avec precaution mais elle est satisfaisante dans la plupart des phenomenes thermiques.2.La fonction Gamma d'Euler
2.1.Denition.
Denition 3.La fonctionest denie pour toutx >0par l'integrale generalisee a parametre (x) =Z +1 0 ettx1dt: Regardons quelles sont les valeurs dextelles que (x) existe. Soit la fonction f:R]0;+1[!R (x;t)7!ettx1 (elle est bien denie surR]0;+1[ puisquetx1=e(x1)lntdonc pourtdans ]0;+1[ ) et pour toutx2Rla fonction f x: ]0;+1[!R t7!ettx1 est continue sur ]0;+1[ donc elle est localement integrable cad Z b a f x(t)dt=Z b a f(x;t)dt4 ENSISA Chapitre 2. Fonctions speciales
existe pour tout [a;b]2]0;+1[. Probleme on a Z +1 0 ettx1dt: donc on a +1donc une integrale generalisee en +1, et en 0fxn'est pas denie en 0 (cad quand t= 0) puisquetx1=e(x1)lntetlnn'est pas deni en 0 donc l'integrale est aussi generalisee en 0Pour montrer queR+1
0ettx1dtconverge il sut pour una >0 de montrer queRa
0ettx1dt
converge etR+1 aettx1dtconverge. La fonctionfxest positive sur ]0;+1[. On peut donc utiliser les criteres d'equivalence, de comparaison, etc... La limite en 0 deetest 1, donc quandtest proche de 0, on a e ttx10tx1=1t 1x et l'integrale Z1 01t 1xdt converge (integrale de Riemann convergente en 0) si 1x <1 doncx >0, et par equivalence l'integrale Z 1 0 ettx1dt converge pourx >0. La convergence de la deuxieme integrale peut se montrer en utilisant la propriete suivante: Pourxxe on a lim t+1t2ettx1= 0 donc pourtassez grand t2ettx1<1
soit e ttx1<1t 2 etZ+1 11t 2dt converge (integrale de Riemann convergente en +1) donc par comparaisonR+11ettx1dtcon-
verge.En conclusion pourx >0 l'integraleR+1
0ettx1dtconverge donc est denie surx >0.
2.2.Derivabilite de la fonction.
Theoreme 1.La fonctionest derivable sur]0;+1[et sa derivee est donnee par0(x) =Z
+1 0 et(lnt)tx1dt:Elisabeth Remm 5
C'est une consequence directe du theoreme de derivation. En eet, si f(x;t) =ettx1 alors @f(x;t)@x =et(lnt)tx1: Rappelons en eet quetx1=e(x1)ln(t)et donc la derivee par rapport axest ln(t)e(x1)ln(t). Pour tout intervalle ferme [a;b]]0;+1[, on peut majorer cette derivee partielle par une fonction integrableet(lnt)max(ta1;tb1) et donc le theoreme de derivation s'applique. Theoreme 2.La fonctionGammaverie l'equation fonctionnelle (x+ 1) =x(x); de plus (1) = 1 Demonstration.Une integration par partie nous donne, pour toutx >0:Z +1 0 ettx1dt= e ttxx +1 0 +Z +1 0t xx etdt=1x Z +1 0 txetdt car limt!0txet= 0 et limt!+1txet= 0quotesdbs_dbs35.pdfusesText_40[PDF] multiple de 13 entre 1 et 1000
[PDF] multiple de 12
[PDF] multiple de 19
[PDF] fonction de bessel j0
[PDF] table de 13
[PDF] fonction de bessel pdf
[PDF] fonction de bessel modifiée
[PDF] introduction ? la microéconomie varian pdf
[PDF] cours microeconomie 1 pdf
[PDF] cours de microéconomie licence 1 pdf
[PDF] corrélation multiple
[PDF] correlation multiple r
[PDF] exercice fonction cout de production
[PDF] corrélation multiple définition
