 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. I. Limites en l'infini. 1) Limite infinie à l'infini. Définition 1 : Soit f une fonction définie au moins sur un intervalle du type [a;+
 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. I. Limites en l'infini. 1) Limite infinie à l'infini. Définition 1 : Soit f une fonction définie au moins sur un intervalle du type [α
 Chapitre 4 - Limites et Asymptotes
Chapitre 4 - Limites et Asymptotes
Exercice 2.1 Vérifier si la fonction de l'Exercice 1.3 poss`ede une asymptote horizontale. On calcule la limite lim x→∞. 4 - x2 x2 + 3x + 2.
 LIMITES DES FONCTIONS
LIMITES DES FONCTIONS
( ) = la droite d'équation = est appelée asymptote horizontale à la courbe de la fonction en +∞. Page 3. Yvan Monka – Académie de Strasbourg –
 LIMITES & ASYMPTOTES ( )
LIMITES & ASYMPTOTES ( )
LIMITES & ASYMPTOTES. I) Limtites en + õ et en – õ. 1) Limites intuitives (A Savoir !) Théorèmes (admis): et. 2) Limite des fonctions polynômes. Théorème : ...
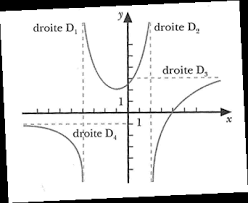 Chapitre 9: Identifier la position des asymptotes dune fonction grâce
Chapitre 9: Identifier la position des asymptotes dune fonction grâce
Identifier les asymptotes verticales. Exercice 9.2. Évaluer la limite suivante afin de reconnaître l'existence ou non d'une asymptote verticale.
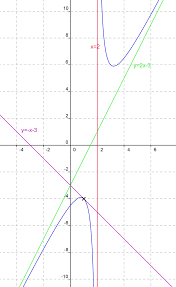 Limites de fonctions et asymptotes - Exercices Fiche 2
Limites de fonctions et asymptotes - Exercices Fiche 2
Déterminer la limite de f en + et en - . 4. Montrer que la courbe C f représentative de la fonction f admet une asymptote en + et en - .
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
limite ou asymptote verticale) de son domaine de définition. Mais la notion de limite s'utilise également pour appréhender le comportement de la courbe.
 1 Limites et comportement asymptotique Exercices corrigés
1 Limites et comportement asymptotique Exercices corrigés
• Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe. (asymptote verticale et asymptote horizontale). • Exercice 2
 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. I. Limites en l'infini. 1) Limite infinie à l'infini. Définition 1 : Soit f une fonction définie au moins sur un intervalle du type
 Compléments sur les limites asymptotes et continuité - Lycée d
Compléments sur les limites asymptotes et continuité - Lycée d
27 févr. 2017 2.2 Limite en l'infini d'une fonction rationnelle . . . . . . . . . . . . . . 6. 3 Asymptote oblique. 7. 4 Limites indéterminées avec des ...
 Chapitre 4 - Limites et Asymptotes
Chapitre 4 - Limites et Asymptotes
Exercice 2.1 Vérifier si la fonction de l'Exercice 1.3 poss`ede une asymptote horizontale. On calcule la limite lim x??. 4 - x2 x2 + 3x + 2.
 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. A Limites et infini. Soit f une fonction. 1- Limite infinie en l'infini. Lorsque f (x) peut être rendu supérieur à tout réel positif
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
La notion de limite est particulièrement utile pour étudier le comportement d'une fonction au voisinage d'un trou ou d'un bord (point limite ou asymptote
 LIMITES DES FONCTIONS
LIMITES DES FONCTIONS
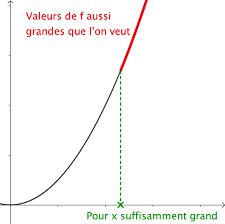
Lorsque x tend vers +? la courbe de la fonction "se rapproche" de son asymptote. 2) Limite infinie à l'infini. Intuitivement :.
 Limites asymptotes EXOS CORRIGES
Limites asymptotes EXOS CORRIGES
1 (cf exercice précédent) étudiez les limites en 0 des fonctions : 2) Etudier le comportement de f en + ? (limite
 Limites et asymptotes
Limites et asymptotes
Théorème : la limite en +o (ou en .o) d'une fonction rationnelle est donnée par la limite du quotient de ses termes de plus haut degré. b) Asymptote horizontale
 Limites de fonctions
Limites de fonctions
Asymptote verticale : la droite d ? x = a ( a ? R ) est une asymptote verticale au graphique de la fonction f si et seulement si la limite à gauche ou la
 I Exercices
I Exercices
Chapitre 2 : Limites et asymptotes. I Exercices. 1 Limites sans indétermination de f (notée (Cf )) admet une asymptote horizontale ou verticale.
Compléments sur les limites,
asymptotes et continuitéTable des matières
1 Limites finies ou infinies en l"infini2
1.1 Limites finies à l"infini. . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Limites infinies en l"infini. . . . . . . . . . . . . . . . . . . . . . . . 3
1.3 Limites infinies en un point. . . . . . . . . . . . . . . . . . . . . . . 4
1.4 Limite finie en un point. . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.5 Limites à droite, à gauche. . . . . . . . . . . . . . . . . . . . . . . . 5
2 Limite en l"infini des polynômes et fonctions rationnelles6
2.1 Limite en l"infini d"un polynôme. . . . . . . . . . . . . . . . . . . . 6
2.2 Limite en l"infini d"une fonction rationnelle. . . . . . . . . . . . . . 6
3 Asymptote oblique7
4 Limites indéterminées avec des radicaux9
4.1 Une simple indétermination. . . . . . . . . . . . . . . . . . . . . . . 9
4.2 Une double indétermination. . . . . . . . . . . . . . . . . . . . . . . 11
5 Continuité12
5.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
5.2 Règles opératoires. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
5.3 Conséquences. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
PAUL MILAN1VERS LE SUPÉRIEUR
1. LIMITES FINIES OU INFINIES EN L"INFINI
1 Limites finies ou infinies en l"infini
1.1 Limites finies à l"infini
Dire qu"une fonctionfa pour limite
?en+∞, signifie que tout intervalle ouvert centré en?, contient toutes les valeurs def(x)pourxassez grand - c"est à dire pour lesxd"un intervalle ]A;+∞[.Aétant à déterminer.On obtient une définition plus rigou-
reuse avec des quantificateurs : A xOC fΔ Définition 1 :Soit une fonctionfdéfinie surD=]a;+∞[.On écrira lim
x→+∞f(x)=?ou lim+∞f=?si, et seulement si, ??>0,?A>0,?x?D,x>A? |f(x)-?|Exemple :Montrons que limx→+∞2x-1x+1=2. ?2x-1 x+1-2???? =????2x-1-2x-2x+1???? =????-3x+1???? ?3xet3x3?. d"où ??>0,?A=3 ?,?x?]0 ;+∞[,x>A?????2x-1x+1-2???? Définition 2 :Soit une fonctionfdéfinie surD=]-∞;b[.On écrira lim
x→-∞f(x)=?ou lim-∞f=?si, et seulement si, ??>0,?B<0,?x?D,x1. LIMITES FINIES OU INFINIES EN L"INFINI
1.2 Limites infinies en l"infini
Dire qu"une fonctionfa pour limite
+∞en+∞, signifie que tout intervalle ]M;+∞|contient toutes les valeurs de f(x)pourxassez grand - c"est à dire pourx?]A;+∞[,Aétant à déterminer.On obtient une définition plus rigou-
reuse avec des quantificateurs : A]M Cf O Définition 3 :Soit une fonctionfdéfinie surD=]a;+∞[.On écrira lim
x→+∞f(x)=+∞ou lim+∞f=+∞si, et seulement si, ?M>0,?A>0,?x?D,x>A?f(x)>M "Pour tout réel positif M (aussi grand soit-il), on peut trouver un réel positif A tel que pour tout x de D supérieur à A alors f(x)est supérieur à M ». Exemple :Montrons que limx→+∞lnx= +∞ La fonction ln est définie sur]0 ;+∞[. SoitM>0. lnx>M?x>eM, on a donc ?M>0,?A=eM,?x?]0 ;+∞[,x>A?lnx>M Définition 4 :On définit de façon analogue : Soit une fonctionfdéfinie surD=]a;+∞[.On écrira lim
x→+∞f(x)=-∞ou lim+∞f=-∞si, et seulement si, ?m<0,?A>0,?x?D,x>A?f(x)On écrira lim
x→-∞f(x)=-∞ou lim-∞f=-∞si, et seulement si, ?m<0,?B<0,?x?D,x1. LIMITES FINIES OU INFINIES EN L"INFINI
1.3 Limites infinies en un point
Dire qu"une fonctionfa pour limite
+∞ena, signifie que tout intervalle ]M;+∞|contient toutes les valeurs de f(x)pourxassez proche dea- c"est à dire pour lesxd"un intervalle ouvert de rayonηcontenanta. Le rayonηétant à déterminerOn obtient une définition plus rigou-
reuse avec des quantificateurs a[]C fM O Définition 5 :Soit une fonctionfdéfinie surD=]b;a[?]a;c[.On écrira lim
x→af(x)= +∞ou limaf= +∞si, et seulement si, ?M>0,?η>0,?x?D,|x-a|<η?f(x)>M "Pour tout réel positif M (aussi grand soit-il), on peut trouver un réel positifηtel que pour tout x de D dans]a-η;a+η[alors f(x)est supérieur à M ». La droiteΔd"équationx=aest diteasymptote verticaleàCfau pointa. Remarque :L"intervalleD=]b;a[?]a;c[est appelévoisinagedea. La fonction fdoit être définie dans un voisinage deatout en étant non définie ena.Exemple :Montrer que limx→12x+1
(x-1)2= +∞Pourx>0 etx?=1, on a2x+1
(x-1)2?1(x-1)2et 1 (x-1)2>M?(x-1)2<1M? |x-1|<1⎷M, on a donc : ?M>0,?η=1 ⎷M,?x?D,|x-1|<η?f(x)>M Définition 6 :Soit une fonctionfdéfinie surD=]b;a[?]a;c[.On écrira lim
x→af(x)=-∞ou limaf=-∞si, et seulement si, ?m<0,?η>0,?x?D,|x-a|<η?f(x)PAUL MILAN4VERS LE SUPÉRIEUR
1. LIMITES FINIES OU INFINIES EN L"INFINI
1.4 Limite finie en un point
Dire qu"une fonctionfa pour limite?
ena, signifie que tout intervalle ouvert centré en?contient toutes les valeurs def(x)pourxassez proche dea- c"està dire pour lesxd"un intervalle ouvert
à déterminer.
On obtient une définition plus rigou-
reuse avec des quantificateurs a? O Définition 7 :Soit une fonctionfdéfinie surD=]b;a[?]a;c[.On écrira lim
x→af(x)=?ou limaf=?si, et seulement si, ??>0,?η>0,?x?D,|x-a|<η? |f(x)-?|1.5 Limites à droite, à gauche Définition 8 :Soitfune fonction définie sur un voisinageDdea. On dit que fadmet une limite : A droite dea, notée limx→ax>af(x)ou limx→a+f(x)ou lima+f, si et seulement si : limite finie?:??>0,?η>0,?x?D,aM,?x?D, 1M
PAUL MILAN5VERS LE SUPÉRIEUR
2. LIMITE EN L"INFINI DES POLYNÔMES ET FONCTIONS RATIONNELLES
Pourx<1 etm<0,3x-13m?x>1+3m, d"où :
?m<0,?η=-3 m,?x?D, 1-η2.1 Limite en l"infini d"un polynôme
Théorème 1 :Un polynôme a même limite en+∞et en-∞que son monôme du plus haut degré.SiP(x) =n∑
i=0a ixi=anxn+an-1xn-1+···+a0alors lim x→+∞P(x) =limx→+∞anxnet limx→-∞P(x) =limx→-∞anxn Démonstration :On met en facteur le monôme du plus haut degré,an?=0 :P(x) =n∑
i=0a ixi=anxn?1+n-1∑
i=0a i an×1xn-i? or?i??0 ;n-1?, limx→+∞1 xn-i=limx→-∞1xn-i=0, d"où par somme et produit : lim x→+∞P(x) =limx→+∞anxnet limx→-∞P(x) =limx→-∞anxn Exemple :Limites en+∞et-∞du polynômePtel que :P(x) =4x3+2x2+4On a : lim
x→+∞P(x) =limx→+∞4x3= +∞et limx→-∞P(x) =limx→-∞4x3=-∞
2.2 Limite en l"infini d"une fonction rationnelle
Théorème 2 :Une fonction rationnelle a même limite en+∞et-∞que son monôme du plus degré de son numérateur sur celui de son dénominateur.Sif(x) =n∑
i=0a ixi m∑ j=0b lim x→+∞f(x) =limx→+∞a nxn bmxmet limx→-∞f(x) =limx→-∞a nxnbmxmPAUL MILAN6VERS LE SUPÉRIEUR
3. ASYMPTOTE OBLIQUE
Démonstration :On met en facteur les monômes du plus haut degré du nu- mérateur et du dénominateur,an?=0,bm?=0 f(x) =n∑ i=0a ixi m∑ j=0b jxj=a nxn?1+n-1∑
i=0a i an×1xn-i? bmxm?1+m-1∑
j=0b jbm×1xm-j? ?i??0 ;n-1?, limx→+∞1xn-i=limx→-∞1xn-i=0, ?j??0 ;m-1?, limx→+∞1xm-j=limx→-∞1xm-j=0, parsomme,produit,quotient: lim x→+∞f(x) =limx→+∞a nxn bmxmet limx→-∞f(x) =limx→-∞a nxnbmxmExemple :
Déterminer la limite en+∞de la fonctionfdéfinie par :f(x) =2x2-3x+6x-1. lim x→+∞f(x) =limx→+∞2x2 x=limx→+∞2x= +∞ Déterminer la limite en-∞de la fonctiongdéfinie par :g(x) =4x2+3x-53x2-1 lim x→-∞g(x) =limx→-∞4x23x2=limx→-∞43=43
3 Asymptote oblique
Définition 9 :Une courbeCfreprésentant une fonctionfadmet uneasymp- tote obliqued"équationy=ax+ben+∞ou en-∞si et seulement si : lim x→+∞[f(x)-(ax+b)]=0 ou limx→-∞[f(x)-(ax+b)]=0 Remarque :La courbe se rapproche de plus en plus de la droite asymptote lorsquexdevient de plus en plus grand soit en valeur positive soit en valeur négative. Exemple :On obtient la courbeCfet son asymptotedsuivantes : O Cf dPAUL MILAN7VERS LE SUPÉRIEUR
3. ASYMPTOTE OBLIQUE
Théorème 3 :Dans une fonction rationnellef, lorsque le degré du polynôme du numérateurnet celui de son dénominateurmsont tels quen=m+1, alors la courbe représentativeCfadmet une asymptote obliqueden+∞et-∞.Soitf(x) =P(x)
Q(x)etd◦P=d◦Q+1
Soit la droite d d"équationy=ax+balors limx→∞[f(x)-(ax+b)] =0 Exemple :Soit la fonction définie surR-{-1}par :f(x) =2x2-3x+1x+1 Déterminer l"asymptote oblique deCfen+∞et-∞. On précisera de plus la position de la courbe par rapport à l"asymptote. Le numérateur de la fonctionfest de degré 2 et celui de son dénominateur est de degré 1, donc la courbeCfadmet une asymptote en+∞et en-∞. Pour déterminer cette asymptote, il faut décomposerfen éléments simples. Dé- terminons les coefficienta,betctel que :f(x) =ax+b+c x+1. Il y a deux méthode pour déterminer ces coefficients.1reméthode : par identification
On réduit la deuxième forme au même dénominateur puis on identifie à la première forme. f(x) =(ax+b)(x+1) +c x+1=ax2+ax+bx+b+cx+1=ax2+ (a+b)x+b+cx+1 Par identification, on obtient le système suivant : ?a=2 a+b=-3 b+c=1??????a=2 b=-5 c=6soitf(x) =2x-5+6 x+12eméthode : par division euclidienne
On effectue une division en basex. On a alors :
2x2-3x+1
x+1 -2x2-2x0x2-5x+1
+5x+5 0x+62x-5On a alors :f(x) =2x-5+6x+1
Montrons maintenant que la droite d"équationy=2x-5 est asymptote à la courbe defen+∞et-∞. On calcule :f(x)-(2x-5) =6 x+1.PAUL MILAN8VERS LE SUPÉRIEUR
4. LIMITES INDÉTERMINÉES AVEC DES RADICAUX
limx→+∞x+1= +∞donc par quotient limx→+∞6x+1=0 lim x→-∞x+1=-∞donc par quotient limx→-∞6 x+1=0, d"où lim x→+∞[f(x)-(2x-5)] =0 et limx→-∞[f(x)-(2x-5)] =0 La droite d"équationy=2x-5 est asymptote à la courbe defen+∞et-∞.Déterminons le signe def(x)-(2x-5) =6
x+1pour connaître la position de l"asymptote par rapport à la courbe. Le signe de 6 x+1est du signe dex+1 x f(x)-(2x-5) -∞-1+∞ 0+ La courbe est au dessus de l"asymptote en+∞et en dessous en-∞.On obtient la courbe suivante :
51015-5 -10 -15 -201 2 3 4 5 6-1-2-3-4-5-6-7y=2x-5 Cf O
4 Limites indéterminées avec des radicaux
4.1 Une simple indétermination
Soit la fonctionfdéfinie surRpar :f(x) =⎷
x2+1+x1) Déterminer la limite de la fonctionfen-∞.
2) a) Tracer la courbeCfpuis conjecturer une asymptote obliqueΔen+∞.
b) Démontrer cette conjecture.PAUL MILAN9VERS LE SUPÉRIEUR
4. LIMITES INDÉTERMINÉES AVEC DES RADICAUX
1) Le premier terme⎷x2+1 tend vers+∞tandis que le deuxièmextend vers
-∞lorsquextend vers-∞(+∞-∞) Pour lever l"indétermination, on multiplie par la quantité conjuguée : f(x) =(⎷ Il suffit alors de déterminer la limite de ce dénominateur pour trouverla limite de la fonctionfen-∞ lim x→-∞x2+1= +∞ lim x→+∞⎷ x= +∞???Par composition
lim x→-∞?x2+1= +∞Comme lim
x→-∞-x= +∞par somme limx→-∞⎷ x2+1-x= +∞Par quotient, on a alors : lim
x→-∞f(x) =0 Remarque :La courbeCfadmet l"axe des abscisses comme asymptote hori- zontale en-∞.2) a) À l"aide d"une calculette on peut visualiser la courbeCf. D"après l"allure de
la courbe, on peut conjecturer que la courbe admet la droiteΔd"équation y=2xcomme asymptote oblique comme le montre la graphique suivant : 123451 2 3-1-2-3-4-5-6-7
Cf O b) La fonctionftend manifestement vers+∞en+∞car somme de deux est asymptote à la courbe en+∞, étudions la limite en+∞de la quantité f(x)-2x.PAUL MILAN10VERS LE SUPÉRIEUR
4. LIMITES INDÉTERMINÉES AVEC DES RADICAUX
?x>0,f(x)-2x=?x2+1+x-2x=|x|?1+1x2-x=x? ?1+1x2-1? x?1+1x2-1??
?1+1x2+1??1+1x2+1=x?
1+1 x2-1??1+1x2+1
1 x? ?1+1x2+1? >0quotesdbs_dbs47.pdfusesText_47[PDF] limite et continuité exercices
[PDF] limite et continuité exercices corrigés bac science
[PDF] limite et continuité pdf
[PDF] limite et continuité terminale s
[PDF] Limite et Factoriel
[PDF] Limite et image de fonction
[PDF] Limite et suite
[PDF] limite exponentielle en 0
[PDF] limite exponentielle et logarithme
[PDF] Limite finie de suite
[PDF] limite fonction
[PDF] limite fonction racine nième
[PDF] limite fonction rationnelle en 0
[PDF] limite fonction trigonométrique exercice corrigé
