 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. I. Limites en l'infini. 1) Limite infinie à l'infini. Définition 1 : Soit f une fonction définie au moins sur un intervalle du type [a;+
 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. I. Limites en l'infini. 1) Limite infinie à l'infini. Définition 1 : Soit f une fonction définie au moins sur un intervalle du type [α
 Chapitre 4 - Limites et Asymptotes
Chapitre 4 - Limites et Asymptotes
Exercice 2.1 Vérifier si la fonction de l'Exercice 1.3 poss`ede une asymptote horizontale. On calcule la limite lim x→∞. 4 - x2 x2 + 3x + 2.
 LIMITES DES FONCTIONS
LIMITES DES FONCTIONS
( ) = la droite d'équation = est appelée asymptote horizontale à la courbe de la fonction en +∞. Page 3. Yvan Monka – Académie de Strasbourg –
 LIMITES & ASYMPTOTES ( )
LIMITES & ASYMPTOTES ( )
LIMITES & ASYMPTOTES. I) Limtites en + õ et en – õ. 1) Limites intuitives (A Savoir !) Théorèmes (admis): et. 2) Limite des fonctions polynômes. Théorème : ...
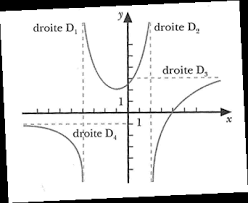 Chapitre 9: Identifier la position des asymptotes dune fonction grâce
Chapitre 9: Identifier la position des asymptotes dune fonction grâce
Identifier les asymptotes verticales. Exercice 9.2. Évaluer la limite suivante afin de reconnaître l'existence ou non d'une asymptote verticale.
 Compléments sur les limites asymptotes et continuité - Lycée d
Compléments sur les limites asymptotes et continuité - Lycée d
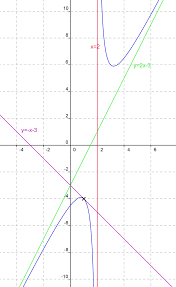
27 févr. 2017 1) Déterminer la limite de la fonction f en −∞. 2) a) Tracer la courbe Cf puis conjecturer une asymptote oblique ∆ en +∞. b) Démontrer cette ...
 Limites de fonctions et asymptotes - Exercices Fiche 2
Limites de fonctions et asymptotes - Exercices Fiche 2
Déterminer la limite de f en + et en - . 4. Montrer que la courbe C f représentative de la fonction f admet une asymptote en + et en - .
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
limite ou asymptote verticale) de son domaine de définition. Mais la notion de limite s'utilise également pour appréhender le comportement de la courbe.
 1 Limites et comportement asymptotique Exercices corrigés
1 Limites et comportement asymptotique Exercices corrigés
• Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe. (asymptote verticale et asymptote horizontale). • Exercice 2
 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. I. Limites en l'infini. 1) Limite infinie à l'infini. Définition 1 : Soit f une fonction définie au moins sur un intervalle du type
 Compléments sur les limites asymptotes et continuité - Lycée d
Compléments sur les limites asymptotes et continuité - Lycée d
27 févr. 2017 2.2 Limite en l'infini d'une fonction rationnelle . . . . . . . . . . . . . . 6. 3 Asymptote oblique. 7. 4 Limites indéterminées avec des ...
 Chapitre 4 - Limites et Asymptotes
Chapitre 4 - Limites et Asymptotes
Exercice 2.1 Vérifier si la fonction de l'Exercice 1.3 poss`ede une asymptote horizontale. On calcule la limite lim x??. 4 - x2 x2 + 3x + 2.
 Limites et asymptotes
Limites et asymptotes
Limites et asymptotes. A Limites et infini. Soit f une fonction. 1- Limite infinie en l'infini. Lorsque f (x) peut être rendu supérieur à tout réel positif
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
La notion de limite est particulièrement utile pour étudier le comportement d'une fonction au voisinage d'un trou ou d'un bord (point limite ou asymptote
 LIMITES DES FONCTIONS
LIMITES DES FONCTIONS
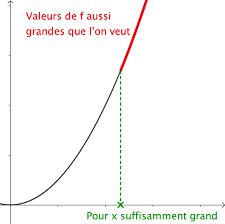
Lorsque x tend vers +? la courbe de la fonction "se rapproche" de son asymptote. 2) Limite infinie à l'infini. Intuitivement :.
 Limites asymptotes EXOS CORRIGES
Limites asymptotes EXOS CORRIGES
1 (cf exercice précédent) étudiez les limites en 0 des fonctions : 2) Etudier le comportement de f en + ? (limite
 Limites et asymptotes
Limites et asymptotes
Théorème : la limite en +o (ou en .o) d'une fonction rationnelle est donnée par la limite du quotient de ses termes de plus haut degré. b) Asymptote horizontale
 Limites de fonctions
Limites de fonctions
Asymptote verticale : la droite d ? x = a ( a ? R ) est une asymptote verticale au graphique de la fonction f si et seulement si la limite à gauche ou la
 I Exercices
I Exercices
Chapitre 2 : Limites et asymptotes. I Exercices. 1 Limites sans indétermination de f (notée (Cf )) admet une asymptote horizontale ou verticale.
Limites et asymptotes 1/3 LIMITES ET ASYMPTOTES
I) Limites des fonctions de référence
A l'infini
· Pour tout entier n > 0 : limn
xx®+¥=+¥ ; 1lim0n xx®+¥= ;· si n est pair : limn
xx®-¥=+¥ ; 1lim0n xx+· si n est impair : limn
xx®-¥=-¥ ; 1lim0n xx-· lim
xx®+¥=+¥ ; 1lim0x x+En zéro
· 0lim0n
xx®= ; 0lim0x x®=.· 0
01 limx xx® >=+¥ ; 0 01 limx xx®· 2
0 01 limx xx® >=+¥ ; 2 0 01 limx xx® , n pairn xx® , n impairn xx® 1, n impairn xx® 1, n pairn xx®II) Polynômes
Etude à l'infini de 3f:2xxx+a et 3g:2xxx-a. Des études numériques avec des valeurs de x de plus en plus
grandes permettent d'obtenir :· limf()xx®+¥=+¥ avec
3limxx®+¥=+¥ et lim2xx®+¥=+¥.
· limg()xx®+¥=+¥ avec
3limxx®+¥=+¥ et lim2xx®+¥-=-¥.
Théorème : La limite en +o (ou en .o) d'un polynôme est donnée par la limite de son terme de plus haut degré. III) Fractions rationnelles : asymptotes verticale, horizontale et oblique
1) Etude à l'infini
a) ThéorèmeThéorème : la limite en +o (ou en .o) d'une fonction rationnelle est donnée par la limite du quotient de ses termes de plus haut degré.
b) Asymptote horizontale :Définition : Si limf()xxl®+¥=, alors la courbe représentative C f de f admet en +¥ la droite d'équation yl= comme asymptote horizontale.
Remarque : On a un énoncé analogue en -¥. yl=O lim()xfxl®-¥=1
C f1 C f2 lim()xfxl®+¥=2 lLimites et asymptotes 2/3
c) Asymptote oblique :Définition : Si []limf()()0x
x a xb®+¥-+=, alors la droite d'équation y a xb=+ est asymptote à la courbe représentative C f de f en +¥.Remarques :
f(x) peut alors s'écrire sous la forme f()()xaxbx=++j avec lim()0x x®+¥j=. On a un énoncé analogue en -¥.
2) Etude en un réel a borne de l'intervalle de définition
a) ThéorèmeThéorème : Soit f une fonction définie sur un intervalle de la forme ]a ; ...] (ou [... ; a[ ). Si la limite en a du numérateur est un réel non nul et si la limite du dénominateur est 0, alors la limite du quotient est infinie (le signe restant à
préciser). b) Asymptote verticaleDéfinition : Si on a limf()xax®=±¥, alors la courbe C f représentant la fonctio admet une asymptote verticale d'équation x = a.
IV) Théorèmes sur la limite d'une somme, d'un produit de deux fonctions.Dans tout ce paragraphe, f et g désignent deux fonctions dont on connaît, pour chacune, la limite " au même
endroit », soit en +¥, soit en -¥, soit en un réel a. l et l' désignent deux nombres réels.
Les théorèmes suivants permettent de conclure dans la plupart des cas ; les cas où l'on ne peut pas conclure
(appelés formes indéterminées) , sont signalés par . La méthode pour traiter ces cas plus difficiles est de
modifier l'écriture (forme factorisée " forme développée) pour changer de théorème à appliquer.
1) Théorème sur la limite d'une somme de deux fonctions
Si lim f est égale à l l l +¥ -¥ +¥ et lim g est égale à l' +¥ -¥ +¥ -¥ -¥ alors lim f + g est égale à l + l' +¥ -¥ +¥ -¥ ? ?
2) Théorème sur la limite d'un produit de deux fonctions
Si lim f est égale à l l ¹ 0 ±¥ 0 et lim g est égale à l' ±¥ ±¥ ±¥ alors lim fg est égale à ll' ±¥ ±¥ ? ?
C f baxy+=O )()(f)(baxxx+-=j
0)(®jx
xO x = a +¥=-®)(flimxax
C f -¥=+
®)(flimxaxC f
aLimites et asymptotes 3/3 V) Exemples
1) Soit f la fonction définie sur ]1 ; +¥[ par 21f()1x
xx+=-.· Limite en 1 : 2
1lim12x
x®+= et puisque 11lim10x
xx+ >-=, alors 2 1 11 lim1x xx x La droite d'équation x = 1 est asymptote verticale à C f .· Limite en +¥ : 22
· Asymptote oblique en +¥ : en montrant que 2f()11xxx=++-, on a2lim[f()(1)]lim01
xxxxx®+¥®+¥-+==- . La droite d'équation y = x + 1 est donc asymptote oblique à C f en +¥. Remarque : Le degré du numérateur est égal au degré du dénominateur + 1.2) Soit g la fonction définie sur R par 2
221g()1x
xx-=+.Limite en +¥ : 22
22212limlimlim221
x xxxx xx . La droite d'équation y = 2 est asymptote horizontale à C f en +¥.Remarques :
Le degré du numérateur est égal à celui du dénominateur. g(x) peut s'écrire g(x) sous la forme 2()x+j où lim()0x x®+¥j= : en effet 23g()21x x=-+.O y = x + 1 C f
O y = 2
C gquotesdbs_dbs47.pdfusesText_47[PDF] limite et continuité exercices
[PDF] limite et continuité exercices corrigés bac science
[PDF] limite et continuité pdf
[PDF] limite et continuité terminale s
[PDF] Limite et Factoriel
[PDF] Limite et image de fonction
[PDF] Limite et suite
[PDF] limite exponentielle en 0
[PDF] limite exponentielle et logarithme
[PDF] Limite finie de suite
[PDF] limite fonction
[PDF] limite fonction racine nième
[PDF] limite fonction rationnelle en 0
[PDF] limite fonction trigonométrique exercice corrigé
