Développements en séries entières usuels
retrouver les développements de nombreuses fonctions usuelles. L'exponentielle ln(1 + x) = +∞. ∑ n=1. (-1)n+1xn n pour
La fonction logarithme népérien
3 déc. 2014 Conclusion : la fonction ln est dérivable sur ]0; +∞[ et (ln x)′ = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...
fonctions-usuelles.pdf
pour limite +∞. Donc : lim x→+∞ lnx = +∞. 3. lim x→0. (lnx) = lim x→+∞ ln(. 1 x. ) (ln◦exp) (x) = ln exp(x) .exp (x) = 1. Paris Descartes. 2012 — 2013.
FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. −−−−−→ x→+∞. 0 x lnx −−−−−→ x→0+. 0 ln(x) x −1. −−−→ x→1. 1 ln(1+ x) x.
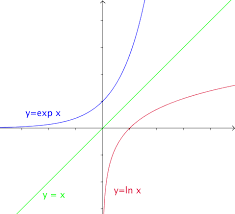FONCTION LOGARITHME NEPERIEN
Remarque : Les fonctions puissances imposent leur limite devant la fonction logarithme népérien. Propriétés : ( ). 0 ln 1 lim. 1 x x x. →. +. = Démonstration
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
Tableau des limites de ln et exponentielle
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? x?0+. 0 ln(x). Comparaison de la fonction logarithme avec la
Développements limités usuels
Développements limités usuels. Les développements limités ci-dessous sont ln(1 + x) = x→0 x − x2. 2. + ... + (−1)n−1 xn n. + o(xn) = x→0 n. ∑ k=1.
Fiche technique sur les limites
Comparaison de la fonction logarithme avec la fonction puissance en +∞ et en 0. En + ∞ lim x→+∞ ln(x) x. =
formulaire.pdf
lim x→+∞ ex/x = +∞ lim x→+∞ ln(x)/x = 0 lim x→−∞ xnex = 0 lim x→+∞ ex/xn = +∞ lim x→+∞ ln(x)/xn = 0. Dérivées. Fonctions usuelles Fonctions
formulaire.pdf
lim x??? xnex = 0 lim x?+? ex/xn = +? lim x?+? ln(x)/xn = 0. Dérivées. Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples.
FICHE : LIMITES ET ÉQUIVALENTS USUELS
Lycée Blaise Pascal. TSI 1 année. FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? x?0+. 0 ln(x).
Fiche technique sur les limites
Comparaison de la fonction logarithme avec la fonction puissance en +? et en 0. En + ? lim x?+? ln(x) x. =
Développements limités usuels
Développements limités usuels. Les développements limités ci-dessous sont valables quand x tend vers 0 et uniquement dans ce cas. ln(1 + x) =.
FONCTION LOGARITHME NEPERIEN
La fonction ln est continue sur 0;+????? donc pour tout réel a > 0
Exponentielle et logarithme
lim x??? ex = 0+ lim x?+? ex = +?. Fonction logarithme f(x) = ln(x) définie sur ]0; +? [ à valeurs dans R ln(1) = 0 ln(e)=1. (ln(x))? =.
I) Développements limités usuels
Tous les DL usuels suivants sont au voisinage de x = 0. Les développements limités se regroupent presque tous en deux familles. ln(1 + x) = x ?.
Développements limités usuels en 0
Développements limités usuels en 0 ln(1 ? x) = ?x ? ... II Fonctions usuelles. Fonction. Primitive. Intervalles ln x x(ln x ? 1). ] 0 ; +? [.
La fonction logarithme népérien
3 déc. 2014 Conclusion : la fonction ln est dérivable sur ]0; +?[ et (ln x)? = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...
Développements limités
développements limités des fonctions usuelles. FiGURe 5 – Fonction ln et ses polynômes de Taylor en 0 jusqu'à l'ordre n = 5.
Développements limités usuels
Les développements limités ci-dessous sont valables quandx tend vers 0et uniquement dans ce cas.
Formule deTaylor-Youngen0.f(x) =x→0n
k=0f (k)(0) k!xk+o(xn). ex=x→01+x+x22+...+xnn!+o(xn) =x→0n k=0x kk!+o(xn) chx=x→01+x22+...+x2n(2n)!+o(x2n) =x→0n
k=0x2k(2k)!+o(x2n) (et mêmeo(x2n+1)et mêmeO(x2n+2))
shx=x→0x+x36+...+x2n+1(2n+1)!+o(x2n+1) =x→0n
k=0x2k+1(2k+1)!+o(x2n+1) (et mêmeo(x2n+2)ouO(x2n+3))
cosx=x→01-x22+...+ (-1)nx2n(2n)!+o(x2n) =x→0n
k=0(-1)kx2k(2k)!+o(x2n) (et mêmeo(x2n+1)ouO(x2n+2)) sinx=x→0x-x36+...+ (-1)nx2n+1(2n+1)!+o(x2n+1) =x→0n
k=0(-1)kx2k+1(2k+1)!+o(x2n+1) (et mêmeo(x2n+2)ouO(x2n+3)) tanx=x→0x+x33+2x515+17x7315+o(x7)
11-x=x→01+x+x2+...+xn+o(xn) =x→0n
k=0x k+o(xn) 11+x=x→01-x+x2+...+ (-1)nxn+o(xn) =x→0n
k=0(-1)kxk+o(xn) ln(1+x) =x→0x-x22+...+ (-1)n-1xnn+o(xn) =x→0n
k=1(-1)k-1xkk+o(xn) ln(1-x) =x→0-x-x22+...-xnn+o(xn) =x→0-n?
k=1x kk+o(xn)Arctanx=x→0x-x3
3+...+ (-1)nx2n+12n+1+o(x2n+1) =x→0n
k=0(-1)kx2k+12k+1+o(x2n+1) (et mêmeo(x2n+2)ouO(x2n+3))Argthx=x→0x+x3
3+...+x2n+12n+1+o(x2n+1) =x→0n
k=0x2k+12k+1+o(x2n+1) (et mêmeo(x2n+2)ouO(x2n+3))
(1+x)α=x→01+αx+α(α-1)2x2+...+α(α-1)...(α- (n-1))n!xn+o(xn) (αréel donné)
x→0n k=0? k? x k+o(xn) 1 (1-x)2=x→01+2x+3x2+...(n+1)xn+o(xn) On obtient un développement de Arcsinx(resp. argshx) en intégrant un développement de1 ⎷1-x2= (1-x2)-1/2(resp. 1 ⎷1+x2= (1+x2)-1/2). c ?Jean-Louis Rouget, 2007. Tous droits réservés.1 http ://www.maths-france.frquotesdbs_dbs7.pdfusesText_5[PDF] limite logarithme népérien et exponentielle
[PDF] limite math
[PDF] limite math forme indéterminée
[PDF] limite math tableau
[PDF] limite polynome en 0
[PDF] limite polynome terme plus haut degré
[PDF] Limite quanx x tend vers +oo
[PDF] limite racine carré en 0
[PDF] limite racine carré forme indéterminée
[PDF] limite sinus en l'infini
[PDF] limite somme suite géométrique
[PDF] limite suite
[PDF] limite suite définie par récurrence
[PDF] limite suite géométrique
