 Développements en séries entières usuels
Développements en séries entières usuels
retrouver les développements de nombreuses fonctions usuelles. L'exponentielle ln(1 + x) = +∞. ∑ n=1. (-1)n+1xn n pour
 La fonction logarithme népérien
La fonction logarithme népérien
3 déc. 2014 Conclusion : la fonction ln est dérivable sur ]0; +∞[ et (ln x)′ = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...
 fonctions-usuelles.pdf
fonctions-usuelles.pdf
pour limite +∞. Donc : lim x→+∞ lnx = +∞. 3. lim x→0. (lnx) = lim x→+∞ ln(. 1 x. ) (ln◦exp) (x) = ln exp(x) .exp (x) = 1. Paris Descartes. 2012 — 2013.
 FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. −−−−−→ x→+∞. 0 x lnx −−−−−→ x→0+. 0 ln(x) x −1. −−−→ x→1. 1 ln(1+ x) x.
 FONCTION LOGARITHME NEPERIEN
FONCTION LOGARITHME NEPERIEN
Remarque : Les fonctions puissances imposent leur limite devant la fonction logarithme népérien. Propriétés : ( ). 0 ln 1 lim. 1 x x x. →. +. = Démonstration
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Tableau des limites de ln et exponentielle
Tableau des limites de ln et exponentielle
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? x?0+. 0 ln(x). Comparaison de la fonction logarithme avec la
 Développements limités usuels
Développements limités usuels
Développements limités usuels. Les développements limités ci-dessous sont ln(1 + x) = x→0 x − x2. 2. + ... + (−1)n−1 xn n. + o(xn) = x→0 n. ∑ k=1.
 Fiche technique sur les limites
Fiche technique sur les limites
Comparaison de la fonction logarithme avec la fonction puissance en +∞ et en 0. En + ∞ lim x→+∞ ln(x) x. =
 formulaire.pdf
formulaire.pdf
lim x→+∞ ex/x = +∞ lim x→+∞ ln(x)/x = 0 lim x→−∞ xnex = 0 lim x→+∞ ex/xn = +∞ lim x→+∞ ln(x)/xn = 0. Dérivées. Fonctions usuelles Fonctions
 formulaire.pdf
formulaire.pdf
lim x??? xnex = 0 lim x?+? ex/xn = +? lim x?+? ln(x)/xn = 0. Dérivées. Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples.
 FICHE : LIMITES ET ÉQUIVALENTS USUELS
FICHE : LIMITES ET ÉQUIVALENTS USUELS
Lycée Blaise Pascal. TSI 1 année. FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. ?????? x?+?. 0 x lnx ?????? x?0+. 0 ln(x).
 Fiche technique sur les limites
Fiche technique sur les limites
Comparaison de la fonction logarithme avec la fonction puissance en +? et en 0. En + ? lim x?+? ln(x) x. =
 Développements limités usuels
Développements limités usuels
Développements limités usuels. Les développements limités ci-dessous sont valables quand x tend vers 0 et uniquement dans ce cas. ln(1 + x) =.
 FONCTION LOGARITHME NEPERIEN
FONCTION LOGARITHME NEPERIEN
La fonction ln est continue sur 0;+????? donc pour tout réel a > 0
 Exponentielle et logarithme
Exponentielle et logarithme
lim x??? ex = 0+ lim x?+? ex = +?. Fonction logarithme f(x) = ln(x) définie sur ]0; +? [ à valeurs dans R ln(1) = 0 ln(e)=1. (ln(x))? =.
 I) Développements limités usuels
I) Développements limités usuels
Tous les DL usuels suivants sont au voisinage de x = 0. Les développements limités se regroupent presque tous en deux familles. ln(1 + x) = x ?.
 Développements limités usuels en 0
Développements limités usuels en 0
Développements limités usuels en 0 ln(1 ? x) = ?x ? ... II Fonctions usuelles. Fonction. Primitive. Intervalles ln x x(ln x ? 1). ] 0 ; +? [.
 La fonction logarithme népérien
La fonction logarithme népérien
3 déc. 2014 Conclusion : la fonction ln est dérivable sur ]0; +?[ et (ln x)? = 1 x . 3.2 Limite en 0 et en l'infini. Théorème 6 : On a les limites ...
 Développements limités
Développements limités
développements limités des fonctions usuelles. FiGURe 5 – Fonction ln et ses polynômes de Taylor en 0 jusqu'à l'ordre n = 5.
La fonction logarithme népérien
Table des matières
1 La fonction logarithme népérien2
1.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Représentation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.3 Variation de la fonction logarithme. . . . . . . . . . . . . . . . . . . 3
2 Propriétés de la fonction logarithme népérien4
2.1 Relation fonctionnelle. . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2 Quotient, inverse, puissance et racine carrée. . . . . . . . . . . . . . 4
3 Étude de la fonction logarithme népérien6
3.1 Dérivée. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.2 Limite en 0 et en l"infini. . . . . . . . . . . . . . . . . . . . . . . . . 6
3.3 Tableau de variation et courbe. . . . . . . . . . . . . . . . . . . . . . 7
3.4 Des limites de référence. . . . . . . . . . . . . . . . . . . . . . . . . 7
3.5 Dérivée de la fonction lnu. . . . . . . . . . . . . . . . . . . . . . . . 8
4 Applications9
4.1 Approximation de e. . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4.2 Étude d"une fonction. . . . . . . . . . . . . . . . . . . . . . . . . . . 9
5 Le logarithme décimal11
5.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
5.2 Applications. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
5.2.1 Nombre de chiffres dans l"écriture décimale. . . . . . . . . 12
5.2.2 En chimie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
5.2.3 En acoustique. . . . . . . . . . . . . . . . . . . . . . . . . . . 12
5.2.4 Papier semi-logarithmique et logarithmique. . . . . . . . . 14
PAULMILAN1 TERMINALES
TABLE DES MATIÈRES
Avant propos
La création de la fonction logarithme népérien est, à l"origine,antérieure à la fonction exponentielle bien que dans notre progression elle suive l"étude de la fonction exponentielle. La fonction logarithme a été créée par un drapier écossais du XVII esiècle. Ce drapier, Néper, cherche une fonction pour simplifierles longs calculs des astronomes, des navigateurs et des financiers. Il crée alors une fonc- tion qui transforme le produit en somme. C"est à dire quef(ab) =f(a)+f(b).Il a ensuite passé trente ans de sa vie à créer une table dite "de logarithmes» qui per- mettait d"effectuer les conversions nécessaires. C"est cette fonction, qui fait écho à la fonction exponentielle, qui est l"objet de ce chapitre.1 La fonction logarithme népérien
1.1 Définition
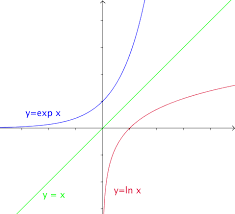
Définition 1 :On appelle fonction logarithme népérien notée ln, la fonction définie de]0;+∞[surRtelle que : x=ey?y=lnx On dit que la fonction ln est lafonction réciproquede la fonction exponentielle. Remarque :Cette fonction existe bien car la fonction exponentielle est une fonc- tion continue, strictement croissante à valeur dans]0;+∞[, donc d"après le théo- rème des valeurs intermédiaires l"équationx=ey, d"inconueyavecx?]0;+∞[, admet une unique solution lnx. ConséquenceOn a les relations suivantes : ln1=0 et lne=1 ainsi que : ?x?R, lnex=xet?x?]0;+∞[,elnx=x ?Faire attention aux ensembles de définition.1.2 Représentation
Théorème 1 :Les représentations de la fonction logarithme népérien et de la fonction exponentielle sont symétriques par rapport à la droite d"équationy=x. Démonstration :On noteClnetCexples courbes respectives des fonctions logarithme népérien et exponentielle.PAULMILAN2 TERMINALES
1. LA FONCTION LOGARITHME NÉPÉRIEN
Soit M(x;y)un point deClnavecx?]0;+∞[ety?R, doncy=lnx. On a alors x=ey, donc le point M"(y,x)est un point deCexp. Les courbesClnetCexpsont donc symétriques par rapport à la première bissectrice d"équationy=x. 12345-1 -2 -31 2 3 4 5 6-1-2-3 e e y=lnx y=ex xyyx M" M O
1.3 Variation de la fonction logarithme
Théorème 2 :La fonction ln est strictement croissante surR?+ Démonstration :Soit deux réelsaetbstrictement positifs etalna=0?a=1
lna lna<0?0 lna>0?a>1
Remarque :Ces propriétés permettent de résoudre des équations et des inéqua- tions. On veillera à mettre l"équation ou l"inéquation sous la forme ci-dessus et à déterminer les conditions de validité de l"équation ou de l"inéquation. PAULMILAN3 TERMINALES
TABLE DES MATIÈRES
Exemples :
Résoudre ln(2-2x) =1.
On met l"équation sous la forme : ln(2-2x) =lne l"équation est valide si, et seulement si, 2-2x>0 c"est à direx<1 On a alors :x<1 et 2-2x=esoitx=2-e
2 On a 2-e 2<1 car2-e2? -0,36.
On conclut alors :S=?2-e
2? Résoudre ln(2x+1)<-1
On met l"inéquation sous la forme : ln(2x+1)0 soitx>-1 2 On a alors :x>-1
2et 2x+1 On a :
e-1-1 2=1-e2e? -0,32 donc-12 On conclut par :S=?
-1 2;1-e2e?
2 Propriétés de la fonction logarithme népérien
2.1 Relation fonctionnelle
Théorème 3 :Pour tous réels strictement positifsaetb, on a : lnab=lna+lnb Démonstration :D"après les propriétés de l"exponentielle, on a : e a=eb?a=b Orelnab=abetelna+lnb=elna×elnb=ab
On conclut donc que lnab=lna+lnb.
Remarque :C"est cette propriété qui est à l"origine de la fonction logarithme. Exemple :ln2+ln3=ln6
2.2 Quotient, inverse, puissance et racine carrée
Théorème 4 :Pour tous réels strictement positifsaetb, on a : 1) ln a b=lna-lnb 2) ln 1 b=-lnb3) lnan=nlnaavecn?N 4) ln ⎷a=12lna PAULMILAN4 TERMINALES
2. PROPRIÉTÉS DE LA FONCTION LOGARITHME NÉPÉRIEN
Démonstration :
Pour démontrer la propriété 1, on revient aux propriétés de l"exponentielle. On aelna
b=abetelna-lnb=elnaelnb=abd"où la propriété : ln a b=lna-lnb Pour la deuxième propriété, on faita=1 La troisième propriété se démontre par récurrence à l"aide du produit. Pour la dernière propriété : on aa=⎷a×⎷adonc d"après la propriété du
produit, on a : lna=ln⎷ a+ln⎷a=2ln⎷ad"où ln⎷a=12lna Exemples :Voici 3 exemples d"utilisation de ces propriétés. Exprimer ln50 avec ln2 et ln5 et ln⎷12 avec ln2 et ln3 On a 50=2×52donc ln50=ln2+2ln5
On a 12=22×3 donc ln⎷
12=12(2ln2+ln3) =ln2+12ln3
Déterminer l"entierntel que 2n>10 000
On a donc : ln2
n>ln104soitnln2>4ln10 On obtient alors :n>4ln10
ln2or4ln10ln2?13.29 doncn?14 Résoudre l"équation : ln⎷2x-3=ln(6-x)-12lnx l"équation existe si ?2x-3>0 6-x>0 2 x<6 x>0 On en déduit l"ensemble de définition :Df=?3 2; 6? On a alors
1 2[ln(2x-3) +lnx] =ln(6-x)
soit lnx(2x-3) =2ln(6-x) L"équation revient à :
x?Dfetx(2x-3) = (6-x)2 2x2-3x=x2-12x+36
x 2+9x-36=0
On calcule :Δ=81+144=225=152on trouve alors deux solutions x ?=-9+15 2=3?Dfetx??=-9-152=-12 /?Df
on conclut par :S={3} PAULMILAN5 TERMINALES
TABLE DES MATIÈRES
3 Étude de la fonction logarithme népérien
3.1 Dérivée
Théorème 5 :La fonction logarithme népérien est dérivable sur]0;+∞[et : (lnx)?=1 x Démonstration :On admet que la fonction ln est continue sur]0;+∞[ On revient à la définition de la dérivée, c"est à dire on cherchelesa?]0;+∞[pour lesquels la limite suivante est finie : lim x→alnx-lna x-a Pour déterminer cette limite, on fait un changement de variable. Onpose alors X=lnxetA=lna. On a alorsx=eXeta=eAet six→a, comme la fonction ln est continue sur]0;+∞[, alorsX→lna. La limite devient alors : lim X→lnaX-A
eX-eA Or la fonction exponentielle est dérivable surRet la dérivée en lnaestelna: lim X→lnae
X-eA X-A=elna=a
Cette limite est strictement positive poura?]0;+∞[. On en déduit que la limite suivante existe pour touta?]0;+∞[et : lim X→lnaX-A
eX-eA=1a Conclusion : la fonction ln est dérivable sur]0;+∞[et(lnx)?=1 x. 3.2 Limite en 0 et en l"infini
Théorème 6 :On a les limites suivantes :
lim x→+∞lnx= +∞et limx→0+lnx=-∞ Démonstration :
Pour montrer la limite en+∞, on revient à la définition : Pour toutM>0, si lnx>Malors, comme la fonction exp est croissante, x>eM. Il existe donc un réelA=eMtel que six>Aalors lnx>M. Conclusion : lim
x→+∞lnx= +∞. PAULMILAN6 TERMINALES
3. ÉTUDE DE LA FONCTION LOGARITHME NÉPÉRIEN
Pour la deuxième limite, on fait un changement de variable. On poseX=1x. Donc six→0+alorsX→+∞. On a alors :
lim x→0+lnx=limX→+∞ln1 X=limX→+∞-lnX=-∞
3.3 Tableau de variation et courbe
On peut résumer les variations et les limites de la fonction ln, dans un tableau de variation : x 1 x ln 0+∞
1 0 e 1 On a alors la courbe représentative ci-
contre→ 12 -1 -2 -31 2 3 4 5 6 7 e y=lnx Oquotesdbs_dbs47.pdfusesText_47
lna<0?0 lna>0?a>1
Remarque :Ces propriétés permettent de résoudre des équations et des inéqua- tions. On veillera à mettre l"équation ou l"inéquation sous la forme ci-dessus et à déterminer les conditions de validité de l"équation ou de l"inéquation. PAULMILAN3 TERMINALES
TABLE DES MATIÈRES
Exemples :
Résoudre ln(2-2x) =1.
On met l"équation sous la forme : ln(2-2x) =lne l"équation est valide si, et seulement si, 2-2x>0 c"est à direx<1 On a alors :x<1 et 2-2x=esoitx=2-e
2 On a 2-e 2<1 car2-e2? -0,36.
On conclut alors :S=?2-e
2? Résoudre ln(2x+1)<-1
On met l"inéquation sous la forme : ln(2x+1)0 soitx>-1 2 On a alors :x>-1
2et 2x+1 On a :
e-1-1 2=1-e2e? -0,32 donc-12 On conclut par :S=?
-1 2;1-e2e?
2 Propriétés de la fonction logarithme népérien
2.1 Relation fonctionnelle
Théorème 3 :Pour tous réels strictement positifsaetb, on a : lnab=lna+lnb Démonstration :D"après les propriétés de l"exponentielle, on a : e a=eb?a=b Orelnab=abetelna+lnb=elna×elnb=ab
On conclut donc que lnab=lna+lnb.
Remarque :C"est cette propriété qui est à l"origine de la fonction logarithme. Exemple :ln2+ln3=ln6
2.2 Quotient, inverse, puissance et racine carrée
Théorème 4 :Pour tous réels strictement positifsaetb, on a : 1) ln a b=lna-lnb 2) ln 1 b=-lnb3) lnan=nlnaavecn?N 4) ln ⎷a=12lna PAULMILAN4 TERMINALES
2. PROPRIÉTÉS DE LA FONCTION LOGARITHME NÉPÉRIEN
Démonstration :
Pour démontrer la propriété 1, on revient aux propriétés de l"exponentielle. On aelna
b=abetelna-lnb=elnaelnb=abd"où la propriété : ln a b=lna-lnb Pour la deuxième propriété, on faita=1 La troisième propriété se démontre par récurrence à l"aide du produit. Pour la dernière propriété : on aa=⎷a×⎷adonc d"après la propriété du
produit, on a : lna=ln⎷ a+ln⎷a=2ln⎷ad"où ln⎷a=12lna Exemples :Voici 3 exemples d"utilisation de ces propriétés. Exprimer ln50 avec ln2 et ln5 et ln⎷12 avec ln2 et ln3 On a 50=2×52donc ln50=ln2+2ln5
On a 12=22×3 donc ln⎷
12=12(2ln2+ln3) =ln2+12ln3
Déterminer l"entierntel que 2n>10 000
On a donc : ln2
n>ln104soitnln2>4ln10 On obtient alors :n>4ln10
ln2or4ln10ln2?13.29 doncn?14 Résoudre l"équation : ln⎷2x-3=ln(6-x)-12lnx l"équation existe si ?2x-3>0 6-x>0 2 x<6 x>0 On en déduit l"ensemble de définition :Df=?3 2; 6? On a alors
1 2[ln(2x-3) +lnx] =ln(6-x)
soit lnx(2x-3) =2ln(6-x) L"équation revient à :
x?Dfetx(2x-3) = (6-x)2 2x2-3x=x2-12x+36
x 2+9x-36=0
On calcule :Δ=81+144=225=152on trouve alors deux solutions x ?=-9+15 2=3?Dfetx??=-9-152=-12 /?Df
on conclut par :S={3} PAULMILAN5 TERMINALES
TABLE DES MATIÈRES
3 Étude de la fonction logarithme népérien
3.1 Dérivée
Théorème 5 :La fonction logarithme népérien est dérivable sur]0;+∞[et : (lnx)?=1 x Démonstration :On admet que la fonction ln est continue sur]0;+∞[ On revient à la définition de la dérivée, c"est à dire on cherchelesa?]0;+∞[pour lesquels la limite suivante est finie : lim x→alnx-lna x-a Pour déterminer cette limite, on fait un changement de variable. Onpose alors X=lnxetA=lna. On a alorsx=eXeta=eAet six→a, comme la fonction ln est continue sur]0;+∞[, alorsX→lna. La limite devient alors : lim X→lnaX-A
eX-eA Or la fonction exponentielle est dérivable surRet la dérivée en lnaestelna: lim X→lnae
X-eA X-A=elna=a
Cette limite est strictement positive poura?]0;+∞[. On en déduit que la limite suivante existe pour touta?]0;+∞[et : lim X→lnaX-A
eX-eA=1a Conclusion : la fonction ln est dérivable sur]0;+∞[et(lnx)?=1 x. 3.2 Limite en 0 et en l"infini
Théorème 6 :On a les limites suivantes :
lim x→+∞lnx= +∞et limx→0+lnx=-∞ Démonstration :
Pour montrer la limite en+∞, on revient à la définition : Pour toutM>0, si lnx>Malors, comme la fonction exp est croissante, x>eM. Il existe donc un réelA=eMtel que six>Aalors lnx>M. Conclusion : lim
x→+∞lnx= +∞. PAULMILAN6 TERMINALES
3. ÉTUDE DE LA FONCTION LOGARITHME NÉPÉRIEN
Pour la deuxième limite, on fait un changement de variable. On poseX=1x. Donc six→0+alorsX→+∞. On a alors :
lim x→0+lnx=limX→+∞ln1 X=limX→+∞-lnX=-∞
3.3 Tableau de variation et courbe
On peut résumer les variations et les limites de la fonction ln, dans un tableau de variation : x 1 x ln 0+∞
1 0 e 1 On a alors la courbe représentative ci-
contre→ 12 -1 -2 -31 2 3 4 5 6 7 e y=lnx Oquotesdbs_dbs47.pdfusesText_47
lna>0?a>1
Remarque :Ces propriétés permettent de résoudre des équations et des inéqua- tions. On veillera à mettre l"équation ou l"inéquation sous la forme ci-dessus et à déterminer les conditions de validité de l"équation ou de l"inéquation.PAULMILAN3 TERMINALES
TABLE DES MATIÈRES
Exemples :
Résoudre ln(2-2x) =1.
On met l"équation sous la forme : ln(2-2x) =lne l"équation est valide si, et seulement si, 2-2x>0 c"est à direx<1On a alors :x<1 et 2-2x=esoitx=2-e
2 On a 2-e2<1 car2-e2? -0,36.
On conclut alors :S=?2-e
2?Résoudre ln(2x+1)<-1
On met l"inéquation sous la forme : ln(2x+1)On a alors :x>-1
2et 2x+1 On a :
e-1-1 2=1-e2e? -0,32 donc-12 On conclut par :S=?
-1 2;1-e2e?
2 Propriétés de la fonction logarithme népérien
2.1 Relation fonctionnelle
Théorème 3 :Pour tous réels strictement positifsaetb, on a : lnab=lna+lnb Démonstration :D"après les propriétés de l"exponentielle, on a : e a=eb?a=b Orelnab=abetelna+lnb=elna×elnb=ab
On conclut donc que lnab=lna+lnb.
Remarque :C"est cette propriété qui est à l"origine de la fonction logarithme. Exemple :ln2+ln3=ln6
2.2 Quotient, inverse, puissance et racine carrée
Théorème 4 :Pour tous réels strictement positifsaetb, on a : 1) ln a b=lna-lnb 2) ln 1 b=-lnb3) lnan=nlnaavecn?N 4) ln ⎷a=12lna PAULMILAN4 TERMINALES
2. PROPRIÉTÉS DE LA FONCTION LOGARITHME NÉPÉRIEN
Démonstration :
Pour démontrer la propriété 1, on revient aux propriétés de l"exponentielle. On aelna
b=abetelna-lnb=elnaelnb=abd"où la propriété : ln a b=lna-lnb Pour la deuxième propriété, on faita=1 La troisième propriété se démontre par récurrence à l"aide du produit. Pour la dernière propriété : on aa=⎷a×⎷adonc d"après la propriété du
produit, on a : lna=ln⎷ a+ln⎷a=2ln⎷ad"où ln⎷a=12lna Exemples :Voici 3 exemples d"utilisation de ces propriétés. Exprimer ln50 avec ln2 et ln5 et ln⎷12 avec ln2 et ln3 On a 50=2×52donc ln50=ln2+2ln5
On a 12=22×3 donc ln⎷
12=12(2ln2+ln3) =ln2+12ln3
Déterminer l"entierntel que 2n>10 000
On a donc : ln2
n>ln104soitnln2>4ln10 On obtient alors :n>4ln10
ln2or4ln10ln2?13.29 doncn?14 Résoudre l"équation : ln⎷2x-3=ln(6-x)-12lnx l"équation existe si ?2x-3>0 6-x>0 2 x<6 x>0 On en déduit l"ensemble de définition :Df=?3 2; 6? On a alors
1 2[ln(2x-3) +lnx] =ln(6-x)
soit lnx(2x-3) =2ln(6-x) L"équation revient à :
x?Dfetx(2x-3) = (6-x)2 2x2-3x=x2-12x+36
x 2+9x-36=0
On calcule :Δ=81+144=225=152on trouve alors deux solutions x ?=-9+15 2=3?Dfetx??=-9-152=-12 /?Df
on conclut par :S={3} PAULMILAN5 TERMINALES
TABLE DES MATIÈRES
3 Étude de la fonction logarithme népérien
3.1 Dérivée
Théorème 5 :La fonction logarithme népérien est dérivable sur]0;+∞[et : (lnx)?=1 x Démonstration :On admet que la fonction ln est continue sur]0;+∞[ On revient à la définition de la dérivée, c"est à dire on cherchelesa?]0;+∞[pour lesquels la limite suivante est finie : lim x→alnx-lna x-a Pour déterminer cette limite, on fait un changement de variable. Onpose alors X=lnxetA=lna. On a alorsx=eXeta=eAet six→a, comme la fonction ln est continue sur]0;+∞[, alorsX→lna. La limite devient alors : lim X→lnaX-A
eX-eA Or la fonction exponentielle est dérivable surRet la dérivée en lnaestelna: lim X→lnae
X-eA X-A=elna=a
Cette limite est strictement positive poura?]0;+∞[. On en déduit que la limite suivante existe pour touta?]0;+∞[et : lim X→lnaX-A
eX-eA=1a Conclusion : la fonction ln est dérivable sur]0;+∞[et(lnx)?=1 x. 3.2 Limite en 0 et en l"infini
Théorème 6 :On a les limites suivantes :
lim x→+∞lnx= +∞et limx→0+lnx=-∞ Démonstration :
Pour montrer la limite en+∞, on revient à la définition : Pour toutM>0, si lnx>Malors, comme la fonction exp est croissante, x>eM. Il existe donc un réelA=eMtel que six>Aalors lnx>M. Conclusion : lim
x→+∞lnx= +∞. PAULMILAN6 TERMINALES
3. ÉTUDE DE LA FONCTION LOGARITHME NÉPÉRIEN
Pour la deuxième limite, on fait un changement de variable. On poseX=1x. Donc six→0+alorsX→+∞. On a alors :
lim x→0+lnx=limX→+∞ln1 X=limX→+∞-lnX=-∞
3.3 Tableau de variation et courbe
On peut résumer les variations et les limites de la fonction ln, dans un tableau de variation : x 1 x ln 0+∞
1 0 e 1 On a alors la courbe représentative ci-
contre→ 12 -1 -2 -31 2 3 4 5 6 7 e y=lnx Oquotesdbs_dbs47.pdfusesText_47
On a :
e-1-12=1-e2e? -0,32 donc-12 On conclut par :S=?
-1 2;1-e2e?
2 Propriétés de la fonction logarithme népérien
2.1 Relation fonctionnelle
Théorème 3 :Pour tous réels strictement positifsaetb, on a : lnab=lna+lnb Démonstration :D"après les propriétés de l"exponentielle, on a : e a=eb?a=b Orelnab=abetelna+lnb=elna×elnb=ab
On conclut donc que lnab=lna+lnb.
Remarque :C"est cette propriété qui est à l"origine de la fonction logarithme. Exemple :ln2+ln3=ln6
2.2 Quotient, inverse, puissance et racine carrée
Théorème 4 :Pour tous réels strictement positifsaetb, on a : 1) ln a b=lna-lnb 2) ln 1 b=-lnb3) lnan=nlnaavecn?N 4) ln ⎷a=12lna PAULMILAN4 TERMINALES
2. PROPRIÉTÉS DE LA FONCTION LOGARITHME NÉPÉRIEN
Démonstration :
Pour démontrer la propriété 1, on revient aux propriétés de l"exponentielle. On aelna
b=abetelna-lnb=elnaelnb=abd"où la propriété : ln a b=lna-lnb Pour la deuxième propriété, on faita=1 La troisième propriété se démontre par récurrence à l"aide du produit. Pour la dernière propriété : on aa=⎷a×⎷adonc d"après la propriété du
produit, on a : lna=ln⎷ a+ln⎷a=2ln⎷ad"où ln⎷a=12lna Exemples :Voici 3 exemples d"utilisation de ces propriétés. Exprimer ln50 avec ln2 et ln5 et ln⎷12 avec ln2 et ln3 On a 50=2×52donc ln50=ln2+2ln5
On a 12=22×3 donc ln⎷
12=12(2ln2+ln3) =ln2+12ln3
Déterminer l"entierntel que 2n>10 000
On a donc : ln2
n>ln104soitnln2>4ln10 On obtient alors :n>4ln10
ln2or4ln10ln2?13.29 doncn?14 Résoudre l"équation : ln⎷2x-3=ln(6-x)-12lnx l"équation existe si ?2x-3>0 6-x>0 2 x<6 x>0 On en déduit l"ensemble de définition :Df=?3 2; 6? On a alors
1 2[ln(2x-3) +lnx] =ln(6-x)
soit lnx(2x-3) =2ln(6-x) L"équation revient à :
x?Dfetx(2x-3) = (6-x)2 2x2-3x=x2-12x+36
x 2+9x-36=0
On calcule :Δ=81+144=225=152on trouve alors deux solutions x ?=-9+15 2=3?Dfetx??=-9-152=-12 /?Df
on conclut par :S={3} PAULMILAN5 TERMINALES
TABLE DES MATIÈRES
3 Étude de la fonction logarithme népérien
3.1 Dérivée
Théorème 5 :La fonction logarithme népérien est dérivable sur]0;+∞[et : (lnx)?=1 x Démonstration :On admet que la fonction ln est continue sur]0;+∞[ On revient à la définition de la dérivée, c"est à dire on cherchelesa?]0;+∞[pour lesquels la limite suivante est finie : lim x→alnx-lna x-a Pour déterminer cette limite, on fait un changement de variable. Onpose alors X=lnxetA=lna. On a alorsx=eXeta=eAet six→a, comme la fonction ln est continue sur]0;+∞[, alorsX→lna. La limite devient alors : lim X→lnaX-A
eX-eA Or la fonction exponentielle est dérivable surRet la dérivée en lnaestelna: lim X→lnae
X-eA X-A=elna=a
Cette limite est strictement positive poura?]0;+∞[. On en déduit que la limite suivante existe pour touta?]0;+∞[et : lim X→lnaX-A
eX-eA=1a Conclusion : la fonction ln est dérivable sur]0;+∞[et(lnx)?=1 x. 3.2 Limite en 0 et en l"infini
Théorème 6 :On a les limites suivantes :
lim x→+∞lnx= +∞et limx→0+lnx=-∞ Démonstration :
Pour montrer la limite en+∞, on revient à la définition : Pour toutM>0, si lnx>Malors, comme la fonction exp est croissante, x>eM. Il existe donc un réelA=eMtel que six>Aalors lnx>M. Conclusion : lim
x→+∞lnx= +∞. PAULMILAN6 TERMINALES
3. ÉTUDE DE LA FONCTION LOGARITHME NÉPÉRIEN
Pour la deuxième limite, on fait un changement de variable. On poseX=1x. Donc six→0+alorsX→+∞. On a alors :
lim x→0+lnx=limX→+∞ln1 X=limX→+∞-lnX=-∞
3.3 Tableau de variation et courbe
On peut résumer les variations et les limites de la fonction ln, dans un tableau de variation : x 1 x ln 0+∞
1 0 e 1 On a alors la courbe représentative ci-
contre→ 12 -1 -2 -31 2 3 4 5 6 7 e y=lnx Oquotesdbs_dbs47.pdfusesText_47
On conclut par :S=?
-12;1-e2e?
2 Propriétés de la fonction logarithme népérien
2.1 Relation fonctionnelle
Théorème 3 :Pour tous réels strictement positifsaetb, on a : lnab=lna+lnb Démonstration :D"après les propriétés de l"exponentielle, on a : e a=eb?a=bOrelnab=abetelna+lnb=elna×elnb=ab
On conclut donc que lnab=lna+lnb.
Remarque :C"est cette propriété qui est à l"origine de la fonction logarithme.Exemple :ln2+ln3=ln6
2.2 Quotient, inverse, puissance et racine carrée
Théorème 4 :Pour tous réels strictement positifsaetb, on a : 1) ln a b=lna-lnb 2) ln 1 b=-lnb3) lnan=nlnaavecn?N 4) ln ⎷a=12lnaPAULMILAN4 TERMINALES
2. PROPRIÉTÉS DE LA FONCTION LOGARITHME NÉPÉRIEN
Démonstration :
Pour démontrer la propriété 1, on revient aux propriétés de l"exponentielle.On aelna
b=abetelna-lnb=elnaelnb=abd"où la propriété : ln a b=lna-lnb Pour la deuxième propriété, on faita=1 La troisième propriété se démontre par récurrence à l"aide du produit.Pour la dernière propriété : on aa=⎷a×⎷adonc d"après la propriété du
produit, on a : lna=ln⎷ a+ln⎷a=2ln⎷ad"où ln⎷a=12lna Exemples :Voici 3 exemples d"utilisation de ces propriétés. Exprimer ln50 avec ln2 et ln5 et ln⎷12 avec ln2 et ln3On a 50=2×52donc ln50=ln2+2ln5
On a 12=22×3 donc ln⎷
12=12(2ln2+ln3) =ln2+12ln3
Déterminer l"entierntel que 2n>10 000
On a donc : ln2
n>ln104soitnln2>4ln10On obtient alors :n>4ln10
ln2or4ln10ln2?13.29 doncn?14 Résoudre l"équation : ln⎷2x-3=ln(6-x)-12lnx l"équation existe si ?2x-3>0 6-x>0 2 x<6 x>0 On en déduit l"ensemble de définition :Df=?3 2; 6?On a alors
12[ln(2x-3) +lnx] =ln(6-x)
soit lnx(2x-3) =2ln(6-x)L"équation revient à :
x?Dfetx(2x-3) = (6-x)22x2-3x=x2-12x+36
x2+9x-36=0
On calcule :Δ=81+144=225=152on trouve alors deux solutions x ?=-9+152=3?Dfetx??=-9-152=-12 /?Df
on conclut par :S={3}PAULMILAN5 TERMINALES
TABLE DES MATIÈRES
3 Étude de la fonction logarithme népérien
3.1 Dérivée
Théorème 5 :La fonction logarithme népérien est dérivable sur]0;+∞[et : (lnx)?=1 x Démonstration :On admet que la fonction ln est continue sur]0;+∞[ On revient à la définition de la dérivée, c"est à dire on cherchelesa?]0;+∞[pour lesquels la limite suivante est finie : lim x→alnx-lna x-a Pour déterminer cette limite, on fait un changement de variable. Onpose alors X=lnxetA=lna. On a alorsx=eXeta=eAet six→a, comme la fonction ln est continue sur]0;+∞[, alorsX→lna. La limite devient alors : limX→lnaX-A
eX-eA Or la fonction exponentielle est dérivable surRet la dérivée en lnaestelna: limX→lnae
X-eAX-A=elna=a
Cette limite est strictement positive poura?]0;+∞[. On en déduit que la limite suivante existe pour touta?]0;+∞[et : limX→lnaX-A
eX-eA=1a Conclusion : la fonction ln est dérivable sur]0;+∞[et(lnx)?=1 x.3.2 Limite en 0 et en l"infini
Théorème 6 :On a les limites suivantes :
lim x→+∞lnx= +∞et limx→0+lnx=-∞Démonstration :
Pour montrer la limite en+∞, on revient à la définition : Pour toutM>0, si lnx>Malors, comme la fonction exp est croissante, x>eM. Il existe donc un réelA=eMtel que six>Aalors lnx>M.Conclusion : lim
x→+∞lnx= +∞.PAULMILAN6 TERMINALES
3. ÉTUDE DE LA FONCTION LOGARITHME NÉPÉRIEN
Pour la deuxième limite, on fait un changement de variable. On poseX=1x.Donc six→0+alorsX→+∞. On a alors :
lim x→0+lnx=limX→+∞ln1X=limX→+∞-lnX=-∞
3.3 Tableau de variation et courbe
On peut résumer les variations et les limites de la fonction ln, dans un tableau de variation : x 1 x ln0+∞
1 0 e 1On a alors la courbe représentative ci-
contre→ 12 -1 -2 -31 2 3 4 5 6 7 e y=lnx Oquotesdbs_dbs47.pdfusesText_47[PDF] limite logarithme népérien et exponentielle
[PDF] limite math
[PDF] limite math forme indéterminée
[PDF] limite math tableau
[PDF] limite polynome en 0
[PDF] limite polynome terme plus haut degré
[PDF] Limite quanx x tend vers +oo
[PDF] limite racine carré en 0
[PDF] limite racine carré forme indéterminée
[PDF] limite sinus en l'infini
[PDF] limite somme suite géométrique
[PDF] limite suite
[PDF] limite suite définie par récurrence
[PDF] limite suite géométrique
