 Fiche suites dintervention
Fiche suites dintervention
de douleurs abdominales lombaires ou des organes génitaux
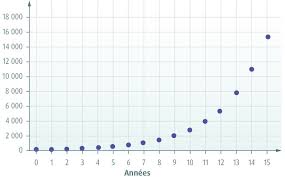 Terminale technologique - Suites numériques - Fiche de cours
Terminale technologique - Suites numériques - Fiche de cours
c. Définition d'une suite arithmétique. Une suite (un) est arithmétique s'il existe un nombre r tel que pour tout entier n on a : un+1=un+r.
 Terminale S
Terminale S
n'admet aucune limite. La suite est divergente. 3. Page 6. Fiches de Mathématiques. 1 SUITES.
 Fiche BAC 02 Terminale S Calcul des limites de Suites numériques
Fiche BAC 02 Terminale S Calcul des limites de Suites numériques
√n. Exercice n°2. 1 ère partie : On considère la suite définie par : u0=0 et pour tout entier n : un+1=√2un+3 a) A l'aide de votre calculatrice
 [PDF] suites arithmetiques et suites geometriques
[PDF] suites arithmetiques et suites geometriques
19 juin 2011 Si le premier terme est égal à 3 les premiers termes successifs sont : u0 = 3
 Fiche méthode : Suites Table des mati`eres 1 Rappel formules
Fiche méthode : Suites Table des mati`eres 1 Rappel formules
Fiche méthode : Suites. Table des mati`eres. 1 Rappel formules suites • S'il y a deux racines donc deux suites géométriques (vn) et (wn) vérifiant ...
 Terminale générale - Suites numériques - Fiche de cours
Terminale générale - Suites numériques - Fiche de cours
Fiche de cours. Terminale Générale - Mathématiques Spécialité - Année scolaire 2022/2023 https://physique-et-maths.fr. Page 3. 3/3. Suites numériques – Fiche de ...
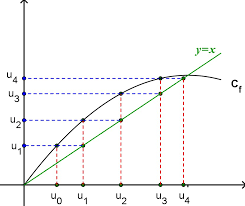 Fiche suites rappels de première S
Fiche suites rappels de première S
Terminale S. Page 2. 5 Suites arithmétique et géométrique. Suites arithmétiques. (utilisées pour des variations absolues). Suite géométriques. (utilisées pour
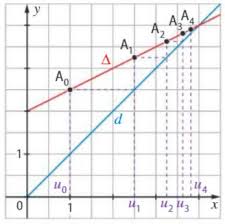 Terminale générale - Les suites - Fiche de cours
Terminale générale - Les suites - Fiche de cours
Limites de suite a. Définition. L'infini est un concept qui n'a pas d'équivalent physique ; il s'agit d'une limite. La limite d'une suite (un) est définie
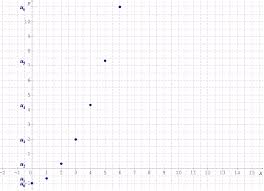 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
Suites numériques. LE COURS. [Série – Matière – (Option)]. 4. 3. Suites géométriques. Définition : Une suite u est dite géométrique s'il existe tel que pour
 Terminale S
Terminale S
Fiches de Mathématiques. 1 SUITES. Suites géométriques. ? Une suite (un) n? est géométrique s'il existe un réel q (la raison) indépendant de n tel que
 Fiche suites rappels de première S
Fiche suites rappels de première S
Fiche suites rappels de première S. 1 Définition. On peut définir une suite (un) : De façon explicite : un = f(n). De façon récurrente : à un terme :.
 Terminale générale - Suites numériques - Fiche de cours
Terminale générale - Suites numériques - Fiche de cours
Suites numériques – Fiche de cours. 1. Le raisonnement par récurrence. 2. Inégalité de Bernouilli. 3. Limite d'une suite. 3.1 Limite finie.
 Résumé du cours de mathématiques - ECS1 - Catherine
Résumé du cours de mathématiques - ECS1 - Catherine
Fiche 6. Ensemble des réels page 8. Fiche 7. Trigonométrie page 9. Fiche 8 Fiche 15. Fonctions trigonométriques page 17. Fiche 16. Suites usuelles.
 Fiche suites dintervention
Fiche suites dintervention
de douleurs abdominales lombaires ou des organes génitaux
 Fiche technique sur les limites
Fiche technique sur les limites
Fiche technique sur les limites. 1 Fonctions élémentaires. Les résultats suivants font +? ?? +? ??. F. Ind. Paul Milan. 1 sur 3. Terminale ES ...
 Cours de maths S/STI/ES - Suites et convergences
Cours de maths S/STI/ES - Suites et convergences
Terminale S/ES/STI. Mathématiques. Fiche n°2 - Suites et convergence. Suites et variations limite et convergence
 Fiche BAC 02 Terminale S Calcul des limites de Suites numériques
Fiche BAC 02 Terminale S Calcul des limites de Suites numériques
?n. Exercice n°2. 1 ère partie : On considère la suite définie par : u0=0 et pour tout entier n : un+1=?2un+3 a) A l'aide de votre calculatrice
 Fiche suites dintervention
Fiche suites dintervention
Si la cicatrice devient rouge chaude ou s'il existe une suréléva on de celle-ci
 Fiche suites dintervention
Fiche suites dintervention
Fiche suites d'intervention. Vous venez de subir une ou plusieurs instillation(s) endovésicale(s) d'Amétycine ® (Mitomycine C). Informations générales.
 [PDF] FICHE DE RÉVISION DU BAC - Studyrama
[PDF] FICHE DE RÉVISION DU BAC - Studyrama
Programme selon les sections : - notion de suite représentation graphique suites arithmétiques suites géométriques : toutes sections
 [PDF] COURS TERMINALE S LES SUITES NUMERIQUES - Frin Dominique
[PDF] COURS TERMINALE S LES SUITES NUMERIQUES - Frin Dominique
Les suites arithmétiques La suite (un) est une suite arithmétique s'il existe un nombre réel r tel que pour tout naturel n un+1 = un + r Le réel r est
 [PDF] Terminale S - Melusine
[PDF] Terminale S - Melusine
Fiches de Mathématiques 1 SUITES Suites géométriques ? Une suite (un) n? est géométrique s'il existe un réel q (la raison) indépendant de n tel que
 [PDF] Terminale générale - Suites numériques - Fiche de cours
[PDF] Terminale générale - Suites numériques - Fiche de cours
Suites numériques – Fiche de cours 1 Le raisonnement par récurrence Soit une propriété (Pn) définie sur ? ou un sous-ensemble de
 [PDF] Terminale générale - Les suites - Fiche de cours - Physique et Maths
[PDF] Terminale générale - Les suites - Fiche de cours - Physique et Maths
Les suites – Fiche de cours Mathématiques complémentaires Terminale Générale - Année scolaire 2020/2021 http s ://physique-et-maths fr
 [PDF] LES SUITES - maths et tiques
[PDF] LES SUITES - maths et tiques
Suites majorées minorées bornées - (un) est majorée s'il existe un réel M tel que pour tout n un ? M - (un) est minorée s'il existe un réel m tel que
 [PDF] SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES
[PDF] SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES
3) Représentation graphique Les points de la représentation graphique d'une suite arithmétique sont alignés Exemple : On a représenté ci-dessous la suite de
 [PDF] Cours de maths S/STI/ES - Suites et convergences
[PDF] Cours de maths S/STI/ES - Suites et convergences
Terminale S/ES/STI Mathématiques Fiche n°2 - Suites et convergence Suites et variations limite et convergence suites arithmétiques géométriques etc
 Suites - Cours - Fiches de révision - LEtudiant
Suites - Cours - Fiches de révision - LEtudiant
11 mar 2020 · Suites · 1 Suites arithmétiques · 2 Suites géométriques · 3 Limites de suites · 4 Convergences · 5 Suites adjacentes · 6 Suites arithmético-
 [PDF] Fiche suites rappels de première S - Lycée dAdultes
[PDF] Fiche suites rappels de première S - Lycée dAdultes
Fiche suites rappels de première S 1 Définition On peut définir une suite (un) : De façon explicite : un = f(n) De façon récurrente : à un terme :
Terminale S
Anne-Sophie PHILIPPE
BA CA 3A4A 2A 1 B 3B 4 B 2B 1 C 3 C 4C 2 C 1Table des matières
1 Suites2
1.1 Rappels sur les suites. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Suites arithmétiques et suites géométriques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.3 Démonstration par récurrence. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.4 Limite d"une suite. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.5 Suites adjacentes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Les fonctions6
2.1 Les limites d"une fonction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.2 Opérations sur les limites. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.3 Propriétés des limites. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.4 Continuité. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 8
2.5 Dérivation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 11
3 Fonction exponentielle et équation différentielle11
4 Fonction logarithme népérien12
5 Fonctions puissances et croissances comparées13
5.1 Fonctions puissancesxnet1xn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
5.2 Fonctions racinenième. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
5.3 Croissances comparées. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
5.4 Fonctions exponentielles de base. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
6 Les produits scalaires16
6.1 Produits scalaires dans le plan. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
6.2 Produits scalaires dans l"espace. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
7 Représentation analytique d"une droite de l"espace18
8 Les nombres complexes19
8.1 Introduction aux nombres complexes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
8.2 Calculs avec les nombres complexes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
8.3 Equation du second degré à coefficientsréels. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
8.4 Module et argument d"un nombre complexe. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
8.5 Propriétés du module et des arguments. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
8.6 Lien avec le plan complexe. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
8.7 Notation exponentielle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
8.8 Nombres complexes et transformations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
9 Intégration25
9.1 Intégration des fonctions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
9.2 Propriétés de l"intégrale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
9.3 Primitive. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 27
9.4 Intégrale et primitive. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
9.5 Intégration par parties. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
10 Les probabilités29
10.1 Introduction aux probabilités. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
10.2 Calculs de probabilités. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
10.3 Variable aléatoire. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Fiches de MathématiquesTABLE DES MATIÈRES
11 Dénombrement et lois de probabilité31
11.1 Dénombrement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31
11.2 Exemples de lois discrètes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
11.3 Lois de probabilité continue. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
12 Probabilités conditionnelles34
12.1 Les probabilités conditionnelles. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
12.2 Indépendance. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 34
1Fiches de Mathématiques1 SUITES
1 Suites
1.1 Rappels sur les suites
Variations d"une suite
?La suite(un)n??est croissante à partir du rangn0si et seulement si, pour toutn?n0,un+1?nn. ?La suite(un)n??est décroissante à partir du rangn0si et seulement si, pour toutn?n0,Un+1?Un. ?Une suite(un)n??est dite monotone si elle est croissante ou décroissante.Etude du sens de variation d"une suite
?Etude du signe deun+1-un. ?un=f(n), sifest monotone sur[0;+∞], alors la suite(un)n??est monotone, de même variation quef(formule explicite). ?Si(un)n??est strictement positive, on peut comparerun+1 unet 1. Si un+1 un>1,(un)n??est strictement croissante. Si un+1 un<1,(un)n??est strictement décroissante.Suites majorées, minorées, bornées...
?La suite(un)n??est majorée s"il existe un réelMtel que pour tout entiern,un?M. ?La suite(un)n??est minorée s"il existe un réelmtel que pour tout entiern,un?m. ?La suite(un)n??est bornée si elle est à la fois majorée et minorée.1.2 Suites arithmétiques et suites géométriques
Suites arithmétiques
?Une suite(un)n??est arithmétique s"il existe un réelr(la raison) indépendant dentel que, pour tout
n??, u n+1=un+r ?Pour tous entiersnetp,un=up+(n-p)×r. ?un=u0+n.r. ?limn→+∞un="+∞, sir>0 -∞, sir<0 ?Somme de termes consécutifs : (nombre de termes)×1erterme×dernier terme 2Exemple :
1+2+...+n=n×(n+1)2
2Fiches de Mathématiques1 SUITES
Suites géométriques
?Une suite(un)n??est géométrique s"il existe un réelq(la raison) indépendant dentel que, pour tout
n??, u n+1=un+q ?Pour tous entiersnetp,un=up×qn-q. ?un=u0×qn. ?limn→+∞qn="+∞, siq>10, si 0 ?Somme de termes consécutifs : (1ertermes)×1-qnombre de termes 1-q Exemple :
1+q1+q2+...+qn=1×1-qn+11-q
Attention : nombre de termes=n+1-1erterme
1.3 Démonstration par récurrence
Démonstration par récurrence
Pour démontrer que pour tout entiern?n0,Pn(proposition qui dépend den) est vraie, il faut : ?Initialisation: vérifier quePn0est vraie pourn0?0. ?Hypothèse de récurrence: considérer quePkest vraie pour un certain entierk?n0. ?Propriété d"hérédité: démontrer quePn+1est vraie. ?Conclusion: pour toutn?n0,Pnest vraie. 1.4 Limite d"une suite
Limites d"une suite numérique(un)n??
?La suite(un)n??converge vers un réel?. Ceci signifie que tout intervalle contenant?contient aussi
tous les termes de la suite à partir d"un certain rangp. lim n→+∞un=? (un)n??est convergente et converge vers?. ?La suite(un)n??a pour limite+∞. Cela signifie que tout intervalle ouvert]A;+∞[contient tous les
termes de la suite à partir d"un certain rangp. La suite est divergente. ?La suite(un)n??a pour limite-∞. Ceci signifie que tout intervalle ouvert]-∞;B[contient tous les
termes de la suite à partir d"un certain rangp. La suite est divergente. ?La suite(un)n??n"admet aucune limite. La suite est divergente. 3 Fiches de Mathématiques1 SUITES
Suites monotones
?Si une suite(un)n??est croissante et non majorée, alors : lim n→+∞un=+∞ ?Si une suite(un)n??est décroissante et non minorée, alors : lim n→+∞un=-∞ ?Une suite croissante et majorée est convergente. ?Une suite décroissante et minorée est convergente. ROC 1 : limite d"une suite croissante non majorée ?La suite(un)n??n"est pas majorée : quelque soit le réelA, on peut trouver un entierptel queup?A.
?La suite(un)n??est croissante. Pour toutn?p:#un?up u n>A. ?A partir du rangp, tous les termes de la suite sont dans]A;+∞[. ?Conclusion : par définition, cela prouve : lim n→+∞un=+∞ ROC 2 : limite d"une suite décroissante non minorée ?La suite(un)n??n"est pas minorée : quelque soit le réelB, on peut trouver un entierptel queup?B
?La suite(un)n??est décroissante. Pour toutn?p:#un?up u n?Soit la suite(un)n??, croissante et majorée par un réelM. NotonsA, le plus petit des majorants. ?Tout intervalle]A-α;A+α[contient au moins un termeupde la suite. Sinon,A-αserait un majorant de la suite, ce qui contredit le fait queAsoit le plus petit des majorants. ?La suite(un)n??est croissante : pour toutn?p,un?up. ?Conclusion: l"intervalle]A-α;A+α[contient tous les termes de la suite à partir du rangp. Ceci
est vrai, quel que soit le réelα >0. Par définition, la suite(un)n??converge et à pour limiteA. 4 Fiches de Mathématiques1 SUITES
ROC 4 : limite d"une suite décroissante et minorée ?Soit la suite(un)n??décroissante et minorée par un réelm. NotonsB, le plus grand des minorants.
?Tout intervalle]B-α;B+α[contient au moins un termeupde la suite. Sinon,B+αserait un minorant de la suite, ce qui contredit le fait queBsoit le plus grand des minorants. ?La suite(un)n??est décroissante : pour toutn?p,un?up. ?Conclusion: l"intervalle]B-α;B+α[contient tous les termes de la suite à partir du rangp. Ceci
est vrai, quelque soit le réelα >0. Par définition, la suite(un)n??converge et à pour limiteB. Limite d"une suite géométrique
?Soit(un)n??, une suite géométrique de raisonqnon nulle. Pour tout entiern:
un=u0×qn ?Si|q|<1, limn→+∞qn=0 ?Siq>1, limn→+∞qn= +∞ ?Siq=1, limn→+∞qn=1 ?Siq?-1,qnn"a pas de limite. Théorème d"encadrement (" des gendarmes ») Soient trois suites(un)n??,(vn)n??,(wn)n??telles que : ?n?n0,v n?un?wnlimn→+∞vn=? lim n→+∞wn=???? limn→+∞un=? 1.5 Suites adjacentes
Théorème et définition
Deux suites(un)n??et(vn)n??sont adjacentes si et seulement si : ?(un)n??est croissante. ?(un)n??est décroissante. ?limn→+∞un-vn=0 Théorème: Si deux suites sont adjacentes alors elles convergent et elles ont la même limite.
5 Fiches de Mathématiques2 LES FONCTIONS
2 Les fonctions
2.1 Les limites d"une fonction
Définitions
?Limite finie d"une fonction en+ou-∞: présence d"une assymptote horizontale (d"équationy=?)
à?fen+ou-∞.
lim x→+∞1 xn=0 lim x→+∞1 ?x=0 ?Limite infinie d"une fonction à l"infini. Pas d"assymptote. lim x→+∞xn= +∞ lim x→+∞? x=+∞ lim x→-∞xn= +∞(npair) lim x→+∞xn=-∞(nimpair) ?Cas particulier : limx→+∞f(x)-(ax+b)=0 La droite d"équationy=ax+best assymptote oblique à?fen+∞. ?Limite def(x)quandxtend versaen+∞: présence d"une assymptote verticale (x=a) à?f. lim x→0+1 xn=lim x→0-1xn=+∞(npair) lim x→0+1 xn= +∞et lim x→0-1xn=-∞(nimpair) ?Limite finie de la fonction en un réela. limx→af(x)=? 6 Fiches de Mathématiques2 LES FONCTIONS
2.2 Opérations sur les limites
Formes indéterminées
limx→αf=+∞ lim x→αg=-∞??? limx→αf+gest indéterminée lim x→αf=±∞ lim x→αg=0??? limx→αf×gest indéterminée lim x→αf=±∞ lim x→αg=±∞??? limx→αf gest indéterminée lim x→αf=0 lim x→αg=0??? limx→αf gest indéterminée Limite d"une fonction polynôme ou d"une fonction rationnelle ?Règle 1: en±∞, la limite d"une fonction polynôme est égale à la limite de son terme de plus haut
degré. ?Règle 2: en±∞, la limite d"une fonction rationnelle (quotient de deux polynômes) est égale à la
limite du quotient du terme de plus haut degré du numérateur par le terme de plus haut degré du
dénominateur. Composé de deux fonctions
On notef, la composé deusuivie dev:
f=v◦u lim x→au(x)=b lim x→bv(x)=c??? limx→av◦u(x)=c Remarque: vérifier les domaines de définition.u, définie sur l"intervalleIetvdéfinie sur l"intervalle
Jtel que :?x?I,u(x)?J
2.3 Propriétés des limites
Unicité
Sifadmet une limite enα, alors, cette limite est unique. 7 Fiches de Mathématiques2 LES FONCTIONS
Théorèmes de comparaison
?Théorème 1: au voisinage deα, Sif(x)?u(x)et limx→αu(x)=+∞, alors, limx→αf(x) =+∞(1) Sif(x)?v(x)et limx→αu(x)=-∞, alors, limx→αf(x)=-∞(2) ?Démonstrations (ROC) (1) Soit,α=+∞. Tout intervalle]M;+∞[, oùMest un réel, contient touslesu(x)pourxassezgrand.
Or, au voisinage deα,f(x)?u(x). Donc, pourxassez grand, tous lesf(x)sont contenus dans ]M;+∞[. Par définition,
limx→+∞f(x)= +∞ (2) Idem ?Théorème 2: au voisinage deα, Si limx→α|f(x)-?|?u(x)et limx→αu(x)=0 Alors, lim
x→αf(x) =?. ?Théorème 3 : Théorème des gendarmes: au voisinage deα Siu(x)?f(x)?v(x)et limx→αu(x)=limx→αv(x) =?, alors, lim x→αf(x)=?. ?Démonstration (ROC) Soit,α=+∞.
Pourx>A:u(x)?f(x)?v(x)
limx→+∞u(x)=?signifie que pourx>B,u(x)?IavecIintervalle contenant?. lim x→+∞v(x)=?signifie que pourx>C,v(x)?I. PrenonsMle plus grand des nombresA,B,C.
?x?M,on a???u(x)?f(x)?v(x) u(x)?I v(x)?I Doncf(x)?I.
Par définition, limx→+∞f(x)=?.
?Comptabilité avec l"ordre Au voisinage deα: sif(x)?g(x)et limx→αf(x)=?et limx→αg(x)=?? Alors,????
2.4 Continuité
Définitions et théorèmes
?Sifest continue ena: lim x→a-f(x)=lim x→a+f(x) =f(a) ?Sifest dérivable ena?I, alorsfest continue ena. ?Sifest dérivable surI, alorsfest continue surI. Remarque: la réciproque est fausse, une fonction continue n"est pas toujours dérivable. 8 Fiches de Mathématiques2 LES FONCTIONS
Démonstration (ROC) toute fonction dérivable est continue fest dérivable enasignifie que, limx→af(x)-f(a)x-a=f?(a) Soitg, la fonction définie sur un voisinage deapar : g(x)=f(x)-f(a) x-a avecx?=a f(x) =(x-a)×g(x)+f(a) lim x→ax-a=0 et limx→ag(x)=f?(a) Donc lim
x→af(x)=f(a) Par définition,fest continue ena.
Cas particuliers
?Les fonctions polynômes sont continues sur?. ?Les fonctions rationnelles sont continues sur chacun des intervalles du domaine de définition. ?Les fonctions sinus et cosinus sont continues sur? ?Toutefonctionconstruite paraddition,multiplicationoucompositionde fonctionscontinuesestune fonction continue. ?La fonction racine carrée est définie sur[0;+∞[et est dérivable sur]0;+∞[. Selon le théorème, cette fonction est continue sur]0;+∞[. Mais, sa limite en 0 est 0 donc elle est continue sur[0;+∞[. 9 Fiches de Mathématiques2 LES FONCTIONS
Nombre dérivé
lim h→0f(a+h)-f(a)h=? f(a+h)=f(a)+?h+h?(h)avec lim h→0?(h)=0 Si ces propositions sont vraies,fest dérivable enaet?est le nombre dérivé defenanotéf?(a).
Sifest dérivable ena, la courbe?fadmet au pointA(a;f(a))une tangente?dont le coefficient directeur estf?(a). L"équation de?est : y=f?(a)×(x-a)+f(a) Si la limite du taux d"accroissement entreaeta+hdefest±∞, alorsfn"est pas dérivable. Il y a pas
de tangente verticale ena. Si les limites sont différentes à droite et à gauche, alorsfn"est pas dérivable ena. Il y a un point
anguleux ena. Théorème des valeurs intermédiaires
Sifest continue sur[a;b], alors, pour tout réelkcompris entref(a)etf(b), il existe au moins un réelcappartenant à[a;b]tel que f(c) =k. L"équationf(x)=kadmet au moins une solution dans[a;b]. Théorème de bijection ou corollaire du theorème des valeursintermédiaires Sifest continue et strictement croissante sur[a;b],f([a;b]) =[f(a);f(b)]. Alors,
?y?[f(a);f(b)], il existe un et un seul réelc?[a;b]tel quef(c) =y. L"équationf(x)=yadmet une et une seule solution dans[a;b]. Idem pour une fonction strictement décroissante.f([a;b]) =[f(b);f(a)]. Toute fonction continue et strictement monotone sur un intervalle donné réalise une bijection...
Démonstration (ROC)
?Supposonsfcontinue et strictement croissante sur[a;b]. ?Existence : fest continue sur[a;b]. D"après le théorème des valeurs intermédiaires,?y?[f(a);f(b)], l"équation
f(x)=yadmet au moins une solution. ?Unicité : Supposons quef(c1) =f(c2) =yavecc1 Cela contredit la suppositionf(c1)=f(c2)=y.
Donc, il existe un seul réelctel quef(c) =y.
10 Fiches de Mathématiques3 FONCTION EXPONENTIELLE ET ÉQUATION DIFFÉRENTIELLE 2.5 Dérivation
Rappels
?fest constante si et seulement sif?est nulle. ?fest croissante si et seulement sif?est positive. ?fest décroissante si et seulement sif?est négative. ?Sif(a)est un extremum local defenaalors,f?(a) =0. (réciproque fausse) ?Sif?s"annule et change de signe enaalors,f(a)est un extremum local. Dérivée d"une fonction composée
gdérivable surJetudérivable surItels que :?x?I,u(x)?J. Alors,f=g◦uest dérivable surIet on a(g◦u)?(x)=g?(u(x))×u?(x) (g◦u)?= (g?◦u)×u? Exemples importants
u, fonction positive et dérivable surI. ?f=? uest dérivable et donne :(?u)?=u?2?u. ?f=unest dérivable et donne :(un)?=n×un-1×u? 3 Fonction exponentielle et équation différentielle
Définition
On dit quef, fonction dérivable sur un intervalleI, est solution de l"équation différentielley?=k.y,
lorsque?x?I,f?(x) =k.f(x). Fonction exponentielle
Il existeune et une seule fonctiondérivable sur?telle quey?=yety(0)=1 (condition initiale). C"est la
fonction exponentielle. ?(exp)?=exp?ea+b=ea×eb ?e2a= [ea]2?e-a=1 ea ?ea-b=ea eb?(ea)n=en.a ?e0=1 ?La fonction exponentielle est strictement croissante sur? ?limx→+∞ex= +∞et limx→-∞ex=0 ?lim h→0e h-1 h=1 ?limx→+∞e x x=+∞et limx→-∞x.ex=0 ?limx→+∞e x xn=+∞et limx→-∞xn.ex=0 ?Fonction composéeeu.(eu)?=u?.eu 11 Fiches de Mathématiques4 FONCTION LOGARITHME NÉPÉRIEN Equationy?=a.y
L"ensemble des solutions dans?de l"équationy?=ayest l"ensemble des fonctions x?→c.eax oùcest un réel quelconque. Il existeune unique solutionvérifiant la condition initialey?(x0) =y0. Equationy?=ay+b
Les solutions de l"équation(E):y?=a.y+bsont les fonctions définies sur?, de la formef-baoùf est solution dey?=ay. C"est-à-dire x?→Ceax-b a oùC??. Siy(x0) =y0,(E)admetune uniquesolution. 4 Fonction logarithme népérien
Propriétés
?ln(1) =0?ln(e)=1 ?eln(a)=a?ln(ea) =a ?ln(a×b)=ln(a)+ln(b)?lna b=ln(a)-ln(b) ?ln1 a=-ln(a)?ln?a=12ln(a) ?ln(an)=n×ln(a) Etude de la fonction
?La fonction ln est définie et continue sur]0;+∞[. ? ?x?]0;+∞[, ln?(x)=1 x. ?La fonction ln est croissante sur]0;+∞[. ?limx→+∞ln(x)=+∞et limx→0ln(x)=-∞ ?limx→+∞ln(x) x=0 et limx→0x.ln(x)=0 ?limx→1ln(x) x-1=1 et limx→0ln(x+1)x=1 12 Fiches de Mathématiques5 FONCTIONS PUISSANCES ET CROISSANCES COMPARÉES Démonstration (ROC)
Soita>0, démontrons que lim
h→0ln(a+h)-ln(a)h=1aou limx→0ln(a)-ln(x)a-x=1a. PosonsA=ln(a),a=eAetX=ln(x),x=eX.
ln(a)-ln(x) a-x=A-XeA-eX=1eA-eX A-X. Comme ln est continue sur]0;+∞[, limx→aln(x)=ln(a). lim X→ln(a)e
A-eX A-X=limX→Ae
A-eXA-X=exp?(A) =exp(A) =exp(ln(a)) =a.
lim x→aln(a)-ln(x) a-x=limX→A1eA-eX A-X=1a.
D"où ln est dérivable ena>0 et ln?(a)=1
a. Fonctionln◦u
(ln◦u)?(x) =u?(x)u(x)quotesdbs_dbs41.pdfusesText_41
Exemple :
1+q1+q2+...+qn=1×1-qn+11-q
Attention : nombre de termes=n+1-1erterme
1.3 Démonstration par récurrence
Démonstration par récurrence
Pour démontrer que pour tout entiern?n0,Pn(proposition qui dépend den) est vraie, il faut : ?Initialisation: vérifier quePn0est vraie pourn0?0. ?Hypothèse de récurrence: considérer quePkest vraie pour un certain entierk?n0. ?Propriété d"hérédité: démontrer quePn+1est vraie. ?Conclusion: pour toutn?n0,Pnest vraie.1.4 Limite d"une suite
Limites d"une suite numérique(un)n??
?La suite(un)n??converge vers un réel?. Ceci signifie que tout intervalle contenant?contient aussi
tous les termes de la suite à partir d"un certain rangp. lim n→+∞un=? (un)n??est convergente et converge vers?.?La suite(un)n??a pour limite+∞. Cela signifie que tout intervalle ouvert]A;+∞[contient tous les
termes de la suite à partir d"un certain rangp. La suite est divergente.?La suite(un)n??a pour limite-∞. Ceci signifie que tout intervalle ouvert]-∞;B[contient tous les
termes de la suite à partir d"un certain rangp. La suite est divergente. ?La suite(un)n??n"admet aucune limite. La suite est divergente. 3Fiches de Mathématiques1 SUITES
Suites monotones
?Si une suite(un)n??est croissante et non majorée, alors : lim n→+∞un=+∞ ?Si une suite(un)n??est décroissante et non minorée, alors : lim n→+∞un=-∞ ?Une suite croissante et majorée est convergente. ?Une suite décroissante et minorée est convergente. ROC 1 : limite d"une suite croissante non majorée?La suite(un)n??n"est pas majorée : quelque soit le réelA, on peut trouver un entierptel queup?A.
?La suite(un)n??est croissante. Pour toutn?p:#un?up u n>A. ?A partir du rangp, tous les termes de la suite sont dans]A;+∞[. ?Conclusion : par définition, cela prouve : lim n→+∞un=+∞ ROC 2 : limite d"une suite décroissante non minorée?La suite(un)n??n"est pas minorée : quelque soit le réelB, on peut trouver un entierptel queup?B
?La suite(un)n??est décroissante. Pour toutn?p:#un?up u n?Conclusion: l"intervalle]A-α;A+α[contient tous les termes de la suite à partir du rangp. Ceci
est vrai, quel que soit le réelα >0. Par définition, la suite(un)n??converge et à pour limiteA. 4Fiches de Mathématiques1 SUITES
ROC 4 : limite d"une suite décroissante et minorée?Soit la suite(un)n??décroissante et minorée par un réelm. NotonsB, le plus grand des minorants.
?Tout intervalle]B-α;B+α[contient au moins un termeupde la suite. Sinon,B+αserait un minorant de la suite, ce qui contredit le fait queBsoit le plus grand des minorants. ?La suite(un)n??est décroissante : pour toutn?p,un?up.?Conclusion: l"intervalle]B-α;B+α[contient tous les termes de la suite à partir du rangp. Ceci
est vrai, quelque soit le réelα >0. Par définition, la suite(un)n??converge et à pour limiteB.Limite d"une suite géométrique
?Soit(un)n??, une suite géométrique de raisonqnon nulle.Pour tout entiern:
un=u0×qn ?Si|q|<1, limn→+∞qn=0 ?Siq>1, limn→+∞qn= +∞ ?Siq=1, limn→+∞qn=1 ?Siq?-1,qnn"a pas de limite. Théorème d"encadrement (" des gendarmes ») Soient trois suites(un)n??,(vn)n??,(wn)n??telles que : ?n?n0,v n?un?wnlimn→+∞vn=? lim n→+∞wn=???? limn→+∞un=?1.5 Suites adjacentes
Théorème et définition
Deux suites(un)n??et(vn)n??sont adjacentes si et seulement si : ?(un)n??est croissante. ?(un)n??est décroissante. ?limn→+∞un-vn=0Théorème: Si deux suites sont adjacentes alors elles convergent et elles ont la même limite.
5Fiches de Mathématiques2 LES FONCTIONS
2 Les fonctions
2.1 Les limites d"une fonction
Définitions
?Limite finie d"une fonction en+ou-∞: présence d"une assymptote horizontale (d"équationy=?)
à?fen+ou-∞.
lim x→+∞1 xn=0 lim x→+∞1 ?x=0 ?Limite infinie d"une fonction à l"infini. Pas d"assymptote. lim x→+∞xn= +∞ lim x→+∞? x=+∞ lim x→-∞xn= +∞(npair) lim x→+∞xn=-∞(nimpair) ?Cas particulier : limx→+∞f(x)-(ax+b)=0 La droite d"équationy=ax+best assymptote oblique à?fen+∞. ?Limite def(x)quandxtend versaen+∞: présence d"une assymptote verticale (x=a) à?f. lim x→0+1 xn=lim x→0-1xn=+∞(npair) lim x→0+1 xn= +∞et lim x→0-1xn=-∞(nimpair) ?Limite finie de la fonction en un réela. limx→af(x)=? 6Fiches de Mathématiques2 LES FONCTIONS
2.2 Opérations sur les limites
Formes indéterminées
limx→αf=+∞ lim x→αg=-∞??? limx→αf+gest indéterminée lim x→αf=±∞ lim x→αg=0??? limx→αf×gest indéterminée lim x→αf=±∞ lim x→αg=±∞??? limx→αf gest indéterminée lim x→αf=0 lim x→αg=0??? limx→αf gest indéterminée Limite d"une fonction polynôme ou d"une fonction rationnelle?Règle 1: en±∞, la limite d"une fonction polynôme est égale à la limite de son terme de plus haut
degré.?Règle 2: en±∞, la limite d"une fonction rationnelle (quotient de deux polynômes) est égale à la
limite du quotient du terme de plus haut degré du numérateur par le terme de plus haut degré du
dénominateur.Composé de deux fonctions
On notef, la composé deusuivie dev:
f=v◦u lim x→au(x)=b lim x→bv(x)=c??? limx→av◦u(x)=cRemarque: vérifier les domaines de définition.u, définie sur l"intervalleIetvdéfinie sur l"intervalle
Jtel que :?x?I,u(x)?J
2.3 Propriétés des limites
Unicité
Sifadmet une limite enα, alors, cette limite est unique. 7Fiches de Mathématiques2 LES FONCTIONS
Théorèmes de comparaison
?Théorème 1: au voisinage deα, Sif(x)?u(x)et limx→αu(x)=+∞, alors, limx→αf(x) =+∞(1) Sif(x)?v(x)et limx→αu(x)=-∞, alors, limx→αf(x)=-∞(2) ?Démonstrations (ROC)(1) Soit,α=+∞. Tout intervalle]M;+∞[, oùMest un réel, contient touslesu(x)pourxassezgrand.
Or, au voisinage deα,f(x)?u(x). Donc, pourxassez grand, tous lesf(x)sont contenus dans ]M;+∞[.Par définition,
limx→+∞f(x)= +∞ (2) Idem ?Théorème 2: au voisinage deα, Si limx→α|f(x)-?|?u(x)et limx→αu(x)=0Alors, lim
x→αf(x) =?. ?Théorème 3 : Théorème des gendarmes: au voisinage deα Siu(x)?f(x)?v(x)et limx→αu(x)=limx→αv(x) =?, alors, lim x→αf(x)=?. ?Démonstration (ROC)Soit,α=+∞.
Pourx>A:u(x)?f(x)?v(x)
limx→+∞u(x)=?signifie que pourx>B,u(x)?IavecIintervalle contenant?. lim x→+∞v(x)=?signifie que pourx>C,v(x)?I.PrenonsMle plus grand des nombresA,B,C.
?x?M,on a???u(x)?f(x)?v(x) u(x)?I v(x)?IDoncf(x)?I.
Par définition, limx→+∞f(x)=?.
?Comptabilité avec l"ordre Au voisinage deα: sif(x)?g(x)et limx→αf(x)=?et limx→αg(x)=??Alors,????
2.4 Continuité
Définitions et théorèmes
?Sifest continue ena: lim x→a-f(x)=lim x→a+f(x) =f(a) ?Sifest dérivable ena?I, alorsfest continue ena. ?Sifest dérivable surI, alorsfest continue surI. Remarque: la réciproque est fausse, une fonction continue n"est pas toujours dérivable. 8Fiches de Mathématiques2 LES FONCTIONS
Démonstration (ROC) toute fonction dérivable est continue fest dérivable enasignifie que, limx→af(x)-f(a)x-a=f?(a) Soitg, la fonction définie sur un voisinage deapar : g(x)=f(x)-f(a) x-a avecx?=a f(x) =(x-a)×g(x)+f(a) lim x→ax-a=0 et limx→ag(x)=f?(a)Donc lim
x→af(x)=f(a)Par définition,fest continue ena.
Cas particuliers
?Les fonctions polynômes sont continues sur?. ?Les fonctions rationnelles sont continues sur chacun des intervalles du domaine de définition. ?Les fonctions sinus et cosinus sont continues sur? ?Toutefonctionconstruite paraddition,multiplicationoucompositionde fonctionscontinuesestune fonction continue. ?La fonction racine carrée est définie sur[0;+∞[et est dérivable sur]0;+∞[. Selon le théorème, cette fonction est continue sur]0;+∞[. Mais, sa limite en 0 est 0 donc elle est continue sur[0;+∞[. 9Fiches de Mathématiques2 LES FONCTIONS
Nombre dérivé
lim h→0f(a+h)-f(a)h=? f(a+h)=f(a)+?h+h?(h)avec lim h→0?(h)=0Si ces propositions sont vraies,fest dérivable enaet?est le nombre dérivé defenanotéf?(a).
Sifest dérivable ena, la courbe?fadmet au pointA(a;f(a))une tangente?dont le coefficient directeur estf?(a). L"équation de?est : y=f?(a)×(x-a)+f(a)Si la limite du taux d"accroissement entreaeta+hdefest±∞, alorsfn"est pas dérivable. Il y a pas
de tangente verticale ena.Si les limites sont différentes à droite et à gauche, alorsfn"est pas dérivable ena. Il y a un point
anguleux ena.Théorème des valeurs intermédiaires
Sifest continue sur[a;b], alors, pour tout réelkcompris entref(a)etf(b), il existe au moins un réelcappartenant à[a;b]tel que f(c) =k. L"équationf(x)=kadmet au moins une solution dans[a;b]. Théorème de bijection ou corollaire du theorème des valeursintermédiaires Sifest continue et strictement croissante sur[a;b],f([a;b]) =[f(a);f(b)].Alors,
?y?[f(a);f(b)], il existe un et un seul réelc?[a;b]tel quef(c) =y. L"équationf(x)=yadmet une et une seule solution dans[a;b]. Idem pour une fonction strictement décroissante.f([a;b]) =[f(b);f(a)].Toute fonction continue et strictement monotone sur un intervalle donné réalise une bijection...
Démonstration (ROC)
?Supposonsfcontinue et strictement croissante sur[a;b]. ?Existence :fest continue sur[a;b]. D"après le théorème des valeurs intermédiaires,?y?[f(a);f(b)], l"équation
f(x)=yadmet au moins une solution. ?Unicité :Supposons quef(c1) =f(c2) =yavecc1 On dit quef, fonction dérivable sur un intervalleI, est solution de l"équation différentielley?=k.y, Il existeune et une seule fonctiondérivable sur?telle quey?=yety(0)=1 (condition initiale). C"est laCela contredit la suppositionf(c1)=f(c2)=y.
Donc, il existe un seul réelctel quef(c) =y.
10 Fiches de Mathématiques3 FONCTION EXPONENTIELLE ET ÉQUATION DIFFÉRENTIELLE 2.5 Dérivation
Rappels
?fest constante si et seulement sif?est nulle. ?fest croissante si et seulement sif?est positive. ?fest décroissante si et seulement sif?est négative. ?Sif(a)est un extremum local defenaalors,f?(a) =0. (réciproque fausse) ?Sif?s"annule et change de signe enaalors,f(a)est un extremum local. Dérivée d"une fonction composée
gdérivable surJetudérivable surItels que :?x?I,u(x)?J. Alors,f=g◦uest dérivable surIet on a(g◦u)?(x)=g?(u(x))×u?(x) (g◦u)?= (g?◦u)×u? Exemples importants
u, fonction positive et dérivable surI. ?f=? uest dérivable et donne :(?u)?=u?2?u. ?f=unest dérivable et donne :(un)?=n×un-1×u? 3 Fonction exponentielle et équation différentielle
Définition
Fonction exponentielle
Equationy?=a.y
L"ensemble des solutions dans?de l"équationy?=ayest l"ensemble des fonctions x?→c.eax oùcest un réel quelconque. Il existeune unique solutionvérifiant la condition initialey?(x0) =y0. Equationy?=ay+b
Les solutions de l"équation(E):y?=a.y+bsont les fonctions définies sur?, de la formef-baoùf est solution dey?=ay. C"est-à-dire x?→Ceax-b a oùC??. Siy(x0) =y0,(E)admetune uniquesolution. 4 Fonction logarithme népérien
Propriétés
?ln(1) =0?ln(e)=1 ?eln(a)=a?ln(ea) =a ?ln(a×b)=ln(a)+ln(b)?lna b=ln(a)-ln(b) ?ln1 a=-ln(a)?ln?a=12ln(a) ?ln(an)=n×ln(a) Etude de la fonction
?La fonction ln est définie et continue sur]0;+∞[. ? ?x?]0;+∞[, ln?(x)=1 x. ?La fonction ln est croissante sur]0;+∞[. ?limx→+∞ln(x)=+∞et limx→0ln(x)=-∞ ?limx→+∞ln(x) x=0 et limx→0x.ln(x)=0 ?limx→1ln(x) x-1=1 et limx→0ln(x+1)x=1 12 Fiches de Mathématiques5 FONCTIONS PUISSANCES ET CROISSANCES COMPARÉES Démonstration (ROC)
Soita>0, démontrons que lim
h→0ln(a+h)-ln(a)h=1aou limx→0ln(a)-ln(x)a-x=1a. PosonsA=ln(a),a=eAetX=ln(x),x=eX.
ln(a)-ln(x) a-x=A-XeA-eX=1eA-eX A-X. Comme ln est continue sur]0;+∞[, limx→aln(x)=ln(a). lim X→ln(a)e
A-eX A-X=limX→Ae
A-eXA-X=exp?(A) =exp(A) =exp(ln(a)) =a.
lim x→aln(a)-ln(x) a-x=limX→A1eA-eX A-X=1a.
D"où ln est dérivable ena>0 et ln?(a)=1
a. Fonctionln◦u
(ln◦u)?(x) =u?(x)u(x)quotesdbs_dbs41.pdfusesText_41
[PDF] formule complexe math
[PDF] formules nombres complexes terminale s
[PDF] formule complexe exponentielle
[PDF] formule complexe module
[PDF] liaison intermoléculaire et intramoléculaire
[PDF] interaction de van der waals liaison hydrogène
[PDF] interaction intermoléculaire 1ere s
[PDF] force de debye
[PDF] nombres complexes terminale s annales
[PDF] liaison intermoléculaire définition
[PDF] force dipole dipole
[PDF] interaction intermoléculaire definition
[PDF] force de debye exemple
[PDF] formule du champ magnétique
