 Système de coordonnées
Système de coordonnées
Un jeu de coordonnées cylindriques est donc : Un autre : ▫ Comme des volumes limités par des portions de sphères ou de cônes. Les coordonnées sphériques ...
 COORDONNÉES CARTÉSIENNES CYLINDRIQUES
COORDONNÉES CARTÉSIENNES CYLINDRIQUES
http://mawy33.free.fr/cours%20sup/35-500%20coords.pdf
 Syst`emes de coordonnées
Syst`emes de coordonnées
En coordonnées cylindriques un point M de l'espace est repéré comme un point En coordonnées sphériques
 lestransformations du système de coordonnées - effets sur les
lestransformations du système de coordonnées - effets sur les
une symétrie sphérique et même cylindrique
 Expressions du gradient _cartésien cylindrique
Expressions du gradient _cartésien cylindrique
http://ts2-thierrymaulnier.wifeo.com/documents/Expressions-du-gradient-_cartsien-cylindrique-sphrique.pdf
 Les systèmes de coordonnées.
Les systèmes de coordonnées.
4 sept. 2023 ... coordonnées qui figurent explicitement à votre programme : cartésiennes cylindriques
 UCBL – L1 PCSI – UE Math 2 Fonctions de plusieures variables et
UCBL – L1 PCSI – UE Math 2 Fonctions de plusieures variables et
les coordonnées cylindriques et sphériques: A “ p´1 1
 Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes cylindriques
 DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
COORDONNÉES CYLINDRIQUES ET SPHÉRIQUES. I. DÉRIVATION VECTORIELLE. I On peut passer facilement des coordonnées cylindriques aux coordonnées cartésiennes :.
 COORDONNÉES CARTÉSIENNES CYLINDRIQUES
COORDONNÉES CARTÉSIENNES CYLINDRIQUES
http://mawy33.free.fr/cours%20sup/35-500%20coords.pdf
 Système de coordonnées
Système de coordonnées
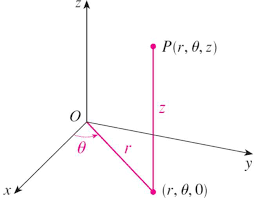
Dans le système de coordonnées cylindriques un point P de l'espace (3-D) est représenté Le système de coordonnées sphériques est un autre système de.
 Chapter 1 - Syst`emes de coordonnées
Chapter 1 - Syst`emes de coordonnées
1.1.1 Repérage d'un vecteur en coordonnées cylindriques En coordonnées sphériques un point M(r) est considéré comme un point d'une sph`ere centrée sur.
 MATHS.5:SYSTEMES DE COORDONNEES A) Coordonnées
MATHS.5:SYSTEMES DE COORDONNEES A) Coordonnées
I) COORDONNEES POLAIRES ET CYLINDRIQUES Vecteurs de la base (base mobile cylindrique) :( ... Coordonnées sphériques : r et ?
 DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
Dérivation vectorielle – Bases de projection (33-103). Page 1 sur 5. JN Beury. DÉRIVATION VECTORIELLE. COORDONNÉES CYLINDRIQUES ET SPHÉRIQUES.
 Transformation coordonnées
Transformation coordonnées
une symétrie sphérique et même cylindrique
 Les différents systèmes de coordonnées
Les différents systèmes de coordonnées
Attention les angles ? des coordonnées cylindriques et sphériques sont différents. 1. Page 2. Quelques surfaces élémentaires. • Surface élémentaire d'un
 Expressions du gradient _cartésien cylindrique
Expressions du gradient _cartésien cylindrique
http://ts2-thierrymaulnier.wifeo.com/documents/Expressions-du-gradient-_cartsien-cylindrique-sphrique.pdf
 TD no 1. Outils mathématiques
TD no 1. Outils mathématiques
Exercice I. Coordonnées cartésiennes cylindriques
 Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes cylindriques

Année universitaire 2016/2017.
U.E. 2P021
TD n o1. Outils mathématiques Exercice I. Coordonnées cartésiennes, cylindriques, sphériques Définir dans le système de coordonnées le plus approprié les surfaces suivantes1. Le plan P infini (xOy):En coordonnées cartésiennes le plan P est défini par:
z=0 En coordonnées cylindriques le plan P est défini par: z=0 En coordonnées sphériques le plan P est défini par: ==2Les 3 systèmes de coordonnées semblent à priori appropriés.2. Le disque D de centre O et de rayon R, inclus dans le plan (xOy)
En coordonnées cartésiennes le disque D est défini par: z=0;qx 2+y2R En coordonnées cylindriques le disque D est défini par: z=0;R En coordonnées sphériques le disque D est défini par: ==2;rR Les systèmes de coordonnées cylindriques et sphériques semblent à priori les plus appro- priés.3. Le tube T d"axe (Oz), de rayon R, compris entre les plans z=0 et z=H 1 En coordonnées cartésiennes le tube T est défini par:0zH;qx
2+y2=R
En coordonnées cylindriques le tube T est défini par:0zH;=R
En coordonnées sphériques le tube T est défini par:0rcos()H;rsin()=R
Le système de coordonnées cylindriques semble à priori le plus approprié.4. La sphère S et la boule B de centres O et de rayons R
En coordonnées cartésiennes la sphère S et la boule B sont définies par: qx2+y2+z2=Rpour S;qx
2+y2+z2Rpour B
En coordonnées cylindriques la sphère S et la boule B sont définies par: q2+z2=Rpour S;q
2+z2Rpour B
En coordonnées sphériques la sphère S et la boule B sont définies par: r=Rpour S;rRpour B Le système de coordonnées sphériques semble à priori le plus approprié.2 Exercice II. Intégrales surfaciques, volumiques Calculer à l"aide d"une intégrale les quantités suivantes :1. L"aire du disque DEn coordonnées cylindriques:
Pour le disque, z est constant et vaut 0. En revanche,varie de 0 à R et l"anglede 0 à2. On a donc:
A D=Z R 0Z 2 0 dzdd=2Z R 0 d=2h1=22iR0=R22. La surface et le volume du tube T
En coordonnées cylindrique:
Si le tube est fermé, alors il y a trois surfaces à considérer: les couvercles supérieur et
inférieur ainsi que la surface latérale. On a donc: A T=Z 2 0Z h 0Rddz=2Rh(1)
V T=Z R 0Z h 0Z 2 0 ddzd=2hZ R 0 d=hR2(2)3. L"aire de la sphère SEn coordonnées sphériques:
A s=Z 0Z 2 0RdRsin()d=2Z
0R2sin()d=4R24. Le volume de la boule B
En coordonnées sphériques:
V B=Z R 0Z 0Z 2 0 ddsin()d=2Z R 0Z 02dsin()d=4=3R33
Calculer la charge totale portée par :
1. Le disque D de densité surfacique de charge(;)=0sin(=2)La charge totale est égale à la charge de l"ensemble du disque. On intègre donc la densité
surfacique de charge sur l"ensemble de la surface du disque: Q D=0Z R 0Z 2 0 dsin(=2)d=(R2=2)0Z 2 0 sin(=2)d=R20hcos(=2)i 20=2R202. Le tube T de densité surfacique de charge(;z)=0sin(=2)La charge totale est égale à la charge de l"ensemble du tube. On intègre donc la densité
surfacique de charge sur l"ensemble de la surface du tube. Le tube étant ouvert on a: Q T=0Z H 0Z 2 0 dzsin(=2)Rd=RH0Z 2 0 sin(=2)d=4RH03. Le cylindre C inclus dans T et de densité volumique de charge!(;;z)=!0zHRsin(=2)La charge totale est égale à la charge de l"ensemble du tube. On intègre donc la densité
volumique de charge sur l"ensemble du volume du cylindre: Q C=!0Z R 0Z H 0Z 2 0 dzddzHR sin(=2)=4!0Z R 0Z H 0z2HR =23 R2H!04. LabouleBdedensitévolumiquedecharge(r)=kr er=a,oùaetksontdesconstantes.Comment se comporte cette charge lorsqueR!+1? 4 Q B=Z R 0kr er=adrZ 0 rdZ 2 0 rsind =kZ R 0 rer=adrZ 0 sindZ 2 0 d =4kZ R 0 rer=adr on fait une intégration par partie: on pose : u=r v=aer=a u0=1v0=er=a
d 0ou : QB=4khraer=aiR
0+4kaZ
R 0 er=adr =4kRaeR=a+4kha2er=aiR 0 =4kRaeR=a4ka2eR=a+4ka2 =4ka21eR=a(1+Ra
QuandR!+1on aeR=a(1+Ra
)!0 et doncQB!4ka2. Tout se passe comme si onavait une sphère de rayon a et de densité surfacique de charge(r;;)=k.Exercice III. Gradient d"un champ scalaire et circulation d"un champ vec-
torielCalculer le gradient du champ scalaire:f(r;;)=cos=r2Compte tenu de la forme du champ scalaire, on utilise l"expression du gradient en
coordonnées sphériques fournie dans le formulaire. On a donc rf=@rf~er+1r @f~e+1rsin@f~e=1r32cos~ersin~e
avec les notations@r=@@r,@=@@ et@=@@ .Soit ~E(x;y;z)un champ vectoriel tel queEx=2(ax+by3),Ey=2(ay+3bxy2)etEz=0(a;b;c constantes)1. Calculer le potentiel V dont dérive le champ
~E. 5On a par définition
~E=~rV. S"il on adopte le système de coordonnées cartésiennes, on en déduit tout simplement que xV=2(ax+by3))V=ax22by3x+k1(y;z) En dérivant notre nouvelle expression de V on obtient: yV=2(12 @yk1(y;z)+3bxy2) En comparant avec l"expression deEyon a:@yk1(y;z)=2ay. Par conséquent,V=a(x2+b2)2by3x+k2(z)
Comme@zV=Ez=0 on obtient finalement:
V(x;y;z)=a(x2+y2)2by3x+cste2. Calculer la circulationC1de~Eentre les points (x=0;y=0) et (x=1;y=0). Vérifier qu"on a
bienC1=V(0;0)V(1;0).Le champ ~Edérive d"un potentiel donc sa circulation ne dépend pas du chemin suivi. On choisit alors le chemin le plus simple, selon l"axeOx,~l(t)=t~ex(ce qui équivaut àx(t)=t ety(t)=0), pourt2[0;1]. C 1=Z t=1 t=0~E(x(t);y(t))d~l(t)=Z t=1 t=0~E(t;0)dt~ex=Z x=1 x=0E x(t;0)dx=Z x=1 x=02axdx=a=V(0;0)V(1;0)3. Calculer la circulationC2du champ vectoriel~B(;;z)=k(r)~esur le cercle de centreO, de
rayonRet d"axeOz, et oùkest une fonction quelconque der.Le chemin le long du cercle est paramétré, pourt2[0;2], comme~l(t)=R~e(t), où de
manière équivalente comme(t)=Ret(t)=t. On trouve ensuited~l(t) en utilisant la dérivée de ~e:d~l(t)=Rd~e=Rd~edt dt=Rddt ~edt=R~edtFinalement,
C2=Rt=2
t=0~B((t)=R;(t);z=0)d~l(t)=R20k(R)Rdt=2Rk(R)6
Exercice IV. Divergence et rotationnel d"un champ vectoriel Dessiner l"allure des champs vectoriels suivant et calculer leur divergence et leur rotationnel. 1. ~A1(x;y;z)=a1x~exdiv ~A1=a1 !rot~A1=~02. ~A2(x;y;z)=a2y~exdiv ~A2=0 !rot~A2=a2~ez3. ~A3(;;z)=a3~e 7 En utilisant cette fois l"expression de la divergence en coordonnées cylindriques on a: div ~A3=2a3 !rot~A3=~0-6-4-20246 6 4 2 0 2 4 64.~A4(r;;)=a4r
2er=r0~er+sin~ediv
~A4=a4r0r2er=r0
rot~A4=a4r32cos~er+sin~e
8Exercice V. Développements limités
On rappelle la formule de Taylor à l"ordre n :
f(a+x)=n X k=0x kk!f(k)(a)=f(a)+x1! f(1)(a)+x22! f(2)(a)+x33! f(3)(a)+:::xnn!f(n)(a)Calculer les développements limités au voisinage de zéro à l"ordre 4 des fonctions suivantes :
1.f(x)=cosxf(x)=1x2=2+x4=24+o(x4)2.g(x)=sinxg(x)=xx3=6+o(x4)3.h(x)=expxh(x)=1+x+x2=2+x3=6+x4=24+o(x4)4.i(x)=(1+x)ni(x)=1+nx+n(n1)x2=2+n(n1)(n2)x3=6+n(n1)(n2)(n3)x4=24+o(x4)Rappel:A(x)=x!0o(xn) si et seulement siA(x)x
n!x!00, etB(x)=x!0O(xn) si et seulement si limx!0B(x)x n<1. 9quotesdbs_dbs28.pdfusesText_34[PDF] comprendre la cop21 et ses enjeux - Toute l 'Europe
[PDF] La COP22, La COP de l 'Action
[PDF] Información sobre las copias de seguridad - UPF
[PDF] Qu 'est ce que Copie En Ligne ?
[PDF] 02 - Liste docs Mge et VO div - Les Consulats Généraux de France
[PDF] Demande TR AN majeur Sénégal - Ambassade de France au Sénégal
[PDF] CONCOURS COMPLEMENTAIRES 2013 1er GRADE - Enm
[PDF] Aide-mémoire TI-Nspire CAS - Mathématiques du Cnam
[PDF] Circular 1 Copyright Basics - Copyright Office
[PDF] Un logiciel libre de détection du plagiat - RMLL
[PDF] Chirurgie de la cataracte - CSSS de Chicoutimi
[PDF] The Holy Quran Arabic text with French translation - Al Islam
[PDF] Le Coran mecquois - Sami Aldeeb
[PDF] le saint coran en phonetique - Fichier-PDFfr
