 Système de coordonnées
Système de coordonnées
Un jeu de coordonnées cylindriques est donc : Un autre : ▫ Comme des volumes limités par des portions de sphères ou de cônes. Les coordonnées sphériques ...
 COORDONNÉES CARTÉSIENNES CYLINDRIQUES
COORDONNÉES CARTÉSIENNES CYLINDRIQUES
http://mawy33.free.fr/cours%20sup/35-500%20coords.pdf
 Syst`emes de coordonnées
Syst`emes de coordonnées
En coordonnées cylindriques un point M de l'espace est repéré comme un point En coordonnées sphériques
 lestransformations du système de coordonnées - effets sur les
lestransformations du système de coordonnées - effets sur les
une symétrie sphérique et même cylindrique
 Expressions du gradient _cartésien cylindrique
Expressions du gradient _cartésien cylindrique
http://ts2-thierrymaulnier.wifeo.com/documents/Expressions-du-gradient-_cartsien-cylindrique-sphrique.pdf
 Les systèmes de coordonnées.
Les systèmes de coordonnées.
4 sept. 2023 ... coordonnées qui figurent explicitement à votre programme : cartésiennes cylindriques
 UCBL – L1 PCSI – UE Math 2 Fonctions de plusieures variables et
UCBL – L1 PCSI – UE Math 2 Fonctions de plusieures variables et
les coordonnées cylindriques et sphériques: A “ p´1 1
 TD no 1. Outils mathématiques
TD no 1. Outils mathématiques
Année universitaire 2016/2017. U.E. 2P021. TD no 1. Outils mathématiques. Exercice I. Coordonnées cartésiennes cylindriques
 Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes cylindriques
 DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
COORDONNÉES CYLINDRIQUES ET SPHÉRIQUES. I. DÉRIVATION VECTORIELLE. I On peut passer facilement des coordonnées cylindriques aux coordonnées cartésiennes :.
 COORDONNÉES CARTÉSIENNES CYLINDRIQUES
COORDONNÉES CARTÉSIENNES CYLINDRIQUES
http://mawy33.free.fr/cours%20sup/35-500%20coords.pdf
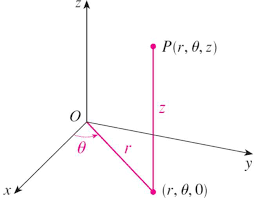
 Système de coordonnées
Système de coordonnées
Dans le système de coordonnées cylindriques un point P de l'espace (3-D) est représenté Le système de coordonnées sphériques est un autre système de.
 Chapter 1 - Syst`emes de coordonnées
Chapter 1 - Syst`emes de coordonnées
1.1.1 Repérage d'un vecteur en coordonnées cylindriques En coordonnées sphériques un point M(r) est considéré comme un point d'une sph`ere centrée sur.
 MATHS.5:SYSTEMES DE COORDONNEES A) Coordonnées
MATHS.5:SYSTEMES DE COORDONNEES A) Coordonnées
I) COORDONNEES POLAIRES ET CYLINDRIQUES Vecteurs de la base (base mobile cylindrique) :( ... Coordonnées sphériques : r et ?
 DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
DÉRIVATION VECTORIELLE COORDONNÉES CYLINDRIQUES ET
Dérivation vectorielle – Bases de projection (33-103). Page 1 sur 5. JN Beury. DÉRIVATION VECTORIELLE. COORDONNÉES CYLINDRIQUES ET SPHÉRIQUES.
 Transformation coordonnées
Transformation coordonnées
une symétrie sphérique et même cylindrique
 Les différents systèmes de coordonnées
Les différents systèmes de coordonnées
Attention les angles ? des coordonnées cylindriques et sphériques sont différents. 1. Page 2. Quelques surfaces élémentaires. • Surface élémentaire d'un
 Expressions du gradient _cartésien cylindrique
Expressions du gradient _cartésien cylindrique
http://ts2-thierrymaulnier.wifeo.com/documents/Expressions-du-gradient-_cartsien-cylindrique-sphrique.pdf
 TD no 1. Outils mathématiques
TD no 1. Outils mathématiques
Exercice I. Coordonnées cartésiennes cylindriques
 Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes
Expressions des opérateurs en coordonnées cartésiennes cylindriques
Chapter 1
Syst`emes de coordonn´ees
1.1 Rep`ere cart´esien
Un rep`ere cart´esien est d´efini par un point origineOet trois axes (Ox,Oy,Oz) perpendiculaires
entre eux. Les vecteurs unitaires port´es par les axes sont: ?ex,?ey,?ez. (voir figure 1.1a)) M"O z x y Mez ey ex r M"O z M ez eyex A( )M a)b) y xFigure 1.1:
On doit bien noter la disposition relative des directions (Ox,Oy,Oz). Telles qu"elles sontplac´ees, elles d´efinissent un tri`edre direct. Dans un teltri`edre, un bonhomme transperc´e des pieds
`a la tˆete parOy, regardant la directionOz, a la directionOx`a sa gauche. On peut noter aussi que
Ox,Oy,etOzsont respectivement orient´es selon les directions du pouce, de l"index et du majeurde la main droite. Un pointMde l"espace est rep´er´e par les trois composantes du vecteur-→r
joignantO`aM(-→r=--→OM) (voir fig. 1.1a) : r(x,y,z) =x?ex+y?ey+z?ez M ?est la projection deMdans le plan (x0y). Les composantesxetyde-→rsont les coordonn´ees du pointM?dans ce plan. La composantezest obtenue en tra¸cant la parall`ele `aOM?passant par M. On dira indistinctement qu"un objet se trouve au pointMou en-→r.1.1.1 Rep´erage d"un vecteur en coordonn´ees cylindriques
Quand il s"agit de rep´ererun vecteur
-→A(M) dont le point d"application est situ´e au pointM(x,y,z),ou-→r(x,y,z), on peut d´ecrire ce vecteur avec le mˆeme base de vecteurs unitaires?ex,?ey,?ez(voir
fig.1.1b)). Nous appelons donc ?ex,?ey,?ez, un r´ep`ere orthonorm´eglobalparce qu"on peut l"utiliser `a d´ecrire un vecteur ayant n"importe lequel point d"application.1.2. COORDONN´EES CYLINDRIQUES2
1.2 Coordonn´ees cylindriques
1.2.1 Rep´erage d"un point en coordonn´ees cylindriques
En coordonn´ees cylindriques, un pointMde l"espace est rep´er´e comme un point de cylindre (droit,
`a base circulaire) dont l"axeOzest g´en´eralement confondu avec l"axeOzdu rep`ere cart´esien.
Le pointM(ou-→r) est rep´er´e par
•le rayonρdu cylindre sur lequel il s"appuie •zsa cote par rapport au plan de r´ef´erencexOy •φl"angle (Ox,OM?) o`uM?est la projection deMsur le planxOy.La notation
-→r(ρ,φ,z) vient se substituer `a-→r(x,y,z) du rep`ere cart´esien. Vous pouvez facile-
ment v´erifier que, pour un point donn´e, les composantes cart´esiennes et cylindriques sont li´ees par
x=ρcosφ y=ρsinφ z=z M" ?O z x y M e? ez e?Figure 1.2:
1.2.2 Rep´erage d"un vecteur en coordonn´ees cylindriques
Nous nous posons la question de rep´erer un vecteur dont le point d"application est situ´e au point
M(ρ,φ,z), ou-→r(ρ,φ,z). Pour cela nous attachons `aMun rep`ere orthonorm´e local (?eρ,?eφ,?ez).
Nous l"appelonslocalparce qu"il n"est pas le mˆeme pour tous les pointsMde l"espace. Ce rep`ere local est fait de 3 vecteurs unitaires de base orthogonaux ( ?eρ,?eφ,?ez) : ?eρ(ou?uρou?ρ) est un vecteur parall`ele `a---→OM?. ?eφ(ou?uφou?φ) est parall`ele au vecteur tangent enM?au cercle de rayonOM?contenu dans le planxOy ?ez(ou?uzou?z) est parall`ele `a l"axeOz Dans ce rep`ere, le vecteur champ ´electrique a 3 composantes et s"´ecrit E(M) =Eρ?eρ+Eφ?eφ+Ez?ezou-→E(M) =(( E E E z))1.2. COORDONN´EES CYLINDRIQUES3
Au pointM, la relation entre les vecteurs unitaires (?eρ,?eφ,?ez) et les vecteurs unitaires cart´esiennes
?ex,?ey,?ez) s"´ecrivent : eρ= cosφ?ex+ sinφ?ey eφ=-sinφ?ex+ cosφ?ey ez=?ez(1.1) On peut voir cette relation comme une relation matricielle (tensorielle) (?eρ eφ ez)) cosφsinφ0 -sinφcosφ00 0 1))
(?ex ey ez)) =T((?ex ey ez)) Les relation inverses sont obtenues en prenant l"inverse dela matriceT. Puisque les deux bases sont orthonorm´ees, on aT-1=Tto`uTtest la transpose de la matriceT. On obtient de cette mani`ere les vecteurs unitaires ( ?ex,?ey,?ez) en fonction des (?eρ,?eφ,?ez) : (?ex ey ez)) cosφ-sinφ0 sinφcosφ00 0 1))
(?eρ eφ ez)) c"est-`a-dire. ex= cosφ?eρ-sinφ?eφ ey= sinφ?eρ+ cosφ?eφ ez=?ez On peut ´egalement v´erifier ces relations avec de la g´eom´etrie.1.2.3 Position et d´eplacement (diff´erentielle) en coordonn´ees cylindriques
On se rappelle qu"en coordonn´ees cart´esiennes, le vecteur position s"´ecritOM=x?ex+y?ey+z?ez
et la diff´erentielle de cette position s"´ecrit dOM≡∂--→OM
En coordonn´ees cylindriques par contre, on ´ecritOM=ρ?eρ+z?ez
et la diff´erentielle s"exprime : dOM=∂--→OM
Si l"on veut exprimerd--→OMen coordonn´ees cylindriques, il faut tenir compte du fait que le vecteur
unitaire local ?eρd´epend de la coordonn´eeφ(voir eq.(1.1)) : OM OM∂φ=ρ∂?eρ∂φ=ρ∂∂φ(cosφ?ex+ sinφ?ey) =ρ(-sinφ?ex+ cosφ?ey) =ρ?eφ
Un d´eplacement en coordonn´ees cylindriques s"exprime donc1.3. COORDONN´EES SPH´ERIQUES4
Cette formule est tr`es utile afin d"en d´eduire des volumes et des surfaces ´el´ementaires. Par exemple,
un ´el´ement de volume ´el´ementaire en coordonn´ees cylindriques s"exprime dV= (dρ)(ρdφ)(dz) =ρdρdφdz(1.3) Exemple :On peut utiliser ce r´esultat `a d´eriver la formule pour un cylindre de rayonRet de coteL:Volume
cylindreR,L=??? cylindre dV=? R 0 dρ? 2π 0ρdφ?
L 0 dz=L? R 0ρdρ?
2π 0 dφ = 2πL? R 0ρdρ=πR2L
1.2.4 Gradient en coordonn´ees cylindriques
La diff´erentielle en coordonn´ees cylindriques d"un champscalaire Φ s"exprime : dΦ =∂Φ Le gradient en coordonn´ees cylindriques est d´efinie telleque : dΦ =---→gradΦ·d--→OM(1.5) Une comparaison entre (1.2), (1.4) et (1.5) montre que l"expression du gradient en coordonn´ees cylindriques s"´ecrit : gradΦ =∂Φ Exemple : Lorsque le potentiel ´electriqueV(M) est exprim´e en coordonn´ees cylindriques(ρ,θ,z), les composantes du champ ´electrique dans le rep`ere cylindrique attach´e au pointMsont
donn´ees par:-→E(ρ,φ,z) =----→gradV(ρ,φ,z)E=Eρ?eρ+Eφ?eφ+Ez?ezE
ρ=-∂V
Eφ=-1
ρ∂V∂ρ
E z=-∂V ∂zLe potentiel cr´e´e par une distribution lin´eique de charge avec une densit´e par unit´e de longueur
λest donn´e parV(ρ) =-λ
2π?0ln(ρ) +Cte. On obtient imm´ediatement le champ ´electrique par
E(ρ) =----→gradV(ρ) =λ
2π?0ρ?eρ
1.3 Coordonn´ees sph´eriques
1.3.1 Rep´erage d"un point en coordonn´ees sph´eriques
En coordonn´ees sph´eriques, un pointM(r) est consid´er´e comme un point d"une sph`ere centr´ee sur
O. Le pointMest rep´er´e
•par le rayonrde la sph`ere `a laquelle il appartient •L"angleθentre la direction-→Ozet la direction--→OM.θ= (-→Oz,--→OM)•l"angleφentre la direction-→Oxet la direction---→OM?o`uM?est la projection deMdans le
planxOy.:φ= (-→Ox,---→OM?)1.3. COORDONN´EES SPH´ERIQUES5
M" ?O z x y r M e ere? M""Figure 1.3:Coordonn´ees sph´eriques
Un pointM(r) ´etant donn´e, on trouve que ses coordonn´ees cart´esiennes s"´ecrivent en fonction
des coordonn´ees sph´eriques; ainsi: x=rsinθcosφ y=rsinθsinφ z=rcosθEn g´eographie, o`u on est amen´e `a rep´erer un point sur la sph`ere terrestre, l"angleθindiquerait
la latitude par rapport au pˆole nord et l"angleφ, la longitude est par rapport au m´eridien de
r´ef´erence.1.3.2 Rep´erage d"un vecteur en coordonn´ees sph´eriques
En coordonn´ees sph´eriques, un vecteur-→E(M) (ou simplement-→E(-→r)) attach´e au pointM(r) est
rep´er´e par trois composantes (Er,Eθ,Eφ) dans un rep`ere orthonorm´elocal(?er,?eθ,?eφ) :
E(M) =Er?er+Eθ?eθ+Eφ?eφ
avec ?er(ou?urou?r) est un vecteur parall`ele `a--→OM. ?eθ(ou?uθou?θ) est parall`ele au vecteur tangent enMau cercle de rayonrd´ecrit dans le plan qui contient `a la fois les directions-→Oz,--→OMetOM?. ?eφ(ou?uφou?φ) est tangent enMau cercle de centreM??et de rayonM??M=OM?, contenu dans le plan perpendiculaire `a-→Oz. Au pointM, la relation entre les vecteurs unitaires (?er,?eθ,?eφ) et les vecteurs unitaires cart´esiennes ( ?ex,?ey,?ez) s"´ecrivent : er= sinθcosφ?ex+ sinθsinφ?ey+ cosθ?ez eθ= cosθcosφ?ex+ cosθsinφ?ey-sinθ?ez eφ=-sinφ?ex+ cosφ?ey(1.7) On peut voir cette relation comme une relation matricielle (tensorielle) (?er eθ eφ)) sinθcosφsinθsinφcosθ cosθcosφcosθsinφ-sinθ -sinφcosφ0)) (?ex ey ez)) =T((?ex ey ez))1.3. COORDONN´EES SPH´ERIQUES6
ainsi que les relation inverses (?ex ey ez)) =T-1((?er eθ eφ)) =Tt((?er eθ eφ)) sinθcosφcosθcosφ-sinφ sinθsinφcosθsinφcosφ cosθ-sinθ0)) (?er eθ eφ)) o`u nous avons encore utilis´e le fait que les deux bases sontorthonom´es donne implique T -1=Tt. Exemple de coordonn´ees sph´eriques :Consid´erons le potentiel et le champ ´electriquescr´e´espar une charge ponctuelleqplac´ee `a l"origineO. En coordonn´eessph´eriques, ceux-ci s"expriment
enti`erement en fonction du vecteur radial-→ret du coordonn´ee radialr=??-→r??:V(r) =q
4π?01r-→E(-→r) =q4π?0?
err2=q4π?0-→ rr3 ce qui est plus simple et "naturel" que les expressions en coordonn´ees cart´esiennes :V(x,y,z) =q
4π?01?x2+y2+z2-→E(x,y,z) =q4π?0x
?ex+y?ey+z?ez(x2+y2+z2)3/21.3.3 Position et d´eplacement (diff´erentielle) en coordonn´ees sph´eriques
En coordonn´ees sph´eriques, le vecteur position s"´ecritsimplementOM=r?er
La diff´erentielle,d--→OM, en coordonn´ees sph´eriques s"´exprime: dOM=∂--→OM
Afin d"exprimerd--→OMen coordonn´eessph´eriques, il faut tenir compte du fait que le vecteur unitaire
local ?erd´epend des coordonn´eesθ, etφ(mais pas surr) : OM ∂r=?er+r∂?er∂r=?er OM ∂θ=r∂?er∂θ=r?eθ OM Un d´eplacement en coordonn´ees sph´eriques s"exprime doncCette formule est tr`es utile afin d"en d´eduire des volumes et des surfaces ´el´ementaires. Par exemple,
un ´el´ement de volume ´el´ementaire en coordonn´ees cylindriques est dV= (dr)(rdθ)(rsinθdφ) =r2drsinθdθdφ(1.9) Exemple :On peut utliser ce r´esultat `a d´eriver la formule pour le volume d"une sph`ere de rayonR:Volume
sph`ere de rayonR=??? sph`ere dV=? R 0 dr? 0 dθ? 2π 0 r2sinθdφ=? R 0 r2dr? 0 sinθdθ? 2π 0 dφ = 2π? R 0 r2dr? 1 -1d(cosθ) = 4π? R 0 r2dr=4π 3R31.3. COORDONN´EES SPH´ERIQUES7
1.3.4 Gradient en coordonn´ees sph´eriques
La diff´erentielle en coordonn´ees sph´eriques s"´ecrit : dΦ =∂ΦUne comparaison entre cette ´equation et l"´eq.(1.8) montre que l"expression du gradient en coor-
donn´ees sph´eriques est donn´ee par : gradΦ =?er∂Φ Exemple :Pour une charge ponctuelle situ´ee `a l"origine par exemple, si on se rappelle queson potentiel ´electrique, s"´ecritV(r) =q/(4π?0r), on obtient toute suite son champ ´electrique en
coordonn´ees sph´eriques :E(-→r) =----→gradV(r) =-?er∂V
∂r=-q4π?0?er∂∂r1r q4π?0?
err2 alors que le calcul est plus on´ereux en coordonn´ees cart´esiennesE(x,y,z) =----→gradV(x,y,z) =-q
4π?0?
q4π?0?
q4π?0x
?ex+y?ey+z?ez(x2+y2+z2)3/2quotesdbs_dbs23.pdfusesText_29[PDF] comprendre la cop21 et ses enjeux - Toute l 'Europe
[PDF] La COP22, La COP de l 'Action
[PDF] Información sobre las copias de seguridad - UPF
[PDF] Qu 'est ce que Copie En Ligne ?
[PDF] 02 - Liste docs Mge et VO div - Les Consulats Généraux de France
[PDF] Demande TR AN majeur Sénégal - Ambassade de France au Sénégal
[PDF] CONCOURS COMPLEMENTAIRES 2013 1er GRADE - Enm
[PDF] Aide-mémoire TI-Nspire CAS - Mathématiques du Cnam
[PDF] Circular 1 Copyright Basics - Copyright Office
[PDF] Un logiciel libre de détection du plagiat - RMLL
[PDF] Chirurgie de la cataracte - CSSS de Chicoutimi
[PDF] The Holy Quran Arabic text with French translation - Al Islam
[PDF] Le Coran mecquois - Sami Aldeeb
[PDF] le saint coran en phonetique - Fichier-PDFfr
