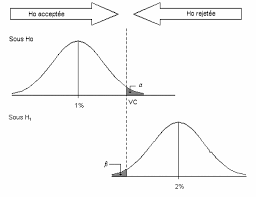
 Exercices corrigés de statistiques inférentielles – Tests dhypothèses
Exercices corrigés de statistiques inférentielles – Tests dhypothèses
Dans un centre de renseignements téléphoniques une étude statistique a montré que l'attente (en secondes) avant que la communication soit amorcée suit une loi
 MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
Si le paramètre de la loi de Student est grand la loi normale peut être utilisée pour Exercices. 1. ⋆Trouver z0.5
 L2 - Psychologie 2019-2020 - Trois exercices sur les tests
L2 - Psychologie 2019-2020 - Trois exercices sur les tests
Corrigé de l'Exercice 1. Lors d'une enquête menée en 2014 sur 450 français Puisque la table de la loi de Student ne donne que des valeurs positives
 Exercices et problèmes de statistique et probabilités
Exercices et problèmes de statistique et probabilités
Corrigés des exercices . Dans cet exercice on s'intéresse à la loi du couple (Yn
 Régression linéaire
Régression linéaire
Exercice 3.10 (Tests) Cet exercice est corrigé en annexe (sujet de décembre 2011). Néanmoins si n ≫ p
 Exercices 10.3 11.1
Exercices 10.3 11.1
13.6
 4-4-Tests corrigés
4-4-Tests corrigés
Sous l'hypothèse H0 la loi de T est la loi de Student à 5 degrés de liberté car le rendement est distribué normalement dans la population. Le seuil de
 Exercice 1 : a) Lecture de la table N(0 1) : X suit une loi normale de
Exercice 1 : a) Lecture de la table N(0 1) : X suit une loi normale de
table de Student `a 10 d.d.l.. ⇒ −t = −2.2281 : F(−t)=0.025 la loi de Student est symétrique. On cherche le fractile t1 tel que : P(T >t1)=0.95 ⇒ F(t1)
 Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Le test de Student suppose que les données sont issues d'une loi normale. Un histo- gramme des 18 différences nous montre une tendance `a la bimodalité mais le
 Leçon 21 Exercices corrigés
Leçon 21 Exercices corrigés
l'exercice). Exercice 4 (Loi de Student). Soient X et Y deux variables indépendantes. X de loi N(0
 Leçon 21 Exercices corrigés
Leçon 21 Exercices corrigés
est appelée loi de Student à n degrés de liberté. Montrer que cette loi a une densité et la décrire (ainsi que son histoire !). Exercice 5. Soient X1
 Feuille de TD 3 : Tests statistiques Exercice 1.
Feuille de TD 3 : Tests statistiques Exercice 1.
On donne le quantile d'ordre 095 pour la loi de Student (10): 1
 Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Le test de Student suppose que les données sont issues d'une loi normale. Un histo- gramme des 18 différences nous montre une tendance `a la bimodalité mais le
 S3 – STATISTIQUES INFERENTIELLES – TD et Exercices
S3 – STATISTIQUES INFERENTIELLES – TD et Exercices
S3 – STATISTIQUES INFERENTIELLES – TD et Exercices CORRIGES. I. LOIS DISCRETES. TD1 : Reconnaître et utiliser une loi hypergéométrique.
 Exercices et problèmes de statistique et probabilités
Exercices et problèmes de statistique et probabilités
Corrigés des exercices . centrale) Lois de probabilités fréquemment utilisées en statistique (Loi normale
 Exercices 10.3 11.1
Exercices 10.3 11.1
13.6
 Cours de Statistiques inférentielles
Cours de Statistiques inférentielles
La loi de Student converge en loi vers la loi normale centrée réduite. Ref : Statistique exercices corrigés
 Exercices corrigés de statistiques inférentielles. Exercice 1 Induction
Exercices corrigés de statistiques inférentielles. Exercice 1 Induction
La variable aléatoire X suit la loi normale N(m ; n ?. ). Or ici ? est inconnu donc il faut utiliser la table de la loi de Student. On cherche la valeur du réel
 Corrigé des exercices
Corrigé des exercices
16?/10?/2013 La loi de Student ne dépend ni de µ ni de la variance. On utilise une loi de Student à n-1 degrés de liberté car elle est équivalente à un ...
 MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
calculer des probabilités sur la loi normale. • utiliser les propriétés de la loi normale pour effectuer des calculs de probabilité. Loi binomiale.

Leçon 21 Exercices corrigés
(Une étoile * désignera une question de difficulté supérieure.) Exercice 1.Soit(X1;:::;Xn)un échantillon de variables aléatoires sur ;A;P), indépendantes de même loi exponentielleE(1 )de paramètre1 >0.Pour toutn1, poser comme dans la leçon,X
n=1n (X1++Xn). a) Rappeler la moyenne et la variance deX1. b) Démontrer que pour toutt >0, P jX nj t2t 2n: c) Calculer un intervalle de confiance au seuilse= 1depour l"estimateur de la moyenne lorsquen >1. d) Mêmes questions si les variablesX1;:::;Xnsont indépendantes de même loi uniformeU(0;a)sur[0;a], oùa >0est un paramètre inconnu à estimer. Indication. Sur la base de l"inégalité de Tchebychev b), choisirt >0tel que 2t2n=, autrement ditt=pn
. Dire quejX nj< trevient alors àX n1 + 1pn <P(X >150) =PXnp >150np)np(1p)(150np)2
(sous réserve que150np >0). Avec la valeurp= 0;75, la fractionnp(1p)(150np)2est plus petite que0;05dès quen166. Ainsi, en vendant moins de 166 billets, la compagnie ne prend qu"un risque inférieur à 5% de devoir indemniser des voyageurs en surnombre. D"après le théorème central limite, la probabilitéP(X >150) =PXnppnp(1p)>150nppnp(1p)
est " proche » dePG >150nppnp(1p)oùGsuit une loiN(0;1). Une table de loi normale indique queP(G > t)est de l"ordre de0;05sitest de l"ordre de1;645.Il faut alors résoudre
150nppnp(1p)1;645pour que la probabilité précédente soit
inférieure à0;05. Il ressort quen187(ce qui est plus souple que la restriction fournie par l"inégalité de Tchebychev, mais qui demande en revanche à préciser le mot "proche», source de tous les risques!). c) En faisant varier les paramètres précédents (dans l"approximation par le théorème central limite) :N= 150,p= 0;5,n272.
N= 300,p= 0;75,n381.
2N= 300,p= 0;5,n561.
Exercice 3(Processus de Poisson). SoitXn,n2N, une suite de variables aléatoires indépendantes de même loi exponentielleE()de paramètre >0. PoserSn=X1++Xn,n1, et par conventionS0= 0. Pour toutt >0, soitNt= supfn0;Sn< tg. a) Quelle est la loi deSn? b) Établir que, pour toutn2N,P(Nt=n) =P(Sn< t)P(Sn+1< t):
En déduire la loi deNt.
Indication.a) Comme somme de variables aléatoires indépendantes de même loi exponentielleE(), la loi deSnest une loi Gamma (n;)(Leçon 13). b) Observer quefSn+1< tg fSn< tgce qui conduit à l"égalité demandée. Ensuite, exprimer la probabilitéP(Sn+1< t)à partir de la densité de la loi deSn+1et effectuer une intégration par parties pour se ramener à celle deSn. Il faut trouver queNtsuit une loi de Poisson (ainsi que l"indique le titre de l"exercice). Exercice 4(Loi de Student). SoientXetYdeux variables indépendantes,Xde loiN(0;1)etYde loi Gamma
(n2 ;12 )de paramètresn2 et12 , aussi appelée loi du2àn1degrés de liberté. La loi de T n=Xq Y n est appelée loi de Student àndegrés de liberté. Montrer que cette loi a une densité, et la décrire (ainsi que son histoire!). Exercice 5.SoientX1;:::;Xndes variables aléatoires indépendantes de même loi normale centrée réduiteN(0;1)et soitXle vecteur(X1;:::;Xn). 3 SoitOune matricennorthogonale, et soitY=OX; rappeler pourquoiPn k=1X2k=Pn k=1Y2k. a) Démontrer queYa même loi queX.PoserX=1n
n X k=1X ketS2=1n1n X k=1 XkX 2: b) En choisissantOdont tous les termes de la dernière ligne sont égaux à1pn vérifier que (n1)S2=nX k=1X 2knX 2=nX k=1Y2kY2n=n1X
k=1Y 2k: c) Déduire de ce qui précède queXetS2sont indépendantes et que(n1)S2 a la même loi quePn1 k=1X2k. Corrigé. Une application orthogonale conserve les longueurs, donc jYj=jOXj. a) Par indépendance des coordonnées, la loi deXest la loi gaus- sienne standardN(0;Id)surRn. Comme transformation linéaire deX,Y=OX est également gaussienne, centrée, de matrice de covariance décrite par E hc;Yi2=Ehc;OXi2=Eh>Oc;Xi2=j>Ocj2=jcj2 pour toutc2Rn. AinsiYest aussi de loiN(0;Id). b) Comme n X k=1 XkX 2=nX k=1X2k2XX
k+X 2=nX k=1X 2knX 2 (c"est une formule de variance!), la première égalité est satisfaite. Par le choix deO,Yn=1pn P n k=1Xk=pnX, d"où la deuxième égalité puisquePn k=1X2k=Pn k=1Y2k. c) PuisqueY= (Y1;:::;Yn)suit la loi gaussienne standardN(0;Id) deRn, les composantesY1;:::;Ynsont indépendantes (de même loiN(0;1)). 4DoncX=1pn
Ynest indépendante dePn1
quotesdbs_dbs2.pdfusesText_3[PDF] exercice corrigé macroéconomie l1
[PDF] exercice corrigé management de projet pdf
[PDF] exercice corrigé math financière pdf les annuités
[PDF] exercice corrigé mécanique cinématique
[PDF] exercice corrigé mémoire cache
[PDF] exercice corrigé méthode abc
[PDF] exercice corrigé méthode abc controle gestion
[PDF] exercice corrigé methode de wilson
[PDF] exercice corrigé microéconomie consommateur pdf
[PDF] exercice corrigé microéconomie l1
[PDF] exercice corrigé microéconomie producteur
[PDF] exercice corrigé microéconomie producteur pdf
[PDF] exercice corrigé microéconomie s1
[PDF] exercice corrigé ms dos
