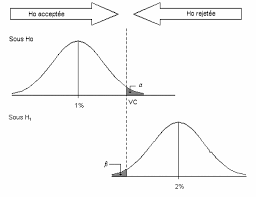
 Exercices corrigés de statistiques inférentielles – Tests dhypothèses
Exercices corrigés de statistiques inférentielles – Tests dhypothèses
Dans un centre de renseignements téléphoniques une étude statistique a montré que l'attente (en secondes) avant que la communication soit amorcée suit une loi
 MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
Si le paramètre de la loi de Student est grand la loi normale peut être utilisée pour Exercices. 1. ⋆Trouver z0.5
 L2 - Psychologie 2019-2020 - Trois exercices sur les tests
L2 - Psychologie 2019-2020 - Trois exercices sur les tests
Corrigé de l'Exercice 1. Lors d'une enquête menée en 2014 sur 450 français Puisque la table de la loi de Student ne donne que des valeurs positives
 Exercices et problèmes de statistique et probabilités
Exercices et problèmes de statistique et probabilités
Corrigés des exercices . Dans cet exercice on s'intéresse à la loi du couple (Yn
 Régression linéaire
Régression linéaire
Exercice 3.10 (Tests) Cet exercice est corrigé en annexe (sujet de décembre 2011). Néanmoins si n ≫ p
 Exercices 10.3 11.1
Exercices 10.3 11.1
13.6
 4-4-Tests corrigés
4-4-Tests corrigés
Sous l'hypothèse H0 la loi de T est la loi de Student à 5 degrés de liberté car le rendement est distribué normalement dans la population. Le seuil de
 Exercice 1 : a) Lecture de la table N(0 1) : X suit une loi normale de
Exercice 1 : a) Lecture de la table N(0 1) : X suit une loi normale de
table de Student `a 10 d.d.l.. ⇒ −t = −2.2281 : F(−t)=0.025 la loi de Student est symétrique. On cherche le fractile t1 tel que : P(T >t1)=0.95 ⇒ F(t1)
 Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Le test de Student suppose que les données sont issues d'une loi normale. Un histo- gramme des 18 différences nous montre une tendance `a la bimodalité mais le
 Leçon 21 Exercices corrigés
Leçon 21 Exercices corrigés
l'exercice). Exercice 4 (Loi de Student). Soient X et Y deux variables indépendantes. X de loi N(0
 Leçon 21 Exercices corrigés
Leçon 21 Exercices corrigés
est appelée loi de Student à n degrés de liberté. Montrer que cette loi a une densité et la décrire (ainsi que son histoire !). Exercice 5. Soient X1
 Feuille de TD 3 : Tests statistiques Exercice 1.
Feuille de TD 3 : Tests statistiques Exercice 1.
On donne le quantile d'ordre 095 pour la loi de Student (10): 1
 Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Corrigé - Série 2 Inférence sur les param`etres Exercice 1 - Les
Le test de Student suppose que les données sont issues d'une loi normale. Un histo- gramme des 18 différences nous montre une tendance `a la bimodalité mais le
 S3 – STATISTIQUES INFERENTIELLES – TD et Exercices
S3 – STATISTIQUES INFERENTIELLES – TD et Exercices
S3 – STATISTIQUES INFERENTIELLES – TD et Exercices CORRIGES. I. LOIS DISCRETES. TD1 : Reconnaître et utiliser une loi hypergéométrique.
 Exercices et problèmes de statistique et probabilités
Exercices et problèmes de statistique et probabilités
Corrigés des exercices . centrale) Lois de probabilités fréquemment utilisées en statistique (Loi normale
 Exercices 10.3 11.1
Exercices 10.3 11.1
13.6
 Cours de Statistiques inférentielles
Cours de Statistiques inférentielles
La loi de Student converge en loi vers la loi normale centrée réduite. Ref : Statistique exercices corrigés
 Exercices corrigés de statistiques inférentielles. Exercice 1 Induction
Exercices corrigés de statistiques inférentielles. Exercice 1 Induction
La variable aléatoire X suit la loi normale N(m ; n ?. ). Or ici ? est inconnu donc il faut utiliser la table de la loi de Student. On cherche la valeur du réel
 Corrigé des exercices
Corrigé des exercices
16?/10?/2013 La loi de Student ne dépend ni de µ ni de la variance. On utilise une loi de Student à n-1 degrés de liberté car elle est équivalente à un ...
 MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
MODULE 7 LOIS PROBABILITÉ PROBABILITÉ
calculer des probabilités sur la loi normale. • utiliser les propriétés de la loi normale pour effectuer des calculs de probabilité. Loi binomiale.
7Lois de probabilité
Les lois de probabilité permettent de décrire les variables aléatoires sous la forme d"une "expérience type» puis d"analyser cette expérience en détail pour pouvoir déduire les principales caractéristiques de toutes les expériences aléatoires qui sont du même type. Letravailestfaituneseulefoismaisilsertàtouteslesexpériencessemblables. L"évaluation delaloideprobabilitéetdescaractéristiquesétanteffectuée, l"utilisateurn"aplusà"con-struire" les probabilités mais simplement à identifier le modèle et à utiliser les résultats
connus sur le modèle. On s"intéressera ici à quelques lois qui sont très fréquentes dans
le domaine de la gestion.Objectifs et compétences
L"étudiant sera en mesure de
calculer des probabilités sur la loi binomiale associer une expérience aléatoire à une loi binomiale calculer des probabilités sur la loi de Poisson associer une expérience aléatoire à une loi de Poisson calculer des probabilités sur la loi exponentielle associer une expérience aléatoire suit à loi exponentielle calculer des probabilités sur la loi normale utiliser les propriétés de la loi normale pour effectuer des calculs de probabilitéLoi binomiale
Considérons l"expérience qui consiste à répéternfois une expérience aléatoire de façon
indépendante telle que le résultat de chaque expérience est un succès ou un échec avec
une probabilité de succèsπ. On peut représenter cette expérience type par la figure2 Chapter 7 Lois de probabilité
suivante : PosonsXla variable aléatoire qui donne le nombre total de succès sur lesntentatives. La variable aléatoireXsuit une loi Binomiale de paramètresnetπ, notéeBin(n,π).Le support de cette variable aléatoire est
SX={0,1,2,···n}
et la loi de probabilité est donnée par f(x) =?n x? x(1-π)n-xpourx= 0,1,2,...n où0< π <1et?n x? =n! x!(n-x)! Les principales caractéristiques numériques sont :Moyenne :E(X) =nπ
Variance :V ar(X) =nπ(1-π)
Ecart type :?
nπ(1-π) Voici un graphique représentant quelques lois binomiales avec une même valeur den, (n= 20) et quelques valeurs deπ.Lois binomiales
x fonction de probabilité0 5 10 15 20
0.0 0.05 0.10 0.15 0.20 0.25
Pi=0.1
Pi=0.25
Pi=0.5
Pi=0.75
Loi binomiale 3
Remarque 7.1Le cas particulier de la loi binomiale avec paramètren= 1etπest à la base de plusieurs modélisation. Il est aussi connu comme étant la loi deBernoulliou expérience de Bernoulli. La notion de succès et d"échec dans le cadre d"une loi binomiale est purement arbitraire. Ainsi, le fait qu"une nouvelle entreprise ne passe pas le cap de la première année peut être qualifié de succès si on s"intéresse au nombre de fermetures tout comme le faitqu"un employé ne soit pas présent au travail une certaine journée peut être un succès si
on veut étudier le taux d"absentéisme. Exemple 7.1?On sait que la probabilité qu"une personne choisie au hasard travaille dans le domaine de l"administration ou de la comptabilité est de 1/6. Si on choisit au hasard 3 personnes, quelle est la probabilité d"avoir au moins 2 personnes sur 3 qui travaillent dans l"administration ou la comptabilité ? Solution :PosonsXla v.a. qui donne le nombre de personnes sur 3 qui travaillent dans l"administration ou la comptabilité,X≂Bin(3,1/6). On cherchePr(X≥2) :Pr(X≥2) =f(2) +f(3)
=?3 2?? 1 6? 2?5 6? 3-2 +?3 3?? 16? 3?5 6? 0 =572+1216= 7.4074×10 -2 = 0.0741 Exemple 7.2?Dans une entreprise les ressources humaines font passer une entrevue préliminaire aux candidats et on sait par expérience que seulement 50% passent au travers de ce premier tri. Quelle est la probabilité que sur 5 candidats, il y en ait 4 ou plus qui passent la première entrevue ? Solution :PosonsXla v.a. qui donne le nombre de candidats sur 5 qui passent la première entrevue,X≂Bin(5,1/2)et on cherchePr(X≥4):Pr(X≥4) =f(4) +f(5)
=?5 4?? 1 2? 4?1 2? 1 +?5 5?? 12? 5 =3164 Chapter 7 Lois de probabilité
Exemple 7.3Les données disponibles sur la survie des entreprises démontrent que les nouvelles entreprises du domaine des communications ont une probabilité de passer le cap des 2 ans de0.20. Si 10 entreprises se sont implantées, quelle est la probabilité d"avoir au moins 4 "survivantes» après 2 ans ? Solution :PosonsXla v.a. qui donne le nombre d"entreprises qui passent le cap des deux ans. C"est une v.a. de loiBin(10,0.2)et on cherchePr(X≥4). OrPr(X≥4) = 1-Pr(X <4) = 1-
3? x=0 fX(x) = 1- 3? x=0 ?10 x? (0.2) x(0.8)10-x = 1-.87913 =.12087 Exemple 7.4?Dans l"exemple précédant, si on sait qu"une entreprise en communi- cation qui passe le cap des 2 ans a une probabilité de2/3de devenir une grande entre- prise(plus de 50 employés), quelle est la probabilité d"obtenir 4 grandes entreprises en communication sur les 10 qui se sont implantées ? Solution:PosonsXlav.a. quidonnelenombred"entreprisessur10quisetransforment en une grande entreprise. C"est une v.a. de loiBin(10,π), oùπest la probabilité qu"une nouvelle entreprise en communication se transforme en une grande entreprise. Pour que la nouvelle entreprise devienne une grande entreprise, il faut qu"elle survive deux ans (disons l"événementA) et qu"elle se transforme en grande une entreprise (dis- ons l"événementB). Orπ= Pr(A∩B) = Pr(A)Pr(B|A)
21023=215puisque la probabilité de passer le cap des 2 ans est de 0.2 par le problème précédantet que la donnée du problème donnePr(B|A) = 2/3.
On a doncX≂Bin(10,
215)et on cherchePr(X≥4). Or
Pr(X≥4) = 1-Pr(X <4) = 1-
3? x=0 fX(x) = 1- 3? x=0 ?10 x?? 2 15? x?13 15? 10-x = 1-.96596 =.03404 Remarque 7.2Pour qu"une variable aléatoire suive une loi binomiale, il faut que lenombre de répétitions de l"expérience soit fixé a priori. De plus, les expériences doivent
Loi binomiale 5
être indépendantes c"est-à-dire que le résultat d"une des expériences n"affecte en aucune
façon les autres. Considérons l"exemple d"une population de 120 entreprises d"un certain secteur et sup- posons que sur ce nombre il y en a 51 qui sont conformes à la norme ISO 9200. Une expérience aléatoire consiste à prendre 15 entreprises au hasard parmi les 120. On veut évaluer la probabilité qu"il y ait au moins 8 entreprises parmi les 15 qui sont conformesà la norme ISO 9200. Même si on répète 15 fois l"expérience consistant à choisir une
entreprise, ce ne sont pas des expériences indépendantes : il n"y a que 120 entreprises et chaque fois qu"une entreprise est choisie à un tirage cela affecte la probabilité au tirage suivant. Exemple 7.5?Un transporteur aérien doit remplir un avion de 330 places. Il vend340 billets en sachant qu"il y a une probabilité de 2.5% qu"un passager ne se présente
pas. Solution :PosonsXla v.a. qui donne le nombre de passagers qui se présenteront sur les 340 billets vendus. On aX≂Bin(340,0.975). Cela veut dire qu"en moyenne il y aura340?0.975 = 331.5passagers par vol. En moyenne il y aura 1.5 passagers qui n"auront pas de place. Comme passager on peut vouloir connaître la probabilité qu"il manque de place. Cela s"exprime parPr(X >330)et en utilisant la formule 1Pr(X >330) =f(331) +f(332) +···+f(340)
=?340331? 0.975331(0.025)340-331+···
= 0.65381 Exemple 7.6?Dans un programme universitaire il y a 30% des étudiants qui dé- passent le temps prévu pour terminer le programme et 10% qui terminent au moins une session avant la fin du temps prévu. On sait que 3% des étudiants qui dépassent le temps ont une cote générale "A", que 20% de ceux qui finissent exactement dans les temps ont cette cote et que ce taux devient 50% pour ceux qui finissent avant. Sur une cohorte de15 étudiants dans le programme quelle est la probabilité qu"il y ait au moins 4 étudiants
avec la cote générale "A" ? Solution :Considérons la v.a.Xqui donne le nombre d"étudiants sur 15 qui auront la cote générale "A". C"est une v.a. qui admet une loi binomiale de paramètresn= 15et π:la probabilité qu"un étudiant au hasard obtienne cette cote. On cherchePr(X≥4). Pour utiliser la fonction de probabilité de la loi binomiale il faut déterminer la valeur du paramètreπ.1Ce calcul peut se faire à la calculatrice mais il est plus simple et surtout plus rapide d"utiliser un logiciel
comme EXCEL.6 Chapter 7 Lois de probabilité
Si on poseB
1:"un étudiant dépasse le temps prévu",B2:"un étudiant termine exacte-
ment dans les délais,B3un étudiant dépasse le temps prévu etA:"obtient la cote A".
L"utilisation de la première règle de Bayes permet d"obtenirπ= 0.179. On a alorsPr(X≥4) = 1-Pr(X <4)
= 1-(f(0) +f(1) +f(2) +f(3)) oùf(x) =? 15 x?0.179x(1-0.179)15-x.L"application de la formule donne
f(0) = 15!0!15!×0.1790×0.82115= 5.1898×10-2
f(1) =15!1!14!×0.1791×0.82114= 0.16973
f(2) = 15!2!13!×0.1792×0.82113= 0.25903
f(3) = 15!3!12!×0.1793×0.82112= 0.24473
et ainsi la probabilité recherchée estPr(X≥4) = 0.27461
Loi de Poisson
La loi de Poisson ou modèle de Poisson permet la modélisation de l"observation d"un phénomènequiproduitdesévénementsàunrythmeconnu. Ons"intéresseàl"observation d"événements et on suppose1. un seul événement arrive à la fois
2. le nombre d"événements se produisant ne dépend que du temps de l"observation
3. les événements sont indépendants
ConsidéronsXla v.a. qui donne le nombre d"événements observés dans une unité de temps. On a alors un phénomène de Poisson et la variable aléatoire qui donne le nombred"événements par unité de temps suit une loi de Poisson, notéeX≂P(λ), oùλest
le nombre moyen d"événements par unité de temps.Loi de Poisson 7
Les valeurs possibles de la variable aléatoire sont SX={0,1,2,...}
et la loi de probabilité est donnée par fX(x) =e
-λλxquotesdbs_dbs18.pdfusesText_24[PDF] exercice corrigé macroéconomie l1
[PDF] exercice corrigé management de projet pdf
[PDF] exercice corrigé math financière pdf les annuités
[PDF] exercice corrigé mécanique cinématique
[PDF] exercice corrigé mémoire cache
[PDF] exercice corrigé méthode abc
[PDF] exercice corrigé méthode abc controle gestion
[PDF] exercice corrigé methode de wilson
[PDF] exercice corrigé microéconomie consommateur pdf
[PDF] exercice corrigé microéconomie l1
[PDF] exercice corrigé microéconomie producteur
[PDF] exercice corrigé microéconomie producteur pdf
[PDF] exercice corrigé microéconomie s1
[PDF] exercice corrigé ms dos
