-;==86E 45 92 fi375 45 1. 0 $ !:29A>5 $ /<@2?8;:> 48ffE=5:?85995> PDF

13 déc. 2011 Remarque : Cette solution générale correspond au mouvement unidimensionnel uniformément accéléré. Exercice 1. ... est une équation de Bernoulli et ...

TDs de mécanique des fluides.

19 sept. 2019 En supposant le fluide parfait et en utilisant la formule de Bernoulli insta- tionnaire (on se reportera `a l'exercice 2.11) entre les deux ...

Mécanique des fluides

théorème de Bernoulli (formule de Torricelli) quel serait le débit initial ... À l'exercice 7

Exercices corrigés

Nous sommes dans les conditions d'applications du théorème de la convergence dominée. D'où le résultat. EXERCICE 1.4.– [Une autre application de la convergence

Énergétique des écoulements Théorème de Bernoulli

25 nov. 2022 11 Vrai homogène à une pression (ou une énergie volumique). Écoulements parfaits. Exercice 2 : Débitmètre de Venturi. 1

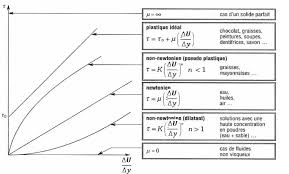MECANIQUE DES FLUIDES: Cours et exercices corrigés

Les équations qui régissent ce type d'écoulement comme l'équation de continuité et l'équation de Bernoulli sont démontrés. Elles sont la base de plusieurs d'

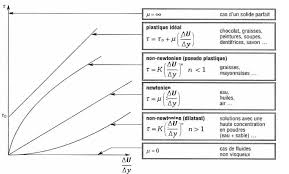MECANIQUE DES FLUIDES: Cours et exercices corrigés

Cours et exercices corrigés. Khalida BEKRENTCHIR. Docteur en Génie des Procédés 4.4.2 Equation de Bernoulli avec échange de travail…………………………………. 4.5 ...

Corrigé du test 1

3 déc. 2018 Exercice 1. Trouver la solution ... Sous quelle forme cherchera-t-on y pour transformer l'équation de Riccati en une équation de Bernoulli?

Équations différentielles

où λµ ∈ R. Correction de l'exercice 11 △. 1. Équation de Bernoulli. (a) On suppose qu'une solution y ne s

MECANIQUE DES FLUIDES. Cours et exercices corrigés

2) Equation de Bernoulli pour un fluide parfait incompressible (avec échange de travail) : v u q. P. ZZg. PP. V. V . ) .(. ) .(. 1. ) (. 2. 1. 1. 2. 1. 2. 2. 1.

Équations différentielles

Résoudre les équations différentielles suivantes en trouvant une solution particulière par la méthode de Exercice 11 Équations de Bernoulli et Riccatti.

Corrigé du test 1

3 déc. 2018 Exercice 1. Trouver la solution générale de l'équation de Bernoulli y/ ?. 3. 4 y = (9x ? 3)y5 dans.

MECANIQUE DES FLUIDES. Cours et exercices corrigés

dynamique des fluides incompressibles parfaits en particulier

MECANIQUE DES FLUIDES: Cours et exercices corrigés

ce type d'écoulement comme l'équation de continuité et l'équation de Bernoulli sont démontrés. Elles sont la base de plusieurs d'applications en hydraulique

Fiche exercices (avec corrigés) - Equations différentielles

Fiche exercices (avec corrigés) - Equations différentielles. Exercice 1. Donner l'ensemble des solutions des équations différentielles suivantes :.

-;==86E 45 92 fi375 45 1. 0 $ !:29A>5 $ /<@2?8;:> 48ffE=5:?85995>

Corrigé de la fiche de TD N° 2 -Analyse 2. Equations différentielles. I. Equations différentielles du 1er ordre. Exercice 1 (Equations différentielles à

COURS hydraulique générale MEPA 2010

ponctuée par une série d'exercices permettant d'illustrer les concepts présentés. Les Après un rappel des équations de Bernoulli le paragraphe suivant ...

MECANIQUE DES FLUIDES I (Cours et Applications) Dr YOUCEFI

Ces quatre chapitres sont illustrés par des exercices résolus qui peuvent aider le Théorème de Bernoulli (écoulement sans échange de travail).

Exercices de Mécanique des Fluides

1- Enoncer le théorème de Bernoulli pour un fluide parfait en précisant la signification des différents termes. 2- Appliquer la relation de Bernoulli entre

REMINI Boualem BENMAMAR Saida

EXERCICE Nº32. Expliquer la montée du niveau d'eau au point A de la figure ci-dessous. A. 1. CORRIGE. En appliquant le théorème de Bernoulli entre les

Comment utiliser le théorème de Bernoulli ?

1- Enoncer le théorème de Bernoulli pour un fluide parfait en précisant la signification des différents termes. 2- Appliquer la relation de Bernoulli entre EXERCICE Nº32. Expliquer la montée du niveau d'eau au point A de la figure ci-dessous. A. 1. CORRIGE. En appliquant le théorème de Bernoulli entre les GP S M .

Quel est le paramètre p de la loi de Bernoulli ?

La loi de Bernoulli de paramètre p désigne une loi de probabilité discrète qui prend la valeur 1 avec la probabilité p et 0 avec la probabilité 1-p. Elle est donc définie sur l’univers ?? = {0,1}.

Qu'est-ce que la loi de Bernoulli ?

C’est l’une des lois de probabilités les plus simples, la loi de Bernoulli est un essentiel à connaitre quand on débute en probabilités La loi de Bernoulli de paramètre p désigne une loi de probabilité discrète qui prend la valeur 1 avec la probabilité p et 0 avec la probabilité 1-p. Elle est donc définie sur l’univers ?? = {0,1}.

Université Oran1 Ahmed Ben Bella

Faculté des Sciences Exactes et Appliquées

LMD-MI- 1

èreannée

2019/2020

Corrigé de la ...che de TD N

1) (x+ 1)y0+y= 0

2)y0sinxycosx= 0

3)y0+xy1x2= 0véri...anty(0) = 1

Solution :

Rappel :

sous la forme : y

0=f(x)g(y)

oùf:I!Retg:J!Rsont deux fonctions continues.

1) (x+ 1)y0+y= 0:::::(E)

Remarque :y= 0est une solution de(E)

siy6= 0: (x+ 1)y0+y= 0()y0=1x+ 1y dydx =1x+ 1y()dyy =1x+ 1dx d"où Zdyy =Z1x+ 1dx=)lnjyj=lnjx+ 1j+C= ln1jx+ 1j+C; C2R =) jyj=1jx+ 1jeC=)y=eC1x+ 1=)y=kx+ 1; k2R

Puisquey= 0est solution de(E)alors :

y=Kx+ 1; K2R 1

2)y0sinxycosx= 0:::::(F)

Remarque :y= 0est une solution de(F)

siy6= 0: y

0sinxycosx= 0()y0=cosxsinxy

dydx =cosxsinxy()dyy =cosxsinxdx d"où Zdyy =Zcosxsinxdx=)lnjyj= lnjsinxj+C; C2R =) jyj=jsinxjeC=)y=eCsinx=)y=ksinx; k2R

Puisquey= 0est solution de(F)alors :

y=Ksinx; K2R:

3)y0+xy1x2= 0.::::(G)

Remarque :y= 0est une solution de(G)

siy6= 0: y

0+xy1x2= 0()y0=x1x2y

dydx =x1x2y()dyy =x1x2dx d"où Zdyy =Z x1x2dx=)lnjyj=12 lnj1x2j+C; C2R =) jyj=pj1x2jeC=)y=eCpj1x2j =)y=kpj1x2j; k2R

Puisquey= 0est solution de(G)alors :

y=Kpj1x2j; K2R On cherche la solution qui véri...e la conditiony(0) = 1: y(0) = 1()K= 1 d"oùy=pj1x2j

1)x(y0yx

)y+x= 0

2)y0(2pxyx) +y= 0, sur]0;+1[véri...anty(1) = 1

Solution :

Rappel :

forme : y 0=fyx oùf:I!Rest une fonction continue.

1)x(y0yx

)y+x= 0::::(E) x(y0yx )y+x= 0()y0= 2yx 1 on poset=yx ()y=tx;doncy0=t0x+t d"oùt0x+t= 2yx

1 = 2t1 =)t0x=t1

ainsit0=1x séparables. doncdtdx =1x (t1)()dtt1=dxx sit16= 0 d"où

Zdtt1=Zdxx

=)lnjt1j= lnjxj+C; C2R =) jt1j=jxjeC=)t1 =eCx=)t=kx+ 1; k2R

Par conséquenty=tx=kx2+x

Les solutions singulières:

sit1 = 0 =)t= 1 =)y=x:c"est la solution singulière de l"équation(E):

2)y0(2pxyx) +y= 0, sur]0;+1[véri...anty(1) = 1::::(F)

0(2pxyx) +y= 0()y0(2ry

1) +yx

= 0 ()y0=yx 2 py x

1avec2ry

x 16= 0

On poset=yx

()y=tx;doncy0=t0x+t d"oùt0x+t=yx 2 py x 1=t2 pt1=)t0x=2tpt 2 pt1 ainsit0=1x 2tpt 2 pt1 séparables. 3 donc dtdx =1x 2tpt 2 pt1 ()2pt12tpt dt=dxx sit6= 0 d"où

Z2pt12tpt

dt=Zdxx =)Z 1t +12tpt dt=Zdxx =) lnt1pt = lnx+C; C2R =)ln(xt) =1pt

C=)xt=e1pt

Par conséquenty=epx

y C

Les solutions singulières:

sit= 0 =)y= 0 :c"est la solution singulière de l"équation(F) On cherche la solution qui véri...e la conditiony(1) = 1 y(1) = 1()e1C= 1()C=1 d"oùy=epx y +1

1)y0+xy=x

2)y0yx

= lnx

3)x(x2+ 1)y02y=x3(x1)ex

Solution :

Rappel :

sous la forme : y

0+a(x)y=b(x)

oùa:I!Retb:I!Rsont deux fonctions continues.

1)y0+xy=x::::::(E)

La solution générale de(E) :yG=yp+y

oùypest une solution particulière de(E) etyest la solution générale de l"équation sans second membre (E0) :y0+xy= 0 On remarque queyp= 1est une solution particulière de(E): 4 On cherche maintenant la solution générale de l"équation sans second membre parables

On remarque quey= 0est solution de(E0):

Siy6= 0 :

0+xy= 0()y0=xy

()dydx =xy()dyy =xdx d"où Zdyy =Z xdx=)lnjyj=x22 +C; C2R =) jyj=ex22 eC=)y=eCex22 =)y=kex22 ; k2R

Puisquey= 0est solution de(E0)alors

y=Kex22 ; K2R Par conséquent la solution générale de(E)est donnée par : y

G=yp+y= 1 +Kex22

; K2R:

2)y0yx

= lnx:::(F)

La solution générale de(F) :yG=yp+y

oùypest une solution particulière de(F) etyest la solution générale de l"équation sans second membre (F0) :y0yx = 0 La solution particulièreypde(F)n"étant pas évidente, on cherche tout d"abord la solution générale de l"équation sans second membre (F0) :y0yx bles

On remarque quey= 0est solution de(F0):

Siy6= 0 :

y 0yx = 0()y0=yx ()dydx =yx ()dyy =dxx d"oùZdyy =Zdxx =)lnjyj= lnjxj+C; C2R =) jyj=jxjeC=)y=eCx=)y=kx; k2R

Puisquey= 0est solution de(F0)alors :

y=Kx; K2R 5 Pour trouver la solution particulière, on appliquela méthode de variation de la constante (MVC).Cette méthode consiste à rem- placer la constanteKpar une fonctionK(x).

On pose :y=K(x)x

alorsy0=K0(x)x+K(x) On remplaceyety0dans l"équation(F)pour obtenirK0(x) : K

0(x)x+K(x)K(x)xx

= lnx=)K0(x) =lnxx =)K(x) =Zlnxx dx

On poseU= lnx=)dU=1x

K(x) =Zlnxx

dx=Z

UdU=U22

+C=(lnx)22 +C; C2R d"oùy=K(x)x=(lnx)22 x+Cx

3)x(x2+ 1)y02y=x3(x1)ex::::::(G)

La solution particulièreypde(G)n"étant pas évidente, on cherche tout d"abord la solution générale de l"équation sans second membre séparables

On remarque quey= 0est solution de(G0):

Siy6= 0 :

x(x2+ 1)y02y= 0()y0=2x(x2+ 1)y dydx =2x(x2+ 1)y()dyy =2x(x2+ 1)dx En décomposant la fraction en éléments simples, on obtient Zdyy =Z2x(x2+ 1)dx=Z 2x 2xx 2+ 1 dx =)lnjyj= 2lnjxj ln(x2+ 1) +C= lnx2x

2+ 1+C; C2R

d"oùy=Kx2x

2+ 1; K2R

Pour trouver la solution particulière, on appliquela méthode de variation de la constante (MVC).Cette méthode consiste à rem- placer la constanteKpar une fonctionK(x).

On pose :y=K(x)x2x

2+ 1 alorsy0=K0(x)x2(x2+ 1) + 2xK(x)(x2+ 1)2 6 On remplaceyety0dans l"équation(G)pour obtenirK0(x) : x(x2+ 1)K0(x)x2(x2+ 1) + 2xK(x)(x2+ 1)22Kx2x

2+ 1=x3(x1)ex

doncK0(x) = (x1)ex=)K(x) =Z (x1)exdx En faisant une intégration par parties on obtient

K(x) =xex+C; C2R

d"oùy=K(x)x2x

2+ 1=(xex+C)x2x

2+ 1=x3exx

2+ 1+Cx2x

2+ 1

1)xy0+y=y2lnx

2) (1x3)y0+ 3x2y=y2

Solution :

Rappel :

forme : y

0+a(x)y=b(x)yk; k2R rf0;1g

oùa:I!Retb:I!Rsont deux fonctions continues. On divise l"équation paryk(y6= 0), ensuite on fait le changement de variablez=y1k

1)xy0+y=y2lnx::::::::(E)

Remarque :y= 0est une solution de(E)

siy6= 0 :

On divise l"équation(E)pary2, on obtient

0y2+y1= lnx::::::::(E0)

On posez=y1, doncz0=y0y2

On remplace dans l"équation(E0);on trouve

d"ordre 1. On résoud cette équation par la méthode de variation de la constante (voir exercice 3), on obtient z=K(x)x= (1x lnx+1x +C)x= lnx+ 1 +Cx; C2R d"oùy=1z =1lnx+ 1 +Cx 7

2) (1x3)y0+ 3x2y=y2:::::::(F)

Remarque :y= 0est une solution de(F)

siy6= 0 :

On divise l"équation(F)pary2, on obtient

(1x3)y0y2+ 3x2y1=1::::::::(F0)

On posez=y1, doncz0=y0y2

On remplace dans l"équation(F0);on trouve

linéaire d"ordre 1. On résoud cette équation par la méthode de variation de la constante (voir exercice 3), on obtient z=K(x)1x3=x+C1x3; C2R d"oùy=1z =1x3x+C

2y0cosx2ysinx=y2:::::::(1)

a)Donner le type de cette équation. b)Trouver la solution générale de(1)

2y0cosx=y2+ 2cos2xsin2x:::::::(2)

c)Véri...er quey0= sinxest une solution particulière de(2): d)En utilisant le changement de variableu=yy0rendre l"équation (2)sous la forme(1):

En déduire la solution générale de(2):

Solution :

Rappel :

forme : y

0+a(x)y=b(x)y2+c(x)

oùa;betcsont des fonctions continues surIR. 8

2y0cosx2ysinx=y2:::::::(1)

a)Donner le type de cette équation. b)Trouver la solution générale de(1)

Remarque :y= 0est une solution de(1)

siy6= 0 :

On divise l"équation(1)pary2, on obtient

2y0y2cosx2y1sinx= 1::::::::(10)

On posez=y1, doncz0=y0y2

On remplace dans l"équation(10);on trouve

linéaire d"ordre1. On résoud cette équation par la méthode de variation de la constante (voir exercice 3), on obtient z=K(x)cosx= (12 tgx+C)cosx=12 sinx+Ccosx; C2R d"oùy=1z

2y0cosx=y2+ 2cos2xsin2x:::::::(2)

c)Véri...er quey0= sinxest une solution particulière de(2): y

0= sinx=)y00= cosx

On remplace dans l"équation(2):2y00cosx=y02+2cos2xsin2x() 2cos

2x= 2cos2x

doncy0= sinxest bien une solution particulière de(2): d)En utilisant le changement de variableu=yy0rendre l"équation (2)sous la forme(1): u=yy0=)y=u+y0=u+ sinx=)y0=u0+ cosx

On remplace dans l"équation(2):

2(u0+ cosx)cosx= (u+ sinx)2+ 2cos2xsin2x

=)2u0cosx2usinx=u2:c"est l"équation(1) Donc la solution générale de cette équation est donnée d"après la questionb)par u=2sinx+Ccosx; C2R d"oùy=u+sinx=2sinx+Ccosx+sinxest la solution générale de(2): 9 coe¢ cients constants)

1)y003y0+ 2y= 0

2)y00+ 2y0+ 5y= 0véri...anty(0) = 0ety0(0) = 1

3)y002y0+y= (x2+ 1)ex

4)y00y0+y= 2x2ex

5)y00y=6cosx+ 2sinx

Solution :

Rappel :

e¢ cients constants s"écrivent sous la forme : y

00+ay0+by=f(x):::::::(E)

oùa;b2Retf:I!Rest une fonction continue. La solution générale de(E)s"écrit sous la forme :y=yp+y0 oùypest une solution particulière de(E)ety0est la solution générale de l"équation sans second membre(E0). y

00+ay0+by= 0::::(E0)est l"équation sans second membre.

2+ar+b= 0:::::(Ec)est l"équation caractéristique.

- Si>0, on a deux racines réellesr1etr2, dans ce cas la solution de(E0)s"écrit sous la forme : y

0=C1er1x+C2er2x; C1;C22R:

- Si = 0, on a une racine doubler, dans ce cas la solution de(E0) s"écrit sous la forme : y

0=C1erx+C2xerx; C1;C22R:

- Si<0, on a deux racines complexes et conjuguéesr=i, dans ce cas la solution de(E0)s"écrit sous la forme : y

0=ex(C1cos(x) +C2sin(x)); C1;C22R:

Résolution de l"équation avec second membre : y

00+ay0+by=f(x)::::(E)

On cherche la solution générale de(E)en utilisant la méthode de variation des constantes. Cette méthode consiste à remplacer les con- stantesC1etC2par des fonctionsC1(x)etC2(x): Soity0=C1(x)y1+C2(x)y2la solution générale de(E0)

On posey=C1(x)y1+C2(x)y2

10 Pour trouverC1(x)etC2(x), on résoud le système suivant :

C01(x)y1+C02(x)y2= 0

01(x)y01+C02(x)y02=f(x)

1)y003y0+ 2y= 0

L"équation caractéristique :r23r+ 2 = 0

= 1 =)r1= 1etr2= 2 doncy0=C1ex+C2e2x; C1;C22R:

2)y00+ 2y0+ 5y= 0véri...anty(0) = 0ety0(0) = 1

L"équation caractéristique :r2+ 2r+ 5 = 0

=16 = 16i2=)r=12i doncy0=ex(C1cos(2x) +C2sin(2x)); C1;C22R: On cherche la solution particulière qui véri...ey(0) = 0ety0(0) = 1 y(0) = 0()C1= 0 doncy0=C2exsin(2x) =)y00=C2exsin(2x) + 2C2excos(2x) y

0(0) = 1()C2=12

d"oùy0=12 exsin(2x)

3)y002y0+y= (x2+ 1)ex::::::(E)

On commence par résoudre l"équation sans second membre y

002y0+y= 0::::::(E0)

L"équation caractéristique :r22r+ 1 = 0

= 0 =)r= 1: racine double doncy0=C1ex+C2xex; C1;C22R On cherche maintenant la solution générale de(E)en utilisant la méthode de variation des constantes. Cette méthode consiste à remplacer les constantesC1etC2par des fonctionsC1(x)etC2(x):

On posey=C1(x)ex+C2(x)xex=C1(x)y1+C2(x)y2

oùy1=exety2=xex Pour trouverC1(x)etC2(x), on résoud le système suivant :

C01(x)y1+C02(x)y2= 0

01(x)y01+C02(x)y02=f(x)

C01(x)ex+C02(x)xex= 0

01(x)ex+C02(x)(x+ 1)ex= (x2+ 1)ex

C01(x) +C02(x)x= 0

01(x) +C02(x)(x+ 1) =x2+ 1

C01(x) =C02(x)x

02(x) =x2+ 1()C01(x) =x3x

02(x) =x2+ 1

d"où 8>< :C

1(x) =x44

x22 +K1 Cquotesdbs_dbs17.pdfusesText_23

[PDF] -;==86E 45 92 fi375 45 1. 0 $ !:29A>5 $ /<@2?8;:> 48ffE=5:?85995>

Comment utiliser le théorème de Bernoulli ?

Quel est le paramètre p de la loi de Bernoulli ?

Qu'est-ce que la loi de Bernoulli ?

Université Oran1 Ahmed Ben Bella

Faculté des Sciences Exactes et Appliquées

LMD-MI- 1

èreannée

2019/2020

Corrigé de la ...che de TD N

1) (x+ 1)y0+y= 0

2)y0sinxycosx= 0

3)y0+xy1x2= 0véri...anty(0) = 1

Solution :

Rappel :

0=f(x)g(y)

1) (x+ 1)y0+y= 0:::::(E)

Remarque :y= 0est une solution de(E)

Puisquey= 0est solution de(E)alors :

2)y0sinxycosx= 0:::::(F)

Remarque :y= 0est une solution de(F)

0sinxycosx= 0()y0=cosxsinxy

Puisquey= 0est solution de(F)alors :

3)y0+xy1x2= 0.::::(G)

Remarque :y= 0est une solution de(G)

0+xy1x2= 0()y0=x1x2y

Puisquey= 0est solution de(G)alors :

1)x(y0yx

2)y0(2pxyx) +y= 0, sur]0;+1[véri...anty(1) = 1

Solution :

Rappel :

1)x(y0yx

1 = 2t1 =)t0x=t1

Zdtt1=Zdxx

Par conséquenty=tx=kx2+x

Les solutions singulières:

2)y0(2pxyx) +y= 0, sur]0;+1[véri...anty(1) = 1::::(F)

0(2pxyx) +y= 0()y0(2ry

1) +yx

1avec2ry

On poset=yx

Z2pt12tpt

C=)xt=e1pt

Par conséquenty=epx

Les solutions singulières:

1)y0+xy=x

2)y0yx

3)x(x2+ 1)y02y=x3(x1)ex

Solution :

Rappel :

0+a(x)y=b(x)

1)y0+xy=x::::::(E)

La solution générale de(E) :yG=yp+y

On remarque quey= 0est solution de(E0):

Siy6= 0 :

0+xy= 0()y0=xy

Puisquey= 0est solution de(E0)alors

G=yp+y= 1 +Kex22

2)y0yx

La solution générale de(F) :yG=yp+y

On remarque quey= 0est solution de(F0):

Siy6= 0 :

Puisquey= 0est solution de(F0)alors :

On pose :y=K(x)x

0(x)x+K(x)K(x)xx

On poseU= lnx=)dU=1x

K(x) =Zlnxx

UdU=U22

3)x(x2+ 1)y02y=x3(x1)ex::::::(G)

On remarque quey= 0est solution de(G0):

Siy6= 0 :

2+ 1+C; C2R

2+ 1; K2R

On pose :y=K(x)x2x

2+ 1=x3(x1)ex

K(x) =xex+C; C2R

2+ 1=(xex+C)x2x

2+ 1=x3exx

2+ 1+Cx2x

1)xy0+y=y2lnx