 Rotations 3D et Quaternions
Rotations 3D et Quaternions
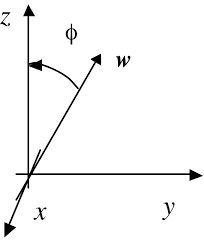
Rotation d'un angle ϑ autour de l'axe w page. 016. Page 17. Dr Mohamed Bouri 2018. Passage Axe/Angle => Matrice de cos. dir. (10). R =(1-cosϑ) xx xy xz xy yy
 Chapitre 5 : Transformations et changements de repères - Master
Chapitre 5 : Transformations et changements de repères - Master
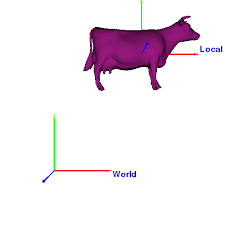
Rotation 3D : autres axes. ROX =.. 1. 0. 0. 0 cosθ −sinθ. 0 sinθ cosθ Exemple : rotation d'axe quelconque. ▷ Avec un objet défini localement dans ...
 Transformations géométriques : rotation et translation
Transformations géométriques : rotation et translation
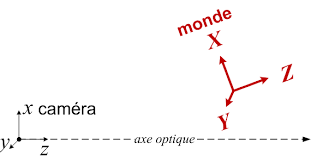
rotation autour axe y rotation autour axe x rotation autour axe z. 1 0 0. 0 1 0. 0 0 1. 0 0 0 1 x y z. T. T. T. T. ⌈. ⌉. │. │. │. │. = │. │. │. │. ⌊.
 Rotation dans lespace 3D
Rotation dans lespace 3D
Le vecteur colinéaire à l'axe autour duquel la rotation est effectuée a pour composantes Lorsque l'on dispose d'une matrice de rotation quelconque rappelons ...
 Rappels mathématiques Transformations géométriques 2D et 3D 1
Rappels mathématiques Transformations géométriques 2D et 3D 1
autour d'un point quelconque voir la section. “Composition de transformations ... On peut maintenant écrire la matrice de la rotation autour de l'axe Y : (EQ ...
 LES ROTATIONS DE R3 : VERSION MATRICIELLE 1. Lespace R
LES ROTATIONS DE R3 : VERSION MATRICIELLE 1. Lespace R
est une solution non nulle et l'axe de la rotation de matrice B est engendré par le vecteur de Soit Ru
 Quaternions orientation et mouvement
Quaternions orientation et mouvement
Oct 17 2017 Porte tournée d'un angle θ autour d'un axe dirigé par −→k. Angles d'Euler (zxz) (θ
 IMN428 - Chapitre 2 - Transformations géométriques
IMN428 - Chapitre 2 - Transformations géométriques
Jan 22 2014 Contrairement à la rotation dans le plan
 Chapitre II - Transformations de corps rigides
Chapitre II - Transformations de corps rigides
Un carré après avoir subi une rotation autour d'un axe quelconque et une translation la position finale de l'objet selon une matrice de rotation 3 x 3 suivie ...
 ME 5.1a
ME 5.1a
Nov 9 2020 l'axe y d'un angle et la matrice de rotation autour de l'axe x d'un angle ... dans l'espace 3D autour d'axes arbitraires γ β. Rotations ...
 Transformations géométriques : rotation et translation
Transformations géométriques : rotation et translation
de B selon les axes de B
 Chapitre II - Transformations de corps rigides
Chapitre II - Transformations de corps rigides
Plusieurs transformations appliquées aux objets 3D peuvent être Un carré après avoir subi une rotation autour d'un axe quelconque et une translation.
 IMN428 - Chapitre 2 - Transformations géométriques
IMN428 - Chapitre 2 - Transformations géométriques
Jan 22 2014 Transformations affines 3D. 5. Gestion des matrices dans OpenGL ... dans le plan
 Rotation dans lespace 3D
Rotation dans lespace 3D
Le vecteur colinéaire à l'axe autour duquel la rotation est effectuée a pour La matrice de rotation dans la base quelconque C s'exprime de manière ...
 LES ROTATIONS DE R3 : VERSION MATRICIELLE 1. Lespace R
LES ROTATIONS DE R3 : VERSION MATRICIELLE 1. Lespace R
Rappelons les produits scalaire et vectoriel le déterminant (de matrices 2 Comme u et ?u engendrent le même axe Ru
 QUATERNION
QUATERNION
Convertir des matrices de rotation et des quaternions v un vecteur 3D. ... ? autour d'un axe de rotation v unitaire quelconque.
 ÉTUDE DE LÉQUILIBRE DES CORPS
ÉTUDE DE LÉQUILIBRE DES CORPS
Le corps a tendance à tourner horaire autour de "O". On calcul toujours un moment par rapport à un axe de rotation quelconque exemple l'axe "O" on notera
 PHQ114: Mecanique I
PHQ114: Mecanique I
May 30 2018 Rotation des axes cartésiens d'un angle ? autour de l'axe z. ex ey e x e y ?. A. Ax. Ay. A x. A y. Un vecteur A quelconque peut s'exprimer ...
 RAPPORT DE PROJET DE FIN DÉTUDES Aleksander Przybylo
RAPPORT DE PROJET DE FIN DÉTUDES Aleksander Przybylo
Matrice de rotation. Une fonction spéciale a été implantée qui permet de créer une matrice de rotation autour d'un axe quelconque :
 ANIMATION BASÉE SUR LINTERPOLATION
ANIMATION BASÉE SUR LINTERPOLATION
Ð Déplacement sur un axe 3D: É Le modèle contient un nombre de frame réduit pour l'animation. ... Ð Rotation autour d'un axe quelconque.
 Rotation en trois dimensions
Rotation en trois dimensions
Commençons par faire une rotation d’axe Oz et d’angle ? Dans un repère orthonormé Oxyz cela revient à faire une rotation plane dans le plan xOy ou dans un plan parallèle tout en laissant fixes les points de l’axe Oz Cette rotation a pour matrice cos sin 0 sin cos 0 0 0 1 R ? ? ? ? ? =
Qu'est-ce que la matrice de rotation ?
Ces dernières sont aussi appelées rotations vectorielles (d'où le nom de « matrice de rotation »), parce qu'en dimension 2 et 3, elles correspondent respectivement aux rotations affines planes autour de l'origine et aux rotations affines dans l'espace autour d'un axe passant par l'origine.
Comment calculer la rotation d'une matrice ?
Ainsi, à partir de n'importe quelle matrice de rotation 3×3, on peut déterminer un axe et un angle, et ceux-ci déterminent complètement la rotation (à l'orientation près). Une matrice de rotation 2×2 a nécessairement la forme suivante : avec a2 + b2 = 1. Nous pouvons donc poser a = cos ? et b = sin ?, pour un certain angle ?.
Qu'est-ce que la rotation en dimension supérieure à 3 ?
Mais en dimension supérieure à 3, le fait nouveau est qu'une rotation n'est pas nécessairement de cette forme (i.e. le sous-espace de ses vecteurs fixes peut très bien être de dimension strictement inférieure à n –2) : c'est seulement un produit de rotations de cette forme (cf exemples ci-dessous). correspond à une rotation de 90° dans le plan.
Comment interpréter une matrice de rotation ?
L'interprétation d'une matrice de rotation peut donner naissance à plusieurs ambiguïtés : La modification des coordonnées d'un vecteur peut correspondre à une rotation de ce vecteur ( alibi ), ou à une rotation du repère ( alias ). La matrice peut représenter la rotation dans un repère orienté positivement ou négativement.
Chap. 3: Étude de l'équilibre des corps GC2
3ÉTUDE DE L'ÉQUILIBRE DES CORPS
3.1 MOMENT D'UNE FORCE
3.1.1 Introduction
Un corps n'est pas seulement en équilibre que
lorsque la somma tion des forces est nulle. Par exemple, dans la figure ci-contre, la force résultante est nulle. Par contre, ce corps n'est pas en équilibre car il peut tourner. Ceci nous amène à définir un autre concept que la force pour étudier l'équilibre statique des corps. Ce concept fait appel à la notion de moment de force.En effet, dans l'étude de l'
équilibre des corps les notions de grandeur, direction et sens des forces sont importantes mais une quatrième l'est tout aussi; celle du point d'application des forces. 10 N 10 NFig. 3.1
3.1.2 Définition
Lorsque l'on veut ouvrir une porte,
on tire sur la poignée en espérant que la porte effectue un mouvement de rotation autour de ses charnières.Cependant, qu'arriverait-il si la
poignée était située au centre de la porte? Évidemment, la porte serait plus difficile à ouvrir.Charnières
(axe de rotation)l/2l/2100 N100N
100 NAB C
Fig. 3.2
26 STATIQUE ET RÉSISTANCE DES MATÉRIAUX
GC2 Chap. 3: Étude de l'équilibre des corps
En observant la figure 3.2 on peut voir que pour une même force, l'efficacité à ouvrir la porte n'est
pas la même. On peut dire qu'il serait plus facile d'ouvrir la porte avec la force B que la A ou la C.
Avec cet exemple on voit bien l'importance du point d'application de la force.On définira donc le moment d'une force comme:
"l'efficacité d'une force à produire une rotation par rapport à un point".Le moment de force est une quantité vectorielle mais nous n'en tiendrons pas compte complètement
dans notre étude de la statique. C'est la grandeur du moment ainsi qu'un signe + ou - qui le définira.
Le signe du moment sera déterminé par rapport à une convention que l'on verra plus loin.3.1.3 Calcul du moment
Si on observe cet autre exemple, on s'apperçoit que pour un même point d'application ce n'est pas nécessairement toute la force qui produit la rotation. Ainsi, la composante horizontale de la force A x ne produit aucune rotation par rapport à l'axe de rotation que représente les charnières. Par contre, la composante verticale de la force A y produit à elle seule "toute" la rotation.Charnières
(axe de rotation) A A x A y r h OFig. 3.3
À partir de ces observations on peut définir de façon opérationnelle le moment d'une force par
rapport à un axe de rotation comme étant: "Le produit de la grandeur de la force multipliée par la distance entre sa ligne d'action et l'axe de rotation considéré"Note importante, la distance ou bras de levier est mesurée perpendiculairement à la ligne d'action
de la force.STATIQUE ET RÉSISTANCE DES MATÉRIAUX27
Chap. 3: Étude de l'équilibre des corps GC2
On calcule le moment de la force par rapport à l'axe de rotation "O" de la figure 3.3 comme: M o = Force x bras de levier (perpendiculaire) = A x h (3.1)Pour le calcul du moment à partir d'un dessin (méthode graphique), cette méthode est relativement
facile à utiliser. Cependant, pour le calcul analytique du moment, il est parfois difficile de calculer le
"bras de levier" h. On note toujours le moment M indicé de l'axe de rotation "O" par rapport à lequelle on mesure le moment i.e. M o À partir des lois de la trigonométrie on peut déduire que: h = r sinDonc M
o = A x r sin (a) De même, si on observe les composantes de A, on a vu que: A x = A cos A y = A sinComme on voit et comme on a défini, le moment de la force est le produit de la force multipliée par
le bras de levier mesuré perpendiculairement.La composante horizontale de A (A
x ) ne possède pas de bras de levier (sa ligne d'action passe par "O"; h = 0) donc son moment est nécessairement égal à 0 aussi . La composante verticale de A (A y ) est déjà perpendiculaire au bras de levier "r" donc son moment est égal à: M o = A y x rComme A
y = A sin alors: M o = A sin x r (b) La comparaison des équations (a) et (b) nous montre qu'elles sont identiques. Et comme le momentdû à la composante horizontale est égal à zéro donc la somme des moments des composantes nous
donne le même résultat. On peut donc conclure que:28 STATIQUE ET RÉSISTANCE DES MATÉRIAUX
GC2 Chap. 3: Étude de l'équilibre des corps
"Le moment d'une force peut être calculé par la somme des moments des composantes de cette force". Les unités du moment d'une force sont: Force [N] x bras de levier [m] donc des [Nm]. On utilisera aussi comme convention de signe (puisque comme on l'a vu précédemment, le moment est un vecteur) que lorsque la force aura tendance à faire tourner anti-horaire un corps autour d'un axe quelconque son moment sera + alors que s'il a tendance à tourner horaire ce moment sera -. Cette convention sera utile lorsque l'on calculera le moment total ou résultant sur un corps. Il est à noter que certains auteurs utilisent d'autres conventions (ex: convention inverse ouchangement de convention à chaque cas ou autre ...) mais pour simplifier le language et avoir tous la
même terminologie on conservera cette convention jusqu'à la fin.En résumé:
Moment d'une force (M
o ) = force x bras de levier (perpendiculaire) [Nm] ou moments des composantes de cette forceMoment résultant (M
0 ) = des moments de chacune des forces ou des moments des composantes des forces M o (+) => Le corps a tendance à tourner anti-horaire autour de "O" M o (-) => Le corps a tendance à tourner horaire autour de "O" On calcul toujours un moment par rapport à un axe de rotation quelconque, exemple l'axe "O" on notera alors le moment M oSTATIQUE ET RÉSISTANCE DES MATÉRIAUX29
Chap. 3: Étude de l'équilibre des corps GC2
3.2 COUPLE
3.2.1 Définition
Dans la pratique, on retrouve plusieurs
exemples de couples; lorsqu'on ouvre un robinet ou lorsqu'on visse un écrou, on exerce un couple.On définit le couple comme étant:
F F dFig. 3.4
Un système de deux forces parallèles, d'égales grandeurs, de sens opposé s et de lignes d'action différentes. La distance perpendiculaire "d" séparant les deux forces s'appelle bras de levier du couple.3.2.2 Valeur du couple
Le moment du couple est égal à la grandeur de l'une des forces par la distance (mesurée perpendiculairement) entre leurs lignes d'action.M = Fd (3.2)
Le moment du couple est indépendant de l'axe de rotation considéré. Comme par exemple dans la figure ci-contre le moment est donné par: - F x d.(horaire) Vérifions en calculant le moment résultant de ces deux forces du couple par rapport aux trois axes de rotation A,B et C.
M A = Fs - F(s + d)Fs - Fs - Fd = -Fd
d s h 2d/3 A B C F FFig. 3.5
30 STATIQUE ET RÉSISTANCE DES MATÉRIAUX
GC2 Chap. 3: Étude de l'équilibre des corps
M B = -Fd/3 - F2d/3 = -Fd M C = Fh - F(h + d)Fh - Fh - Fd = -Fd
On voit très bien que quelque soit l'axe de rotation, le moment du couple est le même et vaut la
grandeur de la force multipliée par la distance les séparant.3.2.3 Couples équivalents
Deux couples sont équivalents s'ils ont le même moment (grandeur et sens); on peut donc lesremplacer en tout temps sans changer l'effet produit sur le corps. Si on observe la figure ci-dessous,
on a un exemple de trois couples équivalents, on peut alors voir l'importance du "bras de levier". On
produit exactement la même rotation avec une force F espacée d'une distance d qu'avec une force
coupée de moitié F/2 espacée du double (2d). F d 2d F 2 F 2 d/2 2F 2FFig. 3.6
Dans chacun des cas illustrés à la figure 3.6 le moment vaut -Fd (- car horaire).3.3 PRINCIPES GÉNÉRAUX DE LA STATIQUE
3.3.1 Premier principe
On peut faire glisser une force sur sa ligne d'action, sans changer son effet sur un corps. Ce principe est appelé théorème du glisseme nt.STATIQUE ET RÉSISTANCE DES MATÉRIAUX31
Chap. 3: Étude de l'équilibre des corps GC2
F FFig. 3.7
3.3.2 Deuxième principe
La ligne d'action de la résultante d'un système de force concourantes doit passer nécessairement par le point de rencontre des lignes d'action de ces forces. A CLigne d'action
de la résultante (parallèle à R)Intersection des
lignes d'action B A B C RFig. 3.8
32 STATIQUE ET RÉSISTANCE DES MATÉRIAUX
GC2 Chap. 3: Étude de l'équilibre des corps
3.3.3 Troisième principe
On peut remplacer plusieurs forces quelconques par leur résultante sa ns changer leur effet sur un corps. (voir aussi fig. 3.8)Fig. 3.9
3.3.4 Quatrième principe
On peut appliquer en un point quelconque d'un corps deux for-ces égales et directement opposées sans déranger l'état de ce co rps. F F F FFig. 3.10
STATIQUE ET RÉSISTANCE DES MATÉRIAUX33
Chap. 3: Étude de l'équilibre des corps GC2
3.3.5 Cinquième principe
Lorsqu'un corps A exerce une force sur un corps B, celui-ci exerce toujours sur le corps A une force égale en grandeur mais directement opposée. On appelle ce principe action et réaction. P N NP A B F AB F BAFig. 3.11
La force F
AB (force exercée sur A par rapport à B) serait l'action tandis que la force F BA (forceexercée sur B par rapport à A) la réaction. L'action et la réaction sont des forces s'exerçant toujours
en paires.quotesdbs_dbs44.pdfusesText_44[PDF] page de garde mémoire word
[PDF] page de garde télécharger
[PDF] page de garde modèle
[PDF] page de garde mémoire master
[PDF] page de garde mémoire de fin d'étude
[PDF] page de garde de technologie ? imprimer 5eme
[PDF] page de garde technologie 6ème
[PDF] page de garde technologie 4eme
[PDF] page de garde cahier du jour
[PDF] pages de garde ce2
[PDF] page de garde cahier cycle 3
[PDF] bled anglais études supérieures pdf
[PDF] bled anglais grammaire pdf
[PDF] telecharger cours de grammaire anglaise pdf
