 Validation et optimisation dune décomposition hiérarchique de
Validation et optimisation dune décomposition hiérarchique de
24 janv. 2012 Dans ce cadre une généralisation de cette mesure de qualité au cas multi-niveaux est introduite. Nous testons notre méthode sur des graphes ...
 CHAPITRE 2 : Théorie des graphes et applications
CHAPITRE 2 : Théorie des graphes et applications
une marque `a chaque sommet du graphe ordonné en niveaux. a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur
 Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
graphe niveau par niveau à partir d'un sommet donné ;. – le parcours en ... Un projet est généralement décomposé en différentes tâches à effectuer. Chaque ...
 GRAPHES
GRAPHES
2 avr. 2008 Graphes sans circuit. Lorsque le graphe est sans circuit il peut être décomposé en niveaux. La longueur du chemin de la racine `a tous les ...
 Décomposition algorithmique des graphes
Décomposition algorithmique des graphes
23 mai 2007 composition en branches d'un hyper-graphe planaire une décomposition de ... au niveau de ses extrémités et uniquement à cet endroit. Comme une ...
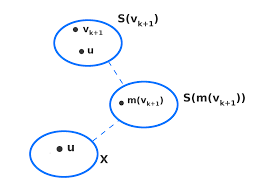 Étude dalgorithmes de décomposition de graphes
Étude dalgorithmes de décomposition de graphes
1 sept. 2020 Il nous faut aussi définir la famille des graphes chordaux car ils sont étroitement liés aux tree-decompositions. Étant donné un graphe G un ...
 Théorie des graphes DUT Informatique semestre 2
Théorie des graphes DUT Informatique semestre 2
3 févr. 2014 courts dans un graphe il faut donc savoir décomposer un graphe en niveaux. È2.8 Décomposition en niveau d'un graphe sans circuit : 1. 2. 3. 4.
 Chapitre 6 Décompositions arborescentes†
Chapitre 6 Décompositions arborescentes†
sans arêtes communes et ces sous-graphes sont « recollés » au niveau de leurs Nous venons de définir un opérateur de décomposition d'un graphe en deux sous- ...
 Les plans dexpériences par la méthode TAGUCHI
Les plans dexpériences par la méthode TAGUCHI
niveaux décomposé en nombre premier (l'interaction BC à 6 niveaux a été Pour construire 2 colonnes à 4 niveaux il faut partir d'un graphe linéaire.
 Théorie des graphes
Théorie des graphes
7 avr. 2011 S-séquence d'un graphe - Décomposition par niveaux. 5 Probl`eme du plus court chemin. L. Sais (Algorithmique & Programmation 5).
 Corrigé TD1 13-14
Corrigé TD1 13-14
À partir de ces listes on obtient la décomposition par niveaux : S0 = {E H}
 CHAPITRE 2 : Théorie des graphes et applications
CHAPITRE 2 : Théorie des graphes et applications
a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur maximale au sens des arcs allant de.
 Table des matières
Table des matières
2 Décomposition des graphes Décomposition basée sur la matrice de la fermeture transitive ... décomposition d'un graphe sans circuit en niveaux.
 Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
le parcours en largeur consiste à explorer les sommets du graphe niveau par Un projet est généralement décomposé en différentes tâches à effectuer.
 Théorie des graphes DUT Informatique semestre 2
Théorie des graphes DUT Informatique semestre 2
3 fév. 2014 Pour décomposer en niveau un graphe G on utilisera l'algorithme suivant : ... il faut donc savoir décomposer un graphe en niveaux.
 Quelques propriétés des graphes distances héréditaires
Quelques propriétés des graphes distances héréditaires
6.3.1 Rappels sur la décomposition par substitution . . . . . 26. 6.3.2 Pour les graphes 2 – Un exemple de graphe avec les niveaux de distances.
 Structure multi-échelle de grands graphes de terrain
Structure multi-échelle de grands graphes de terrain
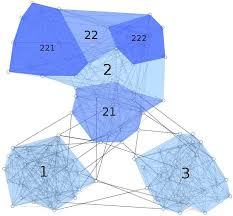
Graphe avec représentation de la décomposition niveau par niveau et de l'arbre obtenu. Les feuilles de l'arbre sont les sommets du graphe initial.
 Méthodes dOptimisation
Méthodes dOptimisation
1.1.2 Niveaux des sommets d'un graphe sans circuit . Le mouvement de mati`ere se décompose en un nombre fini de mouvements partiels chacun allant d'un.
 PLANIFICATION et Ordonnancement
PLANIFICATION et Ordonnancement
Les rangs (ou niveaux) déterminés permettent de positionner le début des différentes tâches lors de la construction du graphe.
 IT3004 Graphes et algorithmes Notes de cours et exercices - ESIEE
IT3004 Graphes et algorithmes Notes de cours et exercices - ESIEE
Exemple 1 : Soit un graphe G=(E?) avec E ={1234}et ? dé?nie par : ?(1)={124} ?(2)={31} ?(3)={4} ?(4)=0/ Iln’estpasfaciledevisualiserungraphedonnésouscetteforme Habituellementonreprésente ungrapheparundessintelqueceluidela?gure1 1pagesuivante Notonsqueplusieursdessins comme pour cet exemple peuvent représenter le même
 Les graphes - univ-reunionfr
Les graphes - univ-reunionfr
De manière générale un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication réseaux routiers interaction de diverses espèces animales circuits électriques )
 Théorie des graphes et optimisation dans les graphes - CNRS
Théorie des graphes et optimisation dans les graphes - CNRS
i(dans le cas d’un 1-graphe on aura d +(s i) =jsucc(s i) j) De même le demi-degré intérieur d’un sommet s i noté d (s i) est le nombre d’arcs arrivant à s i(dans le cas d’un 1-graphe on aura d (s i) =jpred(s i) j) Exercice : Dessiner un graphe non orienté complet à 4 sommets Quel est le degré des som-mets de ce graphe?
 Chapitre 3 - Graphes 1 Graphes et modes de représentation
Chapitre 3 - Graphes 1 Graphes et modes de représentation
Pour le rendre plus lisible il est souvent utile de représenter un graphe par niveaux Pour cela il faut déterminer le niveau de chacun des sommets du graphe Proposition Le niveau d'un sommet a autv : 0 si a n'a pas de prédécesseur 1+nmax sinon où nmax est le maximum des niveaux des prédécesseurs de a Méthode
 Searches related to décomposition d+un graphe en niveaux PDF
Searches related to décomposition d+un graphe en niveaux PDF
La treelength d’un graphe est elle aussi toujours dé?nie : la length de la décomposition constituée d’un seul sac contenant tous les sommets du grapheestégaleaudiamètredugraphe(ladistanceentrelesdeuxsommets lespluséloignés)unebornesupérieuredelatreelength Figure 5–Ungrapheetunetree-decompositiondecegraphe
Quel est le degré d’un graphe?
3.b Ordre et degré On appelleordred’un graphe le nombre de ses sommets. Ledegréd’un sommet est le nombre d’arrêtes dont il est une extrémité. Deux sommets reliés par une même arrête sont ditsadjacents.
Quel est le degré d’un graphe d’ordre 4?
b D Ce graphe comporte 4 sommets, c’est donc un graphe d’ordre 4. • Du sommet A partent 4 arrêtes. Le degré du sommet A est donc 4. • Le degré du sommet B est 3. • Le degré du sommet C est 4. • Le degré du sommet D est 1.
Quels sont les problèmes des graphes pondérés?
J 10 25 97 12 30 39 17 L’un des problèmes classiques des graphes pondérés est celui de recherche d’un trajet routier le plus court (en terme de temps ou de kilomètres). Si un graphe n’est pas pondéré, le poids de chaque arête peut être considéré comme égale à 1.
Quel est le rôle d'un graphe?
De manière générale, un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication, réseaux routiers, interaction de diverses espèces animales, circuits électriques...)
Th´eorie des graphes
L. Sais
Algorithmique & Programmation 5
7 avril 2011
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 1 / 1251Graphe et algorithme : pr´esentation
Introduction
D´efinitions et terminologie
Repr´esentation
Matrice d"adjacence
Listes d"adjacence
2Parcours, num´erotation et descendance
3Connexit´e et forte connexit´e
4Graphes sans circuit
5Probl`eme du plus court chemin
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 2 / 125 Graphes et algorithme : pr´esentationIntroduction De nombreux probl`emes courants, en informatique, en ing´enierie, en sciences sociales, en intelligence artificielle, peuvent se repr´esenter en termes de relations (binaires) entre objets.On peut citer par exemple :
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 3 / 125 r´eseaux de communications: routiers, ferroviaires, machines en r´eseaux, circuits int´egr´es, ... L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 4 / 125 On distingue les sommets(villes, carrefours, soudures) et les arcsou arˆetes (communication entre sommets) qui mettent en relation les sommets. On associe parfois aux arcs des caract´eristiques, qui permettent d"exprimer des distances, des coˆuts, des flux, ... Le type des probl`emes que l"on peut se poser alors concerne par exemple la recherche d"itin´eraires optimaux (probl`eme classique du voyageur de commerce : visiter toutes les villes avec un cheminement optimal). L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 5 / 125 relations sociales: familiales, hirarchiques, d"incompatibilit´e, ... Ici, les sommets correspondent aux individus, les arcs aux relations entre individus. ordonnancement de tˆaches: atelier, systmes d"informations, ... Une premi`ere possibilit´e consiste repr´esenter les instants de d´ebut et de fin d"activit´e par les sommets, et les activit´es par les arcs; on peut ´egalement repr´esenter les tˆaches par les sommets et les relations de pr´ec´edance par les arcs. L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 6 / 125 18 263 54 7 9
1 : cale¸con 4 : veste 7 : chemise
2 : pantalon 5 : cravate 8 : chaussures
3 : ceinture 6 : chaussettes 9 : montre
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 7 / 125 repr´esentation d"algorithmes(organigrammes) : Les sommets correspondent aux instructions ou tests, les arcs correspondent aux enchanements possibles entre instructions ou tests.On retrouvera ´egalement :
* les emplois du temps * les automates `a ´etats finis * les probl`emes de coloration de cartes (2 pays voisins doivent avoir 2 couleurs diff´erentes) * etc. L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 8 / 125Remarque
Le formalisme des graphes permet de d´ecrire de nombreux probl`emes souvent de mani`ere simple, mais qui peuvent s"av´erer difficile `a r´esoudre. Dans le cadre de ce cours, on traitera des probl`emes classiques o`u de bons algorithmes sont connus (il existe des probl`emes o`u l"on ne connait pas de bons algorithmes) : ´etant donn´e un graphe, v´erifier s"il poss`ede certaines propri´et´es ´etant donn´e un graphe, d´eterminer une partie poss´edantcertaines propri´et´es. construire un, plusieurs, ou tous les graphes poss´edant certaines propri´et´es. L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 9 / 125 Graphes et algorithme : pr´esentationD´efinitions et terminologieD´efinition
Un graphe orient´eest un couple G=(S,A) o`u :
- S est un ensemble fini d"´el´ements appel´es sommets - A est un ensemble fini de couples de sommets appel´es arcs on a A?S×SRemarque
S"il existe plusieurs arcs entre deux sommets, on parle d"unmultigraphe (arcs multiples) L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 10 / 125Exemple
63 4215
7 8S={1..8}
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 11 / 125D´efinitions
Etant donn´e un graphe G=(S,A) etx?S
si (x,y)?A, alorsyest un successeurdex si (y,x)?A, alorsyest un pr´ed´ecesseurdex xetysont adjacentssiyest un pr´ed´ecesseur et/ou un successeur de x l"ensemble des successeursdexest not´e Γ+(x) +(x) ={y|(x,y)?A} l"ensemble des pr´ed´ecesseursdexest not´e Γ+(x) -(x) ={y|(y,x)?A} l"ensemble des voisinsdexest not´e Γ(x)Γ(x) = Γ+(x)?Γ-(x)
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 12 / 125 le degr´e int´erieurdexest not´e d-(x) d -(x) =|Γ-(x)| le degr´e ext´erieurdexest not´e d+(x) d +(x) =|Γ+(x)| le degr´edexest not´e d(x) d(x) =|Γ(x)|D´efinition
Un graphe non orient´eest un couple G=(S,A) o`u : - S est un ensemble fini d"´el´ements appel´es sommets - A est un ensemble fini de paires de sommets appel´es arˆetesUne arˆete est not´ee{x,y}
Dans le cas de ces graphes non-orient´es, on parle simplement de sommets voisins et de degr´e. L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 13 / 125Exemple
63 4215
87S={1..8}
A={{3,5},{4,5},{3,4},{6,7},{8,7}}
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 14 / 125D´efinition (graphe complet)
Un graphe orient´e G=(S,A) est dit completsi A=S2 Un graphe non orient´e G=(S,A) est dit completsi toute paire de sommets figure dans AD´efinition
Etant donn´e un graphe orient´e G=(S,A) :
le graphe r´eciproque de Gest le graphe G-1=(S,A-1) o`u A -1={(x,y)?S×S|(y,x)?A} le graphe sym´etris´eassoci´e `a G est le graphe GS=(S,A?A-1)D´efinition
Un graphe valu´eest un graphe orient´e ou non orent´e G=(S,A) auquel on associe une fonction de coˆut c : A->R , un tel graphe est not´e (S,A,c) L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 15 / 125Exemple
Voir l"exemple sur le r´eseau routier (villes)
Notations
Si G=(S,A) On a|S|=card(S)=n et|A|=card(A)=m
Rapports etre n et m
: (cas des graphes orient´es)Si G=(S,A) n"est pas un multigraphe, on a A?S2
graphes tels que m=n2: graphes complets avec boucles graphes complets sans boucle : m=n(n-1) L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 16 / 125Relations entre d+, d-, d et m:
pour le cas des graphes orient´es sans boucles : x?Sd +(x) =? x?Sd -(x) =1 2? x?Sd(x) =m pour le cas des graphes non orient´es : x?Sd(x) = 2m L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 17 / 125D´efinition
Etant donn´e un graphe orient´e G=(S,A) et un sous-ensemblede sommets X, le sous-graphe de G induit (engendr´e) par X est G(X)=(X,E) o`u E={(x,y)?A|x,y?X} La d´efinition est identique dans le cas non orient´eD´efinition
Etant donn´e un graphe G=(S,A) et un sous ensemble d"arcs ou d"arˆetes E, le graphe partiel de G induit par E est le graphe G=(S,E) L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 18 / 125Exemple
Un graphe, le sous-graphe induit par X ={2,4,5,6,7} et le graphe partiel induit par l"ensemble d"arcsE={(2,2),(5,3),(4,5),(3,4),(8,7)}
graphe63 4215
7 8 sous-graphe 64257 graphe partiel
63 4215
7 8 L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 19 / 125D´efinition
Etant donn´e un graphe G=(S,A), une partition p={S1,...,Sp}de S, le graphe quotient induit par P est la graphe (V,E) o`u : V={s1,...,sp}(`a chaque partie S, on associe un sommet Si)E={(si,sj) /?(x,y)?A , x?Siet y?Sj}
Rappel
p={S1,...,Sp}est une partitionde S ssi? i= S et?i?=j,Si?Sj=∅ L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 20 / 125Exemple
Un graphe et le graphe quotient induit par la partition p={s1,...,s4} L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 21 / 125 Graphes et algorithme : pr´esentationRepr´esentationMatrice d"adjacence
Le graphe est repr´esent´e par un tableau `a deux dimensionsindex´e sur l"ensemble des sommetsGraphe et matrice d"adjacence
3 425 76 81X12345678
1FFFFFFFF
2FVFFFFFF
3FFFVVFFF
4FFFFVFFF
5FFVFVFFF
6FFFFFFVF
7FFFFFFFF
8FFFFFFVF
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 22 / 125 Les ´el´ements du tableau peuvent ˆetre diff´erents types selon le graphe consid´er´e bool´eens: un ´el´ement [i,j] est vrai si l"arc (i,j) figure dans le graphe. Dans le cas non orient´e si l"´el´ement [i,j] est vrai, alorsl"´el´ement [j,i] est vrai r´eels: Dans le cas de graphes valu´es, on repr´esente la fonction de coˆut, ainsi pour valeur c(i,j) et si l"arc (i,j) ne figure pasdans le graphe [i,j] prend une valeur conventionnelle. entiers: Dans le cas du multigraphe, [i,j] aura pˆour valeur le nombre d"arcs (i,j) figurant dans le graphe. L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 23 / 125 en C: #define N_MAX typedef struct{ int g[N_MAX][N_MAX]; int n; }grapheM; en pseudo-langage constante N_MAX = ... (* nombre maxi de sommets *) type sommet = 1..N_MAX graphe = structure a:= tableau[sommet,sommet] de booleens n: 0..N_MAX fin L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 24 / 125Avantages
Acc`es direct aux arcs : tester l"existence d"un arc, ajouter, ou supprimer un arc sont des op´erations r´ealisables en tempsconstant (θ(1)) L"´ecriture des algos est g´en´eralement simplifi´ee : l"acc`es aux successeurs d"un sommet est ais´eInconv´enients
encombrement maximal de la m´emoire : ?le nombre d"arcs figurant dans le graphe, la place m´emoire n´ecessaire est enθ(N coˆut de l"initialisation :θ(n2) coˆut de la recherche des successeurs d"un sommet :θ(n), mˆeme s"il y"a pas de successeurs. l"acc`es aux successeurs d"un sommet est ais´e L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 25 / 125Listes d"adjacence
C"est g´en´eralement la repr´esentation la plus utilis´ee, celle o`u l"on dispose des algos les plus performants.Exemple
3 425 76 81L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 26 / 125 en C: typedef struct cel{ int st; struct cel* suiv; }cellule; typedef cellule* Liste; typedef struct{
Liste a[N_MAX];
int n; }grapheL; L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 27 / 125 en pseudo-langage: type Liste = ^cellule cellule = structure st : sommet suiv : Liste fin grapheL = structure a := tableau [sommet,sommet] de Liste n :0..N_MAX fin L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 28 / 125Avantages
encombrement minimal de la m´emoire :θ(NMAX+m) l"acc`es au successeur d"un sommet x est enθ(d+(x))Inconv´enients
cout d"acc`es `a un arc l"origine x :θ(d+(x)) l"acc`es aux pr´ed´ecesseurs d"un sommet x impose le parcours de toutes les listes d"adjacence :θ(n+m) L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 29 / 1251Graphe et algorithme : pr´esentation
2Parcours, num´erotation et descendance
3Connexit´e et forte connexit´e
4Graphes sans circuit
5Probl`eme du plus court chemin
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 30 / 125D´efinition (Graphe orient´e)
un chemin x i1,xi2,...,xiksera not´e [xi1,xi2,...,xik] un chemin [xi1,xi2,...,xik] est dit ´el´ementairesi (ne contient pas deux fois le mˆeme sommet) la longueur d"un cheminest ´egale au nombre de sommets moins un. le chemin constitu´e du seul sommet x i1not´e [xi1] est de longueur nulle.Propri´et´e
si c=[xi1,...,xik] est un chemin de G, alors il existe une sous-suite de c qui est un chemin ´el´ementaire de x i1`a xik. xi1 xij xij+1 xil xik L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 31 / 125Preuve :Par r´ecurrence sur r
, le nombre de r´ep´etitions de sommets dans c. si r=0, c"est un chemin ´el´ementaire Supposons que la propri´et´e est vraie au rang r-1 Soit un chemin c=[xi1,...,xik] poss´edantr r´ep´etitions. Soit c" la sous-s´equence de c obtenue en supprimant de c la sous-suite x iu+1... xiv.Donc c"=[x
i1,...,xiu,xiv+1,...,xik] est un chemin ayant au plus c-1 r´ep´etitions, d"o`u par hypoth`ese de r´ecurrence c" qui est une sous-s´equence de c pos`ede une sous-s´equence qui est un chemin´el´ementaire de x
i1`a xik: c=[x i1,...,(xiu,...,xiv),xiv+1,...,xik] L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 32 / 125D´efinitions (Graphe non orient´e)
une chaˆınede G=(S,A) est une s´equence de sommets x (x ij,xij+1)?A ou (xij+1,xij)?A une chaˆıne(xi1,...,xik) est dite ´el´ementairesi (ne contient pas deux fois le meme sommet) la longueur d"une chaineest ´egale au nombre de sommets moins un.La chaine constitu´ee du seul sommet x
i1sera not´ee (xi1) est de longueur nulle.D´efinition
un circuit de G=(S,A) est un chemin [xi1,...,xik] de G tel que?k≥2 et xi1=xik. un cycle de G=(S,A) est une chaine (xi1,...,xik) de G tel que?k≥2 et xi1=xik. L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 33 / 125D´efinition
Etant donn´e un graphe G=(S,A) et x?S, on d´efinit les ensembles de descendants et ascendants d"un sommet x: descG(x)={y?S| ?[x,y] dans G} ascG(x)={y?S| ?[y,x] dans G} =>?x,y?S, y?descG(x)<=>x?ascG(y)Propri´et´e
Soit G=(S,A) un graphe
?x?S, ascG(x)=descG-1(x)D´efinition
Une racinede G=(S,A) est un sommet r de S tel que S=descG(r) L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 34 / 125Parcoursenprofondeur :
Exemple
Parcours en profondeur d"un graphe : les num´eros correspondants aux sommets donnant l"ordre dans lequel les sommets sont visit´es. L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 35 / 125 algorithme: procedure parcoursProfondeur(g : graphe); variable atteint : tableau[sommet] de booleens (atteint[x] <=> le sommet x a ete atteint) x : sommet debut pour tout sommet x de g faire atteint[x]:=faux pour tout sommet x de g faire si non atteint[x] alors RechercheProf(x) fin L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 36 / 125 procedure RechercheProf(x : sommet);{specifications : etant donnee un sommet x non atteint, cette procedure marque x, et tous les sommets y descendants de x tels qu"il existe un chemin [x,y] dont aucun sommet n"est marque} variable y : sommet debut atteint[x]:=vrai pour tout successeur y de x faire si non atteint[y] alors RechercheProf(y) fin L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 37 / 125Complexit´e:
La phase d"initialisation du tableau atteint est enθ(n). L"it´eration de l"algorithme principal est r´ealis´e exactement en n ´etapes, pour chacune il y"a au moins un test r´ealis´e. θ(n+m), soitθ(max(n,m)) dans le cas des listes d"adjacences.θ(n2) dans le cas des matrices d"adjacence.
L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 38 / 125 Ordredetraitement-Num´erotation : (parcours en profondeur) L"objet des parcours de graphes concerne des traitements que l"on souhaite op´erer sur les graphes. Les traitements s"op`erent parfois sur les sommets visit´es. Il est alors possible d"op´erer un traitement avant ou apr`es la visite du sommet. Il y"a donc soit un traitement en pr´eOrdre ou ordre pr´efix´e, soit en postOrdre ou ordre postfix´e. Ceci se traduit par une modification de la proc´edure de recherche en profondeur. traitementenpr´eOrdre var y : sommet debut atteint[x]:=vraiExemple
num´erotation en pr´e-ordre(rouge) et en post-ordre(vert) pour un parcours en profondeur L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 40 / 125Mise en oeuvre en C du parcours en profondeur:
typedef struct cel{ int st; struct cel* suiv; }cellule typedef cellule* Liste; typedef struct{Liste a[N_MAX];
int n; }grapheL; typedef int atteint[N_MAX]; /* variables globales d´eclar´ees: grapheL g; atteint m: */ L. Sais (Algorithmique & Programmation 5)Th´eorie des graphes7 avril 2011 41 / 125quotesdbs_dbs44.pdfusesText_44[PDF] de l'année 1789 ? l'exécution du roi cm1
[PDF] graphe d'ordonnancement
[PDF] sujet algorithme bts sio corrigé
[PDF] calcul matrice booléenne
[PDF] calcul matriciel bts
[PDF] prise de note rapide tableau abréviations
[PDF] sauzay programme
[PDF] programme voltaire
[PDF] un petit paragraphe sur l'environnement
[PDF] exemple de texte argumentatif sur l'environnement
[PDF] texte sur l'environnement
[PDF] texte argumentatif sur l'environnement 4am
[PDF] protection de l'environnement définition
[PDF] graphe probabiliste calculatrice
