 Validation et optimisation dune décomposition hiérarchique de
Validation et optimisation dune décomposition hiérarchique de
24 janv. 2012 Dans ce cadre une généralisation de cette mesure de qualité au cas multi-niveaux est introduite. Nous testons notre méthode sur des graphes ...
 Théorie des graphes
Théorie des graphes
7 avr. 2011 Théorie des graphes. 7 avril 2011. 75 / 125. Page 76. Graphes sans circuit. S-séquence d'un graphe - Décomposition par niveaux. Définition. Soit ...
 CHAPITRE 2 : Théorie des graphes et applications
CHAPITRE 2 : Théorie des graphes et applications
une marque `a chaque sommet du graphe ordonné en niveaux. a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur
 Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
graphe niveau par niveau à partir d'un sommet donné ;. – le parcours en ... Un projet est généralement décomposé en différentes tâches à effectuer. Chaque ...
 GRAPHES
GRAPHES
2 avr. 2008 Graphes sans circuit. Lorsque le graphe est sans circuit il peut être décomposé en niveaux. La longueur du chemin de la racine `a tous les ...
 Décomposition algorithmique des graphes
Décomposition algorithmique des graphes
23 mai 2007 composition en branches d'un hyper-graphe planaire une décomposition de ... au niveau de ses extrémités et uniquement à cet endroit. Comme une ...
 Étude dalgorithmes de décomposition de graphes
Étude dalgorithmes de décomposition de graphes
1 sept. 2020 Il nous faut aussi définir la famille des graphes chordaux car ils sont étroitement liés aux tree-decompositions. Étant donné un graphe G un ...
 Théorie des graphes DUT Informatique semestre 2
Théorie des graphes DUT Informatique semestre 2
3 févr. 2014 courts dans un graphe il faut donc savoir décomposer un graphe en niveaux. È2.8 Décomposition en niveau d'un graphe sans circuit : 1. 2. 3. 4.
 Chapitre 6 Décompositions arborescentes†
Chapitre 6 Décompositions arborescentes†
sans arêtes communes et ces sous-graphes sont « recollés » au niveau de leurs Nous venons de définir un opérateur de décomposition d'un graphe en deux sous- ...
 Les plans dexpériences par la méthode TAGUCHI
Les plans dexpériences par la méthode TAGUCHI
niveaux décomposé en nombre premier (l'interaction BC à 6 niveaux a été Pour construire 2 colonnes à 4 niveaux il faut partir d'un graphe linéaire.
 Théorie des graphes
Théorie des graphes
7 avr. 2011 S-séquence d'un graphe - Décomposition par niveaux. 5 Probl`eme du plus court chemin. L. Sais (Algorithmique & Programmation 5).
 Corrigé TD1 13-14
Corrigé TD1 13-14
À partir de ces listes on obtient la décomposition par niveaux : S0 = {E H}
 CHAPITRE 2 : Théorie des graphes et applications
CHAPITRE 2 : Théorie des graphes et applications
a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur maximale au sens des arcs allant de.
 Table des matières
Table des matières
2 Décomposition des graphes Décomposition basée sur la matrice de la fermeture transitive ... décomposition d'un graphe sans circuit en niveaux.
 Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
le parcours en largeur consiste à explorer les sommets du graphe niveau par Un projet est généralement décomposé en différentes tâches à effectuer.
 Théorie des graphes DUT Informatique semestre 2
Théorie des graphes DUT Informatique semestre 2
3 fév. 2014 Pour décomposer en niveau un graphe G on utilisera l'algorithme suivant : ... il faut donc savoir décomposer un graphe en niveaux.
 Quelques propriétés des graphes distances héréditaires
Quelques propriétés des graphes distances héréditaires
6.3.1 Rappels sur la décomposition par substitution . . . . . 26. 6.3.2 Pour les graphes 2 – Un exemple de graphe avec les niveaux de distances.
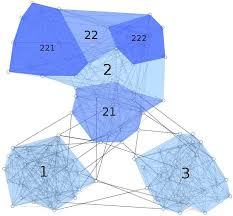
 Structure multi-échelle de grands graphes de terrain
Structure multi-échelle de grands graphes de terrain
Graphe avec représentation de la décomposition niveau par niveau et de l'arbre obtenu. Les feuilles de l'arbre sont les sommets du graphe initial.
 Méthodes dOptimisation
Méthodes dOptimisation
1.1.2 Niveaux des sommets d'un graphe sans circuit . Le mouvement de mati`ere se décompose en un nombre fini de mouvements partiels chacun allant d'un.
 PLANIFICATION et Ordonnancement
PLANIFICATION et Ordonnancement
Les rangs (ou niveaux) déterminés permettent de positionner le début des différentes tâches lors de la construction du graphe.
 IT3004 Graphes et algorithmes Notes de cours et exercices - ESIEE
IT3004 Graphes et algorithmes Notes de cours et exercices - ESIEE
Exemple 1 : Soit un graphe G=(E?) avec E ={1234}et ? dé?nie par : ?(1)={124} ?(2)={31} ?(3)={4} ?(4)=0/ Iln’estpasfaciledevisualiserungraphedonnésouscetteforme Habituellementonreprésente ungrapheparundessintelqueceluidela?gure1 1pagesuivante Notonsqueplusieursdessins comme pour cet exemple peuvent représenter le même
 Les graphes - univ-reunionfr
Les graphes - univ-reunionfr
De manière générale un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication réseaux routiers interaction de diverses espèces animales circuits électriques )
 Théorie des graphes et optimisation dans les graphes - CNRS
Théorie des graphes et optimisation dans les graphes - CNRS
i(dans le cas d’un 1-graphe on aura d +(s i) =jsucc(s i) j) De même le demi-degré intérieur d’un sommet s i noté d (s i) est le nombre d’arcs arrivant à s i(dans le cas d’un 1-graphe on aura d (s i) =jpred(s i) j) Exercice : Dessiner un graphe non orienté complet à 4 sommets Quel est le degré des som-mets de ce graphe?
 Chapitre 3 - Graphes 1 Graphes et modes de représentation
Chapitre 3 - Graphes 1 Graphes et modes de représentation
Pour le rendre plus lisible il est souvent utile de représenter un graphe par niveaux Pour cela il faut déterminer le niveau de chacun des sommets du graphe Proposition Le niveau d'un sommet a autv : 0 si a n'a pas de prédécesseur 1+nmax sinon où nmax est le maximum des niveaux des prédécesseurs de a Méthode
 Searches related to décomposition d+un graphe en niveaux PDF
Searches related to décomposition d+un graphe en niveaux PDF
La treelength d’un graphe est elle aussi toujours dé?nie : la length de la décomposition constituée d’un seul sac contenant tous les sommets du grapheestégaleaudiamètredugraphe(ladistanceentrelesdeuxsommets lespluséloignés)unebornesupérieuredelatreelength Figure 5–Ungrapheetunetree-decompositiondecegraphe
Quel est le degré d’un graphe?
3.b Ordre et degré On appelleordred’un graphe le nombre de ses sommets. Ledegréd’un sommet est le nombre d’arrêtes dont il est une extrémité. Deux sommets reliés par une même arrête sont ditsadjacents.
Quel est le degré d’un graphe d’ordre 4?
b D Ce graphe comporte 4 sommets, c’est donc un graphe d’ordre 4. • Du sommet A partent 4 arrêtes. Le degré du sommet A est donc 4. • Le degré du sommet B est 3. • Le degré du sommet C est 4. • Le degré du sommet D est 1.
Quels sont les problèmes des graphes pondérés?
J 10 25 97 12 30 39 17 L’un des problèmes classiques des graphes pondérés est celui de recherche d’un trajet routier le plus court (en terme de temps ou de kilomètres). Si un graphe n’est pas pondéré, le poids de chaque arête peut être considéré comme égale à 1.
Quel est le rôle d'un graphe?
De manière générale, un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication, réseaux routiers, interaction de diverses espèces animales, circuits électriques...)
Th´eorie des graphes
DUT Informatique, semestre 2
Version 2.0
3 f´evrier 2014
Ph. Roux
2009-2014
2Table des mati`eresTable des mati`eres3
Origines historiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 Diff´erentes notions de graphes . . . . . . . . . . . . . . . . . . . . . . 7
1.1 Relations binaires . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2 Relation dans un ensemble . . . . . . . . . . . . . . . . . . . . 16
1.3 Graphes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.4 Autres types de graphes . . . . . . . . . . . . . . . . . . . . . 23
1.5 Quelques probl`emes courants de th´eorie des graphes . . . . .30
2 Chemins dans un graphe . . . . . . . . . . . . . . . . . . . . . . . . . 35
2.1 D´efinitions et premiers exemples . . . . . . . . . . . . . . . . . 35
2.2 graphes Euleriens et Hamiltoniens . . . . . . . . . . . . . . . . 37
2.3 Parcours de graphes orient´es . . . . . . . . . . . . . . . . . . . 46
3 Probl`emes d"optimisation pour des graphes valu´es . . . . . . . . . .. 54
3.1 Arbre couvrant optimal . . . . . . . . . . . . . . . . . . . . . 54
3.2 Probl`eme du plus court chemin . . . . . . . . . . . . . . . . . 56
3.3 Ordonnancement et gestion de projet . . . . . . . . . . . . . . 64
3.4 Flots dans les r´eseaux . . . . . . . . . . . . . . . . . . . . . . 70
4 Notions de th´eorie des langages . . . . . . . . . . . . . . . . . . . . . 81
4.1 Alphabets, langages et grammaires formelles . . . . . . . . . . 81
4.2 Langages r´eguliers et automates Finis . . . . . . . . . . . . . . 86
4.3 Langages alg´ebriques . . . . . . . . . . . . . . . . . . . . . . . 98
5 Metanet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
5.1 L"´editeur de graphes metanet . . . . . . . . . . . . . . . . . . 100
5.2 Chargement d"un graphe dansScicoslab. . . . . . . . . . . . 104
5.3 Variable de typegraphdansScicoslab. . . . . . . . . . . . . 106
5.4 Quelques fonctions pour les graphes . . . . . . . . . . . . . . . 112
5.5 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
Bibliographie120
Liste des Exercices121
3Avertissement
Pour bien utiliser ce polycopi´e, il faut le lire au fur et `a mesure de l"avancement du cours magistral, et prendre le temps de refaire les exercices types qui y sont propos´es. Les d´efinitions et th´eor`emes sont num´erot´es suivant le mˆeme ordre que dans le cours magistral. Th´eor`eme 0.0.0les th´eor`emes apparaissent toujours dans un cadre gris´e commecelui-ci et sont en g´en´eral suivis de leur d´emonstration, signal´ee par une barre dans
la marge et un?`a la fin comme ci-dessous :Preuve :D´ebut de la d´emonstration ...
...fin de la d´emonstration ?La table des mati`eres et l"index (`a la fin du document) permettentde retrou- ver une notion pr´ecise dans ce polycopi´e. Les m´ethodes et techniques qui seront approfondies en TD sontsignal´ees par un cadre (sans couleurs) Des exercices types corrig´es,r´edig´es comme vous devriez le faire enDS, sont signal´es par le symbole : Les erreurs et les confusions les plus fr´equentes sont signal´ees dans des cadres rouges avec le symbole : Vous ˆetes libre de r´eutiliser le contenu de ce document sous les termes de la licence CC-BY-NC-SA [11] 4 DUT InformatiqueTh´eorie des graphesMath´ematiquesOrigines historiques Les math´ematiques fournissent de puissants outils pour mod´eliser des probl`emes de toutes sortes : les structures bool´eennes pour les probl`emes de logique (?,?,¬, =?, ...) les ensembles pour repr´esenter des collections d"objetsN,R,R2,Mp,n(R) ... les fonctions, d´eriv´ees, int´egrales pour r´ealiser des calculs ... Mais ses outils sont insuffisants, mˆeme `a notre niveau, pour pouvoir mod´eliser des probl`emes d"apparence pourtant assez simple. Un bon exemple de ce type de probl`eme peut ˆetre trouv´e dans le domaine des bases de donn´ees : comment mod´eliser les liens entre des objets pris dans diff´erents ensembles?? Pour cela nous avons besoin d"un nouveau type d"objet math´ematiques :les graphes. Par rapport aux autres th´eories math´ematiques ´etudi´ees `a l"IUT, la th´eorie des graphes est assez r´ecente. L"article consid´er´e comme fondateur de la th´eorie des graphes fut pr´esent´e par le math´ematicien suisse Leonhard Euler `a l"Acad´emie de Saint P´etersbourg en 1735, puis publi´e en 1741, et traitait du probl`eme des sept ponts de K¨onigsberg. Le probl`eme consistait `a trouver une promenade `a partir d"un point donn´e qui fasse revenir `a ce point en passant une fois et une seule par chacun des sept ponts de la ville de K¨onigsberg. Au milieu duXIXi`eme, c"est le?th´eor`eme des quatre couleurs?qui va po- pulariser dans le monde des math´ematiques cette th´eorie peu connue jusque l`a. Ce th´eor`eme affirme qu"on a besoin que de quatre couleurs diff´erentes pour colo- rier n"importe quelle carte g´eographique de telle sorte que deux r´egions limitrophes (ayant toute une fronti`ere commune) re¸coivent toujours deux couleurs distinctes. Le r´esultat fut conjectur´e en 1852 par Francis Guthrie, int´eress´e par la coloration de la carte des r´egions d"Angleterre, mais ne fˆut d´emontr´e qu"en 1976 par deux Am´ericains Kenneth Appel et Wolfgang Haken. Leur d´emonstration de ce th´eor`eme fut la premi`ere `a utiliser un ordinateur pour ´etudier les 1478 casparticulier aux quels se ram`ene le probl`eme des quatre couleurs critiques ce quin´ecessita plus de1200 heures de calcul!
C"est donc auXXi`emeque cette th´eorie va connaˆıtre son v´eritable essor avec l"utilisation croissante dans la vie quotidienne des r´eseaux dont il faut optimiser l"utilisation constamment : r´eseaux de transport routier, transport d"eau, d"´electricit´e r´eseaux de transport de donn´ees (r´eseau de t´el´ephonie fixe, GSM, wifi ...) r´eseaux d"informations (bases de donn´ees, web, r´eseaux sociaux ...) Cette th´eorie est devenue fondamentale en informatique car elle fournit de nombreux algorithmes pour r´esoudre des probl`emes complexes repr´esent´es par des graphes de tr`es grande taille (plusieurs centaines, milliers,... de sommets et d"arcs!). 5 DUT InformatiqueTh´eorie des graphesMath´ematiquesFigure1 - les 7 ponts de K¨onigsberg
Figure2 - une carte g´eographique colori´ee avec 4 couleurs seulement 6DUT InformatiqueTh´eorie des graphesMath´ematiques1 Diff´erentes notions de graphes1.1 Relations binaires
La notion de graphe repose avant tout sur la notion derelation binaire, pour l"introduire nous allons commencer par prendre un exemple de la vie courante.?1.1 Emploi du tempsUn emploi du temps met en relation des jours (ou des
cr´eneaux horaires) et des mati`eres (et ´eventuellement des enseignants, des salles ...) :Lundi MardiMercredi
JeudiVendredi
Samedi
Dimanche
ArchiSyst`eme
Algo Maths EGO AlgoSyst`eme
Anglais
EC EGO Archi Archi Algo Algo Maths Algo EC Maths On est donc en pr´esence de deux ensembles de donn´ees dans cet exemple : les jours de la semaine et Les mati`eres enseign´ees. Mais il y a une donn´ee suppl´ementaire qu"on ne peut pas repr´esenter par un ensemble : la relation qui existe entre les jours et les mati`eres. On peux l"exprimer simplement par la phrase : une mati`ere est en relation avec les jours de la semaine o`u elle est enseign´ee? On peut essayer de repr´esenter ces liens sur un diagramme enles repr´esentant par des fl`eches comme sur la figure FIG.3. On se rend alors facilement compte qu"on ne peut pas mod´eliser ces liens en utilisant des fonctions ou des applications d"un des ensembles vers l"autre. On a besoin d"une notion plus g´en´erale ... Sport Archi AlgoSyst`eme
Anglais
EC EGOMathsLundi
MardiMercredi
JeudiV endredi
Samedi
Dimanche
Mati`eresRJours
Figure3 - Relations entre les mati`eres et les o`u elles sont enseign´ees 7DUT InformatiqueTh´eorie des graphesMath´ematiquesD´efinition 1.1 (Relation binaire)SoientEetFdeux ensembles alors
?Rest une relation deEversF?siRest la donn´ee d"un triplet d"ensembles (E,F,U)tel queU?E×F. On dit que?xest en relation avecy?si et seulement si(x,y)?Uce qui sera not´exRy Au contraire si?xn"est pas en relation avecy?on ´ecrirax?Ry On repr´esentera une relationR= (E,F,U)par un diagramme sagittal (ou diagramme fl´ech´e) pour cela : - on dessine les diagrammes de Venn des ensemblesEetF - chaque couple(x,y)?Uest repr´esent´e par une fl`eche allant dex`ay Pour des raisons pratiques on utilisera le vocabulaire suivant pour d´esigner lesdiff´erents ensembles associ´ees `a la d´efinition de relation binaire:D´efinition 1.2 (Lexique de la th´eorie des graphes)Pour une relationR, d´efinie par le triplet(E,F,U), telle quexRyon dira :
Eest l"ensemble de d´epart,Fcelui d"arriv´e etUcelui des arcs. xest le pr´ed´ecesseur dey, on dit aussi l"origine de(x,y) l"ensemble des pr´ed´ecesseurs deyestΓ-(y) d-(y) = CardΓ-(y)est le degr´e entrant enyle domaine deR:DR={x?E| ?y?F,(x,y)?U}
yest le successeur dex, on dit aussi l"extr´emit´e de(x,y)l"ensemble des successeurs dexestΓ+(x)
d+(x) = CardΓ+(x)est le degr´e sortant dexl"image deR:ImR={y?F| ?x?E,(x,y)?U}
Il est tr`es facile de retenir le sens de certaines de ces notions en pensant `a la repr´esentation graphique de la relation par un diagramme sagittal(ensembles de d´epart et d"arriv´e, successeurs, pr´ed´ecesseur) Mais d"autres sont moins faciles `a retenir (domaine, image, degr´e). Il faut donc bien retenir ces d´efinitions d`es main- tenant.?1.2 Exprimer ces diff´erents ensembles pour la relation de laFIG.3
D´epart :E={Sport;Archi;Algo;...;Maths}
Arriv´ee :F={Lundi;Mardi;Mercredi;...;Dimanche} Arcs :U={(Archi,Lundi);(Archi,Mardi);...;(Maths,V endredi)}Domaine :DR=E\ {sport}
Image :ImR=F\ {Samedi;Dimanche}
Γ+(Maths) ={Jeudi;V endredi}=?d+(Maths) = 2Γ-(Jeudi) ={Maths;EC;Algo}=?d-(Jeudi) = 3
8 DUT InformatiqueTh´eorie des graphesMath´ematiques On peut aussi rapprocher ce vocabulaire du vocabulaire utilis´es pour les fonctions et applications qui sont en fait des cas particuliers de relations!1.3 Cas des fonctions et applicationsreprendre les d´efinitions du cours de
th´eorie des ensembles concernant les fonctions et applications du point de vue des relations binaires :Fonctionsune fonctionf:E-→Fest une relation
xRy??f(x) =y R´eciproquement, une relationRest une fonction si chaque ´el´ement deE`a au plus un successeur ApplicationsUne relationR:E-→Fest une application si et seulement si :Rest une fonction
Son domaine de d´efinition est ´egal `aE ce qui s"exprime en langage des relations binaires par ?x?E,Card(Γ+(x)) = 1?? ?x?E, d+(x) = 1 Application injective surjective, bijectiveSoitf:E-→Fune application, on dit quefest injective si chaque ´el´ement deF`a au plus un pr´ed´ecesseur surjective si chaque ´el´ement deF`a au moins un pr´ed´ecesseur ?y?F,Card(Γ-(y))≥1?? ?y?F, d-(y)≥1bijective si elle est injective et surjective
?y?F,Card(Γ-(y)) = 1?? ?y?F, d-(y) = 1 ?Ces d´efinitions ont une grande importance en base de donn´ees, elles sont direc- tement li´ees aux cardinalit´es qui apparaissent dans un MCD. Ellespermettentd"expliquer pourquoi :Une relation fonctionnelle qui apparaˆıt dans un MCD n"aura pas de table
propre Une relation bijective ne devrait jamais apparaˆıtre dans un MCD 9 DUT InformatiqueTh´eorie des graphesMath´ematiques?1.4 Reconnaˆıtre `a partir des diagramme sagittaux les d´efinitions
pr´ec´edentes : reconnaˆıtre les fonctions et les applications des autres relations: 1 2 3 4a b c d eEhF 1 2 3 4 5a b c d eEg F 1 2 3 4 5a b c dEfFgetfsont des fonctions
fest une application mais pasg(card+(5) = 0ou encoreDg=E\{5} ?= E) ethn"est pas une fonction (card+(5) = 2) donc pas une application reconnaˆıtre injectivit´e, surjectivit´e et bijectivit´e: 1 2 3 4a b c d eEf 1F 1 2 3 4 5a b c dEf 2F 1 2 3 4 5a b c d eEf 3F ce sont bien des applications et : f1est injective mais pas surjective (`a cause ded-(e) = 0) f2est surjective mais pas injective (`a cause ded-(d) = 2)seulef3est bijective
On retrouve sur ces exemples les r´esultats du th´eor`eme suivant :Th´eor`eme 1.3
SoientE,Fdes ensembles finis etf:E-→Fune application alorssifest surjective alorsCard(E)≥Card(F)
sifest bijective alorsCard(E) = Card(F)
10 DUT InformatiqueTh´eorie des graphesMath´ematiques Le diagramme sagittal permet de d´etecter de nombreuses propri´et´es d"une re- lation binaire, `a condition qu"il n"y ait pas trop d"arc ni d"´el´ements. Pour pou- voir analyser les propri´et´es de graphes de grandes tailles nous avons besoin d"une repr´esentation qui permette de faire des calculs : une matrice.D´efinition 1.4 (matrice d"adjacence)
SoientE={x1;x2;...;xp},F={y1;y2;...;yn}etR= (E,F,U)une relation alors on appelle matrice d"adjacence deRla matrice bool´eenneMR?Mp,n(B)telle que MR= (mi,j)avecmi,j=?1si(xi,yj)?U
0sinon?Pour pouvoir ´ecrire la matrice d"adjacence d"une relation il faut avoir choisi
un ordre pour les ´el´ements des ensemblesEetF(il sont num´erot´esx1,x2,... pourEety1,y2,...pourF). Ce choix est arbitraire, mais il n"est pas indiqu´e dans la matrice d"adjacence!On prendra donc (sauf mention contraire) l"ordre lexicographique pour ordonner les ´el´ements deEetF.Une fois qu"on a ordonn´e les ´el´ements des ensemblesEetFchaque relation est repr´esent´ee par une matrice et chaque matrice repr´esente une relation?1.5 Repr´esentation d"une relation `a l"aide d"une Matriced"adjacence
Comme il n"y a pas `a priori d"ordre sur les ´el´ements d"un ensemble il faut souvent faire attention pour remplir la matrice d"adjacence `a partir d"un diagramme sagittal o`u les ´el´ements ne sont pas forc´ement class´e dans l"ordre lexicographique1. Ici on choisit l"ordre lexicographique pour l"ensemble des mati`eres mais pas pour l"ensemble des jours (o`u il y a un ordre plus naturel) ce qui donne : Sport Archi AlgoSyst`eme
Anglais
EC EGOMathsLundi
MardiMercredi
JeudiV endredi
Samedi
Dimanche
Mati`eresR
Jours-→((((((((((((((1 0 1 1 0 0 00 0 1 0 0 0 01 1 0 0 0 0 01 0 1 1 0 0 00 0 0 1 0 0 00 0 0 0 1 0 00 0 0 1 1 0 00 0 0 0 0 0 00 1 0 0 0 0 0))))))))))))))
Pour mieux comprendre la matrice d"adjacence on peut y faireapparaˆıtre les´el´ements des ensemblesEetF
1. ¸ca ne donnerait pas forc´ement un diagramme tr`es lisible
11 DUT InformatiqueTh´eorie des graphesMath´ematiques (lundi mardi mercredi jeudi vendredi samedi dimancheAlgo1 0 1 1 0 0 0
Anglais0 0 1 0 0 0 0
Archi1 1 0 0 0 0 0
Algo1 0 1 1 0 0 0
EC0 0 0 1 0 0 0
EGO0 0 0 0 1 0 0
Maths0 0 0 1 1 0 0
Sport0 0 0 0 0 0 0
Syst`eme0 1 0 0 0 0 0))))))))))))))
?On se rappellera que dans la matrice d"adjacence : leslignescorrespondent aux ´el´ements de l"ensemble de d´epart lescolonnescorrespondent aux ´el´ements de l"ensemble de arriv´eeLe d´efaut de la matrice d"adja-
cence est quelle contient beaucoup de0. D"un point de vue informatique
cela repr´esente un gaspillage de place m´emoire. C"est pourquoi on repr´esente parfois ces matrices sous forme de ?ma- trice creuse ?, c"est `a dire en donnant seulement la position de chaque coeffi- cient non-nul de la matrice (ainsi que sa taille). C"est la repr´esentation qui est uti- lis´ee en base de donn´ees pour repr´esenter la table associ´ee `a un TA. Dans le cas de la relation repr´esent´ee FIG.3 la matrice d"adjacence sera repr´esent´ee comme ci- contre : i j mij 1 1 1 1 3 1 1 4 1 2 3 1 3 1 1 3 2 1 4 1 1 4 3 1 4 4 1 5 4 1 6 5 1 7 4 1 7 5 1 9 2 1 La matrice d"adjacence permet de faire de nombreux calculs, commepar exemples compte le nombre de relations entre deux ensembles. Th´eor`eme 1.5 (Nombres de relations entre 2 ensembles) SiEetFsont des ensembles finis alors le nombre de relations deEversFest 2Card(E×F)= 2Card(E)×Card(F)
Preuve :Il suffit de compter le nombre de Matrices d"adjacences : la matrice d"adjacence est de taille Card(E)×Card(F) Chaque case peut ˆetre remplie de 2 mani`eres 0 ou 1 On a donc au total 2×2× ··· ×2?Card(E)×Card(F) r´ep´etitions= 2
Card(E)×Card(F)possibilit´es
Mais surtout la matrice d"adjacence permet de calculer de nouvelles relations `a partir de relations connues. Commen¸cons par la composition des relations. 12DUT InformatiqueTh´eorie des graphesMath´ematiquesD´efinition 1.6 (Composition de relations)SoientR1= (E,F,U1)etR2=
(F,G,U2)2 relations alors on appelleT=R2◦R1= (E,G,U)la relation dont les arcs sont :U={(x,z)?E×G| ?y?F,(x,y)?U1et(y,z)?U2}?
1.6 composition de deux relationsT=R2◦R1il y a un arc joignant
un ´el´ement deEet un ´el´ement deGdans le diagramme de la relationTsi on trouve dans les diagrammes deR1etR2un chemin entre ces ´el´ements passant par un ´el´ement deF: 1 2 3 4 5a b c d eER 1F a b c d eαεFR
2G 1 2 3 4 5αεETG
Figure4 - Composition de relations
La composition de deux relations correspond au produit matriciel des matrices d"ad- jacence.Th´eor`eme 1.7
SiE,F,Gsont des ensembles finis alors la matrice d"adjacence deT=R2◦R1est donn´ee par le produit matriciel suivant : MT=MR2◦R1=MR1×MR2
Ce produit matriciel est effectu´e avec les op´erations de l"alg`ebre de Boole binaire!Preuve :On note
On peut d´ej`a remarquer que la relation compos´eeTva deEversGT=R2◦R1:ER1-→FR2-→G
donc sa matrice doitˆetre de taillep×nce qui correspond bien `a la taille du r´esultat du produit matricielMR1×MR2. Ensuite en reprenant la formule du produit matriciel : MT(i,j) =l?
k=1MR1(i,k)×MR2(k,l)
13DUT InformatiqueTh´eorie des graphesMath´ematiquesla somme et le produit sont faits dans l"alg`ebre de Boole binaireBdonc il suffit
qu"un seul des termes du produit soit non-nul (´egal `a 1) pour queMT(i,j) = 1 cela veut dire qu"il existektel queMR1(i,k) = 1 etMR2(k,l) = 1. Cela revient `a dire qu"il existe un arcs (xi,yk) dansR1et un autre (yk,zj) dansR2, il y a donc bien un arc (xi,zj) dansT??Attention `a l"ordre des termes dans le produit matriciel, la matrice d"adjacencequotesdbs_dbs44.pdfusesText_44[PDF] de l'année 1789 ? l'exécution du roi cm1
[PDF] graphe d'ordonnancement
[PDF] sujet algorithme bts sio corrigé
[PDF] calcul matrice booléenne
[PDF] calcul matriciel bts
[PDF] prise de note rapide tableau abréviations
[PDF] sauzay programme
[PDF] programme voltaire
[PDF] un petit paragraphe sur l'environnement
[PDF] exemple de texte argumentatif sur l'environnement
[PDF] texte sur l'environnement
[PDF] texte argumentatif sur l'environnement 4am
[PDF] protection de l'environnement définition
[PDF] graphe probabiliste calculatrice
