 Validation et optimisation dune décomposition hiérarchique de
Validation et optimisation dune décomposition hiérarchique de
24 janv. 2012 Dans ce cadre une généralisation de cette mesure de qualité au cas multi-niveaux est introduite. Nous testons notre méthode sur des graphes ...
 Théorie des graphes
Théorie des graphes
7 avr. 2011 Théorie des graphes. 7 avril 2011. 75 / 125. Page 76. Graphes sans circuit. S-séquence d'un graphe - Décomposition par niveaux. Définition. Soit ...
 CHAPITRE 2 : Théorie des graphes et applications
CHAPITRE 2 : Théorie des graphes et applications
une marque `a chaque sommet du graphe ordonné en niveaux. a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur
 Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
graphe niveau par niveau à partir d'un sommet donné ;. – le parcours en ... Un projet est généralement décomposé en différentes tâches à effectuer. Chaque ...
 GRAPHES
GRAPHES
2 avr. 2008 Graphes sans circuit. Lorsque le graphe est sans circuit il peut être décomposé en niveaux. La longueur du chemin de la racine `a tous les ...
 Décomposition algorithmique des graphes
Décomposition algorithmique des graphes
23 mai 2007 composition en branches d'un hyper-graphe planaire une décomposition de ... au niveau de ses extrémités et uniquement à cet endroit. Comme une ...
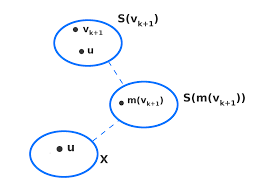 Étude dalgorithmes de décomposition de graphes
Étude dalgorithmes de décomposition de graphes
1 sept. 2020 Il nous faut aussi définir la famille des graphes chordaux car ils sont étroitement liés aux tree-decompositions. Étant donné un graphe G un ...
 Théorie des graphes DUT Informatique semestre 2
Théorie des graphes DUT Informatique semestre 2
3 févr. 2014 courts dans un graphe il faut donc savoir décomposer un graphe en niveaux. È2.8 Décomposition en niveau d'un graphe sans circuit : 1. 2. 3. 4.
 Chapitre 6 Décompositions arborescentes†
Chapitre 6 Décompositions arborescentes†
sans arêtes communes et ces sous-graphes sont « recollés » au niveau de leurs Nous venons de définir un opérateur de décomposition d'un graphe en deux sous- ...
 Les plans dexpériences par la méthode TAGUCHI
Les plans dexpériences par la méthode TAGUCHI
niveaux décomposé en nombre premier (l'interaction BC à 6 niveaux a été Pour construire 2 colonnes à 4 niveaux il faut partir d'un graphe linéaire.
 Théorie des graphes
Théorie des graphes
7 avr. 2011 S-séquence d'un graphe - Décomposition par niveaux. 5 Probl`eme du plus court chemin. L. Sais (Algorithmique & Programmation 5).
 Corrigé TD1 13-14
Corrigé TD1 13-14
À partir de ces listes on obtient la décomposition par niveaux : S0 = {E H}
 CHAPITRE 2 : Théorie des graphes et applications
CHAPITRE 2 : Théorie des graphes et applications
a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur maximale au sens des arcs allant de.
 Table des matières
Table des matières
2 Décomposition des graphes Décomposition basée sur la matrice de la fermeture transitive ... décomposition d'un graphe sans circuit en niveaux.
 Théorie des graphes et optimisation dans les graphes Table des
Théorie des graphes et optimisation dans les graphes Table des
le parcours en largeur consiste à explorer les sommets du graphe niveau par Un projet est généralement décomposé en différentes tâches à effectuer.
 Théorie des graphes DUT Informatique semestre 2
Théorie des graphes DUT Informatique semestre 2
3 fév. 2014 Pour décomposer en niveau un graphe G on utilisera l'algorithme suivant : ... il faut donc savoir décomposer un graphe en niveaux.
 Quelques propriétés des graphes distances héréditaires
Quelques propriétés des graphes distances héréditaires
6.3.1 Rappels sur la décomposition par substitution . . . . . 26. 6.3.2 Pour les graphes 2 – Un exemple de graphe avec les niveaux de distances.
 Structure multi-échelle de grands graphes de terrain
Structure multi-échelle de grands graphes de terrain
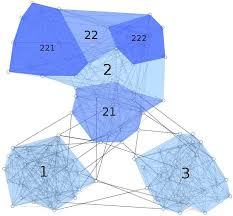
Graphe avec représentation de la décomposition niveau par niveau et de l'arbre obtenu. Les feuilles de l'arbre sont les sommets du graphe initial.
 Méthodes dOptimisation
Méthodes dOptimisation
1.1.2 Niveaux des sommets d'un graphe sans circuit . Le mouvement de mati`ere se décompose en un nombre fini de mouvements partiels chacun allant d'un.
 PLANIFICATION et Ordonnancement
PLANIFICATION et Ordonnancement
Les rangs (ou niveaux) déterminés permettent de positionner le début des différentes tâches lors de la construction du graphe.
 IT3004 Graphes et algorithmes Notes de cours et exercices - ESIEE
IT3004 Graphes et algorithmes Notes de cours et exercices - ESIEE
Exemple 1 : Soit un graphe G=(E?) avec E ={1234}et ? dé?nie par : ?(1)={124} ?(2)={31} ?(3)={4} ?(4)=0/ Iln’estpasfaciledevisualiserungraphedonnésouscetteforme Habituellementonreprésente ungrapheparundessintelqueceluidela?gure1 1pagesuivante Notonsqueplusieursdessins comme pour cet exemple peuvent représenter le même
 Les graphes - univ-reunionfr
Les graphes - univ-reunionfr
De manière générale un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication réseaux routiers interaction de diverses espèces animales circuits électriques )
 Théorie des graphes et optimisation dans les graphes - CNRS
Théorie des graphes et optimisation dans les graphes - CNRS
i(dans le cas d’un 1-graphe on aura d +(s i) =jsucc(s i) j) De même le demi-degré intérieur d’un sommet s i noté d (s i) est le nombre d’arcs arrivant à s i(dans le cas d’un 1-graphe on aura d (s i) =jpred(s i) j) Exercice : Dessiner un graphe non orienté complet à 4 sommets Quel est le degré des som-mets de ce graphe?
 Chapitre 3 - Graphes 1 Graphes et modes de représentation
Chapitre 3 - Graphes 1 Graphes et modes de représentation
Pour le rendre plus lisible il est souvent utile de représenter un graphe par niveaux Pour cela il faut déterminer le niveau de chacun des sommets du graphe Proposition Le niveau d'un sommet a autv : 0 si a n'a pas de prédécesseur 1+nmax sinon où nmax est le maximum des niveaux des prédécesseurs de a Méthode
 Searches related to décomposition d+un graphe en niveaux PDF
Searches related to décomposition d+un graphe en niveaux PDF
La treelength d’un graphe est elle aussi toujours dé?nie : la length de la décomposition constituée d’un seul sac contenant tous les sommets du grapheestégaleaudiamètredugraphe(ladistanceentrelesdeuxsommets lespluséloignés)unebornesupérieuredelatreelength Figure 5–Ungrapheetunetree-decompositiondecegraphe
Quel est le degré d’un graphe?
3.b Ordre et degré On appelleordred’un graphe le nombre de ses sommets. Ledegréd’un sommet est le nombre d’arrêtes dont il est une extrémité. Deux sommets reliés par une même arrête sont ditsadjacents.
Quel est le degré d’un graphe d’ordre 4?
b D Ce graphe comporte 4 sommets, c’est donc un graphe d’ordre 4. • Du sommet A partent 4 arrêtes. Le degré du sommet A est donc 4. • Le degré du sommet B est 3. • Le degré du sommet C est 4. • Le degré du sommet D est 1.
Quels sont les problèmes des graphes pondérés?
J 10 25 97 12 30 39 17 L’un des problèmes classiques des graphes pondérés est celui de recherche d’un trajet routier le plus court (en terme de temps ou de kilomètres). Si un graphe n’est pas pondéré, le poids de chaque arête peut être considéré comme égale à 1.
Quel est le rôle d'un graphe?
De manière générale, un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication, réseaux routiers, interaction de diverses espèces animales, circuits électriques...)
Semestre 5 { Parcours Gestion { Section B
Pr. Kh. BENMLIH
CHAPITRE 2 : Theorie des graphes et applications
I. | Quelques notions de base
I.1Denitions et representations d'un graphe
I.2Chemins dans un graphe oriente
II. | Recherche de chemin optimal
II.1Principe d'optimalite
II.2Recherche du plus court chemin a origine unique dans un graphe sans boucle et sans circuitIII. | Problemes d'ordonnancement
III.1Introduction
III.2Methode MPM : principe, construction du graphe et determination de chemin critique III.3Methode PERT : principe, construction du graphe et determination de chemin critiqueI. Quelques notions de base
I.1 Denitions et representations
I.1.1 Principales denitions
Un graphe orienteG= (X;U) est la donnee deux ensembles : - Un ensembleX=fx1;x2;;xngdont les elements sont appelessommets; - Un sous-ensembleUXXnoteU=fu1;u2;;umgdont les elements sont appelesarcs. Pour un arcu= (xi;xj), le sommetxis'appelle extremite initiale (ou origine) etxjson extremite nale (ou destination). Dans l'arc (xi;xj), on dit que le sommetxjest un successeur dexi. On dit aussi que le sommetxiest un predecesseur dexj.Lorsquexi=xj, l'arc (xi;xi) s'appelle uneboucle.
Un arc prive de son orientation s'appelleune ar^ete. Deux sommets sont ditsadjacentss'ils sont joints par un arc (ou une ar^ete), et deux arcs sont dits adjacents s'ils ont au moins une extremite commune. Unsous-grapheest obtenu par suppression d'un certain nombre de sommets (et par consequent de tous les arcs qui leur sont lies). Ungraphe partielest obtenu par suppression d'un certain nombre d'arcs. Chapitre 2Theorie des graphes et applications2I.1.2 Modes de representation d'un graphe a) Representation par dictionnaire (liste) : Il s'agit d'un tableau a entree simple ou chaque lignecorrespond a un sommet et comporte la liste de ses predecesseurs (dictionnaire des predecesseurs) ou de
ses successeurs (dictionnaire des successeurs).Exemple 1 :
b) Representation sagittale : c) Representation par la matrice d'adjacence : Considerons un grapheG= (X;U) contenantnsommets. La matrice d'adjacence (ou matrice booleenne) est une matrice carree d'ordrende terme general :
{aij= 1 si (xi;xj)2U a ij= 0 sinonReprendre l'exemple precedent :
I.2 Chemins dans un graphe oriente
Un chemin est une succession d'arcs adjacents de m^eme sens. Un circuit est un chemin ferme dans le sens ou les deux extremites initiale et nale sont confondues. Un chemin est dit de longueurp2Ns'il est constitue deparcs distincts.II. Recherche de chemin optimal
SoitG= (X;U) un graphe value ou a chaque arca2Uon associe une longueurl(a). Cette longueur peut representer une duree de parcours, un benece de transport, ... etc Le probleme du plus court chemin (respectivement du plus long chemin) entre les sommetsietjconsiste a trouver un chemin(i;j) dont la longueurl() =∑ a2(i;j)l(a) est minimale (respectivement maximale). RemarqueNous supposons que dans le cas de recherche de chemin de longueur minimale (respectivementmaximale), le graphe ne contient aucun circuit de longueur strictement negative (respectivement strict.
negative). Sinon, l'etude est sans objet.II.1 Principe d'optimalite
THEOREME. |Tout sous-chemin d'un plus court chemin(respectivement d'un plus long chemin)est un chemin de longueur minimale(respectivement maximale). II.2 Recherche du plus court chemin a origine unique dans un graphe sans boucle et sans circuit Lorsqu'on cherche un plus court chemin d'un sommet xex1a tous les autres sommets du graphe, plusieurs algorithmes peuvent ^etre appliques ( algorithme de Bellman-Ford, algorithme de Dijkstra,)selon les proprietes et la nature du graphe. Le principe de ces algorithmes etant d'affecter a chaque sommet
x iune marquemi. En n d'algorithme, cette marque represente la longueur d'un plus court chemin de l'originex1au sommet considerexi.Kh. BENMLIHTheorie des graphes et applications3Algorithme de Bellman-Ford(sans circuit, de longueurs quelconques) (1958)
Lorsque le graphe est sans circuit, on peut appliquerl'algorithme de Bellman-Fordconsistant a affecter
une marque a chaque sommet du graphe ordonne en niveaux. a)Decomposition en niveaux du graphe. D EFINITION. |On appelle niveau d'un sommetxila longueur maximale au sens des arcs allant de l'origine vers ce sommet.Procedure de determination des niveaux
* L'ensemble du niveau 0 est donne parN0=fx2X=P(x) =∅g; * D'un niveau a un autre immediatement superieur, on aNi=fx2XnNi1=P(x) =∅g; * S'arr^eter lorsque iN i=X. (Autrement dit, les niveaux de tous les sommets du graphe sont determines) RemarqueSi a une quelconque etapek0on trouve queNk=∅, cela signie que le graphe contient au moins un circuit.Le graphe ordonne en niveaux est represente dans l'ordre croissant des niveaux des differents sommets.
Lorsque l'origine n'est pas l'unique sommet de niveau 0, la suite de l'etude portera sur lesous-graphe
obtenu en eliminant tous les autres sommets de niveaux inferieurs ou egaux a celui de l'origine. Une fois la
marque de l'extremite nale est determinee, on arr^ete la procedure. b)Determination des marques: * Pour l'originex1(de niveau 0), on posem(x1) = 0 * D'un niveau a un autre immediatement superieur, on pose : m(xi) = minfm(xj) +l(xj;xi);xj2P(xi)gRemarqueDans le cas de la recherche d'un plus long chemin, on procede de la m^eme maniere en utilisant
dans l'algorithme l'operation "max" au lieu de "min". c)Identication d'un chemin de valeur optimale allant dex1axn: * On affecte a chaque sommetxjsa marque denitivemj. * On posexp=xnet on cherche les sommetsxj21(xp) veriantmj=mpl(xj;xp). * Pour chaque chemin identie, s'arr^eter lorsquex1est atteint.Exemple :
III. Problemes d'ordonnancement
III.1 Introduction
L'objectif est d'ordonner dans le temps un ensemble d'operations contribuant a la realisation d'un m^eme
projet (construction d'un b^atiment, lancement d'un produit, ... etc). Le deroulement de ces diverses t^aches doit respecter certaines contraintes de type : Chapitre 2Theorie des graphes et applications4- contrainte de succession stricte, - contrainte de date.Il s'agit donc de minimiser la duree totale de realisation du projet compte tenu des durees necessaires a la
realisation de chaque operation et des contraintes qu'elles doivent respecter. Le probleme ainsi pose peut ^etre schematise sous forme d'un graphe sans circuit selon deux modes : - la methode M.P.M.(Methode des potentiels Metra), appelee egalement methode graphe-t^aches; - la methode PERT(Programm Evaluation Research Task), appelee egalement methode graphe-etapes. Exemple: Les operations mises en jeu dans la construction d'un ensemble hydro-electrique sont noteespar les lettresa;b;;i. On suppose que toutes les contraintes sont de type contraintes de succession. Les
donnees du probleme sont resumees dans le tableau suivant :Operation
Designation
Duree (mois)
Operations prerequises
Construction des voies d'acces
a 4Travaux des terrassemets
b 6 aConstruction des b^atiments administratifs
c 4Commande du materiel electrique
d 12Construction de la centrale
e 10 b; c; dConstruction du barrage
f 24b; c
Installation des galeries et conduites forcees
g 7 aMontage des machines
h 10 e; gEssais de fonctionnement
i 3 f; h TAF : Duree minimale d'excecution du projet? Calendrier de debut d'excecution (au plus t^ot et au plus tard) des differentes t^aches? Chemin critique?III.2 Methode MPM
1. Principe
Le graphe pour ce mode de representation est construit comme suit :Chaque t^achexiest representee par un sommeti.
Toute relation d'anteriorite immediate est representee par un arc.La longueurl(i;j) d'un arc (i;j) est egale a la duree minimale qui doit s'ecouler entre le debut de la
t^achexiet le debut de la t^achexj. Lorsque les contraintes sont uniquement de type "succession stricte",
cette longueur est egale a la duree de la t^ache originexi.2. Construction du graphe MPM
Le graphe MPM est ordonne par niveaux (graphe sans circuit). Chaque sommet sera represente par un rectangle de type :ou x: designe la t^ache; T x: designe la date de debut au plus t^ot de la t^achex; T x: designe la date de debut au plus tard de la t^achex.Kh. BENMLIHTheorie des graphes et applications5On introduit a la n un sommet representant une t^ache n (notee souvent par la lettre z) auquel seront
relies tous les sommets qui n'ont pas de successeurs. Cette t^ache permettra de dater la n des travaux.
3. Determination du calendrier au plus t^ot
(Tx)Pour les sommetsxde niveau 0 : on poseTx= 0.
Pour les sommets de niveaux superieurs : on poseTx= longueur du chemin le plus long allant d'un sommet de niveau 0 a ce sommet. Autrement dit :Tx= MaxfTy+l(y;x);y2P(x)g. Par consequent,la duree minimale de realisation du projet estTzouzdesigne la t^ache nale.4. Determination du chemin critique
Le chemin critique est le chemin le plus long allant d'un sommet de niveau 0 au sommet nalz.Tout retard observe sur l'execution de l'une des t^aches situees sur le chemin critique retardera la date
a laquelle peut s'achever au plus t^ot l'ensemble des travaux du projet.5. Determination du calendrier au plus tard
(Tx)Procedure :
- On poseTz=Tz - D'un niveau a un autre inferieur, on poseTx= MinfTyl(x;y);y2S(x)g. La marge totale d'une t^ache : C'est le retard maximum que l'on peut prendre dans la mise en route d'une t^ache, sans remettre en cause la date de la n des travaux. Elle est donc egale a (TxTx).III.3 Methode PERT
1. Principe
Le graphe pour ce mode de representation est construit comme suit : Chaque t^achexest representee par un arc (i;j) dont la longueur est egale a la duree de la t^ache. Chaque sommet du graphe est une etape signiant que : - toutes les t^aches qui arrivent sont achevees, - toutes les t^aches qui partent peuvent commencer.Remarque: La representation de certaines relations d'anteriorite necessite l'introduction de certaines
t^achesctivesde duree 0.Exemple 1 :
Exemple 2 :
2. Construction du graphe PERT
La decomposition en niveaux n'est pas demandee puisque les sommets ne correspondent pas aux t^aches. Chaque sommet sera represente par un cercle de type :ou x: designe le numero de l'etape; Chapitre 2Theorie des graphes et applications6tx: designe la date attendue de l'etapex; t x: designe la date limite de l'etapex. On introduit un sommet initial d'ou partent toutes les t^aches sans contrainte d'anteriorite; et un sommet nal auquel arrivent toutes les t^aches sans suivantes. Ce sommet permettra de dater la n des travaux.3. Determination du calendrier au plus t^ot
Pour le sommet initialn◦1, on poset1= 0.
Pour les sommetsxsuivants :tx= longueur du chemin le plus long allant d'un sommet 1 au sommet x. c'est la date attendue de de letapex; elle est egale a la date de debut au plus t^ot de toutes les t^aches
qui partent dex.Donc, si une t^acheKest representee par un arc (i;j), alors la date de debut au plus t^ot pour cette t^ache
estTK=ti.4. Determination du chemin critique
M^eme procedure que dans la methode MPM.
5. Determination du calendrier au plus tard
Procedure :
- Pour le sommet nalz, on posetz=tz - pour les autres sommets, on procede de la m^eme maniere que pour le calcul desTxdans la methode MPM. - La date de debut au plus tard pour la t^acheK, representee par l'arc (i;j), de dureedKestTK= t jdK. La marge totale d'une t^acheKest donnee par (TKTK).quotesdbs_dbs44.pdfusesText_44[PDF] de l'année 1789 ? l'exécution du roi cm1
[PDF] graphe d'ordonnancement
[PDF] sujet algorithme bts sio corrigé
[PDF] calcul matrice booléenne
[PDF] calcul matriciel bts
[PDF] prise de note rapide tableau abréviations
[PDF] sauzay programme
[PDF] programme voltaire
[PDF] un petit paragraphe sur l'environnement
[PDF] exemple de texte argumentatif sur l'environnement
[PDF] texte sur l'environnement
[PDF] texte argumentatif sur l'environnement 4am
[PDF] protection de l'environnement définition
[PDF] graphe probabiliste calculatrice
