Validation et optimisation dune décomposition hiérarchique de
24 janv. 2012 Dans ce cadre une généralisation de cette mesure de qualité au cas multi-niveaux est introduite. Nous testons notre méthode sur des graphes ...
Théorie des graphes
7 avr. 2011 Théorie des graphes. 7 avril 2011. 75 / 125. Page 76. Graphes sans circuit. S-séquence d'un graphe - Décomposition par niveaux. Définition. Soit ...
CHAPITRE 2 : Théorie des graphes et applications
une marque `a chaque sommet du graphe ordonné en niveaux. a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur
GRAPHES
2 avr. 2008 Graphes sans circuit. Lorsque le graphe est sans circuit il peut être décomposé en niveaux. La longueur du chemin de la racine `a tous les ...
Décomposition algorithmique des graphes
23 mai 2007 composition en branches d'un hyper-graphe planaire une décomposition de ... au niveau de ses extrémités et uniquement à cet endroit. Comme une ...
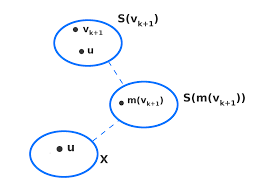Étude dalgorithmes de décomposition de graphes
1 sept. 2020 Il nous faut aussi définir la famille des graphes chordaux car ils sont étroitement liés aux tree-decompositions. Étant donné un graphe G un ...
Théorie des graphes DUT Informatique semestre 2
3 févr. 2014 courts dans un graphe il faut donc savoir décomposer un graphe en niveaux. È2.8 Décomposition en niveau d'un graphe sans circuit : 1. 2. 3. 4.
Chapitre 6 Décompositions arborescentes†
sans arêtes communes et ces sous-graphes sont « recollés » au niveau de leurs Nous venons de définir un opérateur de décomposition d'un graphe en deux sous- ...
Les plans dexpériences par la méthode TAGUCHI
niveaux décomposé en nombre premier (l'interaction BC à 6 niveaux a été Pour construire 2 colonnes à 4 niveaux il faut partir d'un graphe linéaire.
Théorie des graphes
7 avr. 2011 S-séquence d'un graphe - Décomposition par niveaux. 5 Probl`eme du plus court chemin. L. Sais (Algorithmique & Programmation 5).
Corrigé TD1 13-14
À partir de ces listes on obtient la décomposition par niveaux : S0 = {E H}
CHAPITRE 2 : Théorie des graphes et applications
a) Décomposition en niveaux du graphe. DÉFINITION. — On appelle niveau d'un sommet xi la longueur maximale au sens des arcs allant de.
Table des matières
2 Décomposition des graphes Décomposition basée sur la matrice de la fermeture transitive ... décomposition d'un graphe sans circuit en niveaux.
Théorie des graphes et optimisation dans les graphes Table des
le parcours en largeur consiste à explorer les sommets du graphe niveau par Un projet est généralement décomposé en différentes tâches à effectuer.
Théorie des graphes DUT Informatique semestre 2
3 fév. 2014 Pour décomposer en niveau un graphe G on utilisera l'algorithme suivant : ... il faut donc savoir décomposer un graphe en niveaux.
Quelques propriétés des graphes distances héréditaires
6.3.1 Rappels sur la décomposition par substitution . . . . . 26. 6.3.2 Pour les graphes 2 – Un exemple de graphe avec les niveaux de distances.
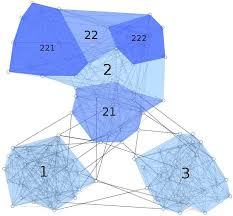
Structure multi-échelle de grands graphes de terrain
Graphe avec représentation de la décomposition niveau par niveau et de l'arbre obtenu. Les feuilles de l'arbre sont les sommets du graphe initial.
Méthodes dOptimisation
1.1.2 Niveaux des sommets d'un graphe sans circuit . Le mouvement de mati`ere se décompose en un nombre fini de mouvements partiels chacun allant d'un.
PLANIFICATION et Ordonnancement
Les rangs (ou niveaux) déterminés permettent de positionner le début des différentes tâches lors de la construction du graphe.
IT3004 Graphes et algorithmes Notes de cours et exercices - ESIEE
Exemple 1 : Soit un graphe G=(E?) avec E ={1234}et ? dé?nie par : ?(1)={124} ?(2)={31} ?(3)={4} ?(4)=0/ Iln’estpasfaciledevisualiserungraphedonnésouscetteforme Habituellementonreprésente ungrapheparundessintelqueceluidela?gure1 1pagesuivante Notonsqueplusieursdessins comme pour cet exemple peuvent représenter le même
Les graphes - univ-reunionfr
De manière générale un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication réseaux routiers interaction de diverses espèces animales circuits électriques )
Théorie des graphes et optimisation dans les graphes - CNRS
i(dans le cas d’un 1-graphe on aura d +(s i) =jsucc(s i) j) De même le demi-degré intérieur d’un sommet s i noté d (s i) est le nombre d’arcs arrivant à s i(dans le cas d’un 1-graphe on aura d (s i) =jpred(s i) j) Exercice : Dessiner un graphe non orienté complet à 4 sommets Quel est le degré des som-mets de ce graphe?
Chapitre 3 - Graphes 1 Graphes et modes de représentation
Pour le rendre plus lisible il est souvent utile de représenter un graphe par niveaux Pour cela il faut déterminer le niveau de chacun des sommets du graphe Proposition Le niveau d'un sommet a autv : 0 si a n'a pas de prédécesseur 1+nmax sinon où nmax est le maximum des niveaux des prédécesseurs de a Méthode
Searches related to décomposition d+un graphe en niveaux PDF
La treelength d’un graphe est elle aussi toujours dé?nie : la length de la décomposition constituée d’un seul sac contenant tous les sommets du grapheestégaleaudiamètredugraphe(ladistanceentrelesdeuxsommets lespluséloignés)unebornesupérieuredelatreelength Figure 5–Ungrapheetunetree-decompositiondecegraphe
Quel est le degré d’un graphe?
3.b Ordre et degré On appelleordred’un graphe le nombre de ses sommets. Ledegréd’un sommet est le nombre d’arrêtes dont il est une extrémité. Deux sommets reliés par une même arrête sont ditsadjacents.
Quel est le degré d’un graphe d’ordre 4?
b D Ce graphe comporte 4 sommets, c’est donc un graphe d’ordre 4. • Du sommet A partent 4 arrêtes. Le degré du sommet A est donc 4. • Le degré du sommet B est 3. • Le degré du sommet C est 4. • Le degré du sommet D est 1.
Quels sont les problèmes des graphes pondérés?
J 10 25 97 12 30 39 17 L’un des problèmes classiques des graphes pondérés est celui de recherche d’un trajet routier le plus court (en terme de temps ou de kilomètres). Si un graphe n’est pas pondéré, le poids de chaque arête peut être considéré comme égale à 1.
Quel est le rôle d'un graphe?
De manière générale, un graphe permet de représenter des objets ainsi que les relations entre ses éléments (par exemple réseau de communication, réseaux routiers, interaction de diverses espèces animales, circuits électriques...)
Christine Solnon
Table des matières
1 Motivations 3
2 Définitions 4
3 Représentation des graphes 8
3.1 Représentation par matrice d"adjacence . . . . . . . . . . . . . . . . . . . . . . 8
3.2 Représentation par listes d"adjacence . . . . . . . . . . . . . . . . . . . . . . . . 8
4 Cheminements et connexités 10
4.1 Notions de chemin, chaine, cycle et circuit . . . . . . . . . . . . . . . . . . . . . 10
4.2 Fermeture transitive d"un graphe . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.3 Notions de connexité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
4.4 Notion de graphe eulérien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
4.5 Notion de graphe hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
5 Arbres et arborescences 17
6 Graphes planaires 20
7 Coloriage de graphes, cliques et stables 23
8 Parcours de graphes 25
8.1 Arborescence couvrante associée à un parcours . . . . . . . . . . . . . . . . . . 26
8.2 Parcours en largeur (Breadth First Search = BFS) . . . . . . . . . . . . . . . . . 26
8.3 Applications du parcours en largeur . . . . . . . . . . . . . . . . . . . . . . . . 27
8.4 Parcours en profondeur (Depth First Search = DFS) . . . . . . . . . . . . . . . . 28
8.5 Applications du parcours en profondeur . . . . . . . . . . . . . . . . . . . . . . 29
19 Plus courts chemins 31
9.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
9.2 Algorithme de Dijkstra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
9.3 Algorithme de Bellman-Ford . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
9.4 Synthèse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
10 Arbres couvrants minimaux (ACM) 39
11 Réseaux de transport 42
12 Planification de projet par les réseaux 47
12.1 Coût et durée d"une tâche . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
12.2 Contraintes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
12.3 Modélisation des contraintes de précédence par un graphe . . . . . . . . . . . . . 48
12.4 Durée minimale d"exécution . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
12.5 Date au plus tard . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
12.6 Marge totale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
12.7 Chemins et tâches critiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
13 Pour en savoir plus 52
21 Motivations
Pour résoudre de nombreux problèmes concrets, on est amené à tracer sur le papier des petits
dessins qui représentent (partiellement) le problème à résoudre. Bien souvent, ces petits dessins se
composent de points et de lignes continues reliant deux à deux certains de ces points. On appellera
ces petits dessins desgraphes, les points dessommetset les lignes desarcsouarêtes, selon que la relation binaire sous-jacente est orientée ou non. Quelques exemples de modélisation par des graphesRéseaux routiers :Le réseau routier d"un pays peut être représenté par un graphe dont les som-
non orienté et on reliera par une arête tout couple de sommets correspondant à deux villes reliées
par une route (si l"on considère en revanche que certaines routes sont à sens unique, on utilisera un
graphe orienté). Ces arêtes pourront être valuées par la longueur des routes correspondantes. Etant
donné un tel graphe, on pourra s"intéresser, par exemple, à la résolution des problèmes suivants :
- Quel est le plus court chemin, en nombre de kilomètres, passant par un certain nombre de villes données? - Quel est le chemin traversant le moins de villes pour aller d"une ville à une autre? - Est-il possible de passer par toutes les villes sans passer deux fois par une même route?Processus à étapes :Certains problèmes peuvent être spécifiés par un état initial, un état final,
un certain nombre d"états intermédiaires et des règles de transition précisant comment on peut
passer d"un état à l"autre. Résoudre le problème consiste alors à trouver une suite de transitions
permettant de passer de l"état initial à l"état final. Beaucoup de jeux et autres "casse-tête" peuvent
être modélisés ainsi. Considérons, par exemple, le problème du chou, de la brebis et du loup :
Un brave homme se trouve au bord d"une rivière qu"il souhaite traverser, en compa- gnie d"un loup, d"une brebis et d"un chou. Malheureusement, il ne dispose que d"une petite barque, ne pouvant porter en plus de lui-même qu"un seul de ses compagnons (le loup ou la brebis ou le chou). Bien sûr, la brebis refuse de rester seule avec le loup, tandis que le chou refuse de rester seul avec la brebis. Comment peut-il s"y prendre pour traverser la rivière avec ses trois compagnons et continuer son chemin?L"état initial est l"état où tout le monde est sur la rive gauche de la rivière, tandis que l"état final
est l"état où tout le monde est sur la rive droite de la rivière. La règle de transition est la suivante :
si l"homme est sur une rive avec certains de ses compagnons, alors il peut passer sur l"autre rive, soit seul, soit accompagné par un seul de ses compagnons se trouvant sur la même rive que lui, sous réserve qu"il ne laisse pas le loup seul avec la brebis, ou la brebis seule avec le chou. Onpeut modéliser ce problème par un graphe non orienté, dont les sommets représentent les états
possibles, et les arêtes le fait qu"on peut passer d"un état à l"autre par une transition. On obtient
alors le graphe non orienté suivant : 3 HCBLL B CH L CH BL C HBL H C BL H BC B L H CB HL C H B CLC BLHLB HC
C H LBCH BLH
BL C H LBCEtat initialEtat finaloù le loup est représenté par la lettreL, le chou parC, la brebis parBet l"homme parH, et où un
état est représenté par un cercle coupé en deux demi-cercles représentant les rives gauche et droite
de la rivière.Etant donné un tel graphe, on pourra chercher un chemin allant de l"état initial à l"état final.
Automates finis :Un automate fini permet de reconnaître un langage régulier et peut être repré-
senté par un graphe orienté et étiqueté. Par exemple, l"automate fini reconnaissant le langage des
mots de la formeanbm(les mots composés d"une suite de "a" suivie d"une suite de "b") peut être représenté par le graphe suivant132baa
bCe graphe possède 3 sommets et 4 arcs, chaque arc étant étiqueté par un symbole (aoub). Etant
donné un tel graphe, on peut s"intéresser, par exemple, à la résolution des problèmes suivants :
- Existe-t-il un chemin allant du sommet initial (1) au sommet final (3)? - Quel est le plus court chemin entre deux sommets donnés?- Existe-t-il des sommets inutiles, par lesquels aucun chemin allant du sommet initial à un sommet
final ne peut passer?2 Définitions
De façon plus formelle, ungrapheest défini par un coupleG= (S;A)tel que -Sest un ensemble fini de sommets, -Aest un ensemble de couples de sommets(si;sj)2S2.Un graphe peut être orienté ou non :
- Dans ungraphe orienté, les couples(si;sj)2Asont orientés, c"est à dire que(si;sj)est un couple ordonné, oùsiest le sommet initial, etsjle sommet terminal. Un couple(si;sj)est appelé unarc, et est représenté graphiquement parsi!sj.Par exemple,
4 1 2 3456représente le graphe orientéG= (S;A)avecS=f1;2;3;4;5;6get
- Dans ungraphe non orienté, les couples(si;sj)2Ane sont pas orientés, c"est à dire que(si;sj)est équivalent à(sj;si). Une paire(si;sj)est appelée unearête, et est représentée
graphiquement parsi-sj.Par exemple,
2 45 361représente le graphe non orientéG= (S;A)avecS=f1;2;3;4;5;6get
A=f(1;2);(1;5);(5;2);(3;6)g.
Terminologie
- L"ordred"un graphe est le nombre de ses sommets. - Uneboucleest un arc ou une arête reliant un sommet à lui-même. - Un graphe non-orienté est ditsimples"il ne comporte pas de boucle, et s"il ne comporte jamais plus d"une arête entre deux sommets. Un graphe non orienté qui n"est pas simple est unmulti- graphe. Dans le cas d"un multi-graphe,An"est plus un ensemble mais un multi-ensemble d"arêtes. On se restreindra généralement dans la suite aux graphes simples. - Un graphe orienté est unp-graphes"il comporte au plusparcs entre deux sommets. Le plus souvent, on étudiera des 1-graphes. - Ungraphe partield"un graphe orienté ou non est le graphe obtenu en supprimant certains arcs ou arêtes. - Unsous-graphed"un graphe orienté ou non est le graphe obtenu en supprimant certains som- mets et tous les arcs ou arêtes incidents aux sommets supprimés. - Un graphe orienté est ditélémentaires"il ne contient pas de boucle. - Un graphe orienté est ditcomplets"il comporte un arc(si;sj)et un arc(sj;si)pour tout couple de sommets différentssi;sj2S2. De même, un graphe non-orienté est dit complet s"il comporte une arête(si;sj)pour toute paire de sommets différentssi;sj2S2.Notion d"adjacence entre sommets :
- Dans un graphe non orienté, un sommetsiest ditadjacentà un autre sommetsjs"il existe une arête entresietsj. L"ensemble des sommets adjacents à un sommetsiest défini par : adj(si) =fsj=(si;sj)2Aou (sj;si)2Ag - Dans un graphe orienté, on distingue les sommetssuccesseursdes sommetsprédécesseurs: succ(si) =fsj=(si;sj)2Ag pred(si) =fsj=(sj;si)2Ag 5Notion de degré d"un sommet :
- Dans un graphe non orienté, ledegréd"un sommet est le nombre d"arêtes incidentes à ce som-
met (dans le cas d"un graphe simple, on aurad(si) =jadj(si)j). - Dans un graphe orienté, ledemi-degré extérieurd"un sommetsi, notéd+(si), est le nombre d"arcs partant desi(dans le cas d"un 1-graphe, on aurad+(si) =jsucc(si)j). De même, le demi-degré intérieurd"un sommetsi, notéd(si), est le nombre d"arcs arrivant àsi(dans le cas d"un 1-graphe, on aurad(si) =jpred(si)j). Exercice :Dessiner un graphe non orienté complet à 4 sommets. Quel est le degré des som-mets de ce graphe? Combien d"arêtes possède-t-il? Généralisez ces résultats à un graphe simple
complet ayantnsommets.Correction :2 41
3Ce graphe possède 6 arêtes et chaque sommet du graphe est de degré 3.
De façon plus générale, étant donné un graphe simple complet ayantnsommets, chaque sommet
étant relié auxn1autres sommets, le degré de chaque sommet estn1. Le nombre d"arêtesd"un graphe est égal à la moitié de la somme des degrés de tous ses sommets. Par conséquent, un
graphe simple complet ayantnsommets auran(n1)=2arêtes. Exercice :On considère le graphe orientéG= (S;A)tel queS=f1;2;3;4;5g
1. représenter graphiquement ce graphe,
2. donner le demi-degré extérieur de 2 et le demi-degré intérieur de 4,
3. donner les sommets prédécesseurs de 4 et les sommets successeurs de 2,
4. donner un graphe partiel et un sous-graphe de ce graphe.
Correction :
1. Une représentation graphique du graphe est13
4522.d+(2) = 3; d(4) = 2
3. pred(4) = {1, 2}, succ(2) = {2, 3, 4}
4. Exemple de graphe partiel et de sous-graphe :
6 13452Graphe partiel
quotesdbs_dbs44.pdfusesText_44[PDF] de l'année 1789 ? l'exécution du roi cm1
[PDF] graphe d'ordonnancement
[PDF] sujet algorithme bts sio corrigé
[PDF] calcul matrice booléenne
[PDF] calcul matriciel bts
[PDF] prise de note rapide tableau abréviations
[PDF] sauzay programme
[PDF] programme voltaire
[PDF] un petit paragraphe sur l'environnement
[PDF] exemple de texte argumentatif sur l'environnement
[PDF] texte sur l'environnement
[PDF] texte argumentatif sur l'environnement 4am
[PDF] protection de l'environnement définition
[PDF] graphe probabiliste calculatrice
