Examen corrigé PDF

Intégrales doubles

16 oct. 2015 Exercice 32 [ 00111 ] [Correction]. Calculer l'aire de la portion ... Par le théorème de Fubini (avec ici f ⩾ 0) ces deux intégrales sont égales ...

Cours et exercices corrigés

3.4 Exercices sur les intégrales multiples . L'objectif de la troisième partie est d'introduire la notion de l'intégrale double et comment calculer.

Quelques corrigés dexercices des feuilles 5 et 6

Quelques corrigés d'exercices des feuilles 5 et 6. Calculer l'intégrale double Avec la deuxième cela donne la même chose (et les calculs à faire sont à peu ...

Intégration etÉquations différentielles Licence Mathématiques

avec a b > 0. Exercice 20 (calcul d'intégrales doubles par changement de variables

Exercices de mathématiques - Exo7

Même question avec ω = y2dx+x2dy. Correction ▽. [005907]. Exercice 3 **. Calculer les intégrales multiples suivantes. 1

EN - EXERCICES SUR LES INTEGRALES MULTIPLES

f(x y)dxdy . Page 4. EN 4. Corrigé des exercices sur les intégrales multiples On calcule alors l'intégrale double. I = ∫∫. D1. 1. 3 (. 1 − (x + y)3) dxdy ...

examens-corriges-integrales-multiples.pdf

Exercice 1. (a) Avec : D := {(x y) ∈ R2 Quel nom amusant pourrait-on lui attri- buer ? (b) Avec un paramètre réel α > 0

Intégration Pascal Lainé 1

Et on pourra utiliser une forme de l'inégalité triangulaire. Allez à : Correction exercice 8. Exercice 9. Soient et deux réels fixés avec <

Calcul des structures hyperstatiques Cours et exercices corrigés

Soit le treillis plan de la Figure 5.6 où on change l'appui B (doubles réactions) par un appui simple avec une seule réaction et on ajoute une autre barre entre

Quelques corrigés dexercices des feuilles 5 et 6

2011-2012. Quelques corrigés d'exercices des feuilles 5 et 6. Calculer l'intégrale double. ??. R xcos(x + y) dxdy R région triangulaire de som-.

Corrigé de la feuille TD N?4 - semaine du 17/03/2008 (les énoncés

Exercice 2. (calculer une intégrale double sur un triangle). Soit ? le domaine de R2 bordé par le triangle dont les sommets sont les points A

Intégration etÉquations différentielles Licence Mathématiques

Annexe C. Annales 2011-2012 Texte et corrigé de l'examen de session 1 Exercice 20 (calcul d'intégrales doubles par changement de variables

Exercices de mathématiques - Exo7

Même question avec ? = y2dx+x2dy. Correction ?. [005907]. Exercice 3 **. Calculer les intégrales multiples suivantes. 1

Exercices de mathématiques - Exo7

calculer les intégrales ? 1. 0 f(x)dx ? 2. 1g(x)dx et ? x. 0 h(t)dt. Indication ?. Correction ?. Vidéo ?. [002082]. Exercice 3.

Exercices sur les intégrales doubles.

2012/2013. Semestre de printemps. Université Lyon I. Calcul différentiel et intégral. Exercices sur les intégrales doubles. Exercice 1. Calculer.

Intégrales doubles

16 oct. 2015 Intégrales doubles. Calculs d'intégrales doubles. Exercice 1 [ 01947 ] [Correction]. Calculer. I = ??. D xy dx dy avec.

Intégrales de fonctions de plusieurs variables

le long d'une courbe fermée C peuvent s'exprimer comme des intégrales doubles sur la région du plan entourée par C (c'est la formule de Green-Riemann).

Examen corrigé

(b) Avec un paramètre réel ? > 0 on introduit l'intégrale double : I?(?) := En distinguant les deux cas ? = 1 et ? = 1

Examen corrigé

FrançoisDEMARÇAY

Département de Mathématiques d"Orsay

Université Paris-Saclay, France

1. Examen 1

Exercice 1.

(a) Avec :

D:=(x;y)2R2: 16y62;06x6y2;

calculer :

I:=Z Z

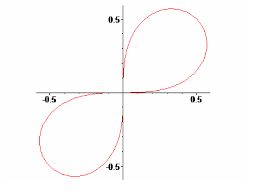
D ex=y2dxdy: Exercice 2.Pour tout" >0, on définit le sous-ensemble du plan euclidien : A ":=(x;y)2R2:"26x2+y261: (a)Représenter graphiquement cet ensembleA". Quel nom amusant pourrait-on lui attri- buer? (b)Avec un paramètre réel >0, on introduit l"intégrale double : I "() :=Z Z A "dxdy x2+y2: En distinguant les deux cas= 1et6= 1, calculer la valeur deI"().Indication:Passer aux coordonnées polaires, et trouver, lorsque6= 1: I "() =constante 11" 22
où la constante inconnue est à déterminersans erreur de calcul. (c)En déduire que : lim "!>0I"() =8 >>>:1pour0< <1; +1si= 1; +1lorsque1< : 1

2 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Saclay, FranceExercice 3.(a) Représenter le compact d"intégrationA:=(x;y;z)2R3:x;y2

[0;1]; z2[1;2]. (b)Calculer l"intégrale tripleRRR Axyz

2dxdydz.

(c)Représenter le compact d"intégrationB:=(x;y;z)2R3: 06z61;z6x6 z;z6y6z. (d)Calculer son volumeVolumeB=RRR

B1dxdydz.

(e)Calculer l"intégrale tripleRRR

Bz dxdyz.

2.Corrigé de l"examen 1 32. Corrigé de l"examen 1

Exercice 1.

(a) On a : I=Z 2 1 dyZ y2 0 ex=y2dx=Z 2 1 dyh y

2ex=y2iy2

0 =Z 2 1 dy y

2e1y2e0

e11Z2 1 y2dy=e1113 y3 2 1 =e1183 13 =73 e11:

Exercice 2.

(a) Il s"agit d"undisque transpercé, ou, si on préfère, d"unanneau gras.R 2 A 1 0 (b)Le changement de variables : x=rcosety=rsin; avec bien sûr pour notre bel anneau dodu : "6r61; et aussi, évidemment : 0662;
en rappelant que : dxdy=rdrd; conduit à réexprimer l"intégrale recherchée sous une forme : I "() =Z 2 0 dZ 1 "rdrr 2=Z 2 0 dZ 1 "drr 21;

4 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Saclay, Francequi devient facile à calculer, mais il faut distinguer le cas= 1:

I "() =Z 2 0 dZ 1 "drr =Z 2 0 dh logri 1 =Z 2 0 log1 log" d =2log"(>0); du cas6= 1, où, pour trouver une primitive, on peutéviterd"avoir à utiliser une fonction compliquée comme le logarithme : I "() =Z 2 0 dZ 1 r2+1dr Z 2 0 d12+ 2r2+2 1 =Z 2 0 d12+ 212+ 2"2+2 222
1 +1" 22
1 11" 22
(c)Quand0< <1, on constate lorsque">!0grâce à la positivité de l"exposant de" que : I "() =1

1"2(1)|{z}

!0 !1:

Puis, pour= 1, il est clair que :

I "(1) =2log"">!0! 1: Enfin, quand >1, on doit ré-écrire le résultat obtenu afin de mieux voir qu"on a effectivement : I "() =1|{z} >0 1" 2(1)1 ">!0! 1:

Exercice 3.

(a) Il s"agit d"un cube de côté1.

2.Corrigé de l"examen 1 5(b)Par séparation des variables, il vient aisément :Z Z Z

Axyz

2dxdydz=Z

1 0 xdxZ 1 0 y dyZ 2 1dzz

2=hx22

i 1 0h y22 i 1 0h 1z i 2 1 =12 12 12 +11 =18 (c)Pour chaque hauteurz2[0;1]fixée, la tranche : B z= [z;z][z;z] fzg est un carré horizontal de côté2z.(d)Grâce à un théorème du cours :

VolumeB=Z Z Z

1dxdydz=Z

1 0 dzZ Z B zdxdy=Z 1 0

AireBzdz

Z 1

02z2dz=h43

z3i1 0=43 (e)De la même façon :Z Z Z B z dxdydz=Z 1 0 z dzZ Z B zdxdy=Z 1 0 zAireBzdz Z 1 0 z2z2dz=Z 1 0

4z3dz=h

z 4i1 0= 1:quotesdbs_dbs7.pdfusesText_13

[PDF] Examen corrigé

Examen corrigé

FrançoisDEMARÇAY

Département de Mathématiques d"Orsay

Université Paris-Saclay, France

1. Examen 1

Exercice 1.

D:=(x;y)2R2: 16y62;06x6y2;

I:=Z Z

2 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Saclay, FranceExercice 3.(a) Représenter le compact d"intégrationA:=(x;y;z)2R3:x;y2

2dxdydz.

B1dxdydz.

Bz dxdyz.

2.Corrigé de l"examen 1 32. Corrigé de l"examen 1

Exercice 1.

2ex=y2iy2

2e1y2e0

Exercice 2.

4 FrançoisDEMARÇAY, Département de Mathématiques d"Orsay, Université Paris-Saclay, Francequi devient facile à calculer, mais il faut distinguer le cas= 1:

1"2(1)|{z}

Puis, pour= 1, il est clair que :

Exercice 3.

2.Corrigé de l"examen 1 5(b)Par séparation des variables, il vient aisément :Z Z Z

2dxdydz=Z

2=hx22

VolumeB=Z Z Z

1dxdydz=Z

AireBzdz

02z2dz=h43

4z3dz=h