[PDF] Exercice : coupes du cube Solution : coupes du cube

View - Download Exercice : coupes du cube Solution : coupes du cube

Previous PDF

Next PDF

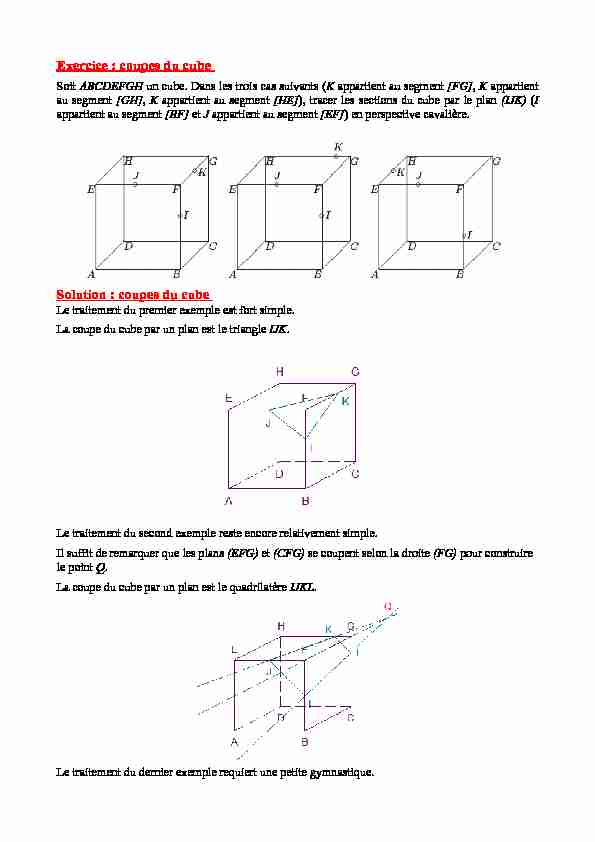
Exercice : coupes du cube Soit ABCDEFGH un cube. Dans les trois cas suivants (K appartient au segment [FG], K appartient

au segment [GH], K appartient au segment [HE]), tracer les sections du cube par le plan (IJK) (I

appartient au segment [BF] et J appartient au segment [EF]) en perspective cavalière. Solution : coupes du cube Le traitement du premier exemple est fort simple. La coupe du cube par un plan est le triangle IJK.

Le traitement du second exemple reste encore relativement simple. Il suffit de remarquer que les plans (EFG) et (CFG) se coupent selon la droite (FG) pour construire

le point Q. La coupe du cube par un plan est le quadrilatère IJKL. Le traitement du dernier exemple requiert une petite gymnastique. Il suffit de remarquer que les plans (EFG) et (CFG) se coupent selon la droite (FG) pour construire le point Q. Aussi, les plans (ABC) et (ABF) se coupent selon la droite (AB) pour construire le point R. Et encore, les plans (BCG) et (HCG) se coupent selon la droite (CG) pour construire le point S. La coupe du cube par un plan est l'hexagone IJKLMN.

Remarque : en déplaçant quelque peu le point I on aurait également pu voir une coupe pentagonale.Remarque : au lieu de ne considérer ce problème que comme un problème d'intersection, j'aurais pu

aussi utiliser la propriété qui dit qu'un plan coupe des plans parallèles en des droites parallèles. Exercice [Lyon, 2004]

On fixe un cube ABCDEFGH, d'arête 1. Une représentation du cube en perspective cavalière et son

patron sont donnés sur le document-réponse que l'on remettra avec la copie. Par exemple, le

sommet A du cube est représenté par les points A1, A2, A3 du patron.On appelle "distance" entre deux points M et N de la surface du cube, la longueur du plus court

chemin tracé sur la surface du cube et qui relie ces deux points. Pour ne pas confondre la "distance"

avec la distance usuelle, on la notera d(M,N). Par exemple, la "distance" de G à C est 1, car le plus

court chemin qui les relie est l'arête [GC]. En revanche, la "distance" de G à A est strictement plus

grande que la longueur usuelle de la diagonale [AG] du cube.1) Compléter le patron en nommant tous les sommets du cube. (On ne demande pas de justifications

pour cette question.)2) a) Tracer, en rouge sur le patron, l'ensemble des points qui représentent des points de la ligne

brisée ACG (réunion des segments [AC] et [CG]).

2) b) Calculer la longueur l de la ligne brisée ACG.

2) c) Soit J le point de la ligne brisée ACG qui est à mi-chemin de A et G, c'est-à-dire tel que d(A,J)

= AJ = l/2.

Décrire, justifier et effectuer une construction du point J sur le patron.3) Décrire et représenter sur le patron l'ensemble des points M de la surface du cube qui sont à la

même "distance" de G que C, c'est-à-dire tels que d(G,M) = d(G,C).

4) a) Parmi les chemins qui relient les sommets A et G, et qui sont totalement contenus dans les

faces ABCD et CDHG, on considère le plus court. Le tracer en bleu sur le patron, puis sur le cube

en perspective, en précisant chaque étape de la construction.4) b) Quelle est la longueur de ce chemin ?Document-réponse à rendre avec la copieSolution [Lyon, 2004]

1) Compléter le patron en nommant tous les sommets du cube. (On ne demande pas de justifications

pour cette question.)Je peux compléter face par face ...

2) a) Tracer, en rouge sur le patron, l'ensemble des points qui représentent des points de la ligne

brisée ACG (réunion des segments [AC] et [CG]).

Je dois donc juste tracer chacun des segments [AC] et [CG] sur le patron.2) b) Calculer la longueur l de la ligne brisée ACG.

2) c) Soit J le point de la ligne brisée ACG qui est à mi-chemin de A et G, c'est-à-dire tel que d(A,J)

= AJ = l/2.

Décrire, justifier et effectuer une construction du point J sur le patron.Algorithme de construction (construction en vert).Je trace le petit arc de cercle Γ de centre C et de rayon [CG1] et d'extrémités G1 et G2.

Je prolonge le segment [A2C] de manière à construire le point Ω comme point de concours de Γ et

de la droite (A2C). J'ai ainsi construit un segment [A2Ω] de longueur l. A la règle et au compas, je construis le milieu J du segment [A2Ω].

J'ai ainsi construit un point J qui est tel que d(A,J) = AJ = l/2 et qui appartient à la ligne brisée ACG

même "distance" de G que C, c'est-à-dire tels que d(G,M) = d(G,C). J'ai d(G,C)=1. On me demande donc l'ensemble des points tels que d(G,M) = 1.

Il suffit de réduire l'étude à chacune des faces du cube et d'utiliser la définition du cercle, à savoir

"le cercle de centre G et de rayon 1 est l'ensemble des points du plan en question qui sont à distance

(usuelle) de G égale à 1.

L'ensemble M de la surface du cube qui sont à la même "distance" de G que C est la réunion des

trois petits arcs de cercles suivants (représentation en rose) : le petit arc de cercle de centre G1 et de rayon 1 et d'extrémités F1 et C,

le petit arc de cercle de centre G2 et de rayon 1 et d'extrémités C et H, le petit arc de cercle de centre G1 et de rayon 1 et d'extrémités H et F2.

4) a) Parmi les chemins qui relient les sommets A et G, et qui sont totalement contenus dans les

faces ABCD et CDHG, on considère le plus court. Le tracer en bleu sur le patron, puis sur le cube

en perspective, en précisant chaque étape de la construction.Algorithme de construction (construction en bleu).

Sur le patron ...

Je trace le segment [A2G2].

Soit Θ le point de concours des droites (CD) et (A2G2). En utilisant le théorème de Thalès avec les

droites parallèles (BA2) et (CΘ) (qui sont parallèles comme côtés opposés du carré ABCD) et les

sécantes (A2G2) et (BG2) (la droite (BG2) passe par C car BCG2=BCD+DCG2= 90° +

90° = 180° comme somme d'angles de carrés), on démontre que CΘ = 1/2 et donc Θ est milieu du

segment [CD].

Sur la perspective ...

A la règle et au compas, je construis le milieu Θ du segment [CD].

Je trace ensuite les segments [AΘ] et [ΘG].

4) b) Quelle est la longueur de ce chemin ?Le théorème de Pythagore appliqué au triangle A2BG2, rectangle en B (car

A2BG2= 90° comme

angle d'un carré), donne que la longueur du chemin concerné qui n'est autre que A2G2 se calcule par

Exercice [Martinique, 2000] On considère une famille (F) de quadrilatères définie comme suit : Un quadrilatère ABCD appartient à (F) s'il est convexe et si ses diagonales [AC] et [BD]

sont perpendiculaires.

1. Pour chacune des affirmations suivantes dire si elle est vraie ou fausse. Argumenter la réponse. 1.a) Tous les rectangles appartiennent à (F).

1.b) Certains éléments de (F) sont des parallélogrammes. 2. On considère un quadrilatère ABCD de (F). Soient E, F, G et H les milieux respectifs de [AB],

[BC], [CD] et [DA].

2.a) Quelle est la nature du quadrilatère EFGH ? Le démontrer. 2.b) Quelle est la condition supplémentaire à imposer à ABCD pour que EFGH soit un carré ?

Le justifier. 3. On considère un quadrilatère ABCD de (F) tel que AC = BD = 10 cm, AB = 6 cm et l'angle

ABCest droit. 3.a) Construire à la règle et au compas, le quadrilatère ABCD.

3.b) Si O est le point d'intersection des diagonales [AC] et [BD], calculer BC puis BO.

3.c) La figure obtenue est le début d'un patron d'un tétraèdre BADC dont ABC et ACD

représentent deux faces perpendiculaires (si ACD est la base, [OB] est la hauteur du

tétraèdre). 3.c)i) Montrer que le triangle BOD est rectangle. En utilisant les résultats précédents, déduire

une construction, en vraie grandeur, de la longueur de l'arête [BD] du tétraèdre BACD.

3.c)ii) Terminer le patron, avec règle et compas, en laissant apparaître les traces justificatives

des constructions. Solution [Martinique, 2000]

1. Pour chacune des affirmations suivantes dire si elle est vraie ou fausse. Argumenter la réponse. 1.a) Tous les rectangles appartiennent à (F).

1.b) Certains éléments de (F) sont des parallélogrammes. 1.a) est FAUX. En général, un rectangle n'a pas ses diagonales perpendiculaires. Lorsque les

diagonales sont perpendiculaires, le rectangle est alors un carré. 1.b) est VRAI. Le losange est un parallélogramme qui possède des diagonales perpendiculaires. 2.a) Quelle est la nature du quadrilatère EFGH ? Le démontrer. 2.b) Quelle est la condition supplémentaire à imposer à ABCD pour que EFGH soit un carré ? Le

justifier. Je commence par tracer la figure. EFGH est le parallélogramme de Varignon du quadrilatère ABCD (voir exercice : le

parallélogramme de Varignon). Ainsi, EFGH est un rectangle. Si, de plus, les diagonales de ABCD sont de même mesure, EFGH est un carré.

3.a) Construire à la règle et au compas, le quadrilatère ABCD.

Je trace un segment [AC] tel que AC = 10 cm ; je place le point I, milieu du segment [AC], donc le point I tel que AI = IC = 5 cm ; soit C1 le cercle de centre A et de rayon 6 cm et soit C2 le cercle de centre I et de rayon 5 cm ; soit B l'un des points de concours des cercles C1 et C2 (l'angleABCintercepte le diamètre [AC] et

est, par conséquent, droit) et soit B' l'autre ; je trace la droite (BB') qui est perpendiculaire à la droite (AC) (en effet, (AC) est la médiatrice du

segment [BB'] car AB = AB' et IB = IB') ; je place le point D sur la droite (BB') de telle façon que les points D et B soient de part et d'autre de

la droite (AC) et que BD = 10 cm ; je trace le quadrilatère ABCD.

Je propose la figure ... 3.b) Si O est le point d'intersection des diagonales [AC] et [BD], calculer BC puis BO.

Par application du théorème de Pythagore dans le triangle ABC rectangle en B, je trouve AC2 = AB2

Pour trouver OB, je calcule de deux manières l'aire du triangle ABC : Aire(ABC) = (BA x BC)/2 = (AC x OB)/2 pour déduire que OB = (BA x BC)/AC = (6 x 8)/10 cm = 4,8 cm.

3.c)i) Montrer que le triangle BOD est rectangle. En utilisant les résultats précédents, déduire une

construction, en vraie grandeur, de la longueur de l'arête [BD] du tétraèdre BACD.

L'énoncé nous dit que [OB] est hauteur du tétraèdre BADC, ce qui implique que la droite (OB) est

orthogonale à toute droite du plan (ACD). En particulier, la droite (OB) est perpendiculaire à la

droite (OD) et le triangle OBD est rectangle en O.

Construction utilisant règle non graduée et compas de BD : je trace un cercle, un diamètre [MN] de ce cercle et je prends un point O sur ce cercle distinct de M

et de N (l'angleMONest alors un angle droit car il intercepte un diamètre de ce cercle) ; je place B sur la demi-droite [OM) en reportant à l'aide du compas la longueur OB depuis la figure

initiale ; je place D sur la demi-droite [ON) en reportant à l'aide du compas la longueur OD depuis la figure

initiale ; je trace le segment [BD].

3.c)ii) Terminer le patron, avec règle et compas, en laissant apparaître les traces justificatives des

constructions. Les tracés relatifs à cette question sont portés en rouge.

Exercice [Limoges, 1998] D'après Maths CM2 - Nouvelle Collection -, Thevenet, Bordas, 1996, p. 117. 16 Observe le patron A quelle figure correspond ce patron ? A un prisme ? A une pyramide ? A un cube ? 1. Comment reconnaître que la figure ci-dessus, composée de quatre triangles, ne peut pas être le

patron d'un prisme, ni celui d'un cube ? 2. On admettra qu'il s'agit d'un patron de pyramide et on considérera que ce patron est constitué à

partir d'un carré ABCD, dont les côtés mesurent 4 cm. Dire, en justifiant votre réponse, où doivent

être placés le point E sur le segment [BC] et le point F sur le segment [CD] pour qu'on ait bien

affaire à un patron de pyramide. 3. Etablir quelle est la nature précise de chacune des quatre faces de la pyramide. 4. Appelons K le sommet du solide où se rejoignent les points B, C et D du patron. On obtient ainsi

la pyramide AEFK.

4.a) Montrer que l'on peut faire coïncider la pyramide avec le coin d'un cube de côté 4 cm.

Représenter un cube en perspective cavalière et y tracer une représentation de la pyramide. 4.b) Calculer le volume de la pyramide [V = (1/3) x b x h où b désigne l'aire de la base et h

désigne la hauteur correspondante]. 5. Calculer l'aire du triangle AEF.

6. Soit H la projection orthogonale de K sur le plan (AEF). Calculer KH.

7. Montrer que dans le patron ci-dessus, les droites (AE) et (BF) sont perpendiculaires. 8. Montrer que H est l'orthocentre du triangle AEF.

Solution [Limoges, 1998]

1. Comment reconnaître que la figure ci-dessus, composée de quatre triangles, ne peut pas être le

patron d'un prisme, ni celui d'un cube ? Un prisme (à priori oblique) possède au moins une face en forme de parallélogramme, ce qui n'est

pas le cas ici. Par conséquent, ce n'est pas le patron d'un cube non plus car tout cube est un prisme. 2. Dire, en justifiant votre réponse, où doivent être placés le point E sur le segment [BC] et le point

F sur le segment [CD] pour qu'on ait bien affaire à un patron de pyramide. Pour qu'on ait bien affaire au patron d'un tétraèdre, il faut qu'on puisse faire coïncider par pliage le

segment [EB] et le segment [EC], et donc que EB = EC (i.e. E milieu du segment [BC]). De même,

il faut qu'on puisse faire coïncider par pliage le segment [FC] et le segment [FD], et donc que FC

= FD (i.e. F milieu du segment [CD]). appliqué au triangle FCE rectangle en C).

4.a) Montrer que l'on peut faire coïncider la pyramide avec le coin d'un cube de côté 4 cm.

Représenter un cube en perspective cavalière et y tracer une représentation de la pyramide. Les anglesEKF,EKAetFKAsont tous droits, on peut donc faire coïncider les faces (EKF),

(EKA) et (FKA) du tétraèdre AEFK avec les faces (LKN), (LKA) et (NKA) d'un cube ABCDKLMN où les angles la hauteur correspondante]. Aire(EFK) = (KE x KF)/2 = 2 cm2. Volume(KAFE) = (KA x Aire(EFK))/3 = 8/3 cm3 ((KA) est bien orthogonale au plan (KEF) car orthogonale aux droites (KE) et (KF)).

5. Calculer l'aire du triangle AEF.

Aire(AEF) = Aire(ABCD) - Aire(ADF) - Aire(ABE) - Aire(CEF) (d'après le découpage du carré

ABCD).

Puis, Aire(AEF) = AB x AD - (AD x DF)/2 - (AB x BE)/2 - (CE x CF)/2 = (4 x 4 - (4 x 2)/2 - (4 x 2)/2 - (2 x 2)/2) cm2 = 6 cm2.

6. Soit H la projection orthogonale de K sur le plan (AEF). Calculer KH.

Un nouveau calcul du volume du tétraèdre KAFE me permet de déduire la hauteur KH du tétraèdre. Volume(KAFE) = (KH x Aire(AEF))/3 = (KH x 6)/3 cm2 = 8/3 cm3.

Je conclus que KH = 8/6 cm = 4/3 cm.

7. Montrer que dans le patron ci-dessus, les droites (AE) et (BF) sont perpendiculaires. Soit r la rotation de centre O (centre du carré ABCD) et qui envoie A sur B, B sur C, C sur D et D

sur A (propriété concernant les isométries du carré). Alors, l'image du milieu du segment [BC], E, est le milieu du segment [CD], F.

Puis, les droites (AE) et (BF) sont perpendiculaires car r((AE)) = (BF) et puisqu'une droite et son image forment entre elles l'angle de la rotation qui est de 90°.

8. Montrer que H est l'orthocentre du triangle AEF.

Soit X l'orthocentre du triangle AEF.

Voici la figure ... Je vais tout d'abord essayer de déterminer les longueurs A'X et E'Y. Je pose donc A'X = x cm et E'Y

= y cm. Détermination de AA', EE' et FF'.

Retour sur la pyramide et le point H.

Le triangle AHK est rectangle en H. On peut donc lui appliquer le théorème de Pythagore pour

segment [EF] comme axe de symétrie et comme le triangle AEH est également isocèle admettant la

médiatrice du segment [EF] comme axe de symétrie, la droite (HA) est donc une hauteur du triangle

AEF (car la médiatrice de la base principale d'un triangle isocèle est aussi hauteur issue du sommet

le point H est l'orthocentre du triangle AEF.

Note : je pourrais expliquer aussi que lors du pliage autour de la droite (AE), le point B est toujours

inclus dans un plan orthogonal à la droite (AE) pour conclure que la droite (BK) est orthogonale à la

droite (AE) sur le patron. Etc. Mais ceci était-il un argument qui aurait convaincu le jury ? Exercice [Bordeaux, Caen, Clermont, Nantes, Orléans-Tours, Poitiers, La

Réunion, 2000] On considère une pyramide SEFG. Les points I, J, K, L et M sont les milieux respectifs de [SE],

[SG], [GF], [EF] et [EG].

1. Prouver que (IL)//(JK) et que IJKL est un parallélogramme. 2. On suppose, seulement dans cette section, que SF = EG. Quelle est la nature de IJKL ? 3. On suppose, seulement dans cette section, que (SF) est orthogonale au plan (EFG). Démontrer

que IJKL est un rectangle.

4. Quelle condition suffit-il d'imposer au triangle SEG pour que le quadrilatère SIMJ soit un losange

? 5. Quelle condition suffit-il d'imposer au triangle SEG pour que le quadrilatère SIMJ soit un

rectangle ? 6. Dessiner le patron d'une pyramide SEFG telle que SIMJ soit un carré et IJKL un rectangle. Solution [Bordeaux, Caen, Clermont, Nantes, Orléans-Tours, Poitiers, La

Réunion, 2000]

1. Prouver que (IL)//(JK) et que IJKL est un parallélogramme. Je trace d'abord la figure ... Le théorème de la droite des milieux appliqué dans le triangle SEG avec I milieu du segment [SE]

et J milieu du segment [SG] donne (IJ)//(EG) et IJ = EG/2.

Le théorème de la droite des milieux appliqué dans le triangle FEG avec L milieu du segment [FE]

et K milieu du segment [FG] donne (LK)//(EG) et LK = EG/2. Ainsi (IJ)//(EG)//(LK) et les droites (IJ) et (LK) sont parallèles.

De plus, IJ = EG/2 = LK et IJ = LK.

Le quadrilatère (convexe) IJKL a ses côtés opposés [IJ] et [LK] égaux (en mesure) et parallèles, est,

par conséquent un parallélogramme.

2. On suppose, seulement dans cette question, que SF = EG. Quelle est la nature de IJKL ? De la même manière que pour la question 1, je sais que (IL)//(SF)//(JK) et que IL = SF/2 = JK.

Ainsi, si SF = EG, je déduis que IL = SF/2 = EG/2 = IJ.

Le parallélogramme IJKL possède donc deux côtés consécutifs [IJ] et [IL] égaux (en mesure) et

IJKL est un losange.

3. On suppose, seulement dans cette section, que (SF) est orthogonale au plan (EFG). Démontrer

que IJKL est un rectangle. Je sais que (SF) ┴ (EFG), mais je sais également que (IL)//(SF). Je déduis alors que (IL) ┴ (EFG).

Puis, que la droite (IL) est orthogonale à toute droite du plan (EFG) et en particulier à la droite

(LK).

Le parallélogramme IJKL possède donc deux côtés consécutifs [IL] et [LK] perpendiculaires et

IJKL est un rectangle.

4. Quelle condition suffit-il d'imposer au triangle SEG pour que le quadrilatère SIMJ soit un losange

? Le théorème de la droite des milieux appliqué dans le triangle SEG avec I milieu du segment [SE]

et M milieu du segment [EG] donne (IM)//(SG) et IM = SG/2. Or J est milieu du segment [SF], donc SJ = SG/2.

Le quadrilatère (convexe) SIMJ a ses côtés opposés [IM] et [SJ] égaux (en mesure) et parallèles,

est, par conséquent un parallélogramme.

Pour que le parallélogramme SIMJ soit un losange, il suffit qu'il ait deux côtés consécutifs égaux

(en mesure), par exemple SI = SJ (i.e. SE = SF car SI = SE/2 = SF/2 = SJ).

Sous la condition "le triangle SEF est isocèle en S", le quadrilatère IJKL est donc un losange.

5. Quelle condition suffit-il d'imposer au triangle SEG pour que le quadrilatère SIMJ soit un

rectangle ?Pour que le parallélogramme SIMJ soit un losange, il suffit qu'il ait deux côtés consécutifs

perpendiculaire, par exemple (SI) ┴ (SJ) (i.e. (SE) ┴ (SF)).

Sous la condition "le triangle SEF est rectangle en S", le quadrilatère IJKL est donc un rectangle.

6. Dessiner le patron d'une pyramide SEFG telle que SIMJ soit un carré et IJKL un rectangle. Si le triangle SEG est isocèle rectangle en S, le quadrilatère SIMJ est à la fois losange (question 4) et

rectangle (question 5), donc un carré. Si (SF) est orthogonale au plan (EFG), alors le quadrilatère IJKL est un rectangle (question 3). Ainsi, il s'agit ici de tenir compte de ces deux conditions : SFE et SFG sont deux triangles rectangles en F (ils sont isométriques), EFG est un triangle isocèle en F,

SEG est un triangle isocèle rectangle en S.

Je peux obtenir plusieurs tétraèdres différents. En effet, le point F peut se déplacer sur le demi-cercle de diamètre [SE] extérieur au trianggle EGS (cependant sans trop se rapprocher du point E)...EG

S F1F2 F3

Exercice [Lyon, 1998] On dispose d'un parallélipipède rectangle dont les côtés ont pour longueurs respectives AB = a, AD

= AA' = a/2. Soient I, J, I' et J' les milieux respectifs des segments [AB], [AD], [A'B'] et [A'D']. On considère le solide S de sommets B, D, J, I, B', D', J' et I'.

On admettra que les quadrilatères BDD'B' et IJJ'I' sont des rectangles. Dans les constructions demandées ci-dessous, on prendra pour longueur a, le segment ci-dessous : 1. Construire le quadrilatère BDJI à la règle non graduée et au compas. Indiquer sa nature. Calculer

son aire en fonction de a.

2. Construire un patron du solide S, à la règle graduée et au compas. Ecrire le programme de

construction. 3. Quelle est l'aire totale de ce solide exprimée en fonction de a ? 4. Quelle proportion du volume du parallélépipède initial représente le volume de ce solide S ? Solution [Lyon, 1998]

Je commence par tracer le solide BDJIB'D'J'I' en perspective cavalière.

1. Construire le quadrilatère BDJI à la règle non graduée et au compas. Indiquer sa nature. Calculer

son aire en fonction de a.

Dans l'ordre et en bref l'explication de la construction de la figure ... a) construction du segment [AB] de longueur a ; b) construction du milieu I du segment [AB] (construction de la médiatrice (M1M2) du

segment [AB]) ; c) construction de la perpendiculaire à la droite (AB) passant par A (construction du

symétrique I' de I par rapport au point A, puis construction de la médiatrice (N1N2) du

segment [II']) ; d) construction du point D ; e) construction du milieu J du segment [AD] (construction de la médiatrice (N1N2) du

segment [AD]) ; f) construction du point O, centre du carré (comme intersection des médianes [M1M2] et

[N1N2]) ; g) construction du symétrique C de A par rapport au point O. Les étapes f) et g) sont inutiles pour l'obtention du quadrilatère BDJI.

Pour montrer que le quadrilatère BDJI est un trapèze, il suffit d'utiliser le théorème de la droite des

milieux dans le triangle ABD où I est milieu du segment [AB] et où J est milieu du segment [AD]

pour obtenir (IJ)//(BD). Calcul de l'aire du trapèze BDJI : Aire(BDJI) = Aire(BAD) - Aire(IAJ) = (AB x AD)/2 - (AI x AJ)/2 = (3 x a2)/16.

2. Proposer un patron du solide S.

3. Quelle est l'aire totale de ce solide exprimée en fonction de a ? Il s'agit donc de l'aire du patron proposé. Aire totale = Aire(IBB'I') + Aire(BDD'B') + Aire(DJJ'D') + Aire(JII'J') + Aire(BDJI) +

Aire(B'D'J'I').

Le théorème de la droite des milieux dans le triangle ABD où I est milieu du segment [AB] et où J

Retour sur la calcul d'aire (avec toutes les conditions admises sur certaines faces, il s'agit bien d'un

4. Quelle proportion du volume du parallélépipède initial représente le volume de ce solide S ? Volume(BDJIB'D'J'I') = Aire(BDJI) x BB' = (3 x a2/16) x a/2 = 3 x a3/32.

Volume(ABCDA'B'C'D') = Aire(ABCD) x BB' = AB x AC x BB' = a3/4. Le rapport des volumes se calcule aisément : Volume(BDJIB'D'J'I')/Volume(ABCDA'B'C'D') = (3 x a3/32)/(a3/4) = 3/8. Exercice [Bordeaux, Clermont, Nantes, Poitiers, Ile de la Réunion (2), 1999]

Reproduire sur votre copie le tableau ci-dessous et le compléter en répondant par oui ou par non.

Pour la dernière ligne, on nommera un triangle autre que ceux qui figurent dans le tableau.Justifier vos affirmations concernant la nature des triangles AFC et EHG.

2. On considère que la figure ci-dessus représente un cube en bois (de 10 cm d'arête). On le partage en deux morceaux à l'aide d'une scie, qu'on suppose sans épaisseur réalisant une

coupe plane passant par les trois points R, S et T.

Le point R est à 6 cm du sommet E, sur l'arête [EH]. Le point S est à 3 cm du sommet E, sur l'arête

[EA]. Le point T est à 6 cm du sommet E, sur l'arête [EF]. On applique une des deux surfaces obtenues sur un tampon encreur et on imprime cette section RST

sur une feuille. 2.a) Sans faire de calcul, dessiner en taille réelle à l'aide de la règle et du compas le contour de la

surface imprimée. On utilisera des constructions géométriques annexes (les faire figurer sur la

copie). Expliquer succinctement la construction géométrique. 2.b) Calculer la dimension exacte de la longueur TR.

2.c) Calculer l'aire exacte en cm2 de la section obtenue. Solution [Bordeaux, Clermont, Nantes, Poitiers, Ile de la Réunion (2), 1999]

1. Reproduire sur votre copie le tableau ci-dessous et le compléter en répondant par oui ou par non.

Pour la dernière ligne, on nommera un triangle autre que ceux qui figurent dans le tableau. Il ne semble utile de justifier les réponses. Aussi, je me contente de remplir le tableau. Justifier vos affirmations concernant la nature des triangles AFC et EHG.

Le triangle EHG est isocèle rectangle en H (car EFGH est un carré). Le triangle AFC est équilatéral (en effet, si a est le côté du cube, d'après le théorème de Pythagore

non rectangle. 2.a) Sans faire de calcul, dessiner en taille réelle à l'aide de la règle et du compas le contour de la

surface imprimée. On utilisera des constructions géométriques annexes (les faire figurer sur la

copie). Expliquer succinctement la construction géométrique. Le triangleEst-il rectangle ?Est-il isocèle ?Est-il équilatéral ?

DJH ACG AFC EHG

OuiNonNon

Le triangleEst-il rectangle ?Est-il isocèle ?Est-il équilatéral ?

DJHNonOuiNon

ACGOuiNonNon

AFCNonOuiOui

EHGOuiOuiNon

OuiNonNonACJ ou ...

Je pense à tracer les triangles ERS, EST et ERT pour construire les longueurs RS, ST et RT.

Je construis un segment [R1T] qui mesure 12 cm. Je construis la médiatrice (d) du segment [R1T] (à l'aide de la règle non graduée et du compas) qui

coupe le segment [R1T] en le point E (tel que R1E = ET = 6 cm). Sur la droite (d), je place les points S et R2 tels que le point E appartienne au segment [R2S], que

R2E = 6 cm et que ES = 3 cm. Je trace le cercle C1 de centre S et de rayon [SR1] et le cercle C2 de centre T et de rayon [TR2]. Ces

cercles C1 et C2 se coupent en deux points dont l'un que je nomme R.

2.b) Calculer la dimension exacte de la longueur TR.

2.c) Calculer l'aire exacte en cm2 de la section obtenue. De la même manière, le théorème de Pythagore appliqué dans le triangle TES rectangle en E donne

TRS est isocèle en S). Le théorème de Pythagore appliqué dans le triangle SHT rectangle en H

Exercice [Besançon, 1998] ABCDEFGH est un prisme droit de "hauteur" AE = 5 cm. Les faces ABCD et EFGH sont des

trapèzes rectangles isométriques avec AD = AB = 6 cm, BC = 12 cm etDAB=ABC= 90

degrés. On place sur l'arête [DA], le point I tel que DI = 2 cm et sur l'arête [DC], le point I tel que

DJ = DC/3.

1. Calculer DC.

2. Calculer la longueur de chacune des arêtes de la pyramide DIJH.

3. Construire au compas et à la règle (règle graduée et non graduée) le triangle IJH en vraie

grandeur en laissant apparents les traits de construction. 4. Calculer l'aire du triangle ACD. En déduire celle du triangle IJD.

5. Quel est le volume du solide DIJH ? Solution [Besançon, 1998]

1. Calculer DC.

Soit H1 le pied de la hauteur du triangle BCD issue de D.

Le quadrilatère ABH1D est alors un rectangle car il possède trois angles droits (en A, en B et en H1).

2. Calculer la longueur de chacune des arêtes de la pyramide DIJH.

Les six arêtes de la pyramide DIJH sont [DI], [DJ], [DH], [IJ], [IH] et [JH].quotesdbs_dbs29.pdfusesText_35

[PDF] toute les sections d un cube

[PDF] section d'un cube par un plan seconde

[PDF] comment avoir une forte personnalité homme pdf

[PDF] comment tracer un angle de 20 sans rapporteur

[PDF] tracer un angle de 40° sans rapporteur

[PDF] angle 150°

[PDF] les barrages en terre

[PDF] barrage en terre définition

[PDF] conception d'un barrage en terre

[PDF] realisation des barrage en terre

[PDF] stabilité des barrages en terre

[PDF] résine polyester contreplaqué

[PDF] resine epoxy pour bateau

[PDF] construction bateau cp epoxy

[PDF] résine epoxy pour bois