 HOMOTHÉTIE ET AUTRES TRANSFORMATIONS
HOMOTHÉTIE ET AUTRES TRANSFORMATIONS
ET AUTRES TRANSFORMATIONS. Vidéo https://youtu.be/OVxRkeu8gTc. I. Rappels : Symétries translation et www.maths-et-tiques.fr/index.php/mentions-legales.
 TRANSFORMATIONS
TRANSFORMATIONS
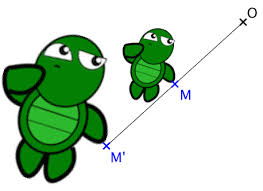
c) La tortue T1 est l'image de la tortue T4 par l'homothétie de centre O et de rapport -05. www.maths-et-tiques.fr/index.php/mentions-legales.
 Partie 1 : Agrandissement réduction
Partie 1 : Agrandissement réduction
https://www.maths-et-tiques.fr/telech/19Transfo2.pdf
 TRANSLATION ET VECTEURS
TRANSLATION ET VECTEURS
http://www.maths-et-tiques.fr/telech/Act_vect.pdf. TP info : Bonhommes et dromadaires : http://www.maths-et-tiques.fr/telech/bonhom.pdf http://www.maths-et
 NOMBRES COMPLEXES – Chapitre 2/2
NOMBRES COMPLEXES – Chapitre 2/2
Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. 4. Partie 2 : Expression complexe des transformations - ( ) = (1 − )(1 + ) . = (1 − ) ...
 LES VECTEURS
LES VECTEURS
D. C. F. E. A. D. B. C. Page 5. 5 sur 19. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. Définition : Deux vecteurs sont opposés lorsqu'ils ont
 Les similitudes
Les similitudes
7 févr. 2011 Exemple : La translation la rotation
 MODIFICATIONS DE PROGRAMME RENTRÉE 2016 – Niveau 6e
MODIFICATIONS DE PROGRAMME RENTRÉE 2016 – Niveau 6e
Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. MODIFICATIONS Transformations. - Translations. - Rotations. Pyramides et cônes. Page 4. Yvan ...
 Transformations du plan et de lespace
Transformations du plan et de lespace
L'homothétie de centre Ω et de rapport k est la transformation du Les translations autres que Id
 Transformations géométriques
Transformations géométriques
vecteur de notre translation. Il est également utile de savoir quand on peut introduire une homothétie qui envoie un certain objet sur un autre : Proposition
 [PDF] HOMOTHÉTIE ET AUTRES TRANSFORMATIONS - maths et tiques
[PDF] HOMOTHÉTIE ET AUTRES TRANSFORMATIONS - maths et tiques
Construire l'image du triangle ABC par l'homothétie de centre O et de rapport -2 On construit respectivement les symétriques A' B' et C' de A B et C par l'
 [PDF] TRANSFORMATIONS (Partie 2) - maths et tiques
[PDF] TRANSFORMATIONS (Partie 2) - maths et tiques
- L'image B' de B se trouve de l'autre côté de B par rapport au point O - OB' = 05 x OB Méthode : Construire l'image d'une figure par une homothétie
 [PDF] Transformations géométriques
[PDF] Transformations géométriques
vecteur de notre translation Il est également utile de savoir quand on peut introduire une homothétie qui envoie un certain objet sur un autre : Proposition
 [PDF] Travail de mathématiques 3èmes du 30/03/2020
[PDF] Travail de mathématiques 3èmes du 30/03/2020
30 mar 2020 · V – Homothéties : 1) Introduction et rappels : ? Une transformation du plan transforme un objet géométrique de départ (un point un segment un
 [PDF] INTRODUCTION A UNE APPROCHE HISTORIQUE
[PDF] INTRODUCTION A UNE APPROCHE HISTORIQUE
Le rôle des transformations dans la créa- tir d'autres : un cercle donnait une ellipse ou une l'homothétie feront leur apparition dans le pro-
 [PDF] introduction-aux-fonctionspdf - Zeste de Savoir
[PDF] introduction-aux-fonctionspdf - Zeste de Savoir
12 août 2019 · Vous trouvez que les maths ça ne bouge pas assez? abstraites qui transforment des objets mathématiques en d'autres objets
 [PDF] TRANSFORMATIONS DE L ESPACE EN TERMINALE C
[PDF] TRANSFORMATIONS DE L ESPACE EN TERMINALE C
1 2 TRANSLATIONS ET HOMOTHETIES Autres propriétes P1) Tout homothétie de l'espace conserve : le parallélisme l'orthogonalité les angles orien-
 [PDF] Cours de Géométrie I semestre de printemps
[PDF] Cours de Géométrie I semestre de printemps
En géométrie projective il s'agit de l'action du groupe des transformations projectives PGL(3R) sur le plan projectif P2 D'autres exemples naturels en
 [PDF] Article Chemins homothétiques
[PDF] Article Chemins homothétiques
transformation affine ayant un centre homothétique A et un rapport ? ? R qui associe tout tique Cette définition implique que
 [PDF] Semaine 8 : Homothétie etc - virginie-zampa - Free
[PDF] Semaine 8 : Homothétie etc - virginie-zampa - Free
Métiers de l'enseignement et de la formation : Math OM' = 05 x OM Deux figures homothétiques sont une réduction ou un agrandissement l'une de l'autre
![[PDF] Cours de Géométrie I semestre de printemps [PDF] Cours de Géométrie I semestre de printemps](https://pdfprof.com/Listes/16/37213-16GeometrieI.pdf.pdf.jpg)
Géométrie I
David Cimasoni
Table des matières
I Groupes et actions de groupes 5
I.1 Groupes et sous-groupes . . . . . . . . . . . . . . . . . . . . . . . . . 5 I.1.1 Groupes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 I.1.2 Sous-groupes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 I.2 Homomorphismes de groupes . . . . . . . . . . . . . . . . . . . . . . . 12 I.2.1 Homomorphismes . . . . . . . . . . . . . . . . . . . . . . . . . 13 I.2.2 Isomorphismes . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 I.3 Actions de groupes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 I.3.1 Actions de groupes, définition et exemples . . . . . . . . . . 16 I.3.2 Relations d"équivalence et orbites . . . . . . . . . . . . . . . . 17 I.3.3 Le stabilisateur . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 I.3.4 La formule des orbites . . . . . . . . . . . . . . . . . . . . . . 20 I.3.5 La formule de Burnside . . . . . . . . . . . . . . . . . . . . . . 22II Groupes d"isométries 25
II.1 Distances et isométries . . . . . . . . . . . . . . . . . . . . . . . . . . 25II.1.1 Espaces métriques . . . . . . . . . . . . . . . . . . . . . . . . . 25
II.1.2 Le groupe d"isométries d"un espace métrique . . . . . . . . . 27
II.2 Le groupe des isométries de l"espaceRn. . . . . . . . . . . . . . . .2 8 II.2.1 Le produit semi-direct . . . . . . . . . . . . . . . . . . . . . . 29
II.2.2 Applications affines . . . . . . . . . . . . . . . . . . . . . . . . 30
II.2.3 Le groupeIsom(Rn). . . . . . . . . . . . . . . . . . . . . . .3 2 II.3 Classification des isométries . . . . . . . . . . . . . . . . . . . . . . . 34
II.3.1 Le cas de la droite . . . . . . . . . . . . . . . . . . . . . . . . . 34
II.3.2 Classification des isométries du plan . . . . . . . . . . . . . . 35
II.3.3 Le cas général de l"espaceRn. . . . . . . . . . . . . . . . . .39 II.4 Groupes de symétries . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
II.4.1 Calcul de groupes de symétries . . . . . . . . . . . . . . . . . 42
II.4.2 Sous-groupes finis deIsom(Rn). . . . . . . . . . . . . . . . .47
IIIGéométrie hyperbolique 53
III.1 Inversions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53III.1.1 Définition et premières propriétés . . . . . . . . . . . . . . . . 53
III.1.2 Une application : le porisme de Steiner . . . . . . . . . . . . 58
III.1.3 Projection stéréographique . . . . . . . . . . . . . . . . . . . . 59
1
TABLE DES MATIÈRES2
6061
III.2.2 Le birapport . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
III.3 Le disque de Poincaré . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
III.3.1 La distance hyperbolique . . . . . . . . . . . . . . . . . . . . . 66
III.3.2 Le disque de Poincaré . . . . . . . . . . . . . . . . . . . . . . . 71
III.4 Isométries hyperboliques . . . . . . . . . . . . . . . . . . . . . . . . . 72
III.4.1 Le demi-plan de Poincaré . . . . . . . . . . . . . . . . . . . . 72
III.4.2 Le groupeIsom(H). . . . . . . . . . . . . . . . . . . . . . . .73
Introduction
En très résumé, l"essentiel de la première partie du cours a été consacrée à l"étude de lagéométrie euclidiennedans le plan, d"abord au moyen de méthodes classiques (chapitre I), puis au moyen de méthodes analytiques (chapitre II). Tentons de prendre un peu de recul pour discerner les concepts principaux de cette théorie. Clairement, le concept le plus fondamental est celui dedistance. En effet,lesnotions géométriquesétudiées en géométrie euclidienne sont précisément les
notions laissées invariantes par les transformations qui préservent les distances - ce qu"on appelle lesisométries. Par exemple, les propriétés telles que "être une droite", "être un cercle" ou "être deux points à distancexl"un de l"autre" sont des propriétés géométriques : toute isométrie envoie une droite sur une droite, un cercle sur un cercle, et deux points à distancexsur deux points à distance x. En revanche, "être une droite verticale" n"est pas une propriété géométrique, puisqu"elle n"est pas préservée par les isométries; "être une droite verticale" n"a, pour ainsi dire, pas de sens en géométrie euclidienne. Notons encore que l"ensembleGdes isométries du planX=R2n"est pas simplement un ensemble, mais est muni d"une structure supplémentaire. En effet, on peut toujours composer deux isométries, et le résultat sera à son tour une isométrie. De plus, l"application identité est clairement une isométrie. Finalement, l"inverse d"une isométrie est encore une isométrie. Techniquement, on dit queG est ungroupe, quiagitsur l"ensembleX. (Voir le chapitre I ci-dessous.)En résumé :
On peut comprendre la géométrie euclidienne comme l"étude des pro- priétés d"objets de l"ensembleX=R2(et plus généralement, deX=Rn)invariantes par l"action du groupeGdes isométries deX.Par la suite, nous avons brièvement traité degéométrie projective(chapitre III).
Dans cette théorie, les notions fondamentales sont celles d"alignement(de points) et deconcourance(de droites). Les transformations qui préservent ces notions sont ce qu"on appelle lestransformations projectivesdu plan projectifP2, et plus généralement de l"espace projectifPn. Ces transformations forment à leur tour un groupe, considérablement plus grand que celui des isométries euclidiennes. En géométrie projective, les notions géométriques sont les propriétés invariantes par ce groupe de transformations. Et comme ce groupe est énorme, le nombre de no- tions géométriques sera plus restreint. Par exemple, les propriétés telles que "être 3TABLE DES MATIÈRES4
une droite", "être trois points alignés" ou "être quatre points alignés de birapport xfixé" sont invariantes : ce sont des notions de géométrie projective. En revanche, les concepts tels que "distance", "cercle" et "angle" ne sont pas invariants : ils n"ont pas de sens en géométrie projective. De plus, puisqu"un énoncé de géométrie projective ne contient que des notions invariantes par le groupe des transformations projectives, il est parfois possible d"utiliser ces transformations pour ramener un tel énoncé donné en un énoncé plus simple. C"est leprincipe de Poncelet, que l"on a vu en première partie du cours, puis utilisé pour donner des démonstrations très simples des théorèmes dePappus et de Desargues.
On peut résumer cette discussion par l"affirmation suivante, à la base du programme d"Erlangenque le jeuneFelix Kleindéveloppa en 1872 : Unegéométrie, ce n"est rien d"autre qu"un groupeGagissant sur unensembleX; on étudie les propriétés invariantes par cette action.Par exemple, en géométrie euclidienne de dimension 2, on étudie les propriétés
invariantes par l"action du groupe d"isométriesG=Isom(R2)sur le planX= R2. En géométrie projective, il s"agit de l"action du groupe des transformations
projectivesPGL(3;R)sur le plan projectifP2. D"autres exemples naturels en dimension 2 sont fournis par lagéométrie hyperbolique, qui traite de l"action du groupePSL(2;R)sur le plan hyperboliqueH2, et lagéométrie sphérique, où l"on s"intéresse à l"action du groupe orthogonalO(3)sur la sphèreS2. Chacune de ces géométries a bien entendu son intérêt et son utilité propre. Notons pour finir qu"une grande partie du cours de Géométrie II sera dé- dié à l"étude d"une autre géométrie, appelée latopologie. Dans cette théorie, l"ensembleXest n"importe quel ensemble sur lequel on peut définir la notion d"application continue (ce qu"on appelle unespace topologique), et le groupeG est formé de toutes les applications bijectives continues d"inverse continue (ce qu"on appelle unhoméomorphismedeX). La topologie consiste en l"étude des propriétés des espaces topologiques invariantes par homéomorphisme : connexité, compacité, et autres. Mais ceci est une autre histoire. La seconde partie du cours de Géométrie I aura le plan suivant, que l"on espère avoir suffisamment motivé par la discussion ci-dessus. Dans un premier chapitre, nous traiterons de la théorie des groupes et des actions de groupes. Le deuxième chapitre sera consacré à l"étude du groupe des isométries euclidiennes du planR2, et plus généralement de l"espaceRn. Au chapitre trois, on donnera une introduction à la géométrie hyperbolique en dimension2, traitée avec un minimum de méthodes analytiques.Chapitre I:Groupes et actions de groupes
On va réunir dans ce chapitre toutes les considérations abstraites nécessaires au développement de la théorie. Les sections I.1 et I.2 consistent en une intro- duction standard aux concepts de groupes et d"homomorphismes de groupes. Ils seront traités de manière quelque peu aride, mais plus de détails sont donnés au cours d"Algèbre I. La section I.3 est consacrée aux actions de groupes, notion fondamentale en géométrie comme nous l"avons vu en introduction. I.1Group eset sous-group es
I.1.1Group es
Commençons par la définition d"une structure omniprésente en mathéma- tiques, celle de groupe.Définition I.1 SoitGun ensemble muni d"uneloi de composition, c"est-à-dire d"une appli- cationG×G?→G;(g;h)?→g⋆h:
On dit queGest ungroupes"il satisfait les trois axiomes suivants : (G1)Associativité:g⋆(h⋆k)=(g⋆h)⋆kpour tousg;h;k?G. (G2)Existence d"un élément neutre: il existee?Gtel quee⋆g=g⋆e=g pour toutg?G. (G3)Existence d"un inverse: pour toutg?G, il existeg′?Gtel queg⋆g′= g ′⋆g=e. Si de plus cette loi de composition satisfait l"égalitég⋆h=h⋆gpour tousg;h?G, alorsGest ditcommutatif, ouabélien.Le cardinal deG, noté?G?, est appelé sonordre.Cette définition est bien entendu très abstraite. La meilleure manière de la
"comprendre" est de se convaincre que de tels objets se retrouvent un peu partout en mathématiques, d"où l"utilité de les étudier de manière abstraite. Mais avant de donner une liste de tels exemples, quelques remarques s"im- posent. 5CHAPITRE I. GROUPES ET ACTIONS DE GROUPES6
Remarques et notations.
1. F ormellement,un group eest la donn éed"un couple (G;⋆), mais on le note simplementGlorsqu"il n"y a pas de confusion possible. On adoptera presque systématiquement la notationghau lieu deg⋆h: c"est ce qu"on appelle lanotation multiplicative. Dans le cas abélien, on utilise parfois lanotation additiveg+h. 2. L"asso ciativitésigni fieque lo rsquel"on calcule dans un group e,on p eut "laisser tomber les parenthèses". Par exemple, étant donnés quatre élé- mentsg1;:::;g4d"un groupeG, l"associativité implique les identités et l"on notera donc simplement cet élément parg1g2g3g4. Néanmoins, on conservera souvent des parenthèses, mais à des fins presque purement pédagogiques. 3. L"élémen tneut reest nécessairemen tunique. ⌜En effet, sie1ete2sont deux éléments neutres dans un groupeG, alors e1=e1⋆e2=e2;
où la première (resp. seconde) égalité découle du fait quee2(resp.e1) est unélément neutre.⌟
Cet unique élément neutre est habituellement notée, oueGen cas de confusion possible. En notation multiplicative, on le note1ou1G, d"où les égalités1g=g1=gpour toutg?G. Dans le cas abélien, en notation additive, on l"écrit0ou0G, d"où les égalités0+g=g+0=gpour toutg?G. Remarquons que l"ensemble vide n"estpasun groupe, puisqu"il ne contient pas de neutre. 4. L"in versed"un élémen tg?Gfixé est unique.⌜En effet, sig′;g′′?Gsont deux inverses deg?G, alors on a les égalités suivantes
dansG: g d"où l"identitég′=g′′.⌟ En notation multiplicative, l"unique inverse deg?Gs"écritg-1, d"où les égalitésgg-1=g-1g=1. Dans le cas abélien, en notation additive, on l"écrit-g; on écrit aussig+(-h)=?g-h, d"où l"égalitég-g=0pour toutg?G. 5. Les règles de calcul suiv antesse dé duisentdes définit ions: ?Pour tousx;g;h?G, sixg=xhougx=hx, alorsg=h.CHAPITRE I. GROUPES ET ACTIONS DE GROUPES7
?Pour tousg;h?G,(g-1)-1=get(gh)-1=h-1g-1. Dans le cas abélien, en notation additive, elles se traduisent comme suit : ?Pour tousx;g;h?G, six+g=x+halorsg=h. ?Pour tousg;h?G,-(-g)=get-(g+h)=-g-h. 6. Étan tdonné un élém entg?Get un entiern?Z, lanièmepuissance deg est l"élémentgn?Gdéfini comme suit (en notation multiplicative) : g n=⎧ ⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩g⋯g(nfois) sin>0; esin=0; g -1⋯g-1(?n?fois) sin<0: On montre facilement la troisième règle de calcul suivante : ?Pour tousg?Getn;m?Z,gngm=gn+met(gn)m=gnm. Dans le cas abélien, en notation additive, lanièmepuissance degse noten? g. Par définition, on a donc : n?g=⎧ ⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩g+⋯+g(nfois) sin>0; esin=0; (-g)+ ⋯+(-g)(?n?fois) sin<0; et la troisième règle de calcul se traduit comme suit : ?Pour tousg?Getn;m?Z,n?g+m?g=(n+m)?getm?(n?g)=(mn)?g. 7. Lorsqu"on v eutdémon trerque (G;⋆)est un groupe, il faut vérifier les axiomes(G1);(G2)et(G3), mais aussi que la loi⋆est uneloi interne, c"est à dire qu"elle définit bien une applicationG×G→G. En d"autres termes, il faut montrer g;h?G?g⋆h?G: Par exemple, l"ensembleG={-1;0;1}muni de l"addition satisfait les trois axiomes, mais n"est néanmoinspasun groupe! Voici à présent une longue liste de familles d"exemples.Exemples(de groupes).
1.Ensembles de nombres.
L"ensemble
Z={:::;-2;-1;0;1;2;:::}
des nombres entiers muni de l"addition est un groupe abélien d"ordre infini. De même, les ensemblesQ,RetCmunis de l"addition sont des groupesCHAPITRE I. GROUPES ET ACTIONS DE GROUPES8
abéliens d"ordre infini. C"est à ces exemples qu"on doit la notation additive dans un groupe abélien. Par contre, l"ensembleN={0;1;2;:::}des entiers naturels muni de l"ad- dition n"estpasun groupe : la loi est bien interne, il satisfait bien les axiomes(G1)et(G2), mais pas(G3), puisqu"aucun élément deNn"a d"inverse à l"exception du neutre. L"ensembleQ??=Q∖{0}muni de la multiplication est un groupe abélien d"ordre infini. De même, les ensemblesR??=R∖{0}etC??=C∖{0}sont des groupes abéliens (infinis) pour la multiplication, ainsi queR?+?=(0;∞).2.Espaces vectoriels.
Si(E;+;?)est un espace vectoriel surK=RouC, alors(E;+)est un groupe abélien : c"est exactement la signification des premiers quatre axiomes pour un espace vectoriel.3.Groupes de matrices.
Pourn≥1fixé etK=RouC, considérons l"ensembleGL(n;K)?={M?Mn(K) ?det(M)≠0}
des matrices carrées inversibles de taillenà coefficients dansK. Muni de la multiplication matricielle, il forme un groupe appelé legroupe général linéairede degréndeK. Notons que pourn=1, on retrouveGL(1;K)=K?=K∖{0}, qui est abélien. Le groupeGL(n;K)n"est en revanche jamais abélien pourn≥2. Similairement, on vérifie facilement que l"ensemble de matricesSL(n;K)?={M?Mn(K) ?det(M)=1}
est un groupe pour la multiplication matricielle : il s"agit dugroupe spécial linéairede degréndeK. Pourn=1, on trouveSL(1;K)={(1)}, un groupe d"ordre1. Il s"agit (d"une des "incarnations") dugroupe trivial.Pourn≥1fixé, l"ensemble
O(n)?={Q?Mn(R) ?QTQ=I}
des matrices orthogonales de taillenest un groupe pour la multiplication matricielle; on parle dugroupe orthogonalde degrén. Le théorème prin- cipal de la section II.4 (B) en première partie du cours se traduit alors comme suit : le choix d"une base orthonormale deRnpermet d"identifier les isométries linéaires deRnavec le groupeO(n).Finalement, l"ensemble
SO(n)?=SL(n;R)∩O(n)
forme un groupe, appelé legroupe spécial orthogonalde degrén. Comme ci-dessus, le choix d"une base orthonormale deRnpermet d"identifier les isométries linéaires deRnqui préservent l"orientationavec le groupe SO(n). Par des résultats vus en première partie du cours, le groupeSO(2) n"est autre que le groupe des matrices de rotation.CHAPITRE I. GROUPES ET ACTIONS DE GROUPES9
4.Cercle.
Considérons l"ensemble
S1?={z?C? ??z??=1}
des nombres complexes de norme1. Muni de la multiplication complexe, il forme un groupe abélien d"ordre infini.5.Racines de l"unité.
Soitn≥1un entier; considérons l"ensemble
n(C)?={z?C?zn=1}desracinesnièmesde l"unitédansC, illustré ci-dessous pourn=1;2;3;4.n=1n=2n=3n=4Muni de la multiplication complexe, on vérifie que c"est un groupe abélien
d"ordren. Par exemple1(C)={1}est une nouvelle incarnation du groupe trivial, tandis que2(C)={-1;1}est un groupe d"ordre2.6.Groupes symétriques.
SoitXun ensemble non-vide. Alors, l"ensemble
S(X)?={f?X→X?fest bijective}
muni de la composition des applications est un groupe : cela découle de faits élémentaires vus enLogique et théorie des ensembles. On noteraidouidXson neutre, qui est l"application identité. Ce groupe est appelé legroupe symétrique surX. SiXest un ensemble fini et que l"on numérote ses éléments{1;2;:::;n}, alors son groupe symétrique est notéSn. C"est legroupe des permutations denobjets, d"ordren!=n?(n-1)⋯2?1. Par exemple, on aS1={id}, une nouvelle incarnation du groupe trivial, etS2un groupe abélien d"ordre2, tandis queSnn"est jamais abélien pourn>2.7.Entiers modulon.
Soitn≥1un entier; considérons l"ensemble
Z n?={[0];[1];:::;[n-1]}CHAPITRE I. GROUPES ET ACTIONS DE GROUPES10
muni de la loi de composition[a]+[b]?=[`], où`?{0;1;:::;n-1}est le reste de la division dea+b?Zparn. C"est un groupe abélien d"ordren, avec élément neutre[0]et inverse-[a]=[n-a]pour touta=0;1;:::;n-1. Par exemple, la loi de composition surZ2={[0];[1]}est donnée par : [0]+[0]=[1]+[1]=[0],[0]+[1]=[1]+[0]=[1].8.Produit direct.
Soient(G1;?)et(G2;?)deux groupes. Alors, on vérifie que le produit cartésienG1×G2est un groupe pour la loi de composition suivante : pourg1;h1?G1etg2;h2?G2, on pose (g1;g2)(h1;h2)=(g1?h1;g2?h2)?G1×G2:On parle duproduit directdeG1etG2.
Plus généralement, siG1;:::;Gnsont des groupes, alors le produit carté- sienG1×???×Gnest un groupe pour la loi de composition définie compo- sante par composante. Par exemple, le groupe abélien(Rn;+)n"est autre que le produit direct dencopies de(R;+).9.Les groupes diédraux
Pourn≥2un entier fixé, notonsPnunn-gone régulier (sin=2, il s"agit d"un segment de droite). Pour fixer les idées, disons quePnest le polygone avec sommets en l"ensemblen(C)des racinesnièmesde l"unité dansC. Considérons l"ensembleD2nde toutes lessymétries dePn, c"est-à-dire les isométries du planR2=Cqui préservent globalementPn: D2n={f?R2→R2?fest une isométrie etf(Pn)=Pn}:
Muni de la composition des isométries,D2nest un groupe appelé legroupe diédral. Nous allons maintenant vérifier qu"il est d"ordre2n, d"où la notation. (C"est un premier exemple de détermination d"un groupe de symétrie; de nombreux autres exemples seront donnés en section II.4.) Plus précisé- ment, soientr?D2nl"isométrie donnée par la rotation d"angle2?ndans le sens trigonométrique autour de l"origine, ets?D2nl"isométrie donnée par la réflexion d"axe horizontal, i.e la conjugaison complexe. Nous allons vé- rifier que tout élémentdeD2ns"écrit de manière unique comme=r`s" avec`=0;1;:::;n-1et"=0;1. ⌜En effet, on verra en section II.4.1 qu"une telle isométrie doit forcément fixer l"origine. Par un résultat de la première partie du cours, c"est donc une isomé- trielinéaire. Par l"exemple 3 ci-dessus, le choix d"une base orthonormale deR2 (disons,(1;i)) permet d"identifier ces isométries avec le groupeO(2). Ainsi, on s"intéresse à l"ensemble D2n={?O(2) ?(Pn)=Pn}:
CHAPITRE I. GROUPES ET ACTIONS DE GROUPES11
Comme nous l"avons rappelé en exemple 3 ci-dessus,SO(2)est l"ensemble de matrices de rotations. Ainsi, l"intersectionD2n∩SO(2)est l"ensemble des ro- tations du plan autour de l"origine qui fixentPn, donc les rotations d"angle un multiple de2?n. En clair, D2n∩SO(2)={r`?`=0;1;:::;n-1};
soitnéléments distincts. D"autre part, considérons l"application deD2n∩SO(2) dans{?D2n??SO(2)}qui associe àsa compositionsavecs. Il s"agit clairement d"une bijection (d"inverse↦s, puisques2=1). Ainsi, {?D2n??SO(2)}={r`s?`=0;1;:::;n-1}; à nouveaunéléments distincts. CommeD2nest l"union disjointe de cet ensemble et deD2n∩SO(2), l"affirmation est démontrée.⌟ La façon dont se composent les éléments de ce groupe est entièrement déterminée par les égalités suivantes, aussi appeléesrelations: r n=1; s2=1etsr`s=r-`pour tout`: Si les deux premières relations sont claires, la troisième est moins évidente et se comprend à l"aide de la figure suivante. (Bien-sûr, une preuve formelle peut se faire à l"aide des matrices associées àrets.)s s r `r Il s"ensuit que le groupe diédral d"ordre2nn"est jamais abélien sin≥3. En effet, les relations ci-dessus impliquent les égalitéssr=r-1s=rn-1s qui n"est pas égal àrssin≥3. I.1.2Sous-group es
Passons à présent à la seconde définition de cette section.Définition I.2 SoitGun groupe, etH?Gun sous-ensemble deG. On dit queHest un sous-groupedeG, notéHP ourtous h1;h2dansH,h1h2appartient aussi àH.
CHAPITRE I. GROUPES ET ACTIONS DE GROUPES12
2.L"élémen tneut reeGappartient àH.
3. P ourtout élémen th?H, son inverseh-1appartient aussi àH. Un exercice amusant consiste à vérifier que, dans le cas d"un sous-ensembleH non-vide, ces trois propriétés sont équivalentes à une unique condition. Comme il s"agit d"un des premiers exercices de ce type, il n"est sans doute pas inutile de le résoudre ici. Lemme I.1.SoitGun groupe. Un sous-ensemble non-videH?Gest un sous- groupe deGsi et seulement si, pour toush1;h2dansH,h1h-12appartient aussiàH.
Démonstration.Les trois propriétés ci-dessus impliquent trivialement la condi- tion de l"énoncé; vérifions la réciproque. Soit doncH?Gnon-vide satisfaisant la condition de l"énoncé, que l"on notera par(C). CommeHest non-vide, il existe h?H. Par la condition(C)appliquée àh1=h2=h?H,hh-1=eappartient àH, et la seconde propriété est vérifiée. Soit à présenth?Hquelconque; par la condition(C)appliquée àh1=e(élément deHpar le point précédent) et h2=h?H,eh-1=h-1appartient aussi àH, et la troisième propriété est vérifiée.
Reste la première propriété. Soient donch1;h2?H; par la condition(C)appli- quée àh1?Heth-12(élément deHpar le point précédent),h1(h-12)-1=h1h2 appartient aussi àH, ce qui conclut la démonstration.Exemples(de sous-groupes). 1. P ourtout group eG, les sous-ensemblesH={e}etH=Gsont triviale- ment des sous-groupes deG. 2. Clairemen t,les en tiersfo rmentun sous-gr oupedes rationnels : Z2etZ2sont vraiment deux noms différents pour "le même groupe". Comment
traduire cette intuition en un énoncé plus précis? Voici un principe assez général en mathématiques1: après avoir muni un
ensemble d"une structure (par exemple, celle d"espace vectoriel), il est utile de1. Ce principe est formalisé dans ce qu"on appelle lelangage des catégories.
CHAPITRE I. GROUPES ET ACTIONS DE GROUPES13
considérer les applications qui préservent cette structure (dans cet exemple, les applications linéaires). Cela permet en particulier de répondre à la question ci- dessus. Pour la structure de groupe, ce rôle est joué par ce qu"on appelle leshomo- morphismes de groupes. I.2.1quotesdbs_dbs29.pdfusesText_35[PDF] imparfait ou passé simple - Le Baobab Bleu
[PDF] Exercices conjugaison imparfait et passé simple
[PDF] Mesures et incertitudes en Terminale S - Sciences Physiques ac
[PDF] Naviguer sur Internet - coursdinfo
[PDF] Réunion et intersection d 'intervalles - Parfenoff
[PDF] Isométries vectorielles
[PDF] TD 7 IJA Les interfaces graphiques JAVA
[PDF] COMPRÉHENSION FINE
[PDF] lecture de consignes - Académie de Nancy-Metz
[PDF] lecture de consignes - Académie de Nancy-Metz
[PDF] Lecture de consignespdf
[PDF] La vie au Moyen-âge
[PDF] Exercices d 'entrainement pour le chapitre 03 (limites et continuité)
[PDF] Fonction logarithme népérien
