 Résolution numérique déquations différentielles
Résolution numérique déquations différentielles
6 mars 2018 Cela semble indiquer que la méthode d'Euler est une méthode d'ordre 1. ... 3 Et avec Python ? Il faut utiliser la fonction odeint de Python de la ...
 Informatique en CPGE (2018-2019) Résolution numérique d
Informatique en CPGE (2018-2019) Résolution numérique d
26 mars 2019. S. B.. Présentation en Latex avec Beamer. Page 2. Méthode d'Euler. Exemples. Complément. Les équations différentielles permettent de modéliser
 Résolution numérique déquations différentielles
Résolution numérique déquations différentielles
Ou bien définie par morceaux avec de telles fonctions. 2.2 Schéma d'intégration d'Euler explicite. Un schéma d'intégration est une méthode qui calcule
 Méthode dEuler 1er ordre
Méthode dEuler 1er ordre
d'une équation différentielle du 1er ordre de la forme: y (t) = f (t
 Informatique en PCSI et MPSI Champollion 2013-2014 Méthodes d
Informatique en PCSI et MPSI Champollion 2013-2014 Méthodes d
19 févr. 2014 Implémentation de la méthode d'Euler en Python. A. Hassan@Champollion ... Équation différentielle autonome(stationnaire) : f ne dépend pas de t ...
 Résolution numérique dune équation différentielle
Résolution numérique dune équation différentielle
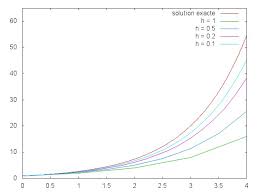
Elle fournit un résultat visuellement un peu meilleur que la méthode d'Euler classique mais s'éloigne elle aussi de la solution exacte : page 2. Page 3. x4
 Intégration numérique déquations différentielles
Intégration numérique déquations différentielles
Intégration numérique d'équations différentielles – p. 6. Page 7. Stabilité. De l'autre côté la méthode d'Euler donne pour l'équation pour la dynamique de.
 Physique-chimie
Physique-chimie
L'étude de la charge d'un condensateur permet de mettre en place une résolution d'équation différentielle fondée sur la méthode d'Euler et de comparer les
 Méthode dEuler vectorielle
Méthode dEuler vectorielle
Écrire en Python la méthode d'Euler pour t ∈ [05]
 Analyse numérique avec Python
Analyse numérique avec Python
22 mai 2014 parlent effectivement d'intégrer une équation différentielle plutôt que ... Programme Python pour la méthode d'Euler à deux fonctions inconnues :.
 Résolution numérique déquations différentielles
Résolution numérique déquations différentielles
6 ???. 2018 ?. C'est une équation différentielle d'ordre 1 mais elle n'est pas linéaire. ... Cela semble indiquer que la méthode d'Euler est une méthode ...
 Informatique en PCSI et MPSI Champollion 2013-2014 Méthodes d
Informatique en PCSI et MPSI Champollion 2013-2014 Méthodes d
19 ????. 2014 ?. Résolution des équation différentielles ordinaires (EDO) ... Implémentation de la méthode d'Euler en. Python. Runge Kutta d'ordre 4.
 Résolution numérique déquations différentielles
Résolution numérique déquations différentielles
Ou bien définie par morceaux avec de telles fonctions. 2.2 Schéma d'intégration d'Euler explicite. Un schéma d'intégration est une méthode qui calcule
 Analyse numérique avec Python
Analyse numérique avec Python
22 ??? 2014 ?. des équations différentielles) en ne cherchant surtout pas à comprendre les mathématiques ... Programme Python pour la méthode d'Euler :.
 Informatique en CPGE (2018-2019) Résolution numérique d
Informatique en CPGE (2018-2019) Résolution numérique d
26 mars 2019. S. B.. Présentation en Latex avec Beamer. Page 2. Méthode d'Euler. Exemples. Complément. Les équations différentielles permettent de modéliser
 Résolution numérique dune équation différentielle
Résolution numérique dune équation différentielle
équation différentielle. Exercice 1. plt.plot(t x1
 Méthode dEuler 1er ordre
Méthode dEuler 1er ordre
Exemple d'équation différentielle non linéaire. Écrire en Python la méthode d'Euler sur [?22]
 TP Informatique no 8/9 Équations différentielles
TP Informatique no 8/9 Équations différentielles
? Adapter la méthode d'Euler pour résoudre une équation du type Z/ = A ? Z. Il s'agit donc d'écrire en Python la fonction euler_ordre2(f y0
 Intégration numérique déquations différentielles
Intégration numérique déquations différentielles
Pour ? < 0 la méthode d'Euler est stable seulement pour ?t ?. 2.
 Physique-chimie
Physique-chimie
L'étude de la charge d'un condensateur permet de mettre en place une résolution d'équation différentielle fondée sur la méthode d'Euler et de comparer les
 [PDF] méthode dEuler
[PDF] méthode dEuler
26 mar 2019 · Méthode d'Euler Exemples Complément Informatique en CPGE (2018-2019) Résolution numérique d'équations différentielles: méthode d'Euler
 [PDF] Résolution numérique déquations différentielles - cpge paradise
[PDF] Résolution numérique déquations différentielles - cpge paradise
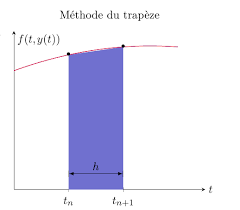
L'implémentation de la méthode d'Euler explicite est des plus simple Elle prend trois arguments : la fonction f la valeur y0 de la fonction y à l'instant t0
 [PDF] Résolution numérique déquations différentielles
[PDF] Résolution numérique déquations différentielles
6 mar 2018 · Elles consistent en général à approximer la solution y en un certain nombre de points répartis sur [t0tf ] 1 La méthode d'Euler 1 1 Le
 [PDF] Méthode dEuler - Étienne Thibierge
[PDF] Méthode dEuler - Étienne Thibierge
Mettre en œuvre la méthode d'Euler explicite afin de résoudre une équation différentielle d'ordre 1 Utiliser la fonction odeint de la bibliothèque scipy
 [PDF] Intégration des équations différentielles : méthode dEuler
[PDF] Intégration des équations différentielles : méthode dEuler
Intégration des équations différentielles : méthode d'Euler Le système différentiel est défini dans une fonction python de la forme systeme(Yt)
 [PDF] Méthode Euler - RTC
[PDF] Méthode Euler - RTC
Méthode d'Euler On considère une équation différentielle d'ordre 1 avec condition initiale (problème de Cauchy): y' = F(y t) } y(to) = Vo
 [PDF] Résolution numérique dune équation différentielle
[PDF] Résolution numérique dune équation différentielle
La fonction odeint nous permet d'obtenir une résolution numérique de référence pour l'équation différentielle qui nous intéresse : def f(x t):
 [PDF] Résolution numérique des équations différentielles
[PDF] Résolution numérique des équations différentielles
Figure 2 – Méthode d'Euler explicite avec n = 4 puis avec n = 10 notablement atténuer la divergence de la solution numérique de la solution analytique
 [PDF] Informatique en PCSI et MPSI Champollion 2013-2014 Méthodes d
[PDF] Informatique en PCSI et MPSI Champollion 2013-2014 Méthodes d
19 fév 2014 · Champollion 2013-2014 Méthodes d'Analyse Numérique Implémentation et Application en Python Équations différentielles ordinaires
 [PDF] Résolution par EULER déquations différentielles dordre 1
[PDF] Résolution par EULER déquations différentielles dordre 1
Méthode d'EULER - HEUN - RK4 - Résolution numérique d'une équation différentielle d'ordre 1 on fait simplifié écriture dans python : y(tn) ? yn
Corrigéinformatique commune
Résolution numérique d"une
équation différentielleExercice 1.On commence par importer les différents modules et fonctions dont nous auront besoin :importnumpy as np
importmatplotlib.pyplot as pltfromscipy.integrateimportodeintLa fonctionodeintnous permet d"obtenir une résolution numérique de référence pour l"équation différentielle qui nous
intéresse :deff(x, t): returnnp.sin(t)*np.sin(x) t = np.linspace(0, 50, 256) x = odeint(f, 1, t) plt.plot(t, x) plt.title( solution de x "=sin(t)sin(x)") plt.show()010203040501.01.21.41.61.82.02.22.42.62.8solution de x'=sin(t)sin(x) La méthode d"Eulerse définit ainsi :defeuler(f, x0, t): n =len(t) x = [x0] forkinrange (0, n1): h = t[k+1]t[k] p1 = f(x[k], t[k]) x.append(x[k] + h*p1)returnxmais le résultat est assez décevant, la solution fournie par la méthode s"éloigne irrémédiablement de la vraie solution :
http://info-llg.fr/page 1 x1 = euler(f, 1, t) plt.plot(t, x,"", label="Solutionexacte ") plt.plot(t, x1, label= M thode d "Euler") plt.title( M thode d "Euler") plt.legend(loc="upperleft ") plt.show()010203040501.01.52.02.53.03.5Méthode d'EulerSolution exacte
Méthode d'EulerEn revanche, les méthodes deHeunet RK4s"avèrent bien plus précises :defheun(f, x0, t):
n =len(t) x = [x0] forkinrange (0, n1): h = t[k+1]t[k] p1 = f(x[k], t[k]) p2 = f(x[k] + h*p1, t[k+1]) x.append(x[k] + h*(p1 + p2) / 2) returnxdefrk4(f, x0, t): n =len(t) x = [x0] forkinrange (0, n1): h = t[k+1]t[k] p1 = f(x[k], t[k]) p2 = f(x[k] + h*p1 / 2, t[k] + h / 2) p3 = f(x[k] + h*p2 / 2, t[k] + h / 2) p4 = f(x[k] + h*p3, t[k+1]) x.append(x[k] + h*(p1+2*p2+2*p3+p4) / 6) returnxet fournissent des résultats peu discernables de la solution exacte. Enfin, la méthode d"Eulerimplicite est définie par :fromscipy.optimizeimportnewton defeulerbis(f, x0, t): n =len(t) x = [x0] forkinrange (0, n1): h = t[k+1]t[k] s = newton(lambdau: ux[k]f(u, t[k+1])*h, x[k]) x.append(s)returnxElle fournit un résultat visuellement un peu meilleur que la méthode d"Eulerclassique, mais s"éloigne elle aussi de la
solution exacte : page 2 x4 = eulerbis(f, 1, t) plt.plot(t, x,"", label="Solutionexacte ") plt.plot(t, x4, label= M thode d "Euler") plt.title( M thode d "Eulerimplicite ") plt.legend(loc="best") plt.show()010203040500.51.01.52.02.53.0Méthode d'Euler impliciteSolution exacte
Méthode d'EulerExercice 2.On définit l"erreur de la méthode ainsi :deferreur(methode, n): t = np.linspace(0, 2, n) deff(x, t):returnx x = methode(f, 1, t) m = 0 forkinrange (n): m =max(m,abs(x[k]np.exp(t[k])))returnmLa recherche du rang minimal pour une précision donnée peut être réalisée par une méthode dichotomique, à condition
de posséder une valeurn0qui réalise cette précision (valeur qu"on peut obtenir en tâtonnant). On définit donc la fonction :defrang(methode, epsilon, n0):
iferreur(methode, n0) > epsilon: returnNone a, b = 2, n0 whileba > 1: c = (a + b) // 2 iferreur(methode, c) > epsilon: a = c else: b = c returnbCette fonction fournit les résultats suivants : >>>rang(euler, 1e1, 200) 147>>>rang(euler, 1e2, 2000) 1477
>>>rang(euler, 1e3, 20000)
14777>>>rang(heun, 1e2, 100)
32>>>rang(heun, 1e4, 1000) 315
>>>rang(heun, 1e6, 10000)
3140>>>rang(rk4, 1e4, 100)
13 >>>rang(rk4, 1e8, 200) 120>>>rang(rk4, 1e12, 1500)
1187http://info-llg.fr/page 3
Exercice 3.On obtient la solution numérique de ce système à l"aide du script :defF(X, t): [x, y] = X return[np.cos(t)*xnp.sin(t)*y, np.sin(t)*x + np.cos(t)*y] t = np.linspace(0, 4, 256)X = odeint(F, [1, 0], t)
x, y = X[:, 0], X[:, 1] plt.plot(t, x, label="x") plt.plot(t, y, label="y") plt.legend(loc="best") plt.title("Solutionexacte ") plt.grid() plt.show()0.00.51.01.52.02.53.03.54.01.0 0.50.00.51.01.52.02.53.0Solution exacte
x y La méthode d"Eulervectorielle peut se définir ainsi :defeuler_vect(F, X0, t): n =len(t)X = [X0]
forkinrange (0, n1): h = t[k+1]t[k] p1 = F(X[k], t[k])X.append([X[k][0] + h*p1[0], X[k][1] + h*p1[1]])
returnXet le graphe obtenu est très proche du graphe exact :X1 = euler_vect(F, [1, 0], t)
x1 = [z[0]forzinX1] y1 = [z[1]forzinX1] plt.plot(t, x1, label="x") plt.plot(t, y1, label="y") plt.legend(loc="best") plt.title( M thode d "Eulervectorielle ") plt.grid() plt.show()page 40.00.51.01.52.02.53.03.54.01.0
0.50.00.51.01.52.02.53.0Méthode d'Euler vectorielle
xyOn peut noter une légère différence entre les deux scripts pour définirxety; cette différence est due au fait que dans le
premier script, X est un tableaunumpyqui permet une indexation plus aisée des tableaux bi-dimensionnels.
Exercice 4.
É quationde V ander P ol
Commençons par définir la fonction qui caractérise l"équation différentielle :deff(X, t):
x, dx = X return[dx, mu*(1x*x)*dxx]On obtient ensuite les deux graphes demandés à l"aide du script : t = np.linspace(0, 30, 512) mu = 1 forvin[.001, .01, .1, 1]:X = odeint(f, [0, v], t)
plt.figure(1) plt.plot(t, X[:, 0]) plt.figure(2) plt.plot(X[:, 0], X[:, 1]) plt.figure(1) plt.title("Équationde Van der Pol ") plt.grid() plt.figure(2) plt.title("Diagrammedes phases ") plt.grid() plt.show()http://info-llg.fr/page 50510152025303
2 10123Équation de Van der Pol3
2 1 012332 1
0123Diagramme des phasesOn observent que les solutions convergent vers un régime périodique indépendant (à un déphasage près) des conditions
initiales.Nous allons maintenant constater qu"en jouant sur le paramètre, il est possible d"obtenir des solutions sensiblement non
sinusoïdales :plt.figure(3, figsize=(12,6)) t = np.linspace(0, 50, 512) formuin[1, 5, 10]:X = odeint(f, [2, 0], t)
plt.plot(t, X[:, 0], label="mu= {} ".format(mu)) plt.title("Dépendancedu param ètremu ") plt.legend(loc="lowerleft ") plt.show()010203040503 2 10123Dépendance du paramètre mu
mu = 1 mu = 5mu = 10On peut observer que le phénomène de relaxation est d"autant plus marqué queaugmente.
Par ailleurs, il apparaît que la période dépend du paramètre. Pour calculer celle-ci, on calcule la moyenne des écarts
entre deux maximums consécutifs à l"aide de la fonction : page 6 defperiode(t, x): s = [] forkinrange (1,len(t)1): ifx[k1] < x[k]andx[k+1] < x[k]: s.append(t[k]) p = 0 forkinrange (1,len(s)): p += s[k]s[k1]returnp / (len(s)1)En faisant varierentre 0 et 4 on obtient le graphe des périodes suivant :plt.figure(4)
mus = np.linspace(0, 4, 200) per = [] formuinmus: x = odeint(f, [2, 0], t) per.append(periode(t, x[:, 0])) plt.plot(mus, per) plt.title("Valeurde la p ériodeen fonction de mu ") plt.grid()plt.show()0.00.51.01.52.02.53.03.54.06.06.57.07.58.08.59.09.510.010.5Valeur de la période en fonction de muEnfin, l"excitation de cet oscillateur par un terme harmonique permet d"observer que l"amplitude de l"onde est indépen-
dante de la force extérieure appliquée, avec néanmoins un comportement chaotique.mu = 8.53A = 1.2
omega = .1 defg(X, t): x, dx = X return[dx, mu*(1x*x)*dxx + A*np.sin(2*np.pi*omega*t)] plt.figure(5, figsize=(12,4)) t = np.linspace(0, 200, 500)X = odeint(g, [2, 0], t)
plt.plot(t, X[:, 0]) plt.title("Oscillationsforc ées") plt.grid() plt.show()http://info-llg.fr/page 70501001502003
2 10123Oscillations forcées
page 8quotesdbs_dbs29.pdfusesText_35[PDF] résolution numérique des équations différentielles ordinaires exercices corrigés
[PDF] consommation marqueur social
[PDF] les differentes finalités d'une entreprise
[PDF] les finalités de l'entreprise management
[PDF] les finalités de l'entreprise cours
[PDF] les finalités de l'entreprise pdf
[PDF] les finalités de l'entreprise cours ofppt
[PDF] objectif entreprise 2016 complet
[PDF] classement des pays consommateur d'alcool en afrique 2017
[PDF] les pays qui consomment le plus d'alcool en afrique
[PDF] classement des pays consommateur d'alcool en afrique 2016
[PDF] top 10 des pays consommateur d'alcool en afrique
[PDF] le pays le plus grand consommateur de biere en afrique
[PDF] statistiques consommation alcool france 2016
