 La fonction Arctangente
La fonction Arctangente
Pour le calcul la calculatrice utilise l'algorithme CORDIC. Page 3. 5°) Valeurs remarquables. On utilise une lecture inverse du tableau des
 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Formulaire de trigonométrie 1 Fonctions trigonométriques
Formulaire de trigonométrie 1 Fonctions trigonométriques
On peut donner explicitement quelques valeurs remarquables : cos(0) = 1 arctan(x) + arctan(y) = arctan ( x + y. 1 − xy. ) + kπ o`u k = 1 si xy > 1 et x ...
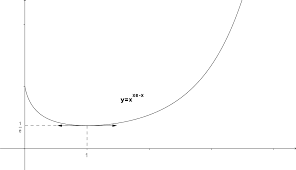 Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Valeurs remarquables de cosinus sinus et tangente. On consid`ere le nombre arctan est dérivable sur R. Il en résulte que f est la composée de deux ...
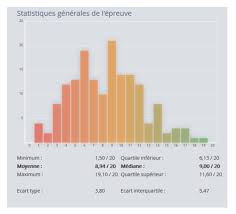 2020 Lépreuve de Calcul et Raisonnement de la session 2020 est
2020 Lépreuve de Calcul et Raisonnement de la session 2020 est
valeurs remarquables de la fonction arctan – et qu'il ne parvenait pas `a les retrouver. Ensuite viennent des calculs classiques de dérivées : `a nouveau ...
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Développements limités usuels en 0
Développements limités usuels en 0
2 Valeurs remarquables π. 6 π. 4 π. 3. 1. 2. √2. 2. √3. 2. 1. 2. 0 π. 2 π. 2. 0 tan x Arctan x + Arctan y = Arctan x + y. 1 − xy+ επ où ε = ⎧⎪⎪⎨. ⎪⎪ ...
 Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
• Valeurs remarquables : ∗ sin(0) = 0. ∗ sin (π. 6 ) = sin (5π. 6 ) = 1. 2 Arctangente f : x ↦→ Arctan(x). • Définition : Réciproque de tan sur ] − π. 2.
 Christine Nazaret
Christine Nazaret
Sinus et cosinus : valeurs remarquables remarquables on tire. Θ=arctan(b/a) [2k π]. Si a<0. On a toujours tan(θ)=b/a mais Θ≠arctan(b/a). Θ=arctan(b/a)+π [2k ...
 Feuille dexercices 7 Fonctions trigonométriques réciproques
Feuille dexercices 7 Fonctions trigonométriques réciproques
< 1 ⇒ 0 = arctan(0) < arctan (. 5. 12. ) < arctan(1) = . 4. Car arctan est remarquables. 6. Tracer le graphe de sur ℝ . Correction exercice 9. 1. Pour ...
 La fonction Arctangente
La fonction Arctangente
Pour le calcul la calculatrice utilise l'algorithme CORDIC. Page 3. 5°) Valeurs remarquables. On utilise une lecture inverse du tableau des
 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
Valeurs remarquables : ? ln(1) = 0. ? ln(e) = 1 Autres propriétés remarquables : ... ?x ? R+ Arctan(x) ? x (comparaison à la tangente en 0).
 Les-nombres-complexes.pdf
Les-nombres-complexes.pdf
la tangente: Soit z=a+ib non nul. Si a>0. Alors de tan(?)=b/a avec la calculatrice ou le tableau des valeurs remarquables
 Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Valeurs remarquables de cosinus sinus et tangente 2. f est la composée de arctan et g donnée par g(t) = sin(t). 1 ? cos(t). : f = arctan ?g.
 Ex_ sur les fonctions trigonométriques réciproques
Ex_ sur les fonctions trigonométriques réciproques
Arctan y x. . Contrôler sur la calculatrice graphique. On pourra comparer et à des valeurs remarquables de Arcsin. • Calculer.
 fonctions-usuelles.pdf
fonctions-usuelles.pdf
f(x)=arcsin(x) g(x)=arccos(x) h(x)=arctan(x)?? a) Fonctions hyperboliques f(x)=sinh(x)g(x)=cosh(x) h(x)=tanh(x)? Sinus et cosinus : valeurs remarquables.
 Les fonctions circulaires réciproques
Les fonctions circulaires réciproques
9 déc. 2020 Remarquons que la fonction Arcsin réciproque d'une bijection impaire
 Feuille dexercices 7 Fonctions trigonométriques réciproques
Feuille dexercices 7 Fonctions trigonométriques réciproques
2 arctan (. 1. 3. ) Correction exercice 2. 1. 0 <. 1. 3. < 1 ? arctan(0) < arctan (. 1. 3. ) < arctan(1). Car arctan est strictement croissante donc.
 Fonctions circulaires et applications r´eciproques
Fonctions circulaires et applications r´eciproques
Quelques valeurs remarquables des fonctions sinus cosinus et tangente Il faut prendre garde au fait que l'expression Arcsin(sin?) est définie pour tout ...
 [PDF] La fonction Arctangente
[PDF] La fonction Arctangente
On utilise une lecture inverse du tableau des valeurs remarquables Nous pouvons également obtenir les valeurs des arctangentes de (cf voir V) x 0 6
 [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
1 mar 2017 · On note arcsin : [?11] ? [??/2 ?/2] la fonction réciproque i e si valeurs intermédiaires pour tout ?1 ? y ? 1 il existe ??/2
 [PDF] Feuille dexercices 7 Fonctions trigonométriques réciproques
[PDF] Feuille dexercices 7 Fonctions trigonométriques réciproques
1 + tan2( ) = 2sin( ) cos( ) × cos2( ) = 2sin( )cos( ) = sin(2 ) 3 sin(2arctan( 1 3 )) = 2tan(arctan ( 1 3))
 [PDF] Formulaire de trigonométrie 1 Fonctions trigonométriques - LPSM
[PDF] Formulaire de trigonométrie 1 Fonctions trigonométriques - LPSM
On peut donner explicitement quelques valeurs remarquables : cos(0) = 1 ; cos (?6) = ?3 2; cos (?4) = ?2 2; cos (?3) = 1 2; cos (?2) = 0 On en déduit
 [PDF] Les fonctions de référence
[PDF] Les fonctions de référence
La fonction Arctan est impaire La démonstration de ce théorème est identique à la démonstration du théorème 14 page 21 Valeurs usuelles de la fonction
 [PDF] Chapitre bonus 1 : Trigonométrie - Julian Tugaut
[PDF] Chapitre bonus 1 : Trigonométrie - Julian Tugaut
Fonctions tangente et arctangente 4 Formules trigonométriques 5 Angles remarquables Elle est `a valeurs dans l'intervalle [?1; 1] Julian Tugaut
 Arc tangente - Vikidia lencyclopédie des 8-13 ans
Arc tangente - Vikidia lencyclopédie des 8-13 ans
Graphe de la fonction arctan La fonction arc tangente est l'application réciproque de la Valeurs remarquables[modifier modifier le wikicode]
 [PDF] Les fonctions circulaires réciproques - MPSI - Camille Guerin
[PDF] Les fonctions circulaires réciproques - MPSI - Camille Guerin
Remarquons que Arctan réciproque d'une fonction impaire est elle aussi impaire Voici quelques valeurs remarquables de la fonction Arctan x 0 ? 3 3
 [PDF] Fonctions trigonométriques réciproques
[PDF] Fonctions trigonométriques réciproques
[ arctan[tan(y)] = y 2) On a aussi : ?x?[-1 ;1] arcsin(-x) = -arcsin(x) et ?x
Comment calculer les valeurs de arctan ?
La règle de la fonction arc tangente de base est f(x)=arctan(x). f ( x ) = arctan ? On note aussi cette fonction f(x)=tan?1(x). f ( x ) = tan ? 1 ?Comment montrer que la fonction arctangente est impaire ?
tan y x = - - . Arctan x y - = - . Arctan Arctan y y - = - . Il en résulte que la fonction Arctan est impaire.Quand on utilise Arcsin ?
Les relations Arcsinus, Arccosinus et Arctangente permettent de calculer la valeur d'un angle aigu d'un triangle rectangle dont on connaît les côtés.- La valeur exacte de arctan(?1) est ??4 . Le résultat peut être affiché en différentes formes.
Chapitre II
Fonctions circulaires et applications
r´eciproquesA Fonctions circulaires
A.1 Rappels de trigonom
´etrie?Les fonctions sinus, cosinus et tangenteLes fonctionscosinusetsinussont d´efinies surR, `a valeurs dans [-1,1], 2π-p´eriodiques et d´erivables surRavec pour toutx?R cos ?x=-sinxet sin?x= cosx. Par ailleurs, la fonction cosinus est paire et la fonc- tion sinus est impaire. On appellefonction tangentela fonction not´ee tan d´efinie surR\?π2 +πZ?par tanx=sinxcosx Il s"agit d"une fonction impaire,π-p´eriodique, in- finiment d´erivable surR\?π2 +πZ?et qui v´erifie pour toutx?? -π2 ,π2 tan ?(x) =1cos2x= 1 + tan2x.x
cosx sinx tanx28Chapitre II- Fonctions circulaires et applications r´eciproques?Quelques valeurs remarquables des fonctions sinus, cosinus et tangentex0π
6π 4π 3π22π33π45π6π
sinx012⎷2
2⎷3
21⎷3
2⎷2
2120 cosx1⎷3
2⎷2
2120- 12- ⎷2 2- ⎷3
2-1tanx01⎷31⎷3-
⎷3-1-1⎷30
Beaucoup d"autres valeurs remarquables se retrouvent ais´ement `a partir de celles qui pr´ec`edent en
utilisant les relations entre sinus et cosinus.A.2 Variations de la fonction sinusPuisque la fonction sinus est 2π-p´eriodique et impaire, il suffit de connaˆıtre ses variations sur l"intervalle
[0,π] pour en d´eduire les variations surR.x0π2π sin?x= cosx1 + 0- -1 sinx1 0 0 0π 2π3π22π-π2-π-3π2-2π
-11 | | | |||||y= sinxA.3 Variations de la fonction cosinusLa fonction cosinus est 2π-p´eriodique et paire, il suffit donc de connaˆıtre ses variations sur l"intervalle
[0,π] pour en d´eduire les variations surR. x0π2π cos?x=-sinx0- -1-0 cosx 1 -1 0A- Fonctions circulaires290π
2π3π22π-π2-π-3π2-2π
-11 | | | |||||y= cosxA.4 Variations de la fonction tangenteLa fonction tangente estπ-p´eriodique et impaire donc il suffit donc de connaˆıtre ses variations sur
l"intervalle?0,π2 ?. Pour toutx??0,π2 ?, on a tan?x= 1 + tan2x >0 donc la fonction tangente est strictement croissante sur l"intervalle?0,π2 ?. Il faut prendre garde au fait que la fonction tangente n"est pas globalement croissante puisqu"il s"agit d"une fonction p´eriodique! x0π2 tan?x= 1 + tan2x1 + tanx+∞ 0 | | | ||||0π4π2π
3π2-π2-π-3π21y= tanx
30Chapitre II- Fonctions circulaires et applications r´eciproquesB Fonctions r
´eciproques des fonctions circulairesB.1 La fonction arcsinus ?D´efinitionLa fonction sinus est continue surRet strictement croissante sur l"intervalle?-π2 ,π2 ?, elle r´ealise doncune bijection de cet intervalle sur son image [-1,1] et on peut d´efinir son application r´eciproque.B.1.1 D´efinition
On appellefonction arcsinus, et on note
Arcsin : [-1,1]→?
-π2 ,π2,x?→Arcsinx ,l"application r´eciproque de la restriction de la fonction sinus `a l"intervalle
-π2 ,π2 .B.1.2 Remarques ?Pour toutx?[-1,1], Arcsinxest la mesure d"anglecompriseentre-π2 etπ2 dont le sinus vautx.?Pour toutx?[-1,1], on a sin?Arcsinx?=x.?Pour toutθ??-π2 ,π2 ?, on a Arcsin?sinθ?=θ.Il faut prendre garde au fait que l"expression Arcsin?sinθ?est d´efinie pour toutθ?Rmais ne vaut
exactementθque lorsqueθ??-π2 ,π2En effet, comme on l"a pr´ecis´e ci-dessus, Arcsin?sinθ?d´esigne la mesure d"angle entre-π2
etπ2 dont le sinus vaut sinθi.e.il s"agit de l"unique r´eelθ0??-π2 ,π2 ?tel qu"il existek?Zavecθ=θ0+2kπ.Par exemple, on a Arcsin?sin?17π8
??=π8´Etude des variations de la fonction arcsinusLes variations de la fonction arcsinus sur l"intervalle [-1,1] sont les mˆemes que celles de la fonction
sinus sur l"intervalle? -π2 ,π2 .x-1 0 1Arcsinx
2 -π2 00 1-1π
22y= Arcsinx
B- Fonctions r´eciproques des fonctions circulaires31B.1.3 Proposition
La fonction arcsinus est d´erivable sur ]-1,1[ et pour toutx?]-1,1[,Arcsin?(x) =1⎷1-x2.D´emonstrationEn effet, pour toutx?]-1,1[, on a
Arcsin
?(x) =1sin ?(Arcsinx)=1cos(Arcsinx).Mais Arcsinx??-π2 ,π2?et la fonction cosinus est positive sur cet intervalle donc cos(Arcsinx)?0.Par cons´equent, on peut ´ecrire
Arcsin
?(x) =1?cos2(Arcsinx)=1?1-sin2(Arcsinx)et la conclusion vient du fait que sin(Arcsinx) =x.B.1.4 Remarque
Le graphe de la fonction arcsinus ayant ´et´e obtenu par sym´etrie, on sait qu"il admet des tangentes
verticales pourx=-1 etx= 1 ainsi qu"une tangente de pente 1 pourx= 0. On retrouve cela avec la d´eriv´ee de Arcsin puisqueArcsin
?(0) = 1,limx→-1+1⎷1-x2= +∞et limx→1-1⎷1-x2= +∞.B.2 La fonction arccosinus
?D´efinitionLa fonction cosinus est continue surRet strictement d´ecroissante sur l"intervalle [0,π], elle r´ealise donc
une bijection de cet intervalle sur son image [-1,1] et on peut d´efinir son application r´eciproque.B.2.1 D´efinition
On appellefonction arccosinus, et on note
Arccos : [-1,1]→[0,π],x?→Arccosx ,l"application r´eciproque de la restriction de la fonction cosinus `a l"intervalle [0,π].B.2.2 Remarques
?Pour toutx?[-1,1], Arccosxest la mesure d"anglecompriseentre 0 etπdont le cosinus vautx.?Pour toutx?[-1,1], on a cos?Arccosx?=x.
32Chapitre II- Fonctions circulaires et applications r´eciproques?Pour toutθ?[0,π], on a Arccos?cosθ?=θ.
Il faut prendre garde au fait que l"expression Arccos?cosθ?est d´efinie pour toutθ?Rmais ne vaut
exactementθque lorsqueθ?[0,π].En effet, comme on l"a pr´ecis´e ci-dessus, Arccos?cosθ?d´esigne la mesure d"angle entre 0 etπdont
le cosinus vaut cosθi.e.il s"agit de l"unique r´eelθ0?[0,π] tel qu"il existek?Zavecθ=θ0+ 2kπ.
Par exemple, on a Arccos?cos?12π5
??=2π5´Etude des variations de la fonction arccosinusLes variations de la fonction arccosinus sur l"intervalle [-1,1] sont les mˆemes que celles de la fonction
cosinus sur l"intervalle [0,π].x-1 0 1Arccosx
2 -π2 00 1-1π
2πy= ArccosxB.2.3 Proposition
La fonction arccosinus est d´erivable sur ]-1,1[ et pour toutx?]-1,1[,Arccos?(x) =-1⎷1-x2.D´emonstrationEn effet, pour toutx?]-1,1[, on a
Arccos
?(x) =1cos?(Arccosx)=1-sin(Arccosx).Mais Arccosx?[0,π] et la fonction sinus est positive sur cet intervalle donc sin(Arccosx)?0. Parcons´equent, on peut ´ecrire
Arccos
?(x) =-1?sin2(Arccosx)=-1?1-cos2(Arccosx)et la conclusion vient du fait que cos(Arccosx) =x.
B- Fonctions r´eciproques des fonctions circulaires33B.2.4 Remarque
Le graphe de la fonction arccosinus ayant ´et´e obtenu par sym´etrie, on sait qu"il admet des tangentes
verticales pourx=-1 etx= 1 ainsi qu"une tangente de pente-1 pourx= 0. On retrouve cela avec la d´eriv´ee de Arccos puisqueArccos
?(0) =-1,limx→-1+-1⎷1-x2=-∞et limx→1--1⎷1-x2=-∞.B.3 La fonction arctangente
?D´efinitionLa fonction tangente est continue et strictement croissante sur ?-π2 ,π2 ?, elle r´ealise donc une bijectionde cet intervalle sur son imageRet on peut d´efinir son application r´eciproque.B.3.1 D´efinition
On appellefonction arctangente, et on note
Arctan :R→?
-π2 ,π2,x?→Arctanx ,l"application r´eciproque de la restriction de la fonction tangente `a l"intervalle
-π2 ,π2 .B.3.2 Remarques ?Pour toutx?R, Arctanxd´esigne donc la mesure d"anglecompriseentre-π2 etπ2 dont la tangente vautx.?Pour toutx?R, on a tan?Arctanx?=x.?Pour toutθ??-π2 ,π2 ?, on a Arctan?tanθ?=θ.Il faut prendre garde au fait que l"expression Arctan?tanθ?est d´efinie pour toutθ?Rmais ne vaut
exactementθque lorsqueθ??-π2 ,π2En effet, comme on l"a pr´ecis´e ci-dessus, Arctan?tanθ?=θd´esigne la mesure d"angle entre-π2
et π2 dont la tangente vaut tanθi.e.il s"agit de l"unique r´eelθ0??-π2 ,π2 ?tel qu"il existek?Zavec θ=θ0+ 2kπ. Par exemple, on a Arctan?tan?15π7 ??=π7´Etude des variations de la fonction arctangenteLes variations de la fonction arctangente surRsont les mˆemes que celles de la fonction tangente sur
l"intervalle?-π2 ,π2 ?.x-∞0 +∞Arctanx
2 -π2 034Chapitre II- Fonctions circulaires et applications r´eciproques-π20π
2y= ArctanxB.3.3 Proposition
La fonction arctangente est d´erivable surRet
pour toutx?R,Arctan?(x) =11 +x2.D´emonstrationPour toutx?R, on a
Arctan
?(x) =1tan ?(Arctanx)=11 + tan2(Arctanx)=11 +x2.B.3.4 Remarque
Le graphe de la fonction arctangente ayant ´et´e obtenu par sym´etrie, on sait qu"il admet une tangente
de pente 1 pourx= 0. On retrouve cela avec la d´eriv´ee de Arctan puisque Arctan ?(0) = 1.B.4 Deux relations remarquables entre les fonctions trigonom´etriquesAu vu de l"analogie entre les graphes des fonctions arcsinus et arccosinus, il est naturel de se demander
s"il n"existe pas un lien entre ces deux fonctions. Ce lien tr`es simple est donn´e par le r´esultat suivant :B.4.1 Proposition
Pour toutx?[-1,1], on a : Arcsin(x) + Arccos(x) =π2 .D´emonstrationOn propose deux d´emonstrations.
?Pour toutx?[-1,1], on posef(x) = Arcsin(x) + Arccos(x). Comme les fonctions arcsinus etarccosinus sont toutes deux d´erivables sur ]-1,1[, la fonctionfest elle-aussi d´erivable sur ]-1,1[
B- Fonctions r´eciproques des fonctions circulaires35 et on a f?(x) = Arcsin?(x) + Arccos?(x) =1⎷1-x2+-1⎷1-x2= 0.Il s"ensuit que la fonctionfest constante sur ]-1,1[. On af(0) = Arcsin(0)+Arccos(0) = 0+π2
=π2doncf(x) =π2pour toutx?]-1,1[.Enfin, les fonctions arcsinus et arccosinus sont toutes deux continues `a droite en-1 doncfestaussi continue `a droite en-1i.e.f(-1) = limx→-1+f(x) =π2
. De mˆeme, les fonctions arcsinus etarccosinus sont toutes deux continues `a gauche en 1 doncfest aussi continue `a gauche en 1i.e.f(1) = limx→1-f(x) =π2
. On a donc bienf(x) =π2 pour toutx?[-1,1].?Soitx?[-1,1], on noteα= Arcsin(x) etβ= Arccos(x), alors sinα= sin?Arcsin(x)?=xcosβ= cos?Arccos(x)?=xOn a donc sinα= cosβd"o`u (c"est une formule de trigonom´etrie classique) sinα= sin?π2
-β?.La fonction arcsinus est `a valeurs dans ?-π2 ,π2 ?doncα??-π2 ,π2 ?. La fonction arccosinus est `avaleurs dans [0,π] doncβ?[0,π], d"o`uπ2 -β??-π2 ,π2 ?.Ainsi, on a sinα= sin?π2 -β?alors queαetπ2 -βsont dans l"intervalle?-π2 ,π2 ?sur lequel lafonction sinus est bijective. Par cons´equentα=π2 -βi.e.α+β=π2 .Voici une autre relation remarquable impliquant cette fois-ci la fonction arctangente.B.4.2 Proposition
Arctan(x) + Arctan?1x
??π2 six >0 π2 six <0D´emonstrationPour toutx >0, on posef(x) = Arctan(x)+Arctan?1x
?. La fonctionfest d´erivable sur chacun desintervalles ]- ∞,0[ et ]0,+∞[ et on a f ?(x) = Arctan?(x) + Arctan??1x -1x 2? =11 +x2+11 + 1xquotesdbs_dbs45.pdfusesText_45[PDF] limite arctan infini
[PDF] equivalent de arctan en l'infini
[PDF] tangente hyperbolique dérivée
[PDF] tableau de conjugaison ce2
[PDF] lettre de motivation sorbonne licence
[PDF] fonction hyperbolique exo7
[PDF] dérivée cosh
[PDF] lettre de motivation stage immobilier débutant
[PDF] les fonctions hyperboliques et leurs réciproques pdf
[PDF] trigo hyperbolique
[PDF] lettre de motivation agence immobilière sans experience
[PDF] up and down tome 4
[PDF] ch(2x)
[PDF] up and down saison 4 pdf
