 La fonction Arctangente
La fonction Arctangente
Pour le calcul la calculatrice utilise l'algorithme CORDIC. Page 3. 5°) Valeurs remarquables. On utilise une lecture inverse du tableau des
 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Formulaire de trigonométrie 1 Fonctions trigonométriques
Formulaire de trigonométrie 1 Fonctions trigonométriques
On peut donner explicitement quelques valeurs remarquables : cos(0) = 1 arctan(x) + arctan(y) = arctan ( x + y. 1 − xy. ) + kπ o`u k = 1 si xy > 1 et x ...
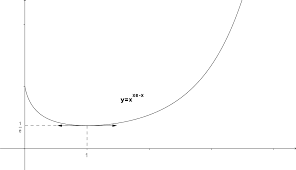 Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Valeurs remarquables de cosinus sinus et tangente. On consid`ere le nombre arctan est dérivable sur R. Il en résulte que f est la composée de deux ...
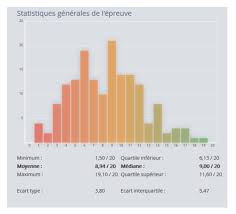 2020 Lépreuve de Calcul et Raisonnement de la session 2020 est
2020 Lépreuve de Calcul et Raisonnement de la session 2020 est
valeurs remarquables de la fonction arctan – et qu'il ne parvenait pas `a les retrouver. Ensuite viennent des calculs classiques de dérivées : `a nouveau ...
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Développements limités usuels en 0
Développements limités usuels en 0
2 Valeurs remarquables π. 6 π. 4 π. 3. 1. 2. √2. 2. √3. 2. 1. 2. 0 π. 2 π. 2. 0 tan x Arctan x + Arctan y = Arctan x + y. 1 − xy+ επ où ε = ⎧⎪⎪⎨. ⎪⎪ ...
 Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
• Valeurs remarquables : ∗ sin(0) = 0. ∗ sin (π. 6 ) = sin (5π. 6 ) = 1. 2 Arctangente f : x ↦→ Arctan(x). • Définition : Réciproque de tan sur ] − π. 2.
 Christine Nazaret
Christine Nazaret
Sinus et cosinus : valeurs remarquables remarquables on tire. Θ=arctan(b/a) [2k π]. Si a<0. On a toujours tan(θ)=b/a mais Θ≠arctan(b/a). Θ=arctan(b/a)+π [2k ...
 Feuille dexercices 7 Fonctions trigonométriques réciproques
Feuille dexercices 7 Fonctions trigonométriques réciproques
< 1 ⇒ 0 = arctan(0) < arctan (. 5. 12. ) < arctan(1) = . 4. Car arctan est remarquables. 6. Tracer le graphe de sur ℝ . Correction exercice 9. 1. Pour ...
 La fonction Arctangente
La fonction Arctangente
Pour le calcul la calculatrice utilise l'algorithme CORDIC. Page 3. 5°) Valeurs remarquables. On utilise une lecture inverse du tableau des
 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
Mathématiques Rappels sur les fonctions usuelles 1. Logarithme f
Valeurs remarquables : ? ln(1) = 0. ? ln(e) = 1 Autres propriétés remarquables : ... ?x ? R+ Arctan(x) ? x (comparaison à la tangente en 0).
 Les-nombres-complexes.pdf
Les-nombres-complexes.pdf
la tangente: Soit z=a+ib non nul. Si a>0. Alors de tan(?)=b/a avec la calculatrice ou le tableau des valeurs remarquables
 Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Devoir de Mathématiques 2 : corrigé Exercice 1. Valeurs
Valeurs remarquables de cosinus sinus et tangente 2. f est la composée de arctan et g donnée par g(t) = sin(t). 1 ? cos(t). : f = arctan ?g.
 Ex_ sur les fonctions trigonométriques réciproques
Ex_ sur les fonctions trigonométriques réciproques
Arctan y x. . Contrôler sur la calculatrice graphique. On pourra comparer et à des valeurs remarquables de Arcsin. • Calculer.
 fonctions-usuelles.pdf
fonctions-usuelles.pdf
f(x)=arcsin(x) g(x)=arccos(x) h(x)=arctan(x)?? a) Fonctions hyperboliques f(x)=sinh(x)g(x)=cosh(x) h(x)=tanh(x)? Sinus et cosinus : valeurs remarquables.
 Les fonctions circulaires réciproques
Les fonctions circulaires réciproques
9 déc. 2020 Remarquons que la fonction Arcsin réciproque d'une bijection impaire
 Feuille dexercices 7 Fonctions trigonométriques réciproques
Feuille dexercices 7 Fonctions trigonométriques réciproques
2 arctan (. 1. 3. ) Correction exercice 2. 1. 0 <. 1. 3. < 1 ? arctan(0) < arctan (. 1. 3. ) < arctan(1). Car arctan est strictement croissante donc.
 Fonctions circulaires et applications r´eciproques
Fonctions circulaires et applications r´eciproques
Quelques valeurs remarquables des fonctions sinus cosinus et tangente Il faut prendre garde au fait que l'expression Arcsin(sin?) est définie pour tout ...
 [PDF] La fonction Arctangente
[PDF] La fonction Arctangente
On utilise une lecture inverse du tableau des valeurs remarquables Nous pouvons également obtenir les valeurs des arctangentes de (cf voir V) x 0 6
 [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
1 mar 2017 · On note arcsin : [?11] ? [??/2 ?/2] la fonction réciproque i e si valeurs intermédiaires pour tout ?1 ? y ? 1 il existe ??/2
 [PDF] Feuille dexercices 7 Fonctions trigonométriques réciproques
[PDF] Feuille dexercices 7 Fonctions trigonométriques réciproques
1 + tan2( ) = 2sin( ) cos( ) × cos2( ) = 2sin( )cos( ) = sin(2 ) 3 sin(2arctan( 1 3 )) = 2tan(arctan ( 1 3))
 [PDF] Formulaire de trigonométrie 1 Fonctions trigonométriques - LPSM
[PDF] Formulaire de trigonométrie 1 Fonctions trigonométriques - LPSM
On peut donner explicitement quelques valeurs remarquables : cos(0) = 1 ; cos (?6) = ?3 2; cos (?4) = ?2 2; cos (?3) = 1 2; cos (?2) = 0 On en déduit
 [PDF] Les fonctions de référence
[PDF] Les fonctions de référence
La fonction Arctan est impaire La démonstration de ce théorème est identique à la démonstration du théorème 14 page 21 Valeurs usuelles de la fonction
 [PDF] Chapitre bonus 1 : Trigonométrie - Julian Tugaut
[PDF] Chapitre bonus 1 : Trigonométrie - Julian Tugaut
Fonctions tangente et arctangente 4 Formules trigonométriques 5 Angles remarquables Elle est `a valeurs dans l'intervalle [?1; 1] Julian Tugaut
 Arc tangente - Vikidia lencyclopédie des 8-13 ans
Arc tangente - Vikidia lencyclopédie des 8-13 ans
Graphe de la fonction arctan La fonction arc tangente est l'application réciproque de la Valeurs remarquables[modifier modifier le wikicode]
 [PDF] Les fonctions circulaires réciproques - MPSI - Camille Guerin
[PDF] Les fonctions circulaires réciproques - MPSI - Camille Guerin
Remarquons que Arctan réciproque d'une fonction impaire est elle aussi impaire Voici quelques valeurs remarquables de la fonction Arctan x 0 ? 3 3
 [PDF] Fonctions trigonométriques réciproques
[PDF] Fonctions trigonométriques réciproques
[ arctan[tan(y)] = y 2) On a aussi : ?x?[-1 ;1] arcsin(-x) = -arcsin(x) et ?x
Comment calculer les valeurs de arctan ?
La règle de la fonction arc tangente de base est f(x)=arctan(x). f ( x ) = arctan ? On note aussi cette fonction f(x)=tan?1(x). f ( x ) = tan ? 1 ?Comment montrer que la fonction arctangente est impaire ?
tan y x = - - . Arctan x y - = - . Arctan Arctan y y - = - . Il en résulte que la fonction Arctan est impaire.Quand on utilise Arcsin ?
Les relations Arcsinus, Arccosinus et Arctangente permettent de calculer la valeur d'un angle aigu d'un triangle rectangle dont on connaît les côtés.- La valeur exacte de arctan(?1) est ??4 . Le résultat peut être affiché en différentes formes.
Les fonctions usuellesLes fonctions usuelles
Objectif :Objectif :
ConnaConna
îître les reprtre les repr
éésentations sentations
graphiques de ces fonctions et graphiques de ces fonctions et leurs proprileurs propriééttéés principaless principales
Les fonctions usuellesLes fonctions usuelles
vues en terminalevues en terminaleLogarithme et exponentielleLogarithme et exponentiellef(x)=ln(x) g(x)=log(x) h(x)=exp(x)=ef(x)=ln(x) g(x)=log(x) h(x)=exp(x)=e
xx Puissances et polynômesPuissances et polynômes f(x)=xf(x)=x g(x)=xg(x)=x h(x)=xh(x)=x ⎷⎷22 k(x)=xk(x)=x --22 l(x)=l(x)= --xx33+2x+2x --33TrigonomTrigonom
éétriquestriques
f(x)=cos(x) g(x)=sin(x) h(x)=tan(x)f(x)=cos(x) g(x)=sin(x) h(x)=tan(x) DD""autres fonctions usuellesautres fonctions usuelles a)a) RRééciproques des fonctions ciproques des fonctions trigonomtrigonoméétriquestriques
f(x)=arcsin(x)f(x)=arcsin(x) g(x)=arccos(x)g(x)=arccos(x) h(x)=arctan(x)h(x)=arctan(x) a)a)Fonctions hyperboliquesFonctions hyperboliques
f(x)=sinh(x)f(x)=sinh(x) g(x)=cosh(x)g(x)=cosh(x) h(x)=tanh(x)h(x)=tanh(x) Logarithmes et exponentielleLogarithmes et exponentielle▪▪Logarithme nLogarithme nééppéérienrien
▪▪Autres logarithmesAutres logarithmes▪▪exponentielleexponentielleLogarithme nLogarithme n
ééppéérienrien
DDééfinition : la fonction logarithme nfinition : la fonction logarithme nééppéérien notrien not
éée e lnln
ddééfinie sur finie sur ]0;+]0;+ est la fonction telle que est la fonction telle que sa dsa déérivriv
ééeeest est
1/x1/x
ln(1)=0ln(1)=0Propriétés :ln(ab)=ln(a)+ln(b) ln(a/b)=ln(a)-ln(b) ln(aα)=αln(a)
Autres LogarithmesAutres Logarithmes
▪▪Logarithme dLogarithme déécimalcimal
log(x)=ln(x)/ln(10)log(x)=ln(x)/ln(10) log(10)=1log(10)=1▪▪Logarithme de base a>0 et aLogarithme de base a>0 et a ≠≠11 loglog aa(x)=ln(x)/ln(a)(x)=ln(x)/ln(a) loglog aa(a)=1(a)=1ExponentielleExponentielle
DDééfinition : La fonction rfinition : La fonction r ééciproque de ln est la ciproque de ln est la fonction exponentiellefonction exponentielle ;0)ln( yyx xey xPropriétés :exp"(x)=exp(x)
e0=1 e1=2,718... ea+b =e aeb e-a=1/e a era=(e a)r Puissances et polynômesPuissances et polynômes ▪▪Fonctions puissances :Fonctions puissances :CarrCarréé, cube,, cube,
GGéénnééralisationralisation
▪▪Fonctions polynômesFonctions polynômesLes fonctions puissancesLes fonctions puissances
Cas particuliers :
•Si n est un entier positif x n •Si k est un entier relatif x k •Si r est un rationnel x rCas général
Si a est un réel,
xxaaCarrCarr
▪▪DDééfinition : la fonction carrfinition : la fonction carrééest dest d
ééfinie pour tout x finie pour tout x
rrééel par el par xx22=x.x=x.xPropriétés :
PaireNon bijective sur R
Réciproque sur [0,+
notéeDérivée: 2x
CubeCube
▪▪DDééfinition : la fonction cube est dfinition : la fonction cube est dééfinie pour tout finie pour tout
x rx rééel parel par
xx33=x.x.x=x.x.xPropriétés :
Impaire
Bijective
La réciproque est racine
cubiqueDérivée: 3x
2Fonction xFonction x
nnavec n entier positifavec n entier positif ▪▪DDééfinition : pour tout x rfinition : pour tout x rééel el
xxnn=x=x .x (n fois).x (n fois)Propriétés :
Si n est pair (impair), la fonction est
paire (impaire)Réciproque sur [0,+
∞[: fonction racine nième 0 0yyx xxy nnDérivée: nx
n-1Fonction Fonction
xx--nnavec n avec n entierentier positifpositifSi n Si n
entierentier positifpositif , , xx--nn=1/x=1/x nnExempleExemple
: x: x --22=1/x=1/x22=1/(x.x)=1/(x.x)
pour xpour x ≥≥0, x0, x1/n1/n==nn⎷⎷xx(racine ni(racine ni
èème)me)
Exemple : xExemple : x
1/21/2==⎷⎷xx
Si r=p/q, alors xSi r=p/q, alors x
rr==qq⎷⎷xxppExemples : pour x>0, xExemples : pour x>0, x
--1/21/2=1/=1/ ⎷⎷xx pour xpour x ≥≥0, x0, x5/25/2==⎷⎷xx55
pour tout x, xpour tout x, x2/32/3==33⎷⎷xx2 2
DDéérivriv
ééeede de
xxrr: rx: rx rr--11GGéénnééralisation : xralisation : x
a a avec a ravec a rééelel
▪▪DDééfinition : Soit a un rfinition : Soit a un rééel el
pour x>0 pour x>0 xxaa=e=e a ln(x)a ln(x) Propriétés: Soient a et b deux réels, x>0 et y>0 1 a=1 xa+b =x axb xa)b=x ab x-a=1/x a (xy) a=x ayaDérivée: ax
a-1PolynômesPolynômes
Exemple : p(x)=xExemple : p(x)=x
2424++⎷⎷3x3x
44--x/3 est un polynôme de degrx/3 est un polynôme de degr
éé24.24.
Les polynômes sont souvent utilisLes polynômes sont souvent utiliséées parce que ce sont es parce que ce sont
les fonctions les plus simplesles fonctions les plus simplespp""(x)=24x(x)=24x2323+4 +4
⎷⎷3x3x33--1/31/3
limite en +limite en + de p(x)= limite en +de p(x)= limite en + de xde x 2424les polynômes de degrles polynômes de degr
ééinfinf
éérieur ou rieur ou
éégal gal
àànnsont des sont des
fonctions dont la fonctions dont la ddéérivrivééee((nn+1)i+1)i
èème est nulle.me est nulle.
pp(25)(25) (x)=0(x)=0 Un aspect important en calcul numUn aspect important en calcul numéérique est la rique est la
possibilitpossibilit ééd"d"éétudier les fonctions compliqutudier les fonctions compliquéées au moyen es au moyen
d"approximations par des polynômes. d"approximations par des polynômes. Quelques limites classiquesQuelques limites classiquesQuand xQuand x
ln(x)/x ln(x)/x 00 eexx/x/x ""La fonction exp lLa fonction exp l ""emporte sur puissance emporte sur puissance qui lqui l ""emporteemporte sur sur logarithmelogarithme en enQuand xQuand x
00 x ln(x)x ln(x) 0 0 ln(x+1)/xln(x+1)/x 11Fonctions trigonomFonctions trigonom
éétriquestriques
Cosinus, sinus et tangente dans le Cosinus, sinus et tangente dans le triangle rectangletriangle rectangle ▪▪cos(cos( ÂÂ) = longueur de côt) = longueur de côtééadjacent / longueur adjacent / longueur
de l"hypotde l"hypotéénuse = nuse =
aa//hh.. ▪▪sin(sin( ÂÂ) = longueur du côt) = longueur du côtééopposoppos
éé/ longueur / longueur
de l"hypotde l"hypotéénuse = nuse =
oo//hh. . ▪▪tan(tan( ÂÂ) = longueur du côt) = longueur du côtééopposoppos
éé/ longueur / longueur
du côtdu côtééadjacent = adjacent =
oo//aa. . oh a Sinus et cosinus : valeurs Sinus et cosinus : valeurs remarquablesremarquables Non defini⎷311/⎷30tan01/2⎷2/2⎷3/21cos1
Sinus et cosinus : formules Sinus et cosinus : formules fondamentalesfondamentalesFormules de trigonomFormules de trigonom
éétrietrie
sinsin²²(x)+cos(x)+cos
²²(x)=1(x)=1
sin(asin(a±±b)=sin(a)cos(b) b)=sin(a)cos(b)
±±sin(b)cos(a)sin(b)cos(a)
coscos --/+sin(a)sin(b)/+sin(a)sin(b)Formules dFormules d
""Euler et de MoivreEuler et de Moivre cos(a)=(ecos(a)=(e iaia+e+e --iaia)/2)/2 sin(a)=(esin(a)=(e iaia--ee--iaia)/(2i))/(2i) (e(e ixix))bb=cos(bx)+i sin(bx)=cos(bx)+i sin(bx)SinusSinus
PropriPropri
ééttéés : Rs : R
--1;1] 1;1]PPéériode 2riode 2
impaireimpairesin(0)=0sin(0)=0sinsin ""(x)=cos(x)(x)=cos(x)Limite x Limite x
00 sin(x)/x sin(x)/x 11Pas de limite en Pas de limite en
CosinusCosinus
PropriPropri
ééttéés : Rs : R
-->[>[--1;1]1;1]PPéériode 2riode 2
PairePairecos(0)=1cos(0)=1coscos
""(x)=(x)= --sin(x)sin(x)Limite x Limite x
00 (cos(x)(cos(x) --1)/x 1)/x 00Pas de limite en lPas de limite en l
""infiniinfiniTangenteTangente
PropriPropri
ééttéés :s :
PPéériode riode
impaireimpairetantan ""(x)=1+tan(x)=1+tan²²(x)=1/(x)=1/
coscos²²(x)(x)
Définition : pour tout x réel tel que cos(x)≠0tan(x)=sin(x)/cos(x) Reciproques des fonctions Reciproques des fonctions trigonomtrigonoméétriquestriques
ArcsinusArcsinus
DDééfinition : arcsinus est la rfinition : arcsinus est la r ééciproque de la restriction de ciproque de la restriction de sinus : [sinus : [ --ππ/2;/2;ππ/2]/2]
[[--1;1]. Elle se note arcsin1;1]. Elle se note arcsinPP-Î=Û???
]2/;2/[)sin( ]1;1[)arcsin( yyx xxyPour -1 Arcsin"(x)=1/
⎷(1-x²) ArccosinusArccosinus
▪▪DDééfinition : arccosinus est la rfinition : arccosinus est la r ééciproque de la ciproque de la
restriction de cosinus : [0;restriction de cosinus : [0; [[--1;1]. Elle se note 1;1]. Elle se note arccosarccos PÎ=Û???
];0[)cos( ]1;1[)arccos( yyx xxy Pour -1 Arccos"(x)= - 1/
⎷(1-x²) ArctangenteArctangente
▪▪Arctangente est la Arctangente est la fonction rfonction r ééciproqueciproque
de la de la restrictionrestriction de la de la fonction tangentefonction tangente ààl"intervalle l"intervalle
½½ππ; ; ½½ππ[[. Elle se note . Elle se note arctanarctan PP-Î=Û???
[2/;2/])tan()arctan( yyx Rxxy Pour tout x réel,
Arctan"(x)=1/(1+x²)
Fonctions hyperboliquesFonctions hyperboliques
▪▪Sinus hyperboliqueSinus hyperbolique▪▪Cosinus hyperboliqueCosinus hyperbolique▪▪Tangente hyperboliqueTangente hyperbolique
Sinus hyperboliqueSinus hyperbolique
Définition : pour tout x réel
sinh(x)=(e x-e-x)/2 impaire, strict croissante fonction bijective de R->R : réciproque x->argsh(x) Cosinus hyperboliqueCosinus hyperbolique
Définition : pour tout x réel
cosh(x)=(e x+e -x)/2 Propriétés principales :
ch²(x)- sh²(x)=1 sh"(x)=ch(x) ch"(x)=sh(x) fonction paire, non bijective TangenteTangente
hyperboliquehyperbolique Définition : pour tout x réel
tanh(x)=sinh(x)/cosh(x) tanh"(x)=1/ch 2(x)=1-th
2(x)quotesdbs_dbs45.pdfusesText_45
Arcsin"(x)=1/
⎷(1-x²)ArccosinusArccosinus
▪▪DDééfinition : arccosinus est la rfinition : arccosinus est la rééciproque de la ciproque de la
restriction de cosinus : [0;restriction de cosinus : [0; [[--1;1]. Elle se note 1;1]. Elle se note arccosarccosPÎ=Û???
];0[)cos( ]1;1[)arccos( yyx xxyPour -1 Arccos"(x)= - 1/
⎷(1-x²) ArctangenteArctangente
▪▪Arctangente est la Arctangente est la fonction rfonction r ééciproqueciproque
de la de la restrictionrestriction de la de la fonction tangentefonction tangente ààl"intervalle l"intervalle
½½ππ; ; ½½ππ[[. Elle se note . Elle se note arctanarctan PP-Î=Û???
[2/;2/])tan()arctan( yyx Rxxy Pour tout x réel,
Arctan"(x)=1/(1+x²)
Fonctions hyperboliquesFonctions hyperboliques
▪▪Sinus hyperboliqueSinus hyperbolique▪▪Cosinus hyperboliqueCosinus hyperbolique▪▪Tangente hyperboliqueTangente hyperbolique
Sinus hyperboliqueSinus hyperbolique
Définition : pour tout x réel
sinh(x)=(e x-e-x)/2 impaire, strict croissante fonction bijective de R->R : réciproque x->argsh(x) Cosinus hyperboliqueCosinus hyperbolique
Définition : pour tout x réel
cosh(x)=(e x+e -x)/2 Propriétés principales :
ch²(x)- sh²(x)=1 sh"(x)=ch(x) ch"(x)=sh(x) fonction paire, non bijective TangenteTangente
hyperboliquehyperbolique Définition : pour tout x réel
tanh(x)=sinh(x)/cosh(x) tanh"(x)=1/ch 2(x)=1-th
2(x)quotesdbs_dbs45.pdfusesText_45
Arccos"(x)= - 1/
⎷(1-x²)ArctangenteArctangente
▪▪Arctangente est la Arctangente est la fonction rfonction rééciproqueciproque
de la de la restrictionrestriction de la de la fonction tangentefonction tangenteààl"intervalle l"intervalle
½½ππ; ; ½½ππ[[. Elle se note . Elle se note arctanarctanPP-Î=Û???
[2/;2/])tan()arctan( yyx RxxyPour tout x réel,
Arctan"(x)=1/(1+x²)
Fonctions hyperboliquesFonctions hyperboliques
▪▪Sinus hyperboliqueSinus hyperbolique▪▪Cosinus hyperboliqueCosinus hyperbolique▪▪Tangente hyperboliqueTangente hyperbolique
Sinus hyperboliqueSinus hyperbolique
Définition : pour tout x réel
sinh(x)=(e x-e-x)/2 impaire, strict croissante fonction bijective de R->R : réciproque x->argsh(x)Cosinus hyperboliqueCosinus hyperbolique
Définition : pour tout x réel
cosh(x)=(e x+e -x)/2Propriétés principales :
ch²(x)- sh²(x)=1 sh"(x)=ch(x) ch"(x)=sh(x) fonction paire, non bijectiveTangenteTangente
hyperboliquehyperboliqueDéfinition : pour tout x réel
tanh(x)=sinh(x)/cosh(x) tanh"(x)=1/ch2(x)=1-th
2(x)quotesdbs_dbs45.pdfusesText_45[PDF] limite arctan infini
[PDF] equivalent de arctan en l'infini
[PDF] tangente hyperbolique dérivée
[PDF] tableau de conjugaison ce2
[PDF] lettre de motivation sorbonne licence
[PDF] fonction hyperbolique exo7
[PDF] dérivée cosh
[PDF] lettre de motivation stage immobilier débutant
[PDF] les fonctions hyperboliques et leurs réciproques pdf
[PDF] trigo hyperbolique
[PDF] lettre de motivation agence immobilière sans experience
[PDF] up and down tome 4
[PDF] ch(2x)
[PDF] up and down saison 4 pdf
