 Mécanique 4 Solide en rotation autour dun axe fixe. Table des
Mécanique 4 Solide en rotation autour dun axe fixe. Table des
Nous avons pour l'instant étudié qu'un seul type d'étude dynamique : celle d'un point matériel. Cette étude peut se généraliser simplement au cas des
 CHAPITRE 11. DYNAMIQUE DU SOLIDE
CHAPITRE 11. DYNAMIQUE DU SOLIDE
28/03/2023 11.32.) où est l'accélération angulaire du solide. о ε. C'est la loi de la dynamique pour les solides en rotation autour d'un axe fixe. La ...
 Polycopié dexercices et examens résolus: Mécaniques des
Polycopié dexercices et examens résolus: Mécaniques des
Appliquer le principe fondamental de la dynamique au solide 3 dans son mouvement par (solide en rotation autour d'un axe fixe. /RG). Théorème du moment ...
 Chapitre XI - SOLIDE EN ROTATION AUTOUR DUN AXE FIXE.
Chapitre XI - SOLIDE EN ROTATION AUTOUR DUN AXE FIXE.
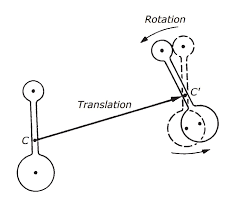
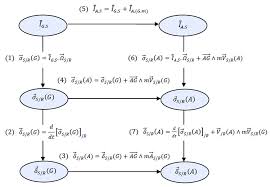
Pour une généralisation ultérieure et `a cause d'une ressemblance avec les formules de changement de point pour les moments cinétique et dynamique on va
 FICHE - Dynamique et énergétique.pdf
FICHE - Dynamique et énergétique.pdf
Un solide est dit équilibré lors de sa rotation autour d'un axe fixe si et seulement si : Equilibrage statique : - Son centre de masse est sur l'axe de rotation
 Introduction 1. Solide en rotation autour dun axe fixe
Introduction 1. Solide en rotation autour dun axe fixe
solide autour d'un axe fixe. Equilibrage statique et dynamique. Exemples. (1er CU). Introduction. 1. Solide en rotation autour d'un axe fixe. 1.1. Réalisation ...
 mecanique2 cinetique et dynamique du solide 2a mp 2016
mecanique2 cinetique et dynamique du solide 2a mp 2016
SOLIDE EN ROTATION AUTOUR D'UN AXE FIXE : I). MOMENT CINÉTIQUE D'UN SOLIDE EN ROTATION AUTOUR D'UN AXE FIXE : 1) Moment d'inertie d'un solide par rapport à un ...
 Pendules mecaniques.pdf
Pendules mecaniques.pdf
En physique un pendule est un corps solide pouvant osciller autour d'un point ou d'un axe fixe et Figure 4: Solide en rotation autour d'un axe passant par le ...
 4. DYNAMIQUE DU SOLIDE INDEFORMABLE
4. DYNAMIQUE DU SOLIDE INDEFORMABLE
L'application du Principe Fondamentale de la Dynamique à un solide (S) effectuant un mouvement de rotation autour d'un axe fixe permet de démontrer que
 FICHE Liens SI & Sciences Ph FicheLien-LoiDeNEWTON-PFD.docx
FICHE Liens SI & Sciences Ph FicheLien-LoiDeNEWTON-PFD.docx
○ Solide en rotation autour d'un axe fixe dont sur l'axe de rotation ental de la dynamique pour les mouvements de rotation autour d'un axe fixe.
 Mécanique 4 Solide en rotation autour dun axe fixe. Table des
Mécanique 4 Solide en rotation autour dun axe fixe. Table des
Nous avons pour l'instant étudié qu'un seul type d'étude dynamique : celle d'un point matériel. Cette étude peut se généraliser simplement au cas des
 Polycopié dexercices et examens résolus: Mécaniques des
Polycopié dexercices et examens résolus: Mécaniques des
Géomètrie des masses. Cinétique du solide
 CHAPITRE 11. DYNAMIQUE DU SOLIDE
CHAPITRE 11. DYNAMIQUE DU SOLIDE
17 août 2022 Equation du mouvement dans le cas de la rotation d'un solide (autour d'un axe fixe). . . - 11.5 -. 11.4. Principe de d'Alembert .
 CH3 : Solide en mouvement de rotation autour dun axe fixe
CH3 : Solide en mouvement de rotation autour dun axe fixe
Quelle solution technique peut-on apporter ? Rapport au programme : A3. SOLIDE ET FLUIDE EN MOUVEMENT. A3.1. Principe fondamental de la dynamique appliqué au
 Chapitre XI - SOLIDE EN ROTATION AUTOUR DUN AXE FIXE.
Chapitre XI - SOLIDE EN ROTATION AUTOUR DUN AXE FIXE.
Pour une généralisation ultérieure et `a cause d'une ressemblance avec les formules de changement de point pour les moments cinétique et dynamique on va
 06.02 - Dynamique dun solide en rotation - Equilibrage
06.02 - Dynamique dun solide en rotation - Equilibrage
1 Etude dynamique d'un solide en rotation autour d'un axe fixe. Paramétrage du problème : On considère un solide S1 quelconque de centre d'inertie G
 mouvements de rotation dun solide
mouvements de rotation dun solide
Étude en dynamique. Mouvement circulaire uniforme. Solide en rotation autour d'un axe fixe ? et soumis à une force de moment constant.
 CH08 : Solide en mouvement de rotation autour dun axe fixe
CH08 : Solide en mouvement de rotation autour dun axe fixe
CH08 : Solide en mouvement de rotation autour d'un axe fixe. Enjeu : Mise en sécurité d'une machine-outil. Problématique : En tant que responsable de la
 mecanique2 cinetique et dynamique du solide 2a mp 2016
mecanique2 cinetique et dynamique du solide 2a mp 2016
où r est la distance du point M de (S) à l'axe théorème : si un solide (S) est en rotation autour d'un axe fixe ? d'un référentiel R alors :.
 Introduction 1. Solide en rotation autour dun axe fixe
Introduction 1. Solide en rotation autour dun axe fixe
Leçon n°4 : Mouvement d'un solide autour d'un axe fixe. Equilibrage statique et dynamique. Exemples. (1er CU). Introduction. 1. Solide en rotation autour
 [PDF] SOLIDE EN ROTATION AUTOUR DUN AXE FIXE - Joël SORNETTE
[PDF] SOLIDE EN ROTATION AUTOUR DUN AXE FIXE - Joël SORNETTE
simple : celui o`u le solide tourne autour d'un axe fixe Il en est de même pour la somme en un point M des moments dynamiques : ??? Mint(M) =
 [PDF] solide-en-rotation-autour-d-un-axe-fixe-courspdf - AlloSchool
[PDF] solide-en-rotation-autour-d-un-axe-fixe-courspdf - AlloSchool
Dans les mouvements de rotation il est préférable d'utiliser le théorème du moment cinétique Pour un solide en rotation autour d'un axe fixe : ? ? ?
 [PDF] Mécanique 4 Solide en rotation autour dun axe fixe - Pierre Adroguer
[PDF] Mécanique 4 Solide en rotation autour dun axe fixe - Pierre Adroguer
Nous allons dans ce chapitre essayer de décrire la mécanique du solide dans certains cas simples en particulier la rotation d'un solide autour d'un axe fixe (
 [PDF] CH08 : Solide en mouvement de rotation autour dun axe fixe
[PDF] CH08 : Solide en mouvement de rotation autour dun axe fixe
Qu'est-ce qu'un solide en rotation ? Un solide est en rotation autour d'un axe fixe si tous les points du solide ont même vitesse angulaire Un rotor mobile
 [PDF] mouvements de rotation dun solide
[PDF] mouvements de rotation dun solide
Étude en dynamique Mouvement circulaire uniforme Solide en rotation autour d'un axe fixe ? et soumis à une force de moment constant
 [PDF] Introduction 1 Solide en rotation autour dun axe fixe
[PDF] Introduction 1 Solide en rotation autour dun axe fixe
Leçon n°4 : Mouvement d'un solide autour d'un axe fixe Equilibrage statique et dynamique Exemples (1er CU) Introduction 1 Solide en rotation autour
 [PDF] CHAPITRE 11 DYNAMIQUE DU SOLIDE
[PDF] CHAPITRE 11 DYNAMIQUE DU SOLIDE
28 mar 2023 · Dans ce chapitre nous allons étudier le mouvement de rotation d'un solide autour d'un axe qui passe soit par un point fixe dans un référentiel
 [PDF] solution_exercices de Mouvement de rotation dun solide autour d
[PDF] solution_exercices de Mouvement de rotation dun solide autour d
Mouvement de rotation autour d'un axe fixe ZEGGAOUI EL MOSTAFA Exercice_1 l'équation horaire d'un point La relation fondamentale de la dynamique
 [PDF] Mouvement de rotation - Chimie Physique
[PDF] Mouvement de rotation - Chimie Physique
La vitesse angulaire du point M d'un solide en mouvement de rotation autour d'un axe fixe est ?? = 10rad/s; (a) Calculer l'accélération angulaire du point M;
 [PDF] Mouvement de rotation dun solide autour dun axe fixe
[PDF] Mouvement de rotation dun solide autour dun axe fixe
Lorsqu'un corps est en rotation autour d'un axe fixe tous ses points (sauf les points constituant l'axe de rotation) sont animés de mouvements circulaires
Quand Dit-on qu'un solide est en rotation autour d'un axe fixe ?
Un solide indéformable poss? un mouvement de rotation autour d'un axe fixe si le mouvement de chacun de ses points est circulaire centré sur cet axe et la trajectoire de ces points mobiles appartient au plan orthogonal avec l'axe de rotation.Comment provoquer la rotation d'un solide autour d'un axe ?
Le moment d'une force par rapport à son axe de rotation s'exprime par M?( ) = F × d, donc plus la longueur d du bras de levier est grande et plus le moment de la force sera élevé. La force aura ainsi une plus grande efficacité pour faire tourner le solide autour de son axe de rotation.Quand utiliser le PFD ?
Le PFD est appliqué uniquement lorsqu'un solide est en rotation autour d'un axe fixe. L'axe de rotation passe par le centre de gravité du solide qui se trouve sur cet axe.- Un solide est en rotation si la trajectoire de tous ses points sont des cercles dont les centres sont sur une même droite ; cette droite est appelée « axe de rotation », et habituellement notée ?.
Leçon 4 25
Leçon n°4 : Mouvement d'un solide autour d'un axe fixe. Equilibrage statique et dynamique. Exemples. (1 er CU)Introduction
1. Solide en rotation autour d'un axe fixe
1.1. Réalisation pratique
1.2. Equations du mouvement
1.3. Liaison parfaite
1.4. Exemple : Le pendule pesant
1.5. Autres exemples
2. Equilibre statique et dynamique
2.1. Equilibrage statique
2.2. Equilibrage dynamique
2.3. Exemple : Equilibrage statique et dynamique d'une roue de voiture
Conclusion
Introduction
Dans cette leçon nous appliquons le théorème de la résultante cinétique (TRC) et le théorème du
moment cinétique (TMC) à un solide S en rotation autour d'un axe fixe, dans un référentiel galiléen.
Les relations obtenues, écrites dans un référentiel fixe par rapport au solide S, mettent en évidence
des actions de contact du solide sur son support, dépendantes du mouvement du solide et pouvantêtre très importantes.
Afin d'éviter une usure prématurée des contacts de la liaison, nous verrons comment équilibrer le
solide en rotation1. Solide en rotation autour d'un axe fixe
1.1. Réalisation pratique
Considérons un solide S de masse m, en rotation autour d'un axe fixe Oz dans un référentiel galiléen
R = Oxyz. Ce solide n'a qu'un seul degré de liberté angulaire. La liaison permettant cette rotation est
une liaison pivot. Elle peut être réalisée en utilisant différents types de contact : !"Deux contacts ponctuels sur l'axe Oz, principalement en horlogerie. !"Deux roulements à billes. !"Deux rotules. !"Contact par coussin d'air ou coin d'huile. !"Contact à couteau, pour les balances.1.2. Equations du mouvement
Le référentiel tournant R' = Ox'y'z est fixe par rapport au solide S et l'angle θ entre les axes Ox et Ox' repère la position de S. On note CCO [, ]RM et O [, ]RM les torseurs au point O des forces de contact et des autres forces agissant sur S, et la distance à l'axeOz du centre de masse C ; HC = a.
!"Appliquons le TRC à S, dans le référentiel galiléen R : CCR m=+aRR. C H Oθ x
x' y y' z S a26 leçon 4
Or2222CR R R
(d dt ) (d dt )==aOC HC et en projection sur les axes Ox', Oy', et Oz du repère R', leTRC s'écrit :
2Cx' x'
Cy' y'
Czz ma R R ma R R0R R-θ=+
!"Appliquons le TMC à S, dans le référentiel galiléen R : COOO R d dt()=+()()σσσσMM.
Or OO [I]=σωσωσωσω où O [I] est la matrice d'inertie en O et ω=θ! la vitesse de rotation de S suivant l'axe Oz.Dans le référentiel tournant R',
O [I] s'écrit :Ox' x'y' x'z
Oy'x'Oy'y'z
zx' zy' Oz III [I] I I I III?? Les moments d'inertie de S par rapport aux axes Ox', Oy' et Oz sont constants et ont pour expressions : 22Ox'I(y'z)d=+
22Oy'I(zx')d=+
et 22OzI(x'y')d=+
ainsi que les produits d'inertie : x'y'Ix'y'd=
y'zIy'zd=
et zx'Izx'd=
On en déduit les composantes du moment cinétique Oσσσσ exprimées dans R' :
x'z Oy'z Oz I II-θ
La matrice d'inertie étant constante dans R', le calcul de la dérivée du moment cinétique
Oσσσσ dans R'
ne fait intervenir que les dérivées de la vitesse angulaire. En utilisant la relation de dérivation d'un
vecteur dans un référentiel mobile : OOO RR' dd dt dt()()=+?()()()()σσ on obtient les composantes de la dérivée du moment cinétique OR (d dt)σσσσdans R'. Finalement, en projection sur les axes Ox', Oy' et Oz de R', le TMC s'écrit :2Cx'z y'z Ox' Ox'
2Cy'z x'z Oy' Oy'
COz Oz Oz
II III-θ+θ= +
!!MM MM MMLeçon 4 27
Nous avons obtenu six équations par application du TRC et du TMC. Mais les inconnues sont au nombre de sept ; Six pour le torseur des forces de contact CCO [, ]RM et une pour l'angle de rotation θ.Il faut donc une équation supplémentaire pour résoudre le problème. C'est l'hypothèse d'une liaison
parfaite qui va nous la fournir.1.3. Liaison parfaite
Le travail des forces de contact, non conservatives, est :CCNC O O
Wdtdtδ=? +?vRωωωωM.
Si la liaison entre le solide et son support est parfaite, NCW0δ=. Au point O de l'axe de rotation 0z,
O =v0 et donc CO0?=ωωωωM. On en déduit une septième équation :
COz 0=M. Suivant l'axe Oz, le TMC fournit alors l'équation du mouvement : Oz OzIθ=!!M.
Cette équation s'obtient également à partir du théorème de l'énergie cinétique, pour un système
conservatif , C dE W=δ avec :2CCOz Oz
dE1EI I2dt=θ? =θθ!!!! et Oz W dtδ=θ!M.D'où :
Oz OzIθ=!!M.
1.4. Exemple : Le pendule pesant
1.4.1. Le pendule non amorti
Le solide S de masse m, est en rotation autour de l'axe horizontal fixe Oz. Il est soumis à la pesanteur et aux forces de contact dues à réactions du support sur l'axe de rotation. Si l'on considère la liaison parfaite le moment des forces de contact est nulle ; COz0=M, et d'après la figure :
Oz mgasin=- θM. L'équation du mouvement s'écrit : OzImgasin0θ+ θ=!!.
L'énergie cinétique est
2COzE(12)I=θ! et l'énergie
potentielle PEmga(1cos)=-θ en prenant
PE0= pour
0θ=. D'autre part, la conservation de l'énergie permet
d'écrire :CMECAP
EE E=-.
Les différents mouvements du pendule s'observent sur la figure ci-contre. !"Si MECAE2mga>, le pendule effectue un nombre de
tour illimité, le mouvement est révolutif. !"Si MECA0 E 2mga<<, le pendule oscille autour de
l'angle 0θ=.Dans le cas particulier où
MECA0 E 2mga<", les
oscillations ont de faibles amplitudes et sinθ≈θ.L'oscillateur est harmonique de période :
y' y x x' z C m g θO a P E MECA E 0 0 0 -θπ -π 2mga28 leçon 4
Oz 0IT2mga=π.
On dit qu'il y a isochronisme des petites oscillations car la période ne dépend pas de l'amplitude des
oscillations.Envisageons maintenant le cas où l'amplitude des oscillations est importante. On lâche le pendule
sans vitesse initiale d'une position repéré par l'angle 0 θ. La période des oscillations se calcule à partir de l'intégrale première de l'énergie : 2 Oz 01dImga(coscos)2dtθ
En intégrant sur un quart de période, entre 0 et 0 θ, on obtient l'expression de la période T : 0 0 0 02TdTcos cos
et en utilisant les développements limités : 200TT116
Il n'y a plus isochronisme des oscillations.
!"Si MECAE0<, le mouvement est impossible.
On peut également représenter le portrait des phases de ce pendule non amorti :1.4.2. Le pendule amorti
Si le pendule est amorti par des forces de frottement visqueux, dues à la résistance de l'air par
exemple, le momentquotesdbs_dbs45.pdfusesText_45[PDF] les différents types de codification
[PDF] ceb solides et figures 2013
[PDF] ceb solides et figures 2017
[PDF] faut il obeir a une loi injuste
[PDF] ceb solide et figure 2014
[PDF] le poivre est il soluble dans l'eau
[PDF] l'eau est un solvant 5ème evaluation
[PDF] l'eau est un solvant polaire
[PDF] l'eau est un solvant organique
[PDF] eau solvant polaire ou apolaire
[PDF] pourquoi on ne tombe pas alors que la terre est ronde
[PDF] attraction terrestre
[PDF] éducation civique cycle 3 fiches à photocopier
[PDF] guernica pablo picasso español
