[PDF] Ch31-AC Circuits.pdf

View - Download Ch31-AC Circuits.pdf

Previous PDF

Next PDF

Chapter 31

Alternating Current

Circuits

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 2 Alternating Current Circuits•Alternating Current - Generator

Wave Nomenclature & RMS

AC Circuits: Resistor; Inductor; Capacitor

Transformers - not the movie

LC and RLC Circuits - No generator

Driven RLC Circuits - Series

Impedance and Power

RC and RL Circuits - Low & High Frequency

RLC Circuit - Solution via Complex Numbers

RLC Circuit - Example

Resonance

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 3

Generators

By turning the coils in the magnetic field an emf is generated in the coils thus turning mechanical energy into alternating (AC) power. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 4

Generators

Rotating the Coil in a Magnetic Field Generates an Emf •Examples: Gasoline generator

Manually turning the crank

Hydroelectric power

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 5

Generators

m m m peak peak

φ= NBAcosθ θ=ωt

φ= NBAcosωt

d= - φ = NBAωsinωtdt = sinωt; = NBAωε MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 6Wave Nomenclature and RMS

Values

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 7

Wave Nomenclature

A peak-peak = Ap-p = 2Apeak = 2Ap; Ap = Ap-p /2 MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 8 ? ?? ?? ?? ?? ?sinx = A ωt -cos{ } sin tx = A 2π-cos T( )( )

π2π π2 2

x = A sin ωt - x = A sinωt cos - sin cosωt x = A sinωt (0)-(1)cosωt x = -Acosωt

The minus sign means that the

phase is shifted to the right.

A plus sign indicated the phase

is shifted to the left

Shifting Trig Functions

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 9

Shifting Trig Functions

t - = 02 t =2π1 1 Tt = ; =2ω ω 2π

T Tt = =2 2π

4

πsin ωt - = 02

Shifted Trig Functions

-1.50-1.00-0.500.000.501.001.50 -3.00 -2.00 -1.00 0.00 1.00 2.00 3.00 Time sin(

ωt)

sin(

ωt-δ)

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 10

Root Mean Squared

Procedure

•Square it (make the negative values positive)

Take the average (mean)

Take the square root (undo the squaring operation)The root mean squared (rms) method of averaging is used when a variable will average to zero but its effect will not average to zero.

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 11

Sine Functions

-1.5-1.0-0.50.00.51.01.5

0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0

Angle (Radians)

SIN(Theta)SIN2(Theta)RMS Value

Root Mean Squared Average

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 12

Average of a Periodic Function

∫ ∫ ∫T avg p o cos(

ωT)T

ωT p p avg p o 0 cos(0) p avg

1V =V = V(t)dt; V(t)=V sinωtT

V V

1V = V sin

ωtdt = sinxdx = - d(cosx)

T ωTωT

VV = - (1-1)= 0ωT

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 13

Root Mean Squared( )

∫T 2 2 2 pavgo 2 2 2 T p p p 2 2 avgo 2 p 2 avg 2

RMS p pavg1V = V = V (t)dt; V(t)=V sinωtT

V V VV = sin ωtdt = π = T ωT 2 VV =2 1

V V = V = 0.707V2

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 14

Root Mean Squared

2

RMS p pavg

1 V V = V = 0.707V2

Root Square

Mean The RMS voltage (VRMS )is the DC voltage that has the same effect as the actual AC voltage. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 15

RMS Power

The average AC power is the product of the DC equivalent voltage and current. avg p p p p

RMS RMS

avg RMS RMS avg RMS RMS

1P = V I2

V Isince V = and I =2 2

1P = 2 V 2 I2

P =V I

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 16Resistor in an AC Circuit MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 17

Resistor in an AC Circuit

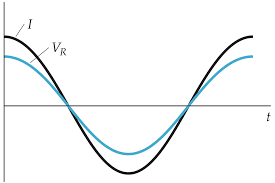
For the case of a resistor in an AC circuit the VR across the resistor is in phase with the current I through the resistor. In phase means that both waveforms peak at the same time. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 18

Resistor in an AC Circuit

22
p 2 2 p

P(t)= I (t)R = I cosωt R

P(t)= I RcosωtThe instantaneous power is a function of time. However, the average power per cycle is of more interest. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 19Inductors in an AC Circuit MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 20

Coils & Caps in an AC Circuit

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 21

Inductors in an AC Circuit

For the case of an inductor in an

AC circuit the VL across the

inductor is 90

0 ahead of the current

I through the inductor.

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 22

Inductors in an AC Circuit

L peak

p

L peak L peak

p L

LVπI = I sinωt = cosωt -2ωL

V VI = =ωL X

X =ωL

XL is the inductive reactance

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 23

Average Power - Inductors( )( )

L L peak p

L peak p

T avg L peak p 0 T

L peak p

avg 0 T

L peak p

avg 0

P(t)=V I = V cosωt I sinωt

P(t)=V I cosωt sinωt

1

P = V I cosωt sinωtdtT

V IP = cosωt sinωtdtT

V IP = sin2ωtdt = 02TInductors don't dissipate energy, they store energy. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 24

Average Power - Inductors

Inductors don't dissipate energy, they

store energy.

The voltage and the current are out of

phase by 90o.

As we saw with Work, energy

changed only when a portion of the force was in the direction of the displacement.

In electrical circuits energy is

dissipated only if a portion of the voltage is in phase with the current. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 25Capacitors in an AC Circuit MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 26

Capacitors in an AC Circuit

C p C p

C C p p

p p p pV = cosωt =V cosωt

Q =V C =V Ccosωt = Q cosωt

dQI = = -ωQ sinωt = -I sinωtdt

I = -ωQ sinωt = I cosωt +2

For the case of a capacitor in an

AC circuit the VC across the

capacitor is 90

0 behind the current

I on the capacitor.

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 27

Capacitors in an AC Circuit

Cp Cp p p Cp C

CV VI =ωQ =ωCV = =1XωC

1X =ωC

XC is the capacitive reactance.

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 28Electrical Transformers MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 29

Electrical Transformers

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 30

Electrical Transformers

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 31 MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 32

Electrical Transformers

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 33

Electrical Transformers

Both coils see the same magnetic flux and the cross sectional areas are the same 0

0 1 1 0 2 2

1 1 2 2

1 2 1 2 2 1 2 2 1 2 1 1

B = μnI

μn I =μn I

n I = n I nI = In

NI n NL= = =NI n N

L MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 34

Electrical Transformers

Conservation of Energy

Primary Power = Secondary Power

in 1 out 2 out 1 2 in 2 1 2 out in

1V I =V I

V

I N= =V I N

NV = VN

Induced voltage/loop

More loops => more voltage

Voltage steps up but the current

steps down. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 35LC and RLC Circuits Without a

Generator

MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 36

LC Circuit - No Generator

To start this circuit some energy must be placed in it since there is no battery to drive the circuit. We will do that by placing a charge on the capacitor Since there is no resistor in the circuit and the resistance of the coil is assumed to be zero there will not be any losses. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 37

LC Circuit - No Generator

Apply Kirchhoff's rule

2 2 2 2

RdI QL + = 0dt C

dQSince I =dt d Q QL + = 0dt C d Q 1= - Qdt LC

1ω=LC

This is the harmonic

oscillator equation MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 38

LC Circuit - No Generator

p p p

Q(t)= Q cos

ωt dQI(t)= = -ωQ sin

ωtdtπ

I(t)= -

ωQ cos

ωt +2

The circuit will oscillate at the frequency

ωR. Energy will flow back and forth

from the capacitor (electric energy) to the inductor (magnetic energy). MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 39

RLC Circuit - No Generator

Like the LC circuit some energy must initially be placed in this circuit since there is no battery to drive the circuit. Again we will do this by placing a charge on the capacitor Since there is a resistor in the circuit now there will be losses as the energy passes through the resistor. MFMcGraw-PHY 2426 Chap31-AC Circuits-Revised: 6/24/2012 40

RLC Circuit - No Generator

Apply Kirchhoff's rule

2

2dI Q dQL + IR+ = 0 ; I =dt C dt

d Q dQ 1L + R + Q = 0dt dt C "ma" term

Damping term - friction

Restoring force "kx"

quotesdbs_dbs7.pdfusesText_13

[PDF] ac current

[PDF] ac frequency us

[PDF] ac tonnage calculation formula

[PDF] ac unit calculator

[PDF] ac2o dmap mechanism

[PDF] aca american cycling association

[PDF] aca certification accounting

[PDF] aca certification apple

[PDF] aca certification corrections

[PDF] aca certification cost

[PDF] aca certification courses

[PDF] aca certification exam

[PDF] aca certification phlebotomy

[PDF] aca code of ethics

[PDF] aca code of ethics pdf