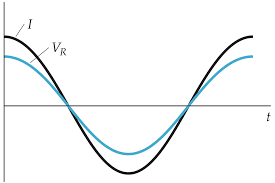
 Ch31-AC Circuits.pdf
Ch31-AC Circuits.pdf
• RLC Circuit - Solution via Complex Numbers. • RLC Circuit - Example The use of complex numbers simplifies the lead-lag nature of the voltage and current in ...
 Practice Problems - Chapter 33 Alternating Current Circuits
Practice Problems - Chapter 33 Alternating Current Circuits
0.34 A. Page 2. 2 CHAPTER 33. 20. An RLC series circuit has R = 100 ohms C = 25 µF
 QUESTION BANK WITH ANSWERS
QUESTION BANK WITH ANSWERS
Determine the power factor of a RLC series circuit with R=5ohm XL=8ohm and XC=12ohm. (JUNE
 ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
Example Problems: 1) Find the Req for the circuit shown in below figure. fig(a). Solution: To get Req we combine resistors in series and in parallel. The 6 ohms
 AC Electrical Circuit Analysis - A Practical Approach James M. Fiore
AC Electrical Circuit Analysis - A Practical Approach James M. Fiore
Apr 22 2021 D: Answers to Selected Odd-Numbered Problems . . . . 408. E: Questions for Selected Odd Answers . . . . . 422. 9. Page 10. 1 Fundamentals. 1.0 ...
 BEE-402; UNIT-I MESH AND NODAL ANALYSIS of AC circuits
BEE-402; UNIT-I MESH AND NODAL ANALYSIS of AC circuits
Assume o=10° radians per second. == Solution 2: Convert the circuit to the phasor domain. Solve the problem using circuit techniques (nodal analysis mesh ...
 0.1. Single Phase AC circuit - JNNCE ECE Manjunath
0.1. Single Phase AC circuit - JNNCE ECE Manjunath
Problems on Three phase AC circuits. 0.4 Problems on Three phase AC circuits Calculate power power factor and current in the circuit. Solution: Z = E. I. =.
 ee301 – phasors complex numbers in ac and impedance
ee301 – phasors complex numbers in ac and impedance
Sep 22 2016 Solving AC circuit problems is greatly simplified through the use of the phasor transform. ... Solution: Example: Given: I1 = 20 sin (ω t) mA. I2 ...
 ELECTRICAL CIRCUIT ANALYSIS Lecture Notes Prepared By S
ELECTRICAL CIRCUIT ANALYSIS Lecture Notes Prepared By S
A.C TRANSIENT ANALYSIS: Transient response of R-L R-C
 DC NETWORK THEOREMS
DC NETWORK THEOREMS
This method which is particularly well-suited to coupled circuit solutions employs a system of ** Or impedance in the case of a.c. circuits. *. After the ...
 Ch31-AC Circuits.pdf
Ch31-AC Circuits.pdf
Alternating Current Circuits. • Alternating Current - AC Circuits: Resistor; Inductor; Capacitor ... RLC Circuit - Solution via Complex Numbers.
 BASIC ELECTRICAL ENGINEERING
BASIC ELECTRICAL ENGINEERING
In order to analyze AC circuit it is necessary to represent multi-dimensional quantities. In Problem: Find impedance Zin of below circuit. Solution: ...
 SINGLE PHASE AC CIRCUITS
SINGLE PHASE AC CIRCUITS
Phasor Algebra for a pure resistive circuit. Problem 2. An ac circuit consists of a pure resistance of 10 and is connected to an ac supply of 230 V 50 Hz.
 ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
Example Problems: 1) Find the Req for the circuit shown in below figure. fig(a). Solution: To get Req we combine resistors in series and in parallel.
 CBSE NCERT Solutions for Class 12 Physics Chapter 7
CBSE NCERT Solutions for Class 12 Physics Chapter 7
(b) The rms value of current in an ac circuit is 10 A. What is the peak current? Solution: (a). Given. Peak voltage
 Practice Problems - Chapter 33 Alternating Current Circuits
Practice Problems - Chapter 33 Alternating Current Circuits
0.34 A. Page 2. 2 CHAPTER 33. 20. An RLC series circuit has R = 100 ohms C = 25 µF
 Series and parallel AC circuits This worksheet and all related files
Series and parallel AC circuits This worksheet and all related files
A student measures voltage drops in an AC circuit using three voltmeters and arrives on this problem you realize that neither of the answers proposed.
 A-C Circuit Analysis - Alexander Schure.pdf
A-C Circuit Analysis - Alexander Schure.pdf
A-C CIRCUIT. ANALYSIS publication carefully selected problems afford the reader more profitable in- ... Solution. f = 1/t = l;.0025 = 400 cycles.
 Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis
E1.1 Circuit Analysis. Problem Sheet 2 - Solutions. Note: In many of the solutions below I have written the voltage at node X as the variable X instead of.
 AC Electrical Circuit Analysis - A Practical Approach James M. Fiore
AC Electrical Circuit Analysis - A Practical Approach James M. Fiore
22?/04?/2021 This AC Electrical Circuit Analysis by James M. Fiore is copyrighted under the terms of ... D: Answers to Selected Odd-Numbered Problems.
Series and parallel AC circuits
This worksheet and all related files are licensed under the Creative Commons Attribution License,version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/, or send a
letter to Creative Commons, 559 Nathan Abbott Way, Stanford, California 94305, USA. The terms andconditions of this license allow for free copying, distribution, and/or modification of all licensed works by
the general public. Resources and methods for learning about these subjects (list a few here, in preparationfor your research): 1Questions
Question 1
Doorbell circuits connect a small lamp in parallel with the doorbell pushbutton so that there is light
at the button when it isnotbeing pressed. The lamp"s filament resistance is such that there is not enough
current going through it to energize the solenoid coil when lit, which means the doorbell will ring only when
the pushbutton switch shorts past the lamp:60 Hz18 V
Doorbell switch
Solenoid
Lamp Suppose that such a doorbell circuit suddenly stops working one day, and the home owner assumes thepower source has quit since the bell will not ring when the button is pressed and the lamp never lights.
Although a dead power source is certainly possible, it is not the only possibility. Identify another possible
failure in this circuit which would result in no doorbell action (no sound) and no light at the lamp.
file 03447Question 2
Calculate the total impedance offered by these two inductors to a sinusoidal signal with a frequency of
60 Hz:
L1 L2750 mH
350 mH
Ztotal @ 60 Hz = ???
Show your work using two different problem-solving strategies: •Calculating total inductance (Ltotal) first, then total impedance (Ztotal). •Calculating individual impedances first (ZL1andZL2), then total impedance (Ztotal). Do these two strategies yield the same total impedance value? Why or why not? file 01832 2Question 3
Calculate the total impedance offered by these two capacitors to a sinusoidal signal with a frequency of
3 kHz:
C1C20.01 μF
0.022 μFZtotal @ 3 kHz = ???
Show your work using two different problem-solving strategies: •Calculating total capacitance (Ctotal) first, then total impedance (Ztotal). •Calculating individual impedances first (ZC1andZC2), then total impedance (Ztotal). Do these two strategies yield the same total impedance value? Why or why not? file 01834Question 4
Write an equation that solves for the impedance of this series circuit. The equation need not solve for
the phase angle between voltage and current, but merely provide a scalar figure for impedance (in ohms):
Ztotal = ???
R X file 00850 3Question 5
Write an equation that solves for the impedance of this series circuit. The equation need not solve for
the phase angle between voltage and current, but merely provide a scalar figure for impedance (in ohms):
Ztotal = ???
R X file 01844 4Question 6
A student measures voltage drops in an AC circuit using three voltmeters and arrives at the following
measurements: COMA V VA A OFF COMA V VA A OFF COMA V VA A OFF Upon viewing these measurements, the student becomes very perplexed. Aren"t voltage drops supposedtoaddin series, just as in DC circuits? Why, then, is the total voltage in this circuit only 10.8 volts and not
15.74 volts? How is it possible for the total voltage in an AC circuit to be substantially less than the simple
sum of the components" voltage drops?Another student, trying to be helpful, suggests that the answer to this question might have something
to do with RMS versus peak measurements. A third student disagrees, proposing instead that at least one
of the meters is badly out of calibration and thus not reading correctly.When you are asked for your thoughts on this problem, you realize that neither of the answers proposed
thus far are correct. Explain the real reason for the "discrepancy" in voltagemeasurements, and also explain
how you could experimentally disprove the other answers (RMS vs. peak, and bad calibration). file 01566 5Question 7
Draw a phasor diagram showing the trigonometric relationship between resistance, reactance, and impedance in this series circuit:5 V RMS
350 Hz2.2 kΩ
680 mH
R L Show mathematically how the resistance and reactance combine in series to produce a total impedance(scalar quantities, all). Then, show how to analyze this same circuit using complex numbers: regarding
component as having its own impedance, demonstrating mathematically how these impedances add up to comprise the total impedance (in both polar and rectangular forms). file 01827Question 8
Calculate the magnitude and phase shift of the current through this inductor, taking into consideration
its intrinsic winding resistance:Vin10 VAC
Inductor
1.5 H65 Ω
135 Hz
file 00639 6Question 9
Calculate the necessary size of the capacitor to give this circuit a total impedance(Ztotal) of 4 kΩ, at a
power supply frequency of 100 Hz:100 Hz2k2
C = ???
file 04042Question 10
Draw a phasor diagram showing the trigonometric relationship between resistance, reactance, and impedance in this series circuit:5 V RMS
350 Hz2.2 kΩ
R C0.22 μF
Show mathematically how the resistance and reactance combine in series to produce a total impedance(scalar quantities, all). Then, show how to analyze this same circuit using complex numbers: regarding each
of the component as having its own impedance, demonstrating mathematically how these impedances add up to comprise the total impedance (in both polar and rectangular forms). file 01828 7Question 11
Which component, the resistor or the capacitor, will drop more voltage inthis circuit?5k1725 Hz47n
Also, calculate the total impedance (Ztotal) of this circuit, expressing it in both rectangular and polar
forms. file 03784Question 12
Calculate the total impedance of this series LR circuit and then calculate the totalcircuit current:3 kHz34 V RMS250m
5k1 Also, draw a phasor diagram showing how the individual component impedances relate to the total impedance. file 02103 8Question 13
A quantity sometimes used in DC circuits isconductance, symbolized by the letterG. Conductance is the reciprocal of resistance (G=1R), and it is measured in the unit of siemens.
Expressing the values of resistors in terms of conductance instead of resistance hascertain benefits in
parallel circuits. Whereas resistances (R) add in series and "diminish" in parallel (with a somewhat complex
equation), conductances (G) add in parallel and "diminish" in series. Thus, doing the math for series circuits
is easier using resistance and doing math for parallel circuits is easier using conductance: R1 R 2 R 3R1R2R3
Rtotal = R1 + R2 + R3Gtotal = G1 + G2 + G3
Rtotal =1
R1+1+1R2R31
Gtotal =1+1+1
1 G 1G2G3In AC circuits, we also have reciprocal quantities to reactance (X) and impedance (Z). The reciprocal
of reactance is calledsusceptance(B=1 X), and the reciprocal of impedance is calledadmittance(Y=1Z). Like conductance, both these reciprocal quantities are measured in units of siemens. Write an equation that solves for the admittance (Y) of this parallel circuit. The equation need notsolve for the phase angle between voltage and current, but merely provide a scalarfigure for admittance (in
siemens): G BY total = ??? file 00853 9Question 14
A quantity sometimes used in DC circuits isconductance, symbolized by the letterG. Conductance is the reciprocal of resistance (G=1R), and it is measured in the unit of siemens.
Expressing the values of resistors in terms of conductance instead of resistance hascertain benefits in
parallel circuits. Whereas resistances (R) add in series and "diminish" in parallel (with a somewhat complex
equation), conductances (G) add in parallel and "diminish" in series. Thus, doing the math for series circuits
is easier using resistance and doing math for parallel circuits is easier using conductance: R1 R 2 R 3R1R2R3
Rtotal = R1 + R2 + R3Gtotal = G1 + G2 + G3
Rtotal =1
R1+1+1R2R31
Gtotal =1+1+1
1 G 1G2G3In AC circuits, we also have reciprocal quantities to reactance (X) and impedance (Z). The reciprocal
of reactance is calledsusceptance(B=1 X), and the reciprocal of impedance is calledadmittance(Y=1Z). Like conductance, both these reciprocal quantities are measured in units of siemens. Write an equation that solves for the admittance (Y) of this parallel circuit. The equation need notsolve for the phase angle between voltage and current, but merely provide a scalarfigure for admittance (in
siemens): G BY total = ??? file 01845 10Question 15
Calculate the total impedance offered by these three resistors to a sinusoidal signal with a frequency of
10 kHz:
•R1= 3.3 kΩ •R2= 10 kΩ •R3= 5 kΩ R1 R2 R3Ztotal @ 10 kHz = ???Surface-mount resistors on a printed-circuit board State your answer in the form of a scalar number (not complex), but calculate it using two different strategies: •Calculate total resistance (Rtotal) first, then total impedance (Ztotal). •Calculate individual admittances first (YR1,YR2, andYR3), then total impedance (Ztotal). file 01836Question 16
Calculate the total impedance offered by these three capacitors to a sinusoidal signal with a frequency
of 4 kHz: •C1= 0.1μF •C2= 0.047μF •C3= 0.033μF on a printed-circuit boardC1 C2 C3
Ztotal @ 4 kHz = ???Surface-mount capacitors
State your answer in the form of a scalar number (not complex), but calculate it using two different strategies: •Calculate total capacitance (Ctotal) first, then total impedance (Ztotal). •Calculate individual admittances first (YC1,YC2, andYC3), then total impedance (Ztotal). file 01846 11Question 17
Calculate the total impedance of these parallel-connected components, expressing it inpolar form (magnitude and phase angle): on a printed-circuit boardC1 R1Surface-mount components
33nZtotal @ 7.9 kHz = ???510
Also, draw an admittance triangle for this circuit. file 02108Question 18
Calculate the total impedance of this LR circuit, once using nothing but scalar numbers, and again using complex numbers: R1L150m1k5
Z total @ 8 kHz = ??? file 01837 12Question 19
Calculate the total impedance offered by these two inductors to a sinusoidal signal with a frequency of
120 Hz:
L1 L2Ztotal @ 120 Hz = ???
500 mH
1.8 H Show your work using three different problem-solving strategies: •Calculating total inductance (Ltotal) first, then total impedance (Ztotal).•Calculating individual admittances first (YL1andYL2), then total admittance (Ytotal), then total
impedance (Ztotal).•Using complex numbers: calculating individual impedances first (ZL1andZL2), then total impedance
(Ztotal). Do these two strategies yield the same total impedance value? Why or why not? file 01833Question 20
Calculate the total impedance of this RC circuit, once using nothing but scalar numbers, and again using complex numbers: R1 C1Ztotal @ 400 Hz = ???
7.9 kΩ0.047 μF
file 01838 13Question 21
Calculate the total impedance offered by these two capacitors to a sinusoidal signal with a frequency of
900 Hz:
C1C2Ztotal @ 900 Hz = ???0.33 μF
0.1 μF
Show your work using three different problem-solving strategies: •Calculating total capacitance (Ctotal) first, then total impedance (Ztotal).•Calculating individual admittances first (YC1andYC2), then total admittance (Ytotal), then total
impedance (Ztotal).•Using complex numbers: calculating individual impedances first (ZC1andZC2), then total impedance
(Ztotal). Do these two strategies yield the same total impedance value? Why or why not? file 01835Question 22
Calculate the total impedance for these two 100 mH inductors at 2.3 kHz, and drawa phasor diagram showing circuit impedances (Ztotal,R, andX): L1 L2 100m100m
Ztotal @ 2.3 kHz = ???
Now, re-calculate impedance and re-draw the phasor impedance diagram supposing the second inductor is replaced by a 1.5 kΩ resistor: L1100mZtotal @ 2.3 kHz = ???
R1 1k5 file 02080 14Question 23
Calculate the total impedance for these two 100 mH inductors at 2.3 kHz, and drawa phasor diagram showing circuit admittances (Ytotal,G, andB):L1L2Ztotal @ 2.3 kHz = ???100m 100m
Now, re-calculate impedance and re-draw the phasor admittance diagram supposing the second inductor is replaced by a 1.5 kΩ resistor:L1Ztotal @ 2.3 kHz = ???100m
1k5 R1 file 02079Question 24
Calculate the individual currents through the inductor and through the resistor, the total current, and
the total circuit impedance:3 kHz250m
5k12.5 V RMS
Also, draw a phasor diagram showing how the individual component currents relate to the total current.
file 02104 15Question 25
Due to the effects of a changing electric field on the dielectric of a capacitor, some energyis dissipated
in capacitors subjected to AC. Generally, this is not very much, but it is there. This dissipative behavior is
typically modeled as a series-connected resistance:Equivalent Series Resistance (ESR)
Ideal capacitorReal
capacitorCalculate the magnitude and phase shift of the current through this capacitor, taking into consideration
its equivalent series resistance (ESR):Vin10 VAC
0.22 μF5 ΩCapacitor
270 Hz
Compare this against the magnitude and phase shift of the current for an ideal 0.22μF capacitor. file 01847Question 26
Solve for all voltages and currents in this series LR circuit:175 mH
15 V RMS
1 kHz710 Ω
file 01830 16Question 27
Solve for all voltages and currents in this series LR circuit, and also calculate the phase angle of the
total impedance:5 kΩ
24 V RMS50 Hz10.3 H
file 01831Question 28
Solve for all voltages and currents in this series RC circuit:15 V RMS
1 kHz0.01 μF
4.7 kΩ
file 01848Question 29
Solve for all voltages and currents in this series RC circuit, and also calculate the phase angle of the
total impedance:48 V peak30 Hz3k3220n
file 01849 17Question 30
One way to vary the amount of power delivered to a resistive AC load is by varying another resistance
connected in series: RloadRseries
A problem with this power control strategy is that power is wasted in the series resistance (I2Rseries).
A different strategy for controlling power is shown here, using a seriesinductancerather than resistance:
RloadLseries
Explain why the latter circuit is more power-efficient than the former, and draw aphasor diagram showing how changes inLseriesaffectZtotal. file 01829 18Question 31
A technician needs to know the value of a capacitor, but does not have a capacitance meter nearby. In
lieu of this, the technician sets up the following circuit to measure capacitance:A B Alt Chop Add
Volts/Div A
Volts/Div BDC Gnd AC
DC Gnd AC
InvertIntensityFocus
Position
PositionPosition
OffBeam find
Line Ext.A B AC DC Norm AutoSingleSlope
Level Reset X-YHoldoff
LF Rej
HF Rej
Triggering
AltExt. input
Cal 1 VGndTrace rot.
Sec/Div
0.50.20.1
1 10 5220 50 m
20 m 10 m 5 m 2 m 0.5
0.20.1
1 10 5220 50 m
20 m 10 m 5 m 2 m
1 m5 m
25 m100 m
500 m
2.5
1250 μ50 μ10 μ
2.5 μ
0.5 μ
0.1 μ
0.025 μoff
HzFUNCTION GENERATOR
1 101001k10k100k1M
outputDCfinecoarse CxR You happen to walk by this technician"s workbench and ask, "How does this measurement setup work?"The technician responds, "You connect a resistor of known value (R) in series with the capacitor of unknown
quotesdbs_dbs12.pdfusesText_18[PDF] ac frequency us
[PDF] ac tonnage calculation formula
[PDF] ac unit calculator
[PDF] ac2o dmap mechanism
[PDF] aca american cycling association
[PDF] aca certification accounting
[PDF] aca certification apple
[PDF] aca certification corrections
[PDF] aca certification cost
[PDF] aca certification courses
[PDF] aca certification exam
[PDF] aca certification phlebotomy
[PDF] aca code of ethics
[PDF] aca code of ethics pdf
