 Droite de Henry.pdf
Droite de Henry.pdf
(on note Φ la fonction de répartition de la loi normale centrée réduite). Pour chaque valeur xi de la variable X on peut (à l'aide d'une table de la
 Tests de normalité dune population
Tests de normalité dune population
⊳ Décision grâce au test de Henry. ⊳ Décision grâce au test de Lilliefors Nuage de points proches d'une droite : on accepte la normalité de la population.
 Comment construire un diagramme de Henry avec Excel et
Comment construire un diagramme de Henry avec Excel et
Le diagramme de Henry (ou « droite de Henry ») permet d'apprécier l'adéquation d'une distribution observée à la loi de Gauss.
 TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
Graphiquement en utilisant la méthode de la droite de Henry. C - POUR VOUS Les données de l'exercice A1 restent valables mais maintenant on ne répare plus une.
 Chapitre 4 : Régression linéaire
Chapitre 4 : Régression linéaire
Ce type de graphique est appelé droite de Henry. Si les résidus ne sont pas normalement distribués ils vont s'écarter de la droite. Analyse de l
 Vidéo 3 Exercice Corrigé Alain HENRY
Vidéo 3 Exercice Corrigé Alain HENRY
Vidéo 3. Exercice Corrigé. Alain HENRY. Page 2. Vidéo 3. Exercice Corrigé. Alain HENRY. Page 3. Vidéo 3. Exercice Corrigé. Alain HENRY. Page 4. Vidéo 3.
 Cours de Statistiques inférentielles
Cours de Statistiques inférentielles
La droite de Henry est une méthode pour visualiser les chances qu'a une Ref : Statistique exercices corrigés
 TD 3 : ANOVA à un facteur
TD 3 : ANOVA à un facteur
1 avr. 2010 Exercice 1 : On souhaite étudier les effets de trois ... c) Regarder la normalité des résidus à l'aide de la droite de Henry des résidus.
 Untitled
Untitled
Exercices et Corrigés. Par Abdelwaheb SARI AHMED. Maître de Conférences Associé droite de Henry et la courbe expérimentale) tracer les courbes enveloppes.
 55 Exercice 6 AJUSTEMENT DES PRECIPITATIONS ANNUELLES
55 Exercice 6 AJUSTEMENT DES PRECIPITATIONS ANNUELLES
Corrigé : Quelle que soit la série du cumul est l'équation de la droite de Henry ajustant ... L'examen graphique ne peut suffire il faut pouvoir tester.
 Droite de Henry.pdf
Droite de Henry.pdf
(on note ? la fonction de répartition de la loi normale centrée réduite). Pour chaque valeur xi de la variable X on peut (à l'aide d'une table de la
 Tests de normalité dune population
Tests de normalité dune population
Tests de Henry et Lilliefors. A. Claeys 3 Test de Henry. ... On étire irrégulièrement l'axe des ordonnées pour rendre la courbe droite.
 TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
Graphiquement en utilisant la méthode de la droite de Henry. C - POUR VOUS TESTER Sujet de l'étude ... Exercices d'application directe du cours.
 INTERET DE LUTILISATION DE LA DROITE DE HENRY EN
INTERET DE LUTILISATION DE LA DROITE DE HENRY EN
On connaît donc* sans correction le nombre d'impulsions correspondant à un certain nombre de canaux. Le graphique de Henry montre à quel pourcentage 11.
 Cours de Statistiques inférentielles
Cours de Statistiques inférentielles
La droite de Henry est une méthode pour visualiser les chances qu'a une distribution Ref : Statistique exercices corrigés
 Chapitre 4 : Régression linéaire
Chapitre 4 : Régression linéaire
Ce type de graphique est appelé droite de Henry. Si les résidus ne sont pas normalement distribués ils vont s'écarter de la droite. Analyse de l'
 No Slide Title
No Slide Title
Les paramètres influents. Exercice de la table Tracer la droite de Henry pour cet échantillon ... Identifier et corriger la ou les causes spéciales.
 Probabilités et statistiques Travaux pratiques avec Matlab
Probabilités et statistiques Travaux pratiques avec Matlab
division à gauche et la division à droite et enfin l'élévation à une puissance. Exercice 1.4 Tester et interpréter les commandes suivantes.
 Sur ladéquation `a une loi de probabilité avec
Sur ladéquation `a une loi de probabilité avec
de la "droite diagonale" d'équation : y = x. ? Cas d'une loi normale : méthode du QQ plot (QQ norm) avec droite de Henry : Soit zp le quantile.
 Droite de Henry
Droite de Henry
Droite de Henry La droite de Henry est une méthode pour visualiser les chances qu'a une distribution d'être gaussienne Elle permet de lire rapidement la moyenne et l'écart type d'une telle distribution Principe Si X est une variable gaussienne de moyenne et de variance ?2 et si N est une variable de loi normale centrée réduite on a les
Pourquoi utiliser la droite de Henry ?
En tant qu’outil directement opérationnel, la droite de Henry est notamment utilisée en management de la qualité. Et sinon ? Dans le cadre d’une régression ou d’un lissage, on peut visualiser la droite de Henry des résidus afin de s’assurer que leur distribution ne s’éloigne pas trop d’une loi normale.
Comment convertir une loi en droite ?
L’intérêt est alors de comparer cette droite avec la fonction de répartition de la loi normale, elle-même transformée en droite, soit grâce au secours d’un papier gausso-arithmétique, soit grâce à votre logiciel qui s’occupe de ces petites transformations.
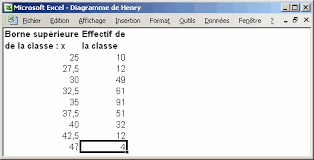
Comment obtenir une droite de distribution ?
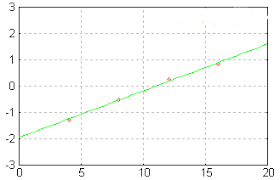
Si la distribution suit une loi normale on doit obtenir une droite en portant les extrémités de classe en abscisse et les valeurs de ? en ordonnée. On constate que la distribution observée peut être assimilée à une loi normale car la linéarité est satisfaisante (hormis les 2 points supérieurs qui sont dus à des classes de même fréquence).
Université de Caen
Sur l"ad
´equation`a une loi de probabilit´e avecChristophe Chesneau https://chesneau.users.lmno.cnrs.fr/Caen, le 10 Avril 2018Table des matières
Table des matières
1 Point de départ5
2 Analyses graphiques 7
3 Tests statistiques d"adéquation à une loi 25
3.1 Test du Chi-deux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
253.2 Test de Kolmogorov-Smirnov . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
323.3 Test de Shapiro-Wilk . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
334 Exercices37
5 Solutions43
Note L"objectif de ce document est de présenter les principaux outils statistiques et commandesR utilisés pour juger de l"adéquation de la distribution des valeurs d"un caractère à une loi
de probabilité.Contact :christophe.chesneau@gmail.com
Bonne lecture!C. Chesneau3
1 Point de départ
1 Point de départ
On observe la valeur d"un caractèreXpour chacun desnindividus d"un échantillon. Ces observa-tions constituent les données :x1;:::;xn. On modélise alorsXcomme unevar(en gardant la notation
Xpar convention). SoitLune loi de probabilité étant possiblement en adéquation avec la loi inconnue
deX. La problématique est la suivante : Est-ce que ces données nous permettent d"affirmer queXne suit pas la loiL(avec un faible risque de se tromper)? Pour répondre à cette question, on distingue deux approches complémentaires :Analyses graphiques.
Tests statistiques adaptées reposant sur les hypothèses : H0: "Xsuit la loiL" contreH1: "Xne suit pas la loiL".
Dans ce document, nous mettons en oeuvre ces tests en utilisant la p-valeur.La p-valeur est le plus petit réel2]0;1[calculé à partir des données tel que l"on puisse se
permettre de rejeterH0au risque100%. Autrement écrit, la p-valeur est une estimation ponctuelle de la probabilité critique de se tromper en rejetantH0alors queH0est vraie. Les logiciels actuels travaillent principalement avec cette p-valeur.C. Chesneau52 Analyses graphiques
2 Analyses graphiques
Cas de caractères qualitatifs ou quantitatifs "discrets"SoitXun caractère non chiffré (qualitatif) ou chiffré (quantitatif) prenant un ensemble dénom-
brable de valeurs (possiblement infini). L"analyse graphique la plus pertinente pour juger de l"adéqua-
tion de la loi deXavecLrepose sur le schéma suivant : On trace le barplot des fréquences correspondantes aux données.On superpose les valeurs de la "densité" associée à la loiLen estimant éventuellement les
paramètres inconnus de celle-ci.Exemple
Exemple 1.
On souhait esa voirsi les en tréesà l"hôpital p ourune certaine maladie son tréparties au
hasard dans l"année ou bien si certains mois sont plus propices à la maladie. On examine le mois
d"entrée d"un échantillon de120porteurs de la maladie étudiée. Les résultats sont :Mois d"entrée 1 2 3 4 5 6 7 8 9 10 11 12
Nombre d"entrées 18 16 8 10 6 4 4 9 11 10 12 12Peut-on affirmer que "les entrées ne se font pas au hasard dans l"année" (donc que "certains mois
sont plus propices à la maladie")?Solution 1.
Soit Xlavarégale au mois d"entrée à l"hôpital d"un porteur de la maladie. Par l"énoncé,
on observe la valeur deXsur chacun desnindividus (porteurs de la maladie) d"un échantillon avec n= 120:(x1;:::;xn)(avecxi2 f1;:::;12g). On forme alors un vecteur des effectifs (n1;n2;:::;n12) = (18;16;:::;12).Dire que les entrées se font au hasard dans l"année signifie queXsuit la loi uniformeU(f1;:::;12g):
P(X=i) =112
; i2 f1;:::;12g:La problématique est la suivante : est-ce que ces données nous permettent d"affirmer queXne suit pas
la loiL=U(f1;:::;12g)?C. Chesneau72 Analyses graphiques
Pour touti2 f1;:::;12g, une estimation (ponctuelle) deP(X=i)est la fréquenceni=n.Ainsi, pour une analyse graphique, on peut
tracer le barplot des fréquences correspondantes aux données, superposer les valeurs de la "densité" associée à la loi uniformeU(f1;:::;12g).On propose les commandes :
nb = c(18, 16, 8, 10, 6, 4, 4, 9, 11, 10, 12, 12) bar = barplot(nb / 120, col = "white") points(bar, rep(1 / 12, 12), type = "h")Cela renvoie : Les différences observées laissent penser queXne suit pas une loi uniforme.C. Chesneau82 Analyses graphiques
Exemple 2.
Dans un v erger,on étudie le comp ortementdes insect esquand ceux-ci attaquen tles fruits.SoitXle caractère qui dénombre le nombre d"attaques d"insectes sur un fruit pris au hasard. Une étude
statistique antérieure montre que, si les attaques se font de façon indépendante les unes des autres, on
peut modéliserXcomme unevarsuivant une loi de PoissonP()avecinconnu. On considère un échantillon de300fruits et on compte le nombre d"attaques sur le fruit. Les résultats sont :Nombre d"attaques 0 1 2 3 4 5 6 7 Nombre de fruits attaqués 60 105 65 47 15 4 3 1 Peut-on dire que le comportement des insectes est grégaire?(on dit que le comportement desinsectes est grégaire quand chacun d"entre eux a tendance à se comporter comme le voisin et à attaquer
le même fruit; dans ce cas,Xne suit pas une loi de Poisson).Solution 2.
P arl"énoncé, on observ ela v aleurde Xsur chacun desnindividus (fruits) d"un échantillon avecn= 300:(x1;:::;xn)(avecxi2N). On forme alors un vecteur des effectifs (n1;n2;:::;n8) = (60;105;:::;1). Dire queXsuit la loi de PoissonP(), avecinconnu, signifie que :P(X=i) =eii!; i2N:
Pour évaluer la loi de Poisson la plus adaptée à notre contexte, il faut estimerà l"aide des données.
CommeE(X) =, la méthode des moments nous assure qu"une estimation deestx=1n n X i=1x i=060 + 1105 + 265 + 347 + 415 + 54 + 63 + 71300 = 1:603333:Ainsi, la problématique est la suivante : est-ce que ces données nous permettent d"affirmer queXne
suit pas la loiL=P(1:603333)? Pour touti2 f0;:::;7g, une estimation deP(X=i)est la fréquenceni+1=net une estimation deP(X8) = 1P(X7)est :
18X i=1n in :C. Chesneau92 Analyses graphiques
Ainsi, pour une analyse graphique, on peut
tracer le barplot des fréquences correspondantes aux données, superposer les valeurs de la "densité" associée à la loi de poissonP(1:603333).On propose les commandes :
nb = c(60, 105, 65, 47, 15, 4, 3, 1, 0) bar = barplot(nb / 300, col = "white") lambda = sum((0:8) * nb) / 300 prob = c(dpois(0:7, lambda), 1 - ppois(7, lambda)) points(bar, prob, type = "h")Cela renvoie :Les différences observées laissent penser queXsuit une loi de Poisson, remettant ainsi en cause le
comportement grégaire des insectes.C. Chesneau102 Analyses graphiques
Cas de caractères quantitatifs "continus"
SoitXun caractère chiffré (quantitatif) prenant un ensemble indénombrable de valeurs. Les ana-
lyses graphiques possibles pour juger de l"adéquation de la loi deXavecLsont nombreuses. Les méthodes usuelles sont :Méthode de l"histogramme :On t racel"hi stogrammed esfréquenc escorresp ondantesau xdonnées.
Puis on superpose les valeurs de la "densité" associée à la loiLen estimant éventuellement les
paramètres inconnus de celle-ci.Méthode de la fonction de répartition :On trace le graphe de la fonction de r épartitionempirique
définie par : F n(x) =1n n X i=11 fxixg; x2R:Puis on superpose le graphe de la fonction de répartition associée à la loiLen estimant éven-
tuellement les paramètres inconnus de celle-ci.Méthode de l"approximation de la densité :On utilise une es timationde la densité inconn ue.Puis on
superpose les valeurs de la "densité" associée à la loiLen estimant éventuellement les paramètres
inconnus de celle-ci.Méthode du QQ plot (quantile-quantile plot) :Cette métho deconsiste en la comparaison des quan-
tiles empiriques et des quantiles théoriques. SoientF(x) =P(Xx)la fonction de répartition de Xetxple quantile d"ordrepdéfinie par :xp= inffx2R;F(x)pg. Soientx(1);x(2);:::;x(n)les données rangées par ordre croissant :x(1)< x(2)<< x(n). Alors on peut écrire la fonction
de répartition empirique comme F n(x) =1n n X i=11 fxixg=8 >>>:0six < x(1); kn six(k)x < x(k+1); k2 f1;:::;n1g;1sixx(n):
Soit(p1;p2;:::;pn)une suite strictement croissante denréels vérifiantpk2](k1)=n;k=n[, k2 f1;:::;ng, de sorte queinffx2R;Fn(x)pkg=x(k)pour toutk2 f1;:::;ng.C. Chesneau112 Analyses graphiques
On appelle QQ plot le nuage de pointsNdans le repère orthonormé(O;I;J)défini par :N=(xp1;x(1));(xp2;x(2));:::;(xpn;x(n)):
SiXsuit la loiL, les données font queFnest une bonne estimation deFet, a fortiori,x(k)doit bien estimerxpk:x(k)'xpkpour toutk2 f1;:::;ng; les points du nuageNdoivent être proche de la "droite diagonale" d"équation :y=x. Cas d"une loi normale : méthode du QQ plot (QQ norm) avec droite de Henry :Soit zple quantile d"ordrepd"unevarZsuivant la loi normale centrée réduiteN(0;1). Alors, siXsuit la loi normaleN(;2), le quantile d"ordrepdeXvérifie x p=+zp:Par conséquent, au lieu du QQ plot standard, on peut se contenter de construire le nuage de points
N dans le repère orthonormé(O;I;J)défini par :N=(zp1;x(1));(zp2;x(2));:::;(zpn;x(n)), avecpk=1n k12 ,k2 f1;:::;ng. SiXsuit la loiN(;2), alors les points du nuageN doivent être proche de la droite d"équation : y=x+sx; avecx=1n n X i=1x i; s=v uut1 n1n X i=1(xix)2:Cette droite est appelée droite de Henry.
Cas d"une loi normale : méthode de la boîte à moustaches :On fait la b oîteà moustac heasso ciée
aux données. SiXsuit une loi normale, la boîte doit être à peu près symétrique par rapport à
la médiane, idem pour les moustaches. D"autre part, il ne doit y avoir peu (ou pas) de points en dehors des moustaches.C. Chesneau122 Analyses graphiques
Exemples
Exemple 1.
On fait passer à 50adolescents le test psychologique de Rorschach. Les temps de passation en minutes du test sont :43 48 65 55 51 51 44 51 59 6245 53 55 55 49 34 52 69 45 54
59 36 36 29 52 59 41 58 54 55
72 53 52 49 57 42 70 58 42 53
57 68 40 65 54 49 32 56 50 59
On s"interroge pour savoir si lavarXqui à un adolescent associe son temps de passation au test suit ou non une loi normale.Solution 1.
P arl"énoncé, on ob servela v aleurde Xsur chacun desnindividus (adolescents) d"unéchantillon avecn= 50:(x1;:::;xn)(avecxi2R).
Dire queXsuit une loi normaleN(;2), avecetinconnus, signifie qu"elle possède la densité : f(x) =1p22e(x)222; x2R:Pour préciser la loi normaleN(;2)la plus adaptée à notre contexte, il faut estimeretà l"aide
des données. On estime alorsparx=1n n X i=1x i= 51:94 etpar s=v uut1 n1n X i=1(xix)2= 9:704638:Ainsi, la problématique est la suivante : est-ce que ces données nous permettent d"affirmer queXne
suit pas la loiL=N(51:94;9:7046382)?Nous allons faire une analyse graphique en utilisant les méthodes présentées précédemment.C. Chesneau13
2 Analyses graphiques
Méthode de l"histogramme :On propose les commandes : x = c(43, 48, 65, 55, 51, 51, 44, 51, 59, 62, 45, 53, 55, 55, 49, 34, 52,69, 45, 54, 59, 36, 36, 29, 52, 59, 41, 58, 54, 55, 72, 53, 52, 49, 57, 42,
70, 58, 42, 53, 57, 68, 40, 65, 54, 49, 32, 56, 50, 59)
hist(x, freq = FALSE, main = "Méthode de l"histogramme", ylab = "") curve(dnorm(x, 51.94, 9.704638), add = TRUE)Cela renvoie : Vu les différences observées, il est difficile de conclure.C. Chesneau14
2 Analyses graphiques
Méthode de la fonction de répartition :On propose les commandes : plot(ecdf(x), main = "Méthode de la fonction de répartition") curve(pnorm(x, 51.94, 9.704638), add = TRUE)Cela renvoie :quotesdbs_dbs33.pdfusesText_39[PDF] droite de henry pdf
[PDF] programmation linéaire exercices corrigés pdf
[PDF] programmation linéaire exercices corrigés
[PDF] programmation linéaire simplexe
[PDF] recherche opérationnelle programmation linéaire exercices corrigés pdf
[PDF] exercices recherche operationnelle
[PDF] theme astral chinois complet gratuit interpretation
[PDF] cours recherche opérationnelle methode de simplexe
[PDF] recherche opérationnelle simplexe exercices corrigés
[PDF] livre recherche opérationnelle pdf
[PDF] cours et exercices corrigés de recherche opérationnelle+pdf
[PDF] inpes
[PDF] methode boscher pdf download
[PDF] méthode boscher cahier de lecture pdf
