 Droite de Henry.pdf
Droite de Henry.pdf
(on note Φ la fonction de répartition de la loi normale centrée réduite). Pour chaque valeur xi de la variable X on peut (à l'aide d'une table de la
 Tests de normalité dune population
Tests de normalité dune population
⊳ Décision grâce au test de Henry. ⊳ Décision grâce au test de Lilliefors Nuage de points proches d'une droite : on accepte la normalité de la population.
 Comment construire un diagramme de Henry avec Excel et
Comment construire un diagramme de Henry avec Excel et
Le diagramme de Henry (ou « droite de Henry ») permet d'apprécier l'adéquation d'une distribution observée à la loi de Gauss.
 TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
Graphiquement en utilisant la méthode de la droite de Henry. C - POUR VOUS Les données de l'exercice A1 restent valables mais maintenant on ne répare plus une.
 Chapitre 4 : Régression linéaire
Chapitre 4 : Régression linéaire
Ce type de graphique est appelé droite de Henry. Si les résidus ne sont pas normalement distribués ils vont s'écarter de la droite. Analyse de l
 Vidéo 3 Exercice Corrigé Alain HENRY
Vidéo 3 Exercice Corrigé Alain HENRY
Vidéo 3. Exercice Corrigé. Alain HENRY. Page 2. Vidéo 3. Exercice Corrigé. Alain HENRY. Page 3. Vidéo 3. Exercice Corrigé. Alain HENRY. Page 4. Vidéo 3.
 Cours de Statistiques inférentielles
Cours de Statistiques inférentielles
La droite de Henry est une méthode pour visualiser les chances qu'a une Ref : Statistique exercices corrigés
 TD 3 : ANOVA à un facteur
TD 3 : ANOVA à un facteur
1 avr. 2010 Exercice 1 : On souhaite étudier les effets de trois ... c) Regarder la normalité des résidus à l'aide de la droite de Henry des résidus.
 Sur ladéquation `a une loi de probabilité avec
Sur ladéquation `a une loi de probabilité avec
Cette droite est appelée droite de Henry. ◦ Cas d'une loi normale : méthode Exercice 6. On mesure les durées de vie en heures de 7 appareils. Les ...
 Untitled
Untitled
Exercices et Corrigés. Par Abdelwaheb SARI AHMED. Maître de Conférences Associé droite de Henry et la courbe expérimentale) tracer les courbes enveloppes.
 55 Exercice 6 AJUSTEMENT DES PRECIPITATIONS ANNUELLES
55 Exercice 6 AJUSTEMENT DES PRECIPITATIONS ANNUELLES
Corrigé : Quelle que soit la série du cumul est l'équation de la droite de Henry ajustant ... L'examen graphique ne peut suffire il faut pouvoir tester.
 Droite de Henry.pdf
Droite de Henry.pdf
(on note ? la fonction de répartition de la loi normale centrée réduite). Pour chaque valeur xi de la variable X on peut (à l'aide d'une table de la
 Tests de normalité dune population
Tests de normalité dune population
Tests de Henry et Lilliefors. A. Claeys 3 Test de Henry. ... On étire irrégulièrement l'axe des ordonnées pour rendre la courbe droite.
 TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
TD n° 1 STATISTIQUE DESCRIPTIVE 7 13 8 10 9 12 10 8 9 10 6 14
Graphiquement en utilisant la méthode de la droite de Henry. C - POUR VOUS TESTER Sujet de l'étude ... Exercices d'application directe du cours.
 INTERET DE LUTILISATION DE LA DROITE DE HENRY EN
INTERET DE LUTILISATION DE LA DROITE DE HENRY EN
On connaît donc* sans correction le nombre d'impulsions correspondant à un certain nombre de canaux. Le graphique de Henry montre à quel pourcentage 11.
 Cours de Statistiques inférentielles
Cours de Statistiques inférentielles
La droite de Henry est une méthode pour visualiser les chances qu'a une distribution Ref : Statistique exercices corrigés
 Chapitre 4 : Régression linéaire
Chapitre 4 : Régression linéaire
Ce type de graphique est appelé droite de Henry. Si les résidus ne sont pas normalement distribués ils vont s'écarter de la droite. Analyse de l'
 No Slide Title
No Slide Title
Les paramètres influents. Exercice de la table Tracer la droite de Henry pour cet échantillon ... Identifier et corriger la ou les causes spéciales.
 Probabilités et statistiques Travaux pratiques avec Matlab
Probabilités et statistiques Travaux pratiques avec Matlab
division à gauche et la division à droite et enfin l'élévation à une puissance. Exercice 1.4 Tester et interpréter les commandes suivantes.
 Sur ladéquation `a une loi de probabilité avec
Sur ladéquation `a une loi de probabilité avec
de la "droite diagonale" d'équation : y = x. ? Cas d'une loi normale : méthode du QQ plot (QQ norm) avec droite de Henry : Soit zp le quantile.
 Droite de Henry
Droite de Henry
Droite de Henry La droite de Henry est une méthode pour visualiser les chances qu'a une distribution d'être gaussienne Elle permet de lire rapidement la moyenne et l'écart type d'une telle distribution Principe Si X est une variable gaussienne de moyenne et de variance ?2 et si N est une variable de loi normale centrée réduite on a les
Pourquoi utiliser la droite de Henry ?
En tant qu’outil directement opérationnel, la droite de Henry est notamment utilisée en management de la qualité. Et sinon ? Dans le cadre d’une régression ou d’un lissage, on peut visualiser la droite de Henry des résidus afin de s’assurer que leur distribution ne s’éloigne pas trop d’une loi normale.
Comment convertir une loi en droite ?
L’intérêt est alors de comparer cette droite avec la fonction de répartition de la loi normale, elle-même transformée en droite, soit grâce au secours d’un papier gausso-arithmétique, soit grâce à votre logiciel qui s’occupe de ces petites transformations.
Comment obtenir une droite de distribution ?
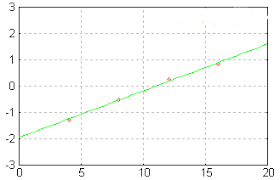
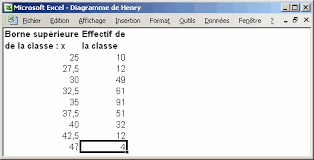
Si la distribution suit une loi normale on doit obtenir une droite en portant les extrémités de classe en abscisse et les valeurs de ? en ordonnée. On constate que la distribution observée peut être assimilée à une loi normale car la linéarité est satisfaisante (hormis les 2 points supérieurs qui sont dus à des classes de même fréquence).

Licence 2-S4 SI-MASS
Année 2018Cours de Statistiques inférentiellesPierre DUSART
2Chapitre1Lois statistiques
1.1 Introduction
Nous allons voir que si une variable aléatoire suit une certaine loi, alors ses réalisations (sous forme
d"échantillons) sont encadrées avec des probabilités de réalisation. Par exemple, lorsque l"on a une énorme
urne avec une proportionpde boules blanches alors le nombre de boules blanches tirées sur un échan-
tillon de taillenest parfaitement défini. En pratique, la fréquence observée varie autour depavec des
probabilités fortes autour depet plus faibles lorsqu"on s"éloigne dep.Nous allons chercher à faire l"inverse : l"inférence statistique consiste à induire les caractéristiques in-
connues d"une population à partir d"un échantillon issu de cette population. Les caractéristiques de
l"échantillon, une fois connues, reflètent avec une certaine marge d"erreur possible celles de la population.
1.1.1 Fonction de répartition
La densité de probabilitép(x)ou la fonction de répartitionF(x)définissent la loi de probabilité d"une
variable aléatoire continueX. Elles donnent lieu aux représentations graphiques suivantes :Figure1.1 - fonction répartition
La fonction de distribution cumuléeF(x)exprime la probabilité queXn"excède pas la valeurx:F(x) =P(Xx):
De même, la probabilité que X soit entreaetb(b > a) vautP(a < X < b) =F(b)F(a):
4CHAPITRE 1. LOIS STATISTIQUES1.1.2 Grandeurs observées sur les échantillons
L"espéranceE(X)d"une variable aléatoire discrèteXest donnée par la formuleE(X) =X
ix iP(xi): L"espérance est également appelée moyenne et notée dans ce casX. Sa variance2Xest l"espérance des carrés des écarts avec la moyenne :2X=E[(XX)2] =X
i(xiX)2P(xi) =X ix2iP(xi)2X:
Son écart-typeXest la racine positive de la variance.1.2 Lois usuelles
1.2.1 Loi normale ou loi de Gauss
Une variable aléatoire réelleXsuit une loi normale (ou loi gaussienne, loi de Laplace-Gauss) d"espérance
et d"écart type(nombre strictement positif, car il s"agit de la racine carrée de la variance2) si cette
variable aléatoire réelleXadmet pour densité de probabilité la fonctionp(x)définie, pour tout nombre
réelx, par : p(x) =1 p2e12 (x )2: Une telle variable aléatoire est alors dite variable gaussienne.Une loi normale sera notée de la manière suivanteN(;)car elle dépend de deux paramètres(la
moyenne) et(l"écart-type). Ainsi si une variable aléatoireXsuitN(;)alorsE(X) =etV(X) =2:
Lorsque la moyennevaut 0, et l"écart-type vaut 1, la loi sera notéeN(0;1)et sera appelée loi normale
standard. Sa fonction caractéristique vautet2=2. Seule la loiN(0;1)est tabulée car les autres lois (c"est-
à-dire avec d"autres paramètres) se déduise de celle-ci à l"aide du théorème suivant : SiYsuitN(;)
alorsZ=Y suitN(0;1). On notela fonction de répartition de la loi normale centrée réduite : (x) =P(Z < x) avecZune variable aléatoire suivantN(0;1).Propriétés et Exemples :(x) = 1(x),
(0) = 0:5;(1:645)0:95;(1:960)0:9750Pourjxj<2, une approximation depeut être utilisée; il s"agit de son développement de Taylor à
l"ordre 5 au voisinage de 0 : (x)0:5 +1p2 xx36 +x540Inversement, à partir d"une probabilité, on peut chercher la borne pour laquelle cette probabilité est
effective. Cours Proba-Stat / Pierre DUSART5Notation : on noteraz=2le nombre pour lequelP(Z > z=2) ==2
lorsque la variable aléatoire suit la loi normale standard.risque0:010:020:050:10valeur critiquez=22:582:331:961:645coefficient de sécuritéc99%98%95%90%
A l"aide des propriétés de la loi normale standard, on remarque que le nombrez=2vérifie également
P(Z < z=2) =
P(Z P(z=2< Z < z=2) =
P(jZj> z=2) =
La somme de deux variables gaussiennes indépendantes est elle-même une variable gaussienne (stabilité) :
SoientXetYdeux variables aléatoires indépendantes suivant respectivement les loisN(1;1)et N(2;2). Alors, la variable aléatoireX+Ysuit la loi normaleN(1+2;p 21+22).
1.2.2 Loi du2(khi-deux)
Définition 1SoitZ1;Z2;:::;Zune suite de variables aléatoires indépendantes de même loiN(0;1).
Alors la variable aléatoireP
i=1Z2isuit une loi appeléeloi du Khi-deuxàdegrés de liberté, notée 2(). Proposition 1.2.11. Sa fonction caractéristique est(12it)=2. 2. La densité de la loi du2()est
f (x) = 12 =2(=2)x=21ex=2pourx >0 0sinon.
oùest la fonction Gamma d"Euler définie par(r) =R1 0xr1exdx.
3. L"espérance de la loi du2()est égale au nombrede degrés de liberté et sa variance est2.
4. La somme de deux variables aléatoires indépendantes suivant respectivement2(1)et2(2)suit
aussi une loi du2avec1+2degrés de liberté. PreuveCalculons la fonction caractéristique deZ2lorsqueZsuitN(0;1). '(t) =E(eitZ2) =Z 1 1 eitz21p2ez2=2dz 1p2Z 1 1 e12 (12it)z2dz 1p2Z 1 1e 12 u2(12it)1=2dten posantu= (12it)1=2z '(t) = (12it)1=2 Maintenant pour la somme devariablesZ2iindépendantes, on a '(t) = (12it)=2: 6CHAPITRE 1. LOIS STATISTIQUESMontrons maintenant que la fonction de densité est correcte. Pour cela, calculons la fonction caractéris-
tique à partir de la densité : '(t) =E(eitx) =Z +1 0 eitx12 =2(=2)x=21ex=2dx 12 =2(=2)Z +1 0 x(1=2it)xdx 12 =2(=2)1(1=2it)(1=2it)=21Z +1 0 u=21euduen posantu= (1=2it)x 12 =2(=2)1(1=2it)=2Z +1 0 u=21eudu |{z} =(=2) '(t) =1(12it)=2 Calculons maintenant l"espérance et la variance. Selon la définition de la loi du2, chaque variable
Z isuit la loi normale centrée réduite. AinsiE(Z2i) =V ar(Zi) = 1etE(P i=1Z2i) =. De même, V(Zir) =E(Z4i)(E(Z2i))2=41:On sait que pour une loi normale centrée réduite4= 3donc V ar(Z2i) = 2etV ar(P
i=1Z2i) = 2: La dernière proposition est évidente de par la définition de la loi du2. Fonction inverse: on peut trouver une tabulation de la fonction réciproque de la fonction de répartition
de cette loi dans une table (en annexe) ou sur un logiciel tableur : 7!2;(FonctionKHIDEUX.inverse(;));
c"est-à-dire la valeur de2;telle queP(2()> 2;) =. Exemple : Pour= 0:990et= 5,2= 0:554 =20:99;5.Figure1.2 - fonction2inverse 1.2.3 Loi de Student
Définition 2SoientZetQdeux variables aléatoires indépendantes telles queZsuitN(0;1)etQsuit 2(). Alors la variable aléatoire
T=ZpQ=
suit une loi appeléeloi de Studentàdegrés de liberté, notéeSt(). Cours Proba-Stat / Pierre DUSART7Proposition 1.2.21. La densité de la loi de la loi de Student àdegrés de liberté est
f(x) =1p +12 )(=2)1(1 +x2=)+12 2. L"espérance n"est pas définie pour= 1et vaut 0 si2. Sa variance n"existe pas pour2et
vaut=(2)pour3. 3. La loi de Student converge en loi vers la loi normale centrée réduite.
Remarque : pour= 1, la loi de Student s"appelle loi de Cauchy, ou loi de Lorentz. 1.2.4 Loi de Fisher-Snedecor
Définition 3SoientQ1etQ2deux variables aléatoires indépendantes telles queQ1suit2(1)etQ2 suit2(2)alors la variable aléatoire F=Q1=1Q
2=2 suit une loi de Fisher-Snedecor à(1;2)degrés de liberté, notéeF(1;2). Proposition 1.2.3La densité de la loiF(1;2)est
f(x) =(1+22 )(1=2)(2=2) 1 2 1=2x1=21(1 +
1 2x) 1+22 six >0 (0sinon): Son espérance n"existe que si23et vaut2
22. Sa variance n"existe que si25et vaut22
2(1+22)
1(22)2(24).
Proposition 1.2.41. SiFsuit une loi de FisherF(1;2)alors1F suit une loi de FisherF(2;1). 2. SiTsuit une loi de Student àdegrés de liberté alorsT2suit une loi de FisherF(1;).
1.2.5 Fonctions inverses et TableurLoiNotationVariableFct RépartitionV. critiqueFonction inverse
GaussN(0;1)Zloi.normale.standard(z)z
loi.normale.standard.inverse(1)Khi-Deux 2()K 2khideux(k;;1)
;1;2inverse.Loi.f(;1;2)) 8CHAPITRE 1. LOIS STATISTIQUES
Chapitre2Convergences
2.1 Convergence en probabilité
2.1.1 Inégalités utiles
Inégalité de Markov simplifiée
SoitYune v.a.r.,gune fonction croissante et positive ou nulle sur l"ensemble des réels, vérifiantg(a)>0,
alors 8a >0;P(Ya)E(g(Y))g(a):
Preuve
E(g(Y)) =Z
g(y)f(y)dy=Z Y
[PDF] courbe de henry excel
[PDF] droite de henry pdf
[PDF] programmation linéaire exercices corrigés pdf
[PDF] programmation linéaire exercices corrigés
[PDF] programmation linéaire simplexe
[PDF] recherche opérationnelle programmation linéaire exercices corrigés pdf
[PDF] exercices recherche operationnelle
[PDF] theme astral chinois complet gratuit interpretation
[PDF] cours recherche opérationnelle methode de simplexe
[PDF] recherche opérationnelle simplexe exercices corrigés
[PDF] livre recherche opérationnelle pdf
[PDF] cours et exercices corrigés de recherche opérationnelle+pdf
[PDF] inpes
[PDF] methode boscher pdf download
[PDF] méthode boscher cahier de lecture pdf
P(z=2< Z < z=2) =
P(jZj> z=2) =
La somme de deux variables gaussiennes indépendantes est elle-même une variable gaussienne (stabilité) :
SoientXetYdeux variables aléatoires indépendantes suivant respectivement les loisN(1;1)et N(2;2). Alors, la variable aléatoireX+Ysuit la loi normaleN(1+2;p21+22).
1.2.2 Loi du2(khi-deux)
Définition 1SoitZ1;Z2;:::;Zune suite de variables aléatoires indépendantes de même loiN(0;1).
Alors la variable aléatoireP
i=1Z2isuit une loi appeléeloi du Khi-deuxàdegrés de liberté, notée 2(). Proposition 1.2.11. Sa fonction caractéristique est(12it)=2.2. La densité de la loi du2()est
f (x) = 12 =2(=2)x=21ex=2pourx >00sinon.
oùest la fonction Gamma d"Euler définie par(r) =R10xr1exdx.
3. L"espérance de la loi du2()est égale au nombrede degrés de liberté et sa variance est2.
4. La somme de deux variables aléatoires indépendantes suivant respectivement2(1)et2(2)suit
aussi une loi du2avec1+2degrés de liberté. PreuveCalculons la fonction caractéristique deZ2lorsqueZsuitN(0;1). '(t) =E(eitZ2) =Z 1 1 eitz21p2ez2=2dz 1p2Z 1 1 e12 (12it)z2dz 1p2Z 1 1e 12 u2(12it)1=2dten posantu= (12it)1=2z '(t) = (12it)1=2 Maintenant pour la somme devariablesZ2iindépendantes, on a '(t) = (12it)=2:6CHAPITRE 1. LOIS STATISTIQUESMontrons maintenant que la fonction de densité est correcte. Pour cela, calculons la fonction caractéris-
tique à partir de la densité : '(t) =E(eitx) =Z +1 0 eitx12 =2(=2)x=21ex=2dx 12 =2(=2)Z +1 0 x(1=2it)xdx 12 =2(=2)1(1=2it)(1=2it)=21Z +1 0 u=21euduen posantu= (1=2it)x 12 =2(=2)1(1=2it)=2Z +1 0 u=21eudu |{z} =(=2) '(t) =1(12it)=2Calculons maintenant l"espérance et la variance. Selon la définition de la loi du2, chaque variable
Z isuit la loi normale centrée réduite. AinsiE(Z2i) =V ar(Zi) = 1etE(P i=1Z2i) =. De même, V(Zir) =E(Z4i)(E(Z2i))2=41:On sait que pour une loi normale centrée réduite4= 3doncV ar(Z2i) = 2etV ar(P
i=1Z2i) = 2: La dernière proposition est évidente de par la définition de la loi du2.Fonction inverse: on peut trouver une tabulation de la fonction réciproque de la fonction de répartition
de cette loi dans une table (en annexe) ou sur un logiciel tableur :7!2;(FonctionKHIDEUX.inverse(;));
c"est-à-dire la valeur de2;telle queP(2()> 2;) =. Exemple : Pour= 0:990et= 5,2= 0:554 =20:99;5.Figure1.2 - fonction2inverse1.2.3 Loi de Student
Définition 2SoientZetQdeux variables aléatoires indépendantes telles queZsuitN(0;1)etQsuit2(). Alors la variable aléatoire
T=ZpQ=
suit une loi appeléeloi de Studentàdegrés de liberté, notéeSt().Cours Proba-Stat / Pierre DUSART7Proposition 1.2.21. La densité de la loi de la loi de Student àdegrés de liberté est
f(x) =1p +12 )(=2)1(1 +x2=)+122. L"espérance n"est pas définie pour= 1et vaut 0 si2. Sa variance n"existe pas pour2et
vaut=(2)pour3.3. La loi de Student converge en loi vers la loi normale centrée réduite.
Remarque : pour= 1, la loi de Student s"appelle loi de Cauchy, ou loi de Lorentz.1.2.4 Loi de Fisher-Snedecor
Définition 3SoientQ1etQ2deux variables aléatoires indépendantes telles queQ1suit2(1)etQ2 suit2(2)alors la variable aléatoireF=Q1=1Q
2=2 suit une loi de Fisher-Snedecor à(1;2)degrés de liberté, notéeF(1;2).Proposition 1.2.3La densité de la loiF(1;2)est
f(x) =(1+22 )(1=2)(2=2) 1 21=2x1=21(1 +
1 2x) 1+22 six >0 (0sinon):Son espérance n"existe que si23et vaut2
22. Sa variance n"existe que si25et vaut22
2(1+22)
1(22)2(24).
Proposition 1.2.41. SiFsuit une loi de FisherF(1;2)alors1F suit une loi de FisherF(2;1).2. SiTsuit une loi de Student àdegrés de liberté alorsT2suit une loi de FisherF(1;).
1.2.5 Fonctions inverses et TableurLoiNotationVariableFct RépartitionV. critiqueFonction inverse
GaussN(0;1)Zloi.normale.standard(z)z
loi.normale.standard.inverse(1)Khi-Deux 2()K2khideux(k;;1)
;1;2inverse.Loi.f(;1;2))8CHAPITRE 1. LOIS STATISTIQUES
Chapitre2Convergences
2.1 Convergence en probabilité
2.1.1 Inégalités utiles
Inégalité de Markov simplifiée
SoitYune v.a.r.,gune fonction croissante et positive ou nulle sur l"ensemble des réels, vérifiantg(a)>0,
alors8a >0;P(Ya)E(g(Y))g(a):
Preuve
E(g(Y)) =Z
g(y)f(y)dy=Z Y[PDF] droite de henry pdf
[PDF] programmation linéaire exercices corrigés pdf
[PDF] programmation linéaire exercices corrigés
[PDF] programmation linéaire simplexe
[PDF] recherche opérationnelle programmation linéaire exercices corrigés pdf
[PDF] exercices recherche operationnelle
[PDF] theme astral chinois complet gratuit interpretation
[PDF] cours recherche opérationnelle methode de simplexe
[PDF] recherche opérationnelle simplexe exercices corrigés
[PDF] livre recherche opérationnelle pdf
[PDF] cours et exercices corrigés de recherche opérationnelle+pdf
[PDF] inpes
[PDF] methode boscher pdf download
[PDF] méthode boscher cahier de lecture pdf
