[PDF] LIMITES DUNE FONCTION Théorème (Unicité de

View - Download LIMITES DUNE FONCTION

Previous PDF

Next PDF

Christophe Bertault — Mathématiques en MPSI

LIMITES D"UNE FONCTION

Les fonctions qu"on étudie en analyse sont généralement définies sur des intervalles ou des réunions d"intervalles comme

?ou[0,1[?[2,3], voire

2,π2

+π?. Dans ce chapitre, les lettresD,E... qui nous serviront d"ensembles de définition désigneront cependant des parties quelconques de?.

1 DÉFINITIONS DE LA LIMITE D"UNE FONCTION

1.1 LIMITE D"UNE FONCTION EN UN POINT

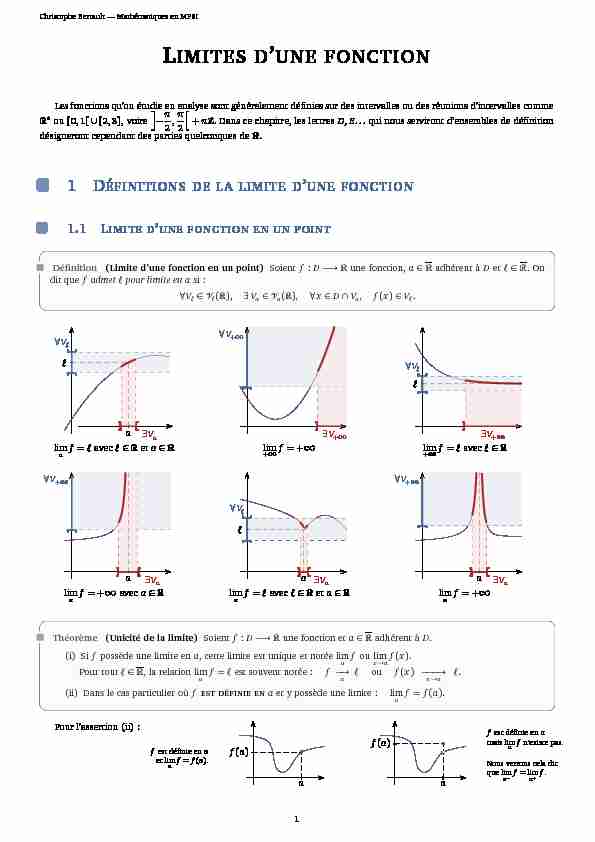
Définition(Limite d"une fonction en un point)Soientf:D-→?une fonction,a??adhérent àDet???. On

dit quef admet?pour limite en asi : ?V?? ??(?),?Va? ?a(?),?x?D∩Va,f(x)?V?. a ?Va ?V? limaf=?avec???eta?? ?V+∞ ?V+∞ lim+∞f= +∞ ?V+∞ ?V? lim+∞f=?avec??? a?Va ?V+∞ limaf= +∞aveca?? a ?Va ?V? limaf=?avec???eta?? a?Va ?V+∞ limaf= +∞ Théorème(Unicité de la limite)Soientf:D-→?une fonction eta??adhérent àD. (i) Sifpossède une limite ena, cette limite est unique et notée limafou limx→af(x).

Pour tout??

?, la relation limaf=?est souvent notée :f-→a?ouf(x)---→x→a?. (ii) Dans le cas particulier oùfEST DÉFINIE ENaet y possède une limite : limaf=f(a).

Pour l"assertion (ii) :

a f(a) ?fest définie ena et limaf=f(a). a f(a) fest définie ena mais limafn"existe pas.

Nous verrons cela dit

que lim a-f=lim a+f. 1

Christophe Bertault — Mathématiques en MPSI

Démonstration

(i) Par l"absurde, faisons l"hypothèse quefpossède deux limites?et??DISTINCTES. Il existe alors un voisinage

V ?de?et un voisinageV??de??DISJOINTS. Or par hypothèse surf, il existe deux voisinagesVaetV? adea pour lesquels :?x?D∩Va,f(x)?V?et :?x?D∩V? a,f(x)?V??.

Pourtant,aestadhérent àDetVa∩V?

aestun voisinage dea,doncD∩Va∩V? a?=∅,et pourtoutx?D∩Va∩V? a: f(x)?V?∩V??=∅— contradiction!

(ii) Faisons l"hypothèse quefest définie enaet possède une limite?ena. Pour tout voisinageV?de?, il existe

alors un voisinageVadeapour lequelf(x)?V?pour toutx?D∩Va. En particulier,fétant définie ena,

ceci indiquef(a)appartient àTOUTvoisinage de?.

Il en découle que???carf(a),+∞et-∞,f(a)sont des voisinages de+∞et-∞respectivement

ne contenant pasf(a). Finalement, pour tout? >0 :f(a)?]?-?,?+?[, donc?=f(a). Si vous n"êtes pas convaincus, supposez??=f(a)et choisissez?=1 2?? f(a)-???>0. Définition(Les 9 limites)Soientf:D-→?une fonction,a??adhérent àDet???.

•Cas où???eta??:

lim af=??? ?? >0,?α >0,?x?D,|x-a|< α=???f(x)-???< ?.

•Cas où?= +∞eta= +∞:

lim +∞f= +∞ ?? ?A>0,?B>0,?x?D,x>B=?f(x)>A.

•Cas où?=-∞eta= +∞:

lim +∞f=-∞ ?? ?A<0,?B>0,?x?D,x>B=?f(x)•Cas où?= +∞eta=-∞: lim -∞f= +∞ ?? ?A>0,?B<0,?x?D,xA.

•Cas où?=-∞eta=-∞:

lim -∞f=-∞ ?? ?A<0,?B<0,?x?D,x•Cas où???eta= +∞: lim +∞f=??? ?? >0,?B>0,?x?D,x>B=???f(x)-???< ?.

•Cas où???eta=-∞:

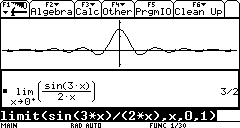
lim -∞f=??? ?? >0,?B<0,?x?D,x•Cas où?= +∞eta??\D: lim af= +∞ ?? ?A>0,?α >0,?x?D,|x-a|< α=?f(x)>A.

•Cas où?=-∞eta??\D:

lim af=-∞ ?? ?A<0,?α >0,?x?D,|x-a|< α=?f(x)J"utiliserai généralement des inégalités strictes, mais vous avez le droit de préférer les inégalités larges.

Exemplelimx→1x+2?x-1= +∞.

DémonstrationMontrons que :?A>0,?α >0,?x?]1,+∞[,|x-1|< α=?x+2?x-1>A.

SoitA>0. Pour toutx?]1,+∞[, minorons :x+2

?x-1?3?x-1?1?x-1.

On minore enSIMPLIFIANTet en vérifiant

que ce par quoi on minoreTEND TOU- JOURS VERS+∞quandxtend vers 1.On arrête de minorer quand onse sent capable de trouverα.

Or :1?x-1>A???x-1<1A?? |x-1|<1A2. Posonsα=1A2.

D"après ce qui précède :?x?]1,+∞[,|x-1|< α=?1 ?x-1>A. 2

Christophe Bertault — Mathématiques en MPSI

Exemplelimx→+∞x

2x2+1=1.

DémonstrationMontrons que :?? >0,?B>0,?x??,x>B=????x2x2+1-1???

Soit? >0. Pour toutx??, majorons :???x2

x2+1-1??? =1x2+1?1x2.

On majore enSIMPLIFIANTet en vérifiant

que ce par quoi on majoreTEND TOU- JOURS VERS0 quandxtend vers+∞.On arrête de majorer quand onse sent capable de trouverB.

Or pour toutx>0 :1x2< ???x>1??. PosonsB=1??.

D"après ce qui précède :?x??,x>B=????x2

x2+1-1???

Exemplelimx→+∞x2-x= +∞.

DémonstrationMontrons que :?A>0,?B>0,?x??,x>B=?x2-x>A.

SoitA>0. Pour toutx?2 :x-1?1, doncx2-x=x(x-1)?x.

On minore enSIMPLIFIANTet en vérifiant

que ce par quoi on minoreTEND TOU- JOURS VERS+∞quandxtend vers+∞.On arrête de minorer quand onse sent capable de trouverB. PosonsB=max2,A. D"après ce qui précède :?x??,x>B=?x2-x>A.

Théorème(Limite finie et caractère localement borné)Soientf:D-→?eta??adhérent àD.

Sifpossède une limiteFINIEena,fest bornée au voisinage dea.

DémonstrationPar hypothèse, il existe un voisinageVadeasur lequel??f(x)-???<1. Il en découle quefest

bornée surD∩Vacar pour toutx?D∩Va:??f(x)??=??f(x)-?+??????f(x)-???+|?|?|?|+1.

1.2 LIMITE À GAUCHE/À DROITE D"UNE FONCTION EN UN POINT

Définition-théorème(Limite à gauche/à droite d"une fonction)Soientf:D-→?une fonction eta??.

•Limite à gauche :Siaest adhérent àD∩]-∞,a[, on dit quef possède une limite à gauche en asif

D∩]-∞,a[

possède une limite ena. Cette limite est notée lima-f, limx→a-f(x)ou encore limx→ax

Pour tout??

?, dire que?=lima-f??revient donc à dire que : ??? >0,?α >0,?x?D,a-α 0,?α >0,?x?D,a-α Asi?= +∞ ?A<0,?α >0,?x?D,a-α •Limite à droite :On définit de même la notion delimite à droiteà partir de la fonction restreintef

D∩]a,+∞[sia

est adhérent àD∩]a,+∞[. En termes de quantificateurs, remplacez simplementa-α

Les limites à gauche/à droite ne sont jamais que des limites au sens initial du chapitre mais appliquées à des restrictions.

Cela justifie leur unicité et la possibilité que nous avons deleur accorder une notation.

Exemplelimx→0+1x= +∞.

DémonstrationSoitA>0. Nous cherchons un réelα >0 pour lequel pour toutx?]0,α[:1x>A.

Or pout toutx>0 :1

x>A??x<1A. Nous pouvons donc choisirα=1A. 3

Christophe Bertault — Mathématiques en MPSI

On montre de même que lim

x→0-1 x=-∞. En revanche, d"après le théorème qui suit, la limite limx→01xN"EXISTE PAS!

Théorème(Caractérisation de la limite à l"aide des limites à gauche/à droite)Soientf:D-→?une fonction,

?eta??adhérent àD∩]-∞,a[et àD∩]a,+∞[. (i) Sifest définie ena: limaf=???lima-f=lima+f=?

ET?=f(a).

(ii) SifN"estPASdéfinie ena: limaf=???lima-f=lima+f=?.

Pour bien comprendre la condition " et?=f(a)» de l"assertion (i), jetez un oeil aux deux figures de la fin de lapage 1.

DémonstrationMontrons seulement (i).

•Si limaf=?, nous savons déjà que?=f(a). On obtient ensuite les égalités lima-f=lima+f=?par simple

restriction du domaine àD∩]-∞,a[etD∩]a,+∞[dans la définition de la limite limaf=?.

•Réciproquement, faisons l"hypothèse que lima-f=lima+f=?=f(a). En particulier???et nous voulons

montrer que lim af=?. Soit? >0. Il existe des réelsα->0 etα+>0 pour lesquels pour toutx?D: a-α-ExempleSi on notefla fonctionx?-→"exsix?0

1-xsix<0de?dans?, alors limx→0f(x) =1.

DémonstrationTrois raisons : limx→0-(1-x) =1, limx→0+ex=1 etf(0) =1.

2 MANIPULATION DES LIMITES

2.1 OPÉRATIONS SUR LES LIMITES

Il se passe avec les fonctions la même chose qu"avec les suites pour les opérations de somme, produit, multiplication par

un scalaire et inverse — en particulier, mêmes formes indéterminées. Refaites un tour du côté des suites!

Théorème(Composition de limites)Soientf:D-→Eetg:E-→?deux fonctions,a??adhérent àD,b??

adhérent àEetc? ?. Si limaf=bet limbg=c, alors limag◦f=c.

DémonstrationSoitVcun voisinage dec.

Comme lim

bg=c, il existe un voisinageVbdebpour lequelg(x)?Vcpour toutx?E∩Vb, et comme limaf=b, il existe un voisinageVadeapour lequelf(x)?Vbpour toutx?D∩Va. Par composition :?x?D∩Va,g◦f(x)?Vc, donc en effet limag◦f=c. Va D

3... et donc aussi un voisinageVadea

quefenvoie dansVb. VbE

2... il existe un voisinageVbdeb

quegenvoie dansVc... Vc

1Pour tout voisinageVcdec...

4Finalementg◦fenvoieVadansVcd"un coup d"un seul.

fg g◦f a? b c 4

Christophe Bertault — Mathématiques en MPSI

DémonstrationSimple composition des trois limites : limx→+∞e-x=0, limy→0y

2+1(y+1)2=1 et limz→1lnz=0.

?Attention !Si limx→+∞f(x) =???, on ne peut pas affirmerSANS PREUVEque : limx→+∞xx+f(x)=limx→+∞xx+?et

lim

x→+∞f(x)x=limx→+∞?x. Lapremière égalitéestvraie, maiscommentlejustifiersans calculerexplicitement limx→+∞x

x+f(x)?

Quant à la deuxième, elle est fausse si?=1 — forme indéterminée 1+∞. En résumé :

Quand on passe à la limite, onNEpeutJAMAISle faire " par morceaux » en remplaçant tel morceau par sa limite et en laissant le reste intact.

2.2 PASSAGE À LA LIMITE DANS UNE INÉGALITÉ ET OPÉRATION INVERSE

Théorème(Limites et inégalités strictes)Soienta??adhérent àD,f:D-→?une fonction possédant une limite

?enaetm,M??. (i) Si? m, alorsf(x)>mau voisinage dea.

DémonstrationProuvons (ii). Si?= +∞, il existe un voisinageVadeasur lequelf(x)?]m,+∞[. Si???,

quotesdbs_dbs33.pdfusesText_39

[PDF] caractérisation séquentielle de la limite

[PDF] demonstration de l'unicité de la limite d'une fonction

[PDF] théorème de la limite monotone

[PDF] montrer que f est minorée et atteint sa borne inférieure

[PDF] démonstration variance probabilité

[PDF] relation de chasles parallélogramme

[PDF] vecteurs opposés

[PDF] vecteur nul exemple

[PDF] remplacement alternateur espace 3 2.2 dci

[PDF] tuto changement alternateur espace 4

[PDF] demontage alternateur espace 4 2.2 dci

[PDF] demontage alternateur espace 2 diesel

[PDF] demontage alternateur espace 4 1.9 dci

[PDF] prix changement alternateur espace 3

[PDF] changer alternateur renault espace 3