[PDF] Cours de mathématiques - Exo7

View - Download Cours de mathématiques - Exo7

Previous PDF

Next PDF

Dérivée d"une fonctionExo7

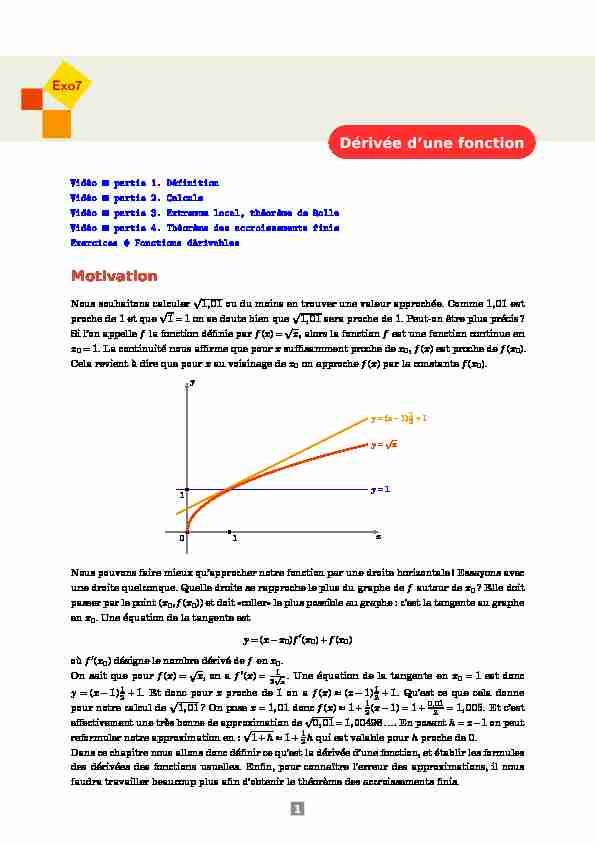
MotivationNous souhaitons calculerp1,01ou du moins en trouver une valeur approchée. Comme 1,01 est

proche de 1 et quep1AE1 on se doute bien quep1,01sera proche de 1. Peut-on être plus précis? Si l"on appellefla fonction définie parf(x)AEpx, alors la fonctionfest une fonction continue en x0AE1. La continuité nous affirme que pourxsuffisamment proche dex0,f(x) est proche def(x0). Cela revient à dire que pourxau voisinage dex0on approchef(x) par la constantef(x0).xy 1

01yAE1yAEpxyAE(x¡1)12

Å1Nous pouvons faire mieux qu"approcher notre fonction par une droite horizontale! Essayons avec une droite quelconque. Quelle droite se rapproche le plus du graphe defautour dex0? Elle doit

passer par le point (x0,f(x0)) et doit "coller» le plus possible au graphe : c"est la tangente au graphe

enx0. Une équation de la tangente est yAE(x¡x0)f0(x0)Åf(x0) oùf0(x0) désigne le nombre dérivé defenx0.

On sait que pourf(x)AEpx, on af0(x)AE12

px. Une équation de la tangente enx0AE1 est donc yAE(x¡1)12 Å1. Et donc pourxproche de 1 on af(x)¼(x¡1)12

Å1. Qu"est ce que cela donne

pour notre calcul dep1,01? On posexAE1,01 doncf(x)¼1Å12(x¡1)AE1Å0,012

AE1,005. Et c"est

effectivement une très bonne de approximation dep0,01AE1,00498.... En posanthAEx¡1 on peut reformuler notre approximation en :p1Åh¼1Å12 hqui est valable pourhproche de 0.

Dans ce chapitre nous allons donc définir ce qu"est la dérivée d"une fonction, et établir les formules

des dérivées des fonctions usuelles. Enfin, pour connaître l"erreur des approximations, il nous

faudra travailler beaucoup plus afin d"obtenir le théorème des accroissements finis.1 2 1.

Dérivée

1.1.

Dérivée en un point

SoitIun intervalle ouvert deRetf:I!Rune fonction. Soitx02I.Définition 1 festdérivable enx0si letaux d"accroissementf(x)¡f(x0)x¡x0a une limite finie lorsquextend versx0. La limite s"appelle alors lenombre dérivédefenx0et est notéf0(x0). Ainsi f

0(x0)AElimx!x0f(x)¡f(x0)x¡x0Définition 2

f estdérivable surIsifest dérivable en tout pointx02I. La fonctionx7!f0(x) est la fonction dérivéedef, elle se notef0oudfdx .Exemple 1 La fonction définie parf(x)AEx2est dérivable en tout pointx02R. En effet : On a même montré que le nombre dérivé defenx0est 2x0, autrement dit :f0(x)AE2x.Exemple 2 Montrons que la dérivée def(x)AEsinxestf0(x)AEcosx. Nous allons utiliser les deux assertions suivantes :sinxx

¡¡¡!x!01 et sinp¡sinqAE2sinp¡q2

¢cospÅq2

Remarquons déjà que la première assertion prouvef(x)¡f(0)x¡0AEsinxx !1 et doncfest dérivable enx0AE0 etf0(0)AE1.

Pourx0quelconque on écrit :

x¡x02

¢cosxÅx02

Lorsquex!x0alors d"une partcosxÅx02

!cosx0et d"autre part en posantuAEx¡x02alorsu!0 et on asinuu !1. Ainsif(x)¡f(x0)x¡x0!cosx0et doncf0(x)AEcosx.1.2.T angente

La droite qui passe parles points distincts (x0,f(x0)) et (x,f(x)) a pourcoefficient directeurf(x)¡f(x0)x¡x0.

À la limite on trouve que le coefficient directeur de la tangente estf0(x0). Une équation de la

tangenteau point (x0,f(x0)) est donc : yAE(x¡x0)f0(x0)Åf(x0) 3 M 0x 0xM 1.3.

Autres écritures de la dérivée

Voici deux autres formulations de la dérivabilité defenx0.Proposition 1 -fest dérivable enx0si et seulement si limh!0f(x0Åh)¡f(x0)h existe et est finie. -fest dérivable enx0si et seulement s"il existe`2R(qui seraf0(x0)) et une fonction ":I!Rtelle que"(x)¡¡¡¡!x!x00 avec

Il s"agit juste de reformuler la définition def0(x0). Par exemple, après division parx¡x0, la deuxième

écriture devientf(x)¡f(x0)x¡x0AE`Å"(x).Proposition 2 SoitIun intervalle ouvert,x02Iet soitf:I!Rune fonction. -Sifest dérivable enx0alorsfest continue enx0. -Sifest dérivable surIalorsfest continue surI.Démonstration Supposonsfdérivable enx0et montrons qu"elle est aussi continue en ce point.

Voici une démonstration concise : partant de l"écriture alternative donnée dans la proposition

1 , nous

écrivons

f(x)AEf(x0)Å(x¡x0)`|{z} !0Å(x¡x0)"(x)|{z} !0. Doncf(x)!f(x0) lorsquex!x0et ainsifest continue enx0.

On reprend cette démonstration sans utiliser les limites mais uniquement la définition de continuité

et dérivabilité :

Fixons"0È0 et écrivonsf(x)AEf(x0)Å(x¡x0)`Å(x¡x0)"(x) grâce à la proposition1 , où"(x)¡¡¡¡!x!x00 et

4 `AEf0(x0). Choisissons±È0 de sorte qu"il vérifie tous les points suivants : -±É1 -±j`jÇ"0 -sijx¡x0jDZalorsj"(x)jÇ"0(c"est possible car"(x)!0)

Alors l"égalité ci-dessus devient :

ɱj`j ű"0pourjx¡x0jDZ

É"0Å"0AE2"0Nous venons de prouver que sijx¡x0j DZalors¯¯f(x)¡f(x0)¯¯Ç2"0, ce qui exprime exactement quef

est continue enx0.Remarque La réciproque estfausse: par exemple, la fonction valeur absolue est continue en 0 mais n"est pas dérivable en 0.xy 1

01yAEjxjEn effet, le taux d"accroissement def(x)AEjxjenx0AE0 vérifie :

f(x)¡f(0)x¡0AEjxjx AE8 :Å1 sixÈ0

¡1 sixÇ0.

Il y a bien une limite à droite (qui vautÅ1), une limite à gauche (qui vaut¡1) mais elles ne

sont pas égales : il n"y a pas de limite en 0. Ainsifn"est pas dérivable enxAE0. Cela se lit aussi sur le dessin il y a une demi-tangente à droite, une demi-tangente à gauche mais elles ont des directions différentes.Mini-exercices 1. Montrer que la fonct ionf(x)AEx3est dérivable en tout pointx02Ret quef0(x0)AE3x20. 2. Montrer que la fonctionf(x)AEpxest dérivable en tout pointx0È0 et quef0(x0)AE12 px 0.

3.Montrer que la fonctionf(x)AEpx(qui est continue enx0AE0) n"est pas dérivable en

x0AE0. 4. Calculer l"équation de la tangente (T0) à la courbe d"équationyAEx3¡x2¡xau point d"abscissex0AE2. Calculerx1afin que la tangente (T1) au point d"abscissex1soit paral- lèle à (T0). 5. Montrer que si une fonction fest paire et dérivable, alorsf0est une fonction impaire. 5 2.

Calcul des dérivées

2.1.

Somme, produit,... Proposition 3

Soientf,g:I!Rdeux fonctions dérivables surI. Alors pour toutx2I: -(fÅg)0(x)AEf0(x)Åg0(x), -(¸f)0(x)AE¸f0(x) où¸est un réel fixé, -(f£g)0(x)AEf0(x)g(x)Åf(x)g0(x), -³1f

0(x)AE¡f0(x)f(x)2(sif(x)6AE0),

-³fg Il est plus facile de mémoriser les égalités de fonctions : (fÅg)0AEf0Åg0,(¸f)0AE¸f0,(f£g)0AEf0gÅf g0,µ1f 0

AE¡f0f

2,µfg

0

AEf0g¡f g0g

2.Démonstration

Prouvons par exemple (f£g)0AEf0gÅf g0.

Fixonsx02I. Nous allons réécrire le taux d"accroissement def(x)£g(x) :

Ceci étant vrai pour toutx02Ila fonctionf£gest dérivable surIde dérivéef0gÅf g0.2.2.Dérivée de fonctions usuelles Le tableau de gauche est un résumé des principales formules à connaître,xest une variable. Le

tableau de droite est celui des compositions (voir paragraphe suivant),ureprésente une fonction x7!u(x).FonctionDérivée x nnx n¡1(n2Z)1 x¡ 1x 2px1 2 1px x

®®x®¡1(®2R)e

xe xlnx1 x cosx¡sinxsinxcosxtanx1Åtan2xAE1cos

2xFonctionDérivée

u nnu

0un¡1(n2Z)1

u¡ u0u 2pu1 2 u0pu u

®®u0u®¡1(®2R)e

uu

0eulnuu

0u cosu¡u0sinusinuu

0cosutanuu

0(1Åtan2u)AEu0cos

2u 6

Remarque

-Notez que les formules pourxn,1x pxetx®sont aussi des conséquences de la dérivée de l"exponentielle. Par exemplex®AEe®lnxet donc ddx (x®)AEddx (e®lnx)AE®1x e®lnxAE®1x x®AE®x®¡1. Si vous devez dériver une fonction avec un exposant dépendant dexil faut absolument repasser à la forme exponentielle. Par exemple sif(x)AE2xalors on réécrit d"abord f(x)AEexln2pour pouvoir calculerf0(x)AEln2¢exln2AEln2¢2x.2.3.Composition

Proposition 4

Sifest dérivable enxetgest dérivable enf(x) alorsg±fest dérivable enxde dérivée : La preuve est similaire à celle ci-dessus pour le produit en écrivant cette fois :

g±f(x)¡g±f(x0)x¡x0AEg¡f(x)¢¡g¡f(x0)¢f(x)¡f(x0)£f(x)¡f(x0)x¡x0¡¡¡¡!x!x0g0¡f(x0)¢£f0(x0).Exemple 3

Calculons la dérivée deln(1Åx2). Nous avonsg(x)AEln(x) avecg0(x)AE1x; etf(x)AE1Åx2avec f0(x)AE2x. Alors la dérivée de ln(1Åx2)AEg±f(x) est g±f¢0(x)AEg0¡f(x)¢¢f0(x)AEg0¡1Åx2¢¢2xAE2x1Åx2.Corollaire 1 SoitIun intervalle ouvert. Soitf:I!Jdérivable et bijective dont on notef¡1:J!Ila bijection réciproque. Sif0ne s"annule pas surIalorsf¡1est dérivable et on a pour tout x2J: f¡1¢0(x)AE1f

0¡f¡1(x)¢Démonstration

NotonsgAEf¡1la bijection réciproque def. Soity02Jetx02Itel quey0AEf(x0). Le taux d"accroisse- ment degeny0est : g(y)¡g(y0)y¡y0AEg(y)¡x0f

¡g(y)¢¡f(x0)

Lorsquey!y0alorsg(y)!g(y0)AEx0et donc ce taux d"accroissement tend vers1f

0(x0). Ainsig0(y0)AE

7 1 f

0(x0).Remarque

Il peut être plus simple de retrouver la formule à chaque fois en dérivant l"égalité f

¡g(x)¢AEx

oùgAEf¡1est la bijection réciproque def.En effet à droite la dérivée dexest 1; à gauche la dérivée def¡g(x)¢AEf±g(x) estf0¡g(x)¢¢g0(x).

L"égalitéf¡g(x)¢AExconduit donc à l"égalité des dérivées : f

0¡g(x)¢¢g0(x)AE1.

MaisgAEf¡1donc¡f¡1¢0(x)AE1f

0¡f¡1(x)¢.Exemple 4

Soitf:R!Rla fonction définie parf(x)AExÅexp(x). Étudionsfen détail.

Tout d"abord :

1.f est dérivable carfest la somme de deux fonctions dérivables. En particulierfest continue. 2.fquotesdbs_dbs33.pdfusesText_39

[PDF] exercice dérivabilité en un point

[PDF] exercices dérivabilité terminale

[PDF] fonction non dérivable

[PDF] exercices dérivabilité mpsi

[PDF] fonction dérivable en 0

[PDF] progression spiralée maths première s

[PDF] dérivées usuelles

[PDF] dérivé de

[PDF] exercices dérivées 1ere sti2d

[PDF] derivee 1sti2d

[PDF] on souhaite que le raccordement se fasse sans cassure en i

[PDF] raccordement de deux fonctions

[PDF] le profil d un toboggan est constitué de deux parties

[PDF] raccordement de courbes représentatives de fonctions

[PDF] raccordement routier maths