 Chapitre 1.6 – Loscillation vertical dun système bloc-ressort
Chapitre 1.6 – Loscillation vertical dun système bloc-ressort
L'application de la 2ième loi de Newton à un système masse-ressort oscillant à la verticale sans frottement sous l'effet de la gravité génère une équation.
 Résolution Énoncé
Résolution Énoncé
Bilan des forces exercées sur le système : – force exercée par le ressort sur la masse elle est propor- tionnelle à l'allongement du ressort
 Oscillateur harmonique Oscillateur harmonique
Oscillateur harmonique Oscillateur harmonique
13 nov. 2017 Exercice 2 : Une masse et deux ressorts ... Exercice 3 : Oscillateur masse-ressort vertical z. 0 z(t). O. M. 1 ⊳ Système : le cylindre de masse m ...
 1 Oscillateur harmonique
1 Oscillateur harmonique
8 sept. 2013 Une application importante concerne le système masse-ressort vertical. Exercices de niveau 2. Exercice 4. La force exercée par la charge ...
 Étude dun oscillateur (système masse-ressort)
Étude dun oscillateur (système masse-ressort)
18 juin 2012 linéaire du point B sur l'axe vertical. A l'équilibre ... Cours de mécanique (PDF) : Oscillation verticale du système masse-ressort et étude.
 Influence dun temps limite à lépuisement en course à pied sur la
Influence dun temps limite à lépuisement en course à pied sur la
déplacement vertical du centre de masse respectivement. Le compression de la jambe-ressort
 Phy 12a/12b Oscillateur harmonique : corrections 2013-2014
Phy 12a/12b Oscillateur harmonique : corrections 2013-2014
Système : le cube de masse constante m = ρc a3. Repère : R(Ok) avec Une masse m est accrochée à un ressort sans masse de raideur k et de longueur à vide l0.
 Chapitre 4 Les oscillateurs libres
Chapitre 4 Les oscillateurs libres
21 nov. 2003 Deuxième exemple : le système masse ressort vertical. Prenons le même ressort de raideur k et plaçons le verticalement. Il est accroché en ...
 Cours de mécanique - M13-Oscillateurs
Cours de mécanique - M13-Oscillateurs
3 Système solide-ressort vertical sans frottement. Problème 5. Soit un point M de masse m accroché à l'extrémité d'un ressort vertical sans masse. A t = 0 on
 Système masse-ressort Méthode 2 : Pendule
Système masse-ressort Méthode 2 : Pendule
Système masse-ressort au repos. On considère une masse m suspendue à un ressort vertical (raideur k longueur à vide l0). À l'équilibre
 Chapitre 1.6 – Loscillation vertical dun système bloc-ressort
Chapitre 1.6 – Loscillation vertical dun système bloc-ressort
L'application de la 2ième loi de Newton à un système masse-ressort oscillant à la verticale sans frottement sous l'effet de la gravité génère une équation.
 Cours de mécanique - M13-Oscillateurs
Cours de mécanique - M13-Oscillateurs
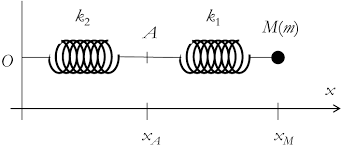
2 Système solide-ressort horizontal sans frottement. 2.1 Problème 4 Soit un point M de masse m accroché à l'extrémité d'un ressort vertical sans masse.
 Résolution Énoncé
Résolution Énoncé
Le ressort vertical sans masse posée sur lui a une longueur . Lorsqu'on pose la masse En établissant le bilan des forces agissant sur un système à.
 Oscillateur harmonique Oscillateur harmonique
Oscillateur harmonique Oscillateur harmonique
13 nov. 2017 Exercice 3 : Oscillateur masse-ressort vertical ... 2 - On considère le système ci-contre où ki et l0i sont les raideurs et longueurs à vide ...
 Physique 5 Comportement dynamique dun système au voisinage d
Physique 5 Comportement dynamique dun système au voisinage d
3.2 Système masse-ressort vertical . s'appliquer à un système masse-ressort ou bien à un circuit LC. Toutefois
 Étude dun oscillateur (système masse-ressort)
Étude dun oscillateur (système masse-ressort)
18 juin 2012 système masse-ressort se basant sur le TP et faisant apparaître les conditions initiales et les ... linéaire du point B sur l'axe vertical.
 LOSCILLATEUR HARMONIQUE
LOSCILLATEUR HARMONIQUE
I. Première observation : mouvement d'une masse accro- chée à un ressort. 1. En classe. Expérience : si on accroche une masse à un ressort vertical à spires
 Oscillateur harmonique
Oscillateur harmonique
Représenter un système masse-ressort horizontal : Exercice 5 : Bille accrochée à un ressort vertical ... Représenter le système masse-ressort aux.
 Système masse-ressort Une masse fixée à lextrémité libre dun
Système masse-ressort Une masse fixée à lextrémité libre dun
Une masse de 100 g oscille verticalement à l'extrémité libre d'un ressort. La position d'équilibre avec la masse suspendue correspond à un allongement de 2 cm
 COURS DE MECANIQUE - VIBRATIONS 1ère année
COURS DE MECANIQUE - VIBRATIONS 1ère année
Figure 6.6 : Système masse / ressort vertical a) ressort seul ni tendu ni comprimé b) système à l'équilibre
 Chapitre 16 – L’oscillation vertical d’un système bloc-ressort
Chapitre 16 – L’oscillation vertical d’un système bloc-ressort
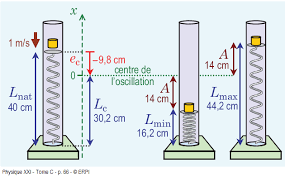
L’énergie d’un système masse-ressort à la verticale Analysons l’énergie d’un système masseressort oscillant à la verticale avec les équations du - mouvement suivantes selon la convention x =y =0 : x (t) = A sin (? t +?) et () = = A ? (? t +?) t x t v x t cos d d où ?= k / m ondition d’équilibreC : x = y =0
 Les oscillateurs harmoniques amortis et non amortis en mécanique
Les oscillateurs harmoniques amortis et non amortis en mécanique
ressorts ou plac ees a l’extr emit e des pendules) a des syst emes continus ou la masse est r epartie continumen^ t dans l’espace (par exemple le long d’une corde) Ce cours devrait donc vous permettre d’utiliser et d’approfondir les notions de m ecanique acquises en L1 et au 1er semestre de L3 a etablir un lien avec le cours
 LE SYSTEME MASSE RESSORT - Physagreg
LE SYSTEME MASSE RESSORT - Physagreg
LE SYSTEME MASSE RESSORT La force F exercée par le ressort sur le solide accroché au bout du ressort est appelée force de rappel Elle est proportionnelle à l’allongement x du ressort : F kxi & avec k la constante de raideur du ressort et s’exprime N m1 Détermination de k : On suspend le ressort verticalement
 Chapitre 14 : Système solide-ressort - Physagreg
Chapitre 14 : Système solide-ressort - Physagreg
Le système serait donc constitué d’un ressort de longueur à vide l 0 qui lorsque qu’on lui accroche une masse m s’étire jusqu’à la longueur l : b Celui que l’on utilise en théorie (1) : Le ressort est horizontal une masse (ponctuelle) est accrochée à son extrémité
Quelle est la différence entre un ressort horizontal et vertical ?
En effet, quand le ressort est horizontal, la position d’équilibre correspond à la longueur à vide (car pas de force appliquée au ressort). Mais en vertical, le ressort est soumis à une force qui tire la masse vers le bas (correspondant au poids de la masse) : la longueur du ressort à l’équilibre, notée l éq, ne sera donc pas égale à l 0.
Comment utiliser le système masse-ressort vertical ?
C’est ce que nous allons voir tout de suite avec le deuxième exemple : le système masse-ressort vertical. On prend le même ressort et la même masse que précédemment mais on attache cette fois-ci le ressort au plafond. L’axe est pris vers le bas afin que uext corresponde là encore à ux.
Comment trouver la même équation que le ressort horizontal ?
On retrouve la même équation que pour le ressort horizontal : c’est normal, on trouvera toujours cette équation si on prend l’origine du repère au niveau de la position d’équilibre, cela permet comme on vient de le voir « d’annuler » le second membre de l’équation différentielle.
Quels sont les différents types de systèmes de masse-ressort ?
Commençons donc par l’exemple le plus simple : le système masse-ressort horizontal. Le système masse-ressort horizontal est très simple : on considère un ressort de longueur à vide l 0 et de raideur k, accroché à un point fixe à son extrémité gauche, et à un objet de masse m à son extrémité droite (l’objet est parfois appelé masse) :
Oscillateurs lineaires
Cours et exercicesk
m kk m k mk kL3 Physique-Chimie { Universite Paris-Sud
jean-luc.raimbault@u-psud.fr { 2019-2020 2Chapter 1
Introduction
Notion d'oscillateur
Un systeme physique possede des positions d'equilibres stables lorsqu'il existe des forces au sein m^eme du systeme qui tendent a le ramener vers les positions d'equilibre. Sous l'eet d'une perturbation exterieure, une des reponses possibles du systeme est un mode d'oscillation (ou vibration) periodique, generalement amorti, qui le ramene progressivement vers sa position d'equilibre. L'archetype du systeme mecanique presentant un tel comportement est donne par le couple masse-ressort ou par les dierents types de pendules.k mx(t)m` (t)(t)` Figure 1.1: Exemples d'oscillateurs mecaniques : systeme masse-ressort, pendule simple et pendule de torsion. Un oscillateur est dit \harmonique" si sa position au cours du temps est une fonction sinusodale. L'amplitude de l'oscillateur peut decro^tre si le systeme est soumis a des frottements mais l'evolution peut rester periodique si les frottements ne sont pas trop importants. Il est facile de montrer dans ce cas, que l'acceleration et la force de rappel doivent ^etre proportionnelle et opposee, ce qui implique que la force de rappel soit proportionnelle au deplacement: x(t) =asin(!t+'))x(t)/ x(t))F/ x(t) 3 Pour cette raison, dans cette situation, on parle egalement d'\oscillateurs lineaires". On peut remarquer que si tous les oscillateurs ne sont pas lineaires (et donceventuellement anharmoniques) - et c'est m^eme le cas le plus frequent - il n'en reste pas moins vrai que tous les oscillateurs sont lineaires pour des ecarts a l'equilibre susamment faibles. En eet, une force de rappel lineaire est associee a une energie potentielle quadra- tique (a 1 dimensionF dEP=dx). Dans la situation la plus generaleEp(x) est une fonction quelconque de la positionxque l'on peut developper autour d'une position d'equilibre x: E p(x) =Ep(x) + (xx)dEp(x)dx +12 (xx)2d2Ep(x)dx 2+ Les positions d'equilibre etant determinees par la condition dEp(x)dx = 0, et le choix de l'origine des energies restant libre, on voit que le terme dominant pour les petits deplacements autour de l'equilibre est le terme quadratique, ce qui correspond au cas des oscillateurs lineaires1.(t)`
ur! u! T!P=m!gM(`,)!
gE p mg`mg`approximation harmoniqueFigure 1.2: Pendule simple et approximation harmonique de son energie potentielle de pesanteur. Du fait de ce caractere generique, on rencontre des oscillateurs lineaires dans tous les domaines de la physique. En plus des systemes mecaniques deja cites, il est facile d'en mettre en evidence dans le domaine de l'electricite ou de l'electronique (circuit LC ou RLC), de l'optique (susceptibilite lineaire des materiaux), de la physique des solides (oscillations plasma des metaux), de la mecanique quantique (niveaux1 Plus precisement, les positions d'equilibres stables exigeant que la derivee seconde de l'energiepotentielle soit positive, l'energie potentielle des oscillateurs harmoniques est une fonction quadra-
tiqueetpositive de la position. 4 d'energie d'une molecule di-atomique), ou de la mecanique des uides (oscillations de l'atmosphere dans certaines circonstances) ...V0cos! tLi(t)R
Cmm k Figure 1.3: Exemple d'un oscillateur electrique (circuit RLC) et d'un modele d'oscillateur quantique (molecule diatomique). Outre la force de rappel lineaire, un oscillateur peut ^etre soumis a des forces additionnelles, comme des forces de frictions dues au milieu ambiant et des forces exterieures appliquees a l'oscillateur. Ces 2 forces ont des eets opposes sur les oscil- lateurs : les forces de friction s'accompagnent de la perte d'energie de l'oscillateur, tandis que les forces exterieures peuvent ^etre a l'origine d'un apport d'energie au systeme. Du point de vue mathematique, un oscillateur lineaire dissipatif force a 1 degre de liberte, c'est-a-dire dont la description du mouvement ne requiert qu'une seule variable, est decrit par une equation dierentielle lineaire du second ordre, qui peut s'ecrire de la facon suivante dans un systeme d'unites adaptees : (t) =(t)1Q _(t) +f(t) ou(t) mesure l'ecart a la position d'equilibre a l'instantt,Qest un parametre mesurant le degre d'amortissement du milieu etf(t) une force exterieure appliquee a l'oscillateur.Contenu et plan du cours
Dans le 2eme chapitre de ce cours, nous commencerons par detailler le comporte- ment d'un seul oscillateur lineaire en regime libre, c'est a dire en absence de forces exterieures. Puis, nous etudierons le couplage de 2 oscillateurs lineaires de facon a etudier le comportement des systemes dits a 2 degres de liberte. Dans ce dernier cas, le systeme a etudier sera decrit par 2 equations dierentielles couplees :1(t) =1(t)1Q
1_1(t) +C(21);
2(t) =2(t)1Q
2_2(t)C(21);
5 ou le dernier terme des seconds membres est un terme de couplage entre les 2 os- cillateurs. Les mathematiques orent des methodes extr^emement puissantes pour resoudre ce type de systemes dierentiels lineaires generalisables a des systemes a un plus grand nombre de degres de liberte. Nous degagerons la notion de modes d'oscillations et de coordonnees normales, et nous discuterons la notion de batte- ments ainsi que les echanges d'energie entre les oscillateurs. Cette m^emeetude, a 1 ou 2 oscillateurs couples, sera reprise dans le 3eme chapitre en regime force, c'est-a-dire en presence d'une force exterieure. Nous mettrons en evidence les regimes dits transitoires et permanents de ces systemes forces, tandis que l'analyse de la puissance fournie par la force exterieure aux oscillateurs nous conduira a la notion de resonance. Enn, en partant d'une analyse des modes de ces oscillateurs couples, nous introduirons les notions de frequences de coupure, de bande passante et plus generalement de ltrage 2. Enn, en augmentant le nombre d'oscillateurs couples et donc le nombre de degres de libertes, nous montrerons dans le 4eme chapitre, par un passage a la limite continue, que l'on peut retrouver le comportement ondulatoire des systemes decrits par une equation aux derivees partielles du type des cordes vibrantes :2u(x;t)@t
2=v2@2u(x;t)@x
2 ouu(x;t) est la deformation du systeme a la positionx, a l'instanttet ouvest la vitesse de propagation de l'onde de deformation. Ce passage a la limite con- duit aussi bien aux ondes longitudinales telles que celles rencontrees en acoustique, qu'aux ondes transversales telles que celles intervenant en electromagnetisme ou en dynamique des structures. En suivant cette approche, on passera progressivement de systemes discrets ou la masse est localisee dans l'espace (typiquement dans les masses accrochees aux2 Lorsque la force exterieure est periodique, nous montrerons que le comportement asymptotique d'un oscillateur lineaire, c'est-a-dire son comportement aux temps longs, est lui-m^eme periodique de m^eme periode. Il n'en va plus de m^eme lorsque l'oscillateur est non-lineaire. Par exemple, dans le cas general du pendule pour lequel l'equation dierentielle s'ecrit sous la forme : (t) =sin(t)1Q _(t) +Asin!tle couplage de la non-linearite et du forcage peut conduire a des solutions asymptotiques periodiques
de periodes,T= 2=!;2T;4T;, voire a une evolution chaotique. L'etude des systemes dierentiels non lineaires (on parle maintenant de theorie des systemes dynamiques ou theorie du chaos) constitue un champ disciplinaire immense, considerablement plus riche et complexe que celui des systemes lineaires, mais dont on rencontre egalement des illustrations dans tous les domaines de la physique, voire des sciences. 6 x 1(t)x 1(t)x 2(t)x 1(t)x 2(t)x3(t)u(x;t)Figure 1.4: Exemple de passage a la limite continue par augmentation du nom-
bre de degres de liberte (cas des oscillations transversales de masses couplees elastiquement). ressorts ou placees a l'extremite des pendules), a des systemes continus ou la masse est repartie contin^ument dans l'espace (par exemple le long d'une corde). Ce cours devrait donc vous permettre d'utiliser et d'approfondir les notions de mecanique acquises en L1 et au 1er semestre de L3, a etablir un lien avec le cours d'ondes suivi en L2, le tout en utilisant vos connaissances mathematiques (en par- ticulier sur les equations dierentielles et l'algebre lineaire).Le plan du cours sera le suivant :
Chapitre 1 : Introduction
Chapitre 2 : Oscillations libres des systemes a 1 et 2 degres de liberte. 7 Chapitre 3 : Oscillations forcees des systemes a 1 et 2 degres de liberte. Chapitre 4 : Oscillations des systemes andegres de liberte et limite continue.Bibliographie selective
L'ouvrage le plus proche du cours est probablement : Le cours de physique de Berkeley, Ed. Armand Colin {Volume 1 : Mecanique (chapitres 5, 6, 7) {Volume 3 : Ondes (chapitres 1, 2, 3, 4) L'ouvrage suivant est d'un niveau plus eleve et plus synthetique : Mecanique, L. Landau et E. Lifchitz, Ed. Mir (chapitre 5) Celui-ci contient des rappels de cours et de nombreux exercices corriges de niveau variable :Mechanical vibrations, William Seto, Ed. Schaum
Un cours complet de mecanique :
Mecanique, fondements et applications, J. Ph. Perez, Ed. Dunod (chapitres10, 11, 27)
Enn, pour ceux d'entre vous qui voudraient se faire une idee d'un prolonge- ment de ce cours vers les oscillateurs non-lineaires, on peut citer : L'ordre dans le chaos, P. Berger, Y. Pomeau, C. Vidal, Ed. Hermann The chaotic pendulum, M. Gitterman, Ed. World Scientic The noisy oscillator, M. Gitterman, Ed. World Scientic 8Chapter 2
Oscillations libres a 1 et 2 degres
de liberte2.1 Oscillations libres a 1 degre de liberte
On dit qu'un systeme esta 1 degre de libertelorsqu'une seule variable est necessaire pour decrire le mouvement.2.1.1 Exemples
Sans ^etre exhaustif, on peut citer comme exemples d'oscillations a 1 degre de liberte les oscillations longitudinales ou transversales d'une masse accrochee ressortk mx(t)mx(t)les oscillations des pendules pesants ou des pendules de torsion.m` (t)(t)C 1 les oscillations de charges ou de courant dans les circuits electriquesLi(t)R C Mis a part le circuit RLC qui constitue intrinsequement un exemple d'oscillateur lineaire puisqu'il n'est constitue que de composants lineaires (resistance, inductance et capacite), les oscillateurs mecaniques peuvent operer en regime lineaire ou non- lineaire, selon que l'ecart a la position d'equilibre est faible ou important. Dans les dierents exemples presentes ci-dessus, la variable decrivant le mouve- ment au cours du temps est soit une elongationx(t), soit un angle(t), soit une charge electriqueq(t) ...2.1.2 Equation du mouvement
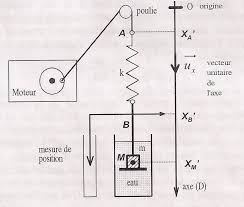
Dans la mesure ou on se restreint a l'etude des oscillateurs lineaires, la force de rappel s'exercant sur le systeme est proportionnelle a la variable decrivant le mouvement. Dans les exemples presentes ci-dessus, ces forces s'ecriront sous la forme :kx(t) et mg(t) dans le cas du ressort et du pendule, le couple de rappel du l de torsion s'ecritC(t), la tension aux bornes de la capacite estq(t)=C, etc. Le principe fondamental de la dynamique applique au systeme masse-ressort vertical par exemple (massem, constante de rappel du ressortkde longueur a vide0), s'ecrit dans un repere lie au support, sous la forme suivante (schema de droite):
mz(t) =k(z(t)`0) +mg A l'equilibre (schema du milieu), le poids compense la force de rappel du ressort :0 =k(`eq`0) +mg
En faisant la dierence de ces 2 equations, on trouve aussit^ot : mz(t) =k(z(t)`eq) Il est commode d'introduire la position par rapport a l'equilibre,x(t) =z(t)`eq qui, puisque x(t) = z(t), conduit aussit^ot a l'equation : mx(t) =kx(t) 2 Cette situation est generique quel que soit le probleme. On gagne souvent en sim- plicite en exprimant les deplacements par rapport a la position d'equilibre. C'est ce que nous ferons d'une facon systematique dans la suite de ce cours.k` 0` eqmz(t)x(t) =z(t)`eqOn peut se placer dans une situation un peu plus generale en introduisant une eventuelle force de frottement uide 1: mx(t) =kx(t)_x(t) ou _x(t) est la vitesse relative de la masse par rapport au uide et ouest le coecient de frottement. En introduisant les variables 2=met!20k=m, cette equation s'ecrit encore sous la forme : x+ 2_x+!20x= 0 (2.1) Cette equation dierentielle est l'equation caracteristique qui decrit le mouvement des oscillateurs libres a 1 degre de liberte.Remarques
1. Il appara ^tcla irement apartir de cette equationque les deux param etrescar- acterisant l'oscillateur, a savoir,et!0, sont homogenes a l'inverse d'un temps. 2. Une equationpr esentantla m ^emestructure d ecritles autres oscillateurs a partir des variables(t);q(t); 3. On parle d'oscillateur amorti ou dissipatiflorsque6= 0, d'oscillateur non amorti ou non dissipatif lorsque= 0.Application
Determiner!20pour les dierents oscillateurs presentes plus haut.1 Ce regime n'est qu'une approximation. Dans certains cas, on doit recourir a une force de frottement visqueux non-lineaire de typej_xj_x, voire a des frottements solides du type donne par la loi de Coulomb. 32.1.3 Solutions des equations du mouvement
L'equation (2.1) est une equation dierentielle lineaire, du 2nd ordre, homogene et a coecients constants. Rappelons que les solutions d'une telle equation peuvent ^etre recherchees sous la formex(t) =Aertce qui, apres substitution dans l'equation conduit a l'annulation du polyn^ome caracteristique :P(r) =r2+ 2r+!20= 0
dont les 2 racines sont : r 1;2=q 2!20Regime non amorti:= 0
Dans ce cas, les 2 racines sont imaginaires pures et conjuguees :r1;2=i!0. La solution generale de (2.1) s'ecrit donc sous la forme : x(t) =C1e+i!0t+C2ei!0t ouC2etC2sont 2 constantes complexes dependant des conditions initiales.x(t) devant ^etre reelle, il est preferable d'ecrire la solution sous les formes equivalentes suivantes : x(t) =B1cos(!0t) +B2sin(!0t) oux(t) =acos(!0t+') Dans cette derniere expressionaest l'amplitude du mouvement et'la phase au temps origine. Le mouvement est donc periodique, de periodeT02=!0, sans attenuation d'amplitude.tx(t)a+aT 0=2!0Regimes amorti et sur-amorti:6=!0
Dans ce cas, la solution generale peut s'ecrire sous la forme : x(t) =C1er1t+C2er2t our1;2=p 2!20.Deux cas sont a distinguer :
4 si < !0, les 2 racinesr1;2sont imaginaires conjuguees :r1;2=i!ou !p!202. la solution peut donc s'ecrire sous la forme :
x(t) =aetcos(!t+') Il s'agit a nouveau d'un mouvement periodique (on dit parfois pseudo-periodique), de periodeT= 2=! > T0, d'amplitude decroissante avec le temps car- acteristique1. L'oscillateur est qualied'amorti.tx(t)a+aT=2! si > !0, les 2 racinesr1;2sont reelles et negatives. La solution est une combinaison de 2 exponentielles avec 2 temps caracteristiques dierentsr11;2: x(t) =et C 1ep2!20t+C2e+p
2!20t Le mouvement est sans oscillation et le regime est ditsur-amortiouaperiodique.Application
Determiner le temps caracteristique dominant lorsque!0, et en deduire le comportement aux temps longs ainsi que l'equation dierentielle veriee par l'oscillateur dans cette situation.Regime critique:=!0
Dans, ce cas,r1;2=est racine double du polyn^ome caracteristique. Le deplacement verie donc l'equation : x(t) = (C1+C2t)et Le mouvement est non oscillant avec 1 seul temps caracteristique1. Ce regime, egalement aperiodique, est ditcritique. Globalement, on pourra retenir que le cas particulier=!0separe les cas des reponses periodiques ( < !0) et non-periodiques (!0) des oscillateurs lineaires.quotesdbs_dbs12.pdfusesText_18[PDF] etude d'un système masse-ressort corrigé
[PDF] oscillateur amorti par frottement solide
[PDF] la place annie ernaux texte intégral
[PDF] système masse ressort horizontal
[PDF] oscillateur harmonique ressort horizontal
[PDF] système squelettique fonction
[PDF] système osseux définition
[PDF] système squelettique humain
[PDF] programme sciences école primaire
[PDF] à la place de synonyme
[PDF] à la place en anglais
[PDF] "à la place de" "au lieu de"
[PDF] système verbal définition
[PDF] outils prevention tabac
